Keywords

1 Introduction

Evolutionary Computation (EC) is primarily concerned with the design and analysis of robust search algorithms, called Evolutionary Algorithms (EAs), modelled after natural evolution. Besides robustness, EAs stochastically exhibit complex population dynamics, which renders them difficult to comprehend and be harnessed. Empirical [5], theoretical [6] and visual [7] analyses are the means by which research efforts are being undertaken to comprehend the dynamics and behavior of EAs. Few research works have attempted to represent and visualize interactions within EAs as graphs. However, these works have merely proposed several graph-theoretic measures to analyze EA dynamics, without appropriate validation.

The first research on graph-based analysis of EAs was presented in [12]. Ivan Zelinka et al. [15] modelled Differential Evolution (DE) and Self-Organizing Migrating Algorithm (SOMA) as graphs and this idea was extended, with little or no modification, to Differential Evolution (DE) [2, 8, 9] and Particle Swarm Optimization (PSO) [8]. Various properties of graph that could provide insights into EA dynamics were suggested in [2, 8], and are summarized in Table 1. In all these works, several graph-theoretic measures were mapped to some EA dynamics/property, but lacked appropriate validation of these mappings.

Table 1. Graph measures and possible insights about EAs [2, 8]
Full size table

This paper presents critical analysis of a prominent graph model, proposed in [15], and applied in [2, 8, 9, 14]. The in-depth analysis involves modelling the interactions within DE/rand/1/bin and DE/best/1/bin algorithms as graphs, while solving CEC2005 benchmark functions [10]. Subsequent to modelling, the graph-theoretic measures- degree centrality, clustering coefficient, betweenness centrality and closeness centrality- are employed to investigate the potential of the graph model in understanding EA dynamics. The remaining sections of this paper are structured as follows: Sect. 2 outlines the prominent graph model from the literature, in the context of DE algorithm. Section 3 explains the experimental design. Section 4 presents the simulation results and analysis. Section 5 concludes this work with suggestions on future studies.

2 Graph Model for DE

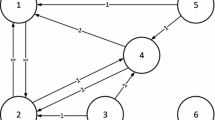
Differential Evolution is a simple, robust evolutionary algorithm, primarily applied for continuous optimization problems. For each target vector in the DE population, three random solutions, in the population, interact to create a mutant vector, which in turn undergoes crossover with the corresponding target vector to create a trial vector. In graph creation, the identified graph model focuses on these individuals, except the transitory mutant vector. The graph creation has been explained in Algorithm 1 (for DE/rand/1/bin) and Fig. 1 shows an example for the same.

Since the number of vertices is always the population size (N), a new trial vector in the next generation gets represented by the same vertex that used to represent its corresponding target vector in a previous generation. Thus, vertices in the graph cannot be related directly to individuals, instead can be interpreted as place holders, for individuals in newer evolving populations. The graph model, described in this section, attempts to effectively capture the interactions within a typical DE algorithm. However the potential of this graph model has not been amply demonstrated in respective literature.

figure a
Fig. 1.
figure 1

An example for graph creation during DE run with the considered graph model

Full size image

3 Experimental Design

The critical evaluation of the graph model, outlined in the previous section, calls for a rigorous, systematic empirical analysis. Towards this, DE/rand/1/bin and DE/best/1/bin algorithms were used to optimize 25 functions from the CEC2005 benchmark suite [10]. The following parameters were used during the simulations: N = 50, D = 10, F = 0.4, Cr = 0.5 and Maxgen = 5000. 30 runs were executed, for each function in the benchmark suite, using both the algorithms. The graph creation algorithm, described in Algorithm 1, was used to create directed weighted graphs, for each run-function-algorithm in the benchmark suite. The following four prominent graph theoretic measures (refer Table 1), proposed in the literature, have been employed for graph analysis.

  1. 1.

    Degree Centrality: Since the average indegree of vertices in a graph is equal to the average outdegree, we limit our focus to the indegree of vertices. Indegree of a vertex in a directed weighted graph is the sum of edge weights coming into that vertex [13].

    $$\begin{aligned} indeg(u)=\sum _{v\in V-\{u\}}w_{vu} \end{aligned}$$
    (1)

    where V is the set of vertices, and \(w_{vu}\) is the weight of the edge vu representing the number of times the individual at vertex v helped to improve the individual at vertex u.

  2. 2.

    Clustering Coefficient: The local clustering coefficient of a vertex, in a weighted directed graph, is computed using the following equation [3]:

    $$\begin{aligned} cc(i)=\frac{1/2\sum _{j}\sum _{k}{({w_{ij}^{\frac{1}{3}}+w_{ji}^{\frac{1}{3}}})({w_{ik}^{\frac{1}{3}}+w_{ki}^{\frac{1}{3}}})({w_{jk}^{\frac{1}{3}}+w_{kj}^{\frac{1}{3}}})}}{{{{d_i}^{tot}}({{d_i}^{tot}}-1)}-(2\times {{d_i}^{bidir}})} \end{aligned}$$
    (2)

    where, i, j and k are three distinct vertices, \({d_i}^{tot}\) is the total degree of vertex i, \({d_i}^{bidir}\) is the number of bidirectional edges at vertex i.

  3. 3.

    Betweenness Centrality: The betweenness centrality of a vertex, in a weighted directed graph, is calculated by the following equation [4]:

    $$\begin{aligned} betw(i)=(\sum {\frac{\sigma _{uv}^i}{\sigma _{uv}}})\times {\frac{1}{(N-1)(N-2)}} \end{aligned}$$
    (3)

    where, u, v and i are three distinct vertices, \({\sigma _{uv}^i}\) is the count of shortest paths between u and v through i, \({\sigma _{uv}}\) is the count of shortest paths between u and v, and N is the number of vertices in the graph.

  4. 4.

    Closeness Centrality: The closeness centrality of a vertex, in a weighted directed graph, is computed by the following equation [1]:

    $$\begin{aligned} close(i)={\frac{\left| R(i)\right| }{N-1}}\times {\frac{\left| R(i)\right| }{\sum \limits _{u \in R(i)}{d(i,u)}}} \end{aligned}$$
    (4)

    where, R(i) is the set of vertices reachable from vertex i, N is the number of vertices in the graph, \({\frac{\left| R(i)\right| }{N-1}}\) is the normalization for closeness centrality, and d(i, u) is the shortest distance from i to u.

4 Simulation Results and Analysis

The four identified graph theoretic measures were computed, for every graph generated per run of DE/best/1/bin and DE/rand/1/bin, while solving CEC2005 functions. The results were plotted across the number of generations. Based on these plotted results, the analysis, are presented below, for each of the four graph measures. In all the following figures, showing the plots for 30 runs, red color solid lines represent convergence, cyan color dashed lines represent premature convergence and magenta color dashed-dotted lines represent stagnation. Due to space limitations, the plots in this section have been organized to show few patterns of growth for each graph measure. It is also worth pointing out that though each pattern of growth is shown for only one function, the remaining functions also displayed patterns similar to the ones presented here.

4.1 Degree Centrality

The degree centrality analysis has been proposed, in the literature, to observe the premature convergence or stagnation, in an evolutionary run (refer Table 1). Figure 2 shows runs of F15 with DE/rand/1/bin, which resulted in convergence and premature convergence. Figure 3 shows runs of F25, which resulted in premature convergence and stagnation. We can see that the state of the DE run (whether it is convergence/premature convergence/stagnation) is not completely distinguishable from the figures. As it happens with a typical EA run, initial generations are marked by faster fitness improvements followed by a long slower improvement phase. As long as there are fitness improvements in the population, edges are formed between vertices contributing to indegree growth. The indegree growth stops if the population gets into convergence/premature convergence as a single (global/local) solution dominates and takes over the population making it to lose diversity in subsequent generations. The indegree growth may also stop if there is stagnation where the population is still diverse but unable to evolve further. Figure 4 shows the average fitness (of single run) plotted against indegree growth, for the function F15. A quick comparison reveals that degree centrality based graph analysis do not offer advantage over average fitness and observing the latter in few past generations is suffice between the two to sense premature convergence/stagnation.

Fig. 2.
figure 2

Average indegree for 30 runs of F15 for DE/rand/1/bin

Full size image
Fig. 3.
figure 3

Average indegree for 30 runs of F25 for DE/rand/1/bin

Full size image
Fig. 4.
figure 4

Average indegree and Average fitness of F15 for DE/rand/1/bin

Full size image

4.2 Clustering Coefficient

It is suggested in the literature (refer Table 1) that clustering coefficient shall be used to get insights about population diversity. Figure 5 shows the average weighted clustering coefficient for 30 runs of F14 plotted against generations for DE/best/1/bin. As the population evolves over generations, the edge weights in the neighborhood of nodes increases, thereby increasing the average weighted clustering coefficient. The successful evolution of a population also correlates with gradual loss of its diversity. This inverse relationship can be observed in Fig. 6 (diversity calculated using P-measure [11]). The population diversity, when measured directly and used effectively, is potential enough to serve as an effective means to understand the dynamics of an EA run.

Fig. 5.
figure 5

Average weighted clustering coefficient of F14 for DE/best/1/bin

Full size image
Fig. 6.
figure 6

Average weighted clustering coefficient and population diversity of F14 for DE/best/1/bin

Full size image
Fig. 7.
figure 7

Average betweenness centrality for 30 runs of F8 for DE/rand/1/bin

Full size image
Fig. 8.
figure 8

Average betweenness centrality for 30 runs of F15 for DE/rand/1/bin

Full size image

4.3 Betweenness Centrality

It has been commented in the literature (refer Table 1) that the node having the highest betweenness incidentally has the best fitness. We observed that quite often there was no such correlation. In case of the underlying graph model a node is more like a place holder! The increased contribution of a node, towards the improvement of another node, is captured by increasing the weight of the edge between them. On the contrary, the betweenness centrality, which calculates shortest path, favors the nodes with lesser edge weights. The undertaken graph model does not address this conflict. The above observation extends to the closeness centrality measure too. Since this work is intended to analyze the graph model as is, we proceeded with betweenness centrality and closeness centrality calculations. Figures 7 and 8 show the average betweenness centrality plotted against generations for F8 and F15 solved by DE/rand/1/bin. At the beginning, edges are added between nodes leading to increased betweenness values. When the graph becomes more and more complete during evolution, the betweenness centrality reduces and then stabilizes.

4.4 Closeness Centrality

Closeness centrality, in literature, has been proposed as a measure of rate of distribution of information in the population (refer Table 1). Figure 9 shows as an example, the cumulative closeness centrality for each node in the graph, at the end of 5000 generations for F1 solved by DE/best/1/bin. It can be observed from the figures that there are nodes which have displayed very active contribution in evolution while there are also quite a few nodes which have not contributed much in the improvement of other nodes. The concept of nodes as place holder makes this observation not so worthwhile. The behavior of cumulative closeness of all the N nodes over 5000 generations is shown in Fig. 10. Being cumulative, it just increases over generations.

Fig. 9.
figure 9

Cumulative closeness of each node at the end of one run of F1 for DE/best/1/bin

Full size image
Fig. 10.
figure 10

Cumulative closeness of all nodes over generations during one run of F1 for DE/best/1/bin

Full size image

5 Conclusion

This paper presented a critical analysis of an existing prominent graph model of EAs. Graph theoretic analysis of EAs could be used to verify the empirical and theoretical analyses’ about EAs and also to complement them in understanding those algorithms. This also offers the prospect of controlling the dynamics of EAs, so as to improve the efficacy of EAs leading to better and robust designs. However the potential of graph based analysis of EAs largely rests with the underlying graph model. The graph model, analyzed in this paper, represents N individuals in the population as N vertices in the graph. Since the number of vertices remain the same, even as the population evolves, the vertices represent the descendants of each individual in the initial population. Nodes in the graph serve as place holders for individuals. While this modelling abstraction attempts to capture interactions within DE, in a cumulative sense, it certainly limits analysis, because apart from interactions, the evolution of population is also a critical factor in understanding EAs.

In case of degree centrality, the analysis did seem to provide only a coarse insight about the convergence of EA runs. Statistical analysis of DE runs could very well provide better insights into convergence. Since the clustering coefficient of the modelled graph displayed an inverse relationship with population diversity, the latter could serve as an effective means to understand the dynamics of an EA run. The betweenness centrality and closeness centrality measures did not seem to provide any valuable insights about DE runs. It is felt that the inability of prominent graph properties to provide any worthwhile insight is by virtue of the adopted graph model, whose potential is largely determined by its very modelling process. Since graph based analysis of EAs is a prospective method of analysis, complementing empirical and theoretical analyses, designing effective graph model of EAs are perceived to be the major attention for future investigations.