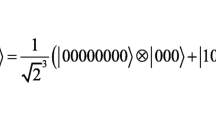Keywords

1 Introduction

Quantum image processing (QIP) has been focused due to its ability to storing N bits classical information in only log 2N quantum bits. The important properties of QIP such as entanglement, parallelism and exponential increase of quantum storage capacity make it unique [1]. In fact QIP is three-step technique-first step, representation of the classical digital image in a quantum image. The second step, quantum image is processed using quantum computation technologies and finally, images are extracted from processed quantum images. There are two broad groups of QIP - quantum inspired image processing and classically inspired quantum image processing [2,3,4]. In two groups, the primary task of QIP starts with the proper representation of conventional images in terms of quantum bits. In this direction many techniques such as quantum image model based on Qubit Lattice [5, 6], flexible representation of quantum image (FRQI) [7], novel enhanced quantum representation (NEQR) [8], Quantum log-polar images [9], normal arbitrary quantum superposition state [10] are already reported. Different QIP techniques such as quantum image scrambling [11,12,13], quantum image geometric transformation [14], and quantum image scaling [15], have been developed on the basis of quantum image representation (QIR) model.

The main three drawbacks which makes constraint in the application such as medical, pattern recognition, image features extraction, inaccurate retrieve of an original classical image, restricted quantum operations performed in QIP and limited to the representation of a large number of color using angle parameter of qubits. In spite of these drawbacks, Fan et al. [16, 17] have reported quantum image edge extraction based Sobel operator and Laplacian operators. Till the main issues in image edge extraction are high computational complexity and loss of edge information in a certain direction [14]. In comparison to classical image edge extraction, QIP can process all pixels of an image simultaneously by using unique superposition and entanglement properties of quantum mechanics. Both FRQI and NEQR have already been used for quantum image extraction [16, 18, 17]. In both cases, time complexity decreases exponentially but these schemes provide misclassification of noise pixels as edge points. Although Fan et al. [17] has proposed an enhanced quantum edge extraction scheme based on Laplacian filtering with NEQR for detection of image edge by smoothing. But till problem lies in accurate edge detection in all the directions.

Here we have proposed quantum image edge detection using four directional Sobel operator for gradient estimation to obtain more actual edge information. We use NEQR [8] method for QIR because it is extremely similar to classical image representation. NEQR utilizes the quantum states of superposition to store all the pixel of the image, therefore all the pixels data can be process simultaneously. The Mathematical modules of a proposed scheme has been developed to obtain an accuracy of edge extraction.

2 Related Work

The novel enhanced quantum representation (NEQR) [8]. In NEQR model [18], two entangled qubit sequences are used to store the grayscale value and positional information of all the pixels of image in superposition states [18]. Quantum image representation for 2n × 2n image is expressed as

$$ \left| {I > } \right. = \frac{1}{{2^{n} }}\sum\nolimits_{Y = 0}^{{2^{n} - 1}} {\sum\nolimits_{X = 0}^{{2^{n} - 1}} {\left| {C_{YX} > \left| {Y > } \right.} \right.\left| {X > } \right.} } = \frac{1}{{2^{n} }}\sum\nolimits_{YX = 0}^{{2^{2n} - 1}} {{}_{k = 0}^{q - 1} \otimes \left| {C_{YX}^{k} > } \right. \otimes \left| {YX > } \right.} $$
(1)

where grayscale value of the pixel coordinate (Y, X),

$$ C_{YX} = C_{YX}^{q - 1} C_{YX}^{q - 2} \ldots \ldots C_{YX}^{1} C_{YX}^{0} ; C_{YX}^{k} \in \left\{ {0,1} \right\};\;C_{YX} \in \left[ {0,2^{q} - 1} \right] $$

The accurate classical image can be retrieved from NEQR method.

2.1 Classical Sobel Edge Detection Algorithm

Sobel operator is a discrete differential operator. It has two sets of 3 × 3 mask shown in Fig. 1(b) and (c) and mainly used for edge detection. If GH and GV represents the image gradient value of the original image for horizontal and vertical direction then the calculation of GH & GV is defined as

Fig. 1.
figure 1

(a) The 3 \( \times \) 3 neighborhood templates, (b) and (c) are two Sobel masks.

Full size image
$$ \begin{aligned} G^{V} \,{ = } & \,S\left( {Y - 1,\;X + 1} \right) + 2S\left( {Y,\;X + 1} \right) + S\left( {Y + 1,\;X + 1} \right) - S\left( {Y - 1,\;X - 1} \right) - 2S(Y,\;X \\ & - \,1) - S\left( {Y + 1,\;X - 1} \right) \\ \end{aligned} $$
(2)
$$ \begin{aligned} G^{H} \, = & \,S\left( {Y + 1,\;X - 1} \right) + 2S\left( {Y + 1,\;X} \right) + S\left( {Y + 1,\;X + 1} \right) - S\left( {Y - 1,\;X - 1} \right) - \,2S(Y - 1, \\ & X) - S\left( {Y - 1,\;X + 1} \right) \\ \end{aligned} $$
(3)

The total gradient for each pixel is as follows

$$ G \cong \left| {G^{V} } \right| + \left| {G^{H} } \right| $$
(4)

If G ≥ T (Threshold), the pixel will be the part of edge points.

2.2 Four Directional Sobel Edge Detection

Classical Sobel operator is limited to only vertical and horizontal direction. The performance of this operator can further be increased if the direction template are changed into four directions for gradient estimation (i.e. vertical, horizontal, 45° and 135° direction) is shown in Fig. 2(a) and (b). If G1d and G2d represents the gradient value of an image through 45° and 135° directions then gradient estimation can be expressed as follows

Fig. 2.
figure 2

(a) 45° direction. (b) 135° direction.

Full size image
$$ G^{D1} = S\left( {Y,\;X + 1} \right) + 2S\left( {Y + 1,\;X + 1} \right) + S\left( {Y + 1,\;X} \right) - S(Y - 1,\;X) - 2S(Y - 1,\;X - 1) - S\left( {Y,\;X - 1} \right) $$
(5)
$$ G^{D2} = S\left( {Y - 1,\;X} \right) + 2S\left( {Y - 1,\;X + 1} \right) + S\left( {Y,\;X + 1} \right) - S\left( {Y,\;X - 1} \right) - 2S(Y + 1,\;X - 1) - S\left( {Y + 1,\;X} \right) $$
(6)

Total gradient of each pixel is calculated as follows

$$ G \cong \left| {G^{V} } \right| + \left| {G^{H} } \right| + \left| {G^{D1} } \right| + \left| {G^{D2} } \right| $$
(7)

3 Quantum Image Edge Detection Based on Four Directional Sobel Operator

3.1 Algorithm for Edge Detection

  • I. Prepare the quantum image \( \left| I \right\rangle \) from the original digital image. Here we use NEQR model for QIR.

  • II. Use cyclic shift transformations to obtain the shifted quantum image set.

  • III. Calculate the every pixel gradient for all the four directions (i.e. vertical, horizontal, 45° and 135°) using Sobel mask and record them as \( \left| {G > } \right.. \)

  • IV. Compare all the gradients (i.e.\( \left| {G^{V} > } \right.,\left| {G^{H} > } \right.,\left| {G^{D1} > } \right. \) & \( \left| {G^{D2} > } \right. \)) with a threshold value \( \left| {T_{H} > } \right. \) through four quantum comparators. If each of the gradient value is less than \( \left| {T_{H} > } \right. \) then it is defined as a non-edge point, otherwise it is an edge point.

Different steps of the algorithm can be describe as follows:

  • Step-I: The original digital image is represented into a quantum image using NEQR method and (2n + q) qubits are needed to store this quantum image. In order to store the eight pixels of a 3 × 3 neighborhood window, 8 extra qubits are required and these qubits are the tensor product with \( \left| I \right\rangle \) i.e.

    $$ \begin{aligned} \left| {0 > } \right.^{{ \otimes^{8q} }} \otimes \left| {I > } \right.\; = & \;\frac{1}{{2^{n} }}\sum\nolimits_{Y = 0}^{{2^{n} - 1}} {\sum\nolimits_{X = 0}^{{2^{n} - 1}} {\left| {0 > } \right.^{{ \otimes^{8q} }} \left| {C_{YX} > } \right.\left| {Y > } \right.\left| {X > } \right.} } \\ = & \;\frac{1}{{2^{n} }}\sum\nolimits_{Y = 0}^{{2^{n} - 1}} {\sum\nolimits_{X = 0}^{{2^{n} - 1}} {\left| {0 > } \right.^{{ \otimes^{q} }} \ldots \ldots \left| {0 > } \right.^{{ \otimes^{q} }} \left| {C_{YX} > } \right.\left| {Y > } \right.\left| {X > } \right.} } \\ \end{aligned} $$
    (8)

  • Step-II: The main operation of this stage is X-shift and Y-shift transformation of pixels. Any neighborhood eight pixels of \( \left| {I > } \right. \) are stored and encoded in the quantum states as follows

    $$ \begin{aligned} & \frac{1}{{2^{n} }}\sum\nolimits_{Y = 0}^{{2^{n} - 1}} {\sum\nolimits_{X = 0}^{{2^{n} - 1}} {\left| {C_{Y - 1,X} > } \right. \otimes \left| {C_{Y - 1,X + 1} > } \right. \otimes \left| {C_{Y,X + 1} > } \right. \otimes \left| {C_{Y + 1,X + 1} > } \right. \otimes \left| {C_{Y + 1,X} > } \right. \otimes } } \\ & \left| {C_{Y + 1,X - 1} > } \right. \otimes \left| {C_{Y,X - 1} > } \right. \otimes \left| {C_{Y - 1,X - 1} > } \right. \otimes \left| {C_{Y,X} > } \right.\left| {Y > } \right.\left| {X > } \right. \\ \end{aligned} $$
    (9)

  • Step-III: Different quantum arithmetic operations are used to calculate the gradient of every pixel. The output quantum states \( \left| {G > } \right. \) for intensity gradient can be expressed as follows

    $$ \left| {G > } \right. = \frac{1}{{2^{n} }}\sum\nolimits_{Y = 0}^{{2^{n} - 1}} {\sum\nolimits_{X = 0}^{{2^{n} - 1}} {\left| {G_{Y,X}^{V} > } \right.\left| {G_{Y,X}^{H} > } \right.\left| {G_{Y,X}^{D1} > } \right.\left| {G_{Y,X}^{D2} > } \right.\left| {Y > } \right.\left| {X > } \right.} } $$
    (10)

  • The quantum state \( \left| {G > } \right. \) can be encoded as follows

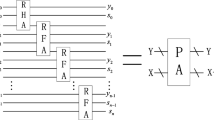
    $$ \left| {0 > } \right. \otimes \left| {G > } \right. = \frac{1}{{2^{n} }}\sum\nolimits_{Y = 0}^{{2^{n} - 1}} {\sum\nolimits_{X = 0}^{{2^{n} - 1}} {\left| {0 > } \right.\left| {G_{Y,X}^{V} > } \right.\left| {G_{Y,X}^{H} > } \right.\left| {G_{Y,X}^{D1} > } \right.\left| {G_{Y,X}^{D2} > } \right.\left| {Y > } \right.\left| {X > } \right.} } $$
    (11)

    The quantum circuit realization of gradient \( \left| {G > } \right. \) is shown in Figs. 3(a) and (b).

    Fig. 3.
    figure 3

    (a) Circuit realization of quantum module for calculating the gradient of a quantum image through vertical and horizontal direction. (b) Circuit realization of quantum module for calculating the total gradient of each pixel of a quantum image. (c) Circuit realization of quantum module for final states of our proposed algorithm and stored in a quantum states \( \left| {D_{E} > } \right. \).

    Full size image

  • Step-IV: In order to detect the edge points of \( \left| {I > } \right. \), four quantum comparator are used to compare the intensity gradients of every pixel in the four directions with a given threshold \( \left| {T_{H} > } \right. \). All the gradients of \( \left| {G_{Y,X}^{V} > } \right.,\left| {G_{Y,X}^{H} > } \right.,\left| {G_{Y,X}^{D1} > } \right. \) & \( \left| {G_{Y,X}^{D2} > } \right. \) greater than equal to \( \left| {T_{H} > } \right. \) classified as an edge point. The final state for quantum edge extraction can be represented as follows

    $$ \left| {D_{E} > } \right. = \frac{1}{{2^{n} }}\sum\nolimits_{Y = 0}^{{2^{n} - 1}} {\sum\nolimits_{X = 0}^{{2^{n} - 1}} {\left| {D_{Y,X} > } \right.\left| {Y > } \right.\left| {X > } \right., D_{Y,X} \in \left\{ {0,1} \right\}} } $$
    (12)

  • where \( D_{Y,X} \) = 0, means no edge point and \( D_{Y,X} \) = 1, means edge point. Circuit realization of quantum states \( \left| {D_{E} > } \right. \) is shown in Fig. 3(c). During the circuit realization, we ignored all the other garbage qubits of the output.

3.2 Quantum Circuit Realization for Edge Detection

The various quantum operations are required for image edge extraction. Here we use quantum image cyclic shift transformations [14, 19], parallel controlled-NOT operations, Quantum operation of multiplied by powers of 2, quantum ripple-carry adder (QRCA) [20], quantum absolute value (QAV) module [21, 22] and quantum comparator (QC) [23] to realize the quantum circuit for edge detection algorithm.

4 Results and Discussion

Computational complexity is an important factor for comparison of different image edge detection techniques. The circuit complexity of our scheme is ~O(n2 + q2), which result into exponential speed up compare to all the classical image edge extraction schemes and existing Sobel quantum image edge extraction method [6, 16, 18]. We have prepared a performance comparison between our proposed algorithm and other existing Sobel edge detection algorithms for a 2n × 2n size of digital image as shown in Table 1. However computational complexity of quantum image preparation is not consider in QIP. In order to test our proposed algorithm, all the experiments are simulated in MATLAB R2018a environment on a classical computer Intel (R) Core™i58300HCPU 2.30 GHz, 8.00 GB RAM. Three common original test images such as Lena, peppers and Cameraman [24] were chosen for edge extraction simulation with same threshold value (TH = 127) as shown in Fig. 4a. Our proposed algorithm can extract more edge information than that extracted using classical Sobel algorithm (Fig. 4b) [25] and quantum Sobel edge extraction (Fig. 4c) [16]. This is due to bit to bit parallel processing and gradient estimation in all directions. However, there is less probability of missing of actual information and detecting false edge information in our proposed algorithm as estimation in all four directions. The simulation result also shows that the image contour is more brightly obtained in our proposed edge extracted images (Fig. 4d) due to absolute intensity value of the pixels. So the simulation result of our proposed quantum method demonstrate accurate edge detection with smooth edge in all four directions.

Table 1. Performance comparison of an image with a size of 2n × 2n.
Full size table
Fig. 4.
figure 4

Test images and their edge extraction (a) original image of Lena, Pepper and Cameraman [24]. (b) Classical Sobel edge extracted images. (c) Quantum Sobel edge extracted images. (d) Result images of our proposed algorithm.

Full size image

5 Conclusion

Due to bit-level parallelism, the edge extracted process of QIP is much richer than the classical image processing (CIP). Compare to classical Sobel algorithm, it extracts more information and edges of the image is more specific. However, real time problem, discontinuity, roughness and other defects of Sobel edge detection algorithms can be reduced using our proposed algorithm. The proposed algorithm would be a clinically feasible practice for edge detection of medical images in future.