Keywords

1 Introduction

Magnetic resonance imaging (MRI) offers several advantages, like, good contrasts for soft-tissue imaging, non-invasiveness, no ionizing radiations, etc. compared to other well known medical imaging modalities, like, X-ray, ultrasound, and computed tomography (CT). However, MRI suffers from two major problems, long scan time and acoustic noise due to gradient variations. Although, multi-channel or parallel MRI (pMRI) significantly reduces the acquisition time, yet it requires 20 to 40 min for imaging depending on the field-of-view (FoV) [12].

Compressed sensing (CS) in MRI demonstrates that it is possible to reconstruct MR images with diagnostic quality from a fewer measurements than that of the conventional approach which follows the Nyquist-Shannon sampling theorem [1, 6, 10, 18]. MR images possesses some favorable characteristics for signal processing such as they are compressible or s-sparse over a transform domain, like, wavelet transform. MRI signals naturally in the frequency domain or k-space which is to some extent incoherent with the wavelets.

Combination of CS with pMRI (CS-pMRI) is able to reduce MRI scan time significantly [23]. In CS-MRI traditional linear reconstruction is not possible. Since acquired data are highly undersampled, nonlinear reconstruction techniques need to be used for reconstruction. Computational time and quality of reconstruction are two major research issues in CS-MRI.

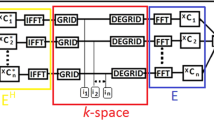
In 3D MRI, multiple 2D thin slices are acquired with a fixed and negligible inter-slice gaps followed by some post-processing techniques to generate a 3D volume for clinical studies. Since slices are thin (2–3 mm) and inter-slice gaps are very less, adjacent slices are highly correlated [7, 9]. In pMRI multiple receiver coils work in parallel. Data acquired by different coils are weighted differently due to the distinct spatial sensitivity profile of respective coils. Since target FoV is same for all receiver coils, structures and edges appear at same positions with different intensity values. To exploit data correlations that exist in multi-slice multi-channel MRI, we have used group-sparsity in both wavelet as well as spatial domains [8]. In this paper, we have proposed a fast calibrationless CS-pMRI reconstruction model using group-sparsity as regularization constraint. Since computational time is a major factor for the practical implementation of CS-pMRI reconstruction, we use a hybrid CPU-GPU platform for acceleration in CS reconstruction.

The rest of the paper is organized as follows: Sect. 2 briefly presents the background. Section 3 details the proposed group-sparsity based CS pMRI reconstruction technique. Next, experimental results and performance evaluations are done in Sect. 4, followed by conclusions in Sect. 5.

2 Background

Commonly, CS based MRI reconstruction model involves wavelet domain sparsity and spatial domain gradient sparsity as regularization constraints [18]. A standard CS pMRI reconstruction problem may be described as follows- suppose \(\mathbf {y}_q\in \mathcal {C}^m \) is measured k-space data corresponding to \(c^{\text {th}}\) coil image, \(\mathbf {x}_q \in \mathcal {C}^n\) i.e. \(\mathbf {y}_q=\mathbf {F}_u \mathbf {x}_q\), where \(m\ll n\), \(q=1,2,...,Q\); Q is number of coils, and \(\mathbf {F}_u \in \mathcal {C}^{m \times n}\) represent a partial Fourier operator [16]. To reconstruct image corresponding to \(q^{\text {th}}\) receiver coil, \(\mathbf {x}_q\) from \(\mathbf {y}_c\), need to solve following optimization problem:

$$\begin{aligned} \mathrm{{ \mathbf {\hat{x}}_q = }}\mathop {\mathrm{{argmin}}}\limits _{\mathbf {x}_q} \tfrac{1}{2}\mathrm{{ ||}}\mathbf {F}_u \mathbf {x}_q - \mathbf {y}_q\mathrm{{||}}_2^2 + \lambda _1 ||\,{{\varPsi }} \mathbf {x}_q||_1 \, + \lambda _2 \,||\mathbf {x}_q||_{\mathrm {TV}}, \end{aligned}$$
(1)

where \(\lambda _1\) and \(\lambda _2\) are regularization parameters to balance between data fidelity and regularization terms, \({\varPsi }\) wavelet transform operator, and \(||\mathbf {x}_q||_{\mathrm {TV}}\) is the TV norm of \(\mathbf {x}_q\) i.e. \(||\mathbf {x}_q||_{\mathrm {TV}} = \sum \limits _{i,j} {\sqrt{\left\{ (\nabla _h \mathbf {x}_q)_{i,j}\right\} ^2 + \left\{ (\nabla _v \mathbf {x}_q)_{i,j} \right\} ^2 }}\) where \(\nabla _h\) and \(\nabla _v\) are the first-order gradients in horizontal and vertical directions, respectively [11].

Reconstruction approaches may be classified into two categories depending on how coil sensitivity profiles of different receiver coils are used for reconstruction. First category explicitly require coil sensitivity profile information for reconstruction, like, in the sensitivity encoding (SENSE) [20] and the simultaneous acquisition of spatial harmonics (SMASH) [21]. SENSE gives optimal reconstruction performance if the coil information is accurate. In the second category, the coil sensitivity profile information is used implicitly during reconstruction, like, in the GRAPPA [13] and the AUTO-SMASH [15]. These methods estimate the coil sensitivity profile from the acquired raw data and known as auto-calibrating methods. Some of the well known auto-calibrating methods are- the SPIRiT [17], the CS-SENSE [16], and the ESPIRiT [22]. The main disadvantage associated with these methods is that in practice, it is very difficult to accurately estimate coil sensitivity profiles. A small error in estimation may lead to non-removable artifacts during reconstruction. Besides the above, there is another kind of CS based pMRI reconstruction approach which is relatively new, do not use coil sensitivity information explicitly or implicitly, known as the calibrationless methods, like, the CalM MRI [19].

According to Chen and Huang [2], wavelet coefficients of MR images are not only compressible but also have quadtree structure. The children coefficients in the finer scale are highly correlated with the parent coefficient in the adjacent coarser scale and may be modeled to follow the tree sparsity. In pMRI, images corresponding to different receiver coils of a particular FoV are similar. So, wavelet coefficients of different coil images of similar positions are expected to be similar. Chen et al. [3] exploit inter-channel similarity in wavelet domain during pMR image reconstruction. The concept of tree sparsity in a single image is extended to pMRI, where multiple wavelet trees of identical positions corresponding to different receiver coils are considered. They named it as the forest sparsity and corresponding reconstruction as FCSA Forest.

3 Proposed Method

In this paper, we have proposed a calibrationless pMRI reconstruction technique using group-sparsity in both wavelet as well as spatial domains. To exploit intra-channel, inter-channel/slice similarity in wavelet domain we have used forest sparsity i.e. wavelet tree groups of identical locations from multiple channels and slices. This particular grouping arrangement enforces similarity among the group members of the respective forest group. Similarly, we have used joint total variation (JTV)-norm to exploit data redundancy in spatial domain gradients as reported in JTV MRI [4].

Proposed multi-slice pMRI problem is as follows: suppose the measured undersampled k-space data \({{\mathbf {Y}} = \big \{ \big ({{\mathbf {y}}_{1,1},\,{\mathbf {y}}_{1,2} , \cdots ,\,{\mathbf {y}}_{1,Q} } \big );\big ( {{\mathbf {y}}_{2,1},\,{\mathbf {y}}_{2,2} , \cdots ,\,{\mathbf {y}}_{2,Q} } \big ); \,}\) \({ \cdots \,;\big ( {{\mathbf {y}}_{P,1} ,\,{\mathbf {y}}_{P,2} , \cdots ,\,\,{\mathbf {y}}_{P,Q} } \big )} \big \}\), corresponding to the underlying spatial domain multi-slice multi-channel data

\({\mathbf {X}} = \big \{ \big ( {\mathbf {x}}_{1,1} ,\,{\mathbf {x}}_{1,2} , \cdots ,\,{\mathbf {x}}_{1,Q} \big );\) \(\big ({\mathbf {x}}_{2,1}^{} ,\,{\mathbf {x}}_{2,2}^{} ,\cdots ,\) \(\,{\mathbf {x}}_{2,Q}^{} \big );\,\cdots \,;\, \big ({\mathbf {x}}_{P,1}^{} ,\,{\mathbf {x}}_{P,2}^{} , \cdots ,\) \(\,{\mathbf {x}}_{P,Q}^{} \big )\big \}\) such that \({\mathbf {Y}} = {\mathbf {F}}_u {\mathbf {X}}\) where P and Q is the number of slices and channels, respectively. We extended the model in Eq. 1 for joint reconstruction of multi-slice multi-channel data \({\mathbf {X}}\) from \({\mathbf {Y}}\) as follows:

$$\begin{aligned} \widehat{\mathbf {X}} = \mathop {\arg \min }\limits _{\mathbf {X}} \tfrac{1}{2}\sum \limits _{p = 1}^P {\sum \limits _{q = 1}^Q {||{\mathbf {F}}_u {\mathbf {x}}_{p,q} - {\mathbf {y}}_{p,q} ||_2^2 } } + \lambda _1 \sum \limits _{g_i \in {\text {G}}} {||\left( {\varPsi {\mathbf {X}}} \right) _{g_i } ||_2 }+ \lambda _2 \,||{\mathbf {X}}||_{{\text {JTV}}} , \end{aligned}$$
(2)

First regularization term is the wavelet forest sparsity which is mathematically denoted by \(\ell _{1,2}\)-norm, where \({g_i }\) contains the indices of wavelet coefficient of \(i^{\text {th}}\) group and G contains indices of all such groups, i.e. \(\mathrm {G}=\left[ g_1,\,\ldots ,\,g_i,\,\ldots , g_p\right] \). Next JTV-norm is given by- \(||{\mathbf {X}}||_{{\text {JTV}}} = \sum \limits _{i = 1,j = 1}^{\sqrt{n} ,\sqrt{n} } {\sqrt{\sum \limits _{p = 1,\,q = 1}^{P,\,Q} {\left\{ {\left( {\nabla _h \,{\mathbf {x}}_{p,q} } \right) _{i,j}^2 + \left( {\nabla _v \,{\mathbf {x}}_{p,q} } \right) _{i,j}^2 } \right\} } } }\). We decompose this problem into two smaller subproblems using the concept of variable splitting, first subproblem is based on wavelet forest sparsity and second subproblems is JTV based, as follows:

$$\begin{aligned} {\mathbf {Z}}= & {} \mathop {\arg \min }\limits _{\mathbf {Z}} \lambda _1 \sum \limits _{g_i \in {\text {G}}} {||{\mathbf {Z}}_{g_i } ||_2 } + \tfrac{\beta }{2}||{\mathbf {Z}} - G\varPsi {\mathbf {X}}||_2^2 \end{aligned}$$
(3)
$$\begin{aligned} \widehat{\mathbf {X}}= & {} \mathop {\arg \min }\limits _{\mathbf {X}} \tfrac{1}{2}\sum \limits _{p = 1}^P {\sum \limits _{q = 1}^Q {||{\mathbf {F}}_u {\mathbf {x}}_{p,q} - {\mathbf {y}}_{p,q} ||_2^2 } } + \tfrac{\beta }{2}||{\mathbf {Z}} - G\varPsi {\mathbf {X}}||_2^2 + \lambda _2 \,||{\mathbf {X}}||_{{\text {JTV}}} \end{aligned}$$
(4)

Above problems can be solved by the FCSA [14], the WaTMRI [2] and the FCSA Forest [3] algorithms as detailed in Algorithm 1.

figure a

4 Experimental Results and Simulations

Simulation works are carried out in the MATLAB running in a workstation having Intel Xeon processor E5-2650, 128 GB of memory, and NVIDIA Quadro P5000 GPU. We have collected several magnitude and raw complex MRI datasets from different sources. Since raw complex datasets are realistic for clinical CS-MRI implementations, we have considered two raw complex datasets for simulations of the proposed work. Dataset I: NYU machine learning dataFootnote 1 \((768 \times 770 \times 15 \times 31)\) and Dataset II: Stanford Fully sampled 3D FSE KneesFootnote 2 \((320 \times 320 \times 8 \times 172)\). Results are compared with other techniques, we have considered three well known auto-calibrating techniques, namely, the CS-SENSE [16], the SPIRiT [17], and the ESPIRiT [22]; and four calibrationless techniques, namely, the CaLM MRI [19], the JTV MRI [4], the FCSA-Forest [3], and the CaL JS CS SENSE [5]. We have considered two well-known image quality assessment (IQA) metrics, namely, the signal to noise ratio (SNR) and the mean structural similarity index (MSSIM) besides visual results and computational time. In the simulation, we have used 25% undersampling ratio for both datasets. We use “db2” wavelet and 4 decomposition levels for sparse representation.

Fig. 1.
figure 1

Comparison of reconstruction performances in terms of SNR and MSSIM for different datasets

Full size image
Fig. 2.
figure 2

Comparison of a reconstructed image (slice #10) from dataset I and corresponding error images using different techniques at 25% undersampling ratio. (a)–(j) output and error images using the CS SENSE, the SPIRiT, the CaLM MRI, the JTV-MRI, the FCSA Forest, the ESPIRiT, the CaL JS CS SENSE, and the proposed technique, respectively.

Full size image

To check the feasibility of practical implementations, we have done parallel implementation in a hybrid CPU-GPU simulation environment. 4D problems for each dataset is split into multiple smaller 4D subproblems. Each such subproblem contains three adjacent slices corresponding to 8 or 15 channels. Reconstruction performances in terms of SNR and MSSIM are shown in Fig. 1. Proposed technique outperforms all other methods for both datasets. Reconstructed images using different techniques corresponding to slice \(\# 10\) of Dataset I are shown in Fig. 2.

Table 1. Reconstruction time in terms of CPU Time (min.)
Full size table

It is clearly visible that the reconstructed image using the proposed method gives the least visible artifacts. Reconstruction time using different methods are shown in Table 1. In case of sequential implementation the proposed method takes the least computational time except for JTV MRI because the latter does not use the forest sparsity in the wavelet domain. The proposed parallel implementation method takes only 2 to 3 min for reconstruction of clinical datasets.

5 Conclusions

We have proposed a joint reconstruction technique for 4D CS MRI reconstruction. Performance of the proposed reconstruction technique is evaluated with two raw complex MRI datasets. Simulation results show that proposed technique outperforms the state-of-the-art. We have also implemented proposed technique in a hybrid CPU-GPU platform and observe that proposed method can able to produce reconstructed multi-dimensional MRI data within few minutes.