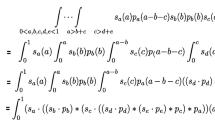Abstract
Metastasis is the mechanism by which cancer results in mortality and there are currently no reliable treatment options once it occurs, making the metastatic process a critical target for new diagnostics and therapeutics. Treating metastasis before it appears is challenging, however, in part because metastases may be quite distinct genomically from the primary tumors from which they presumably emerged. Phylogenetic studies of cancer development have suggested that changes in tumor genomics over stages of progression often results from shifts in the abundance of clonal cellular populations, as late stages of progression may derive from or select for clonal populations rare in the primary tumor. The present study develops computational methods to infer clonal heterogeneity and temporal dynamics across progression stages via deconvolution and clonal phylogeny reconstruction of pathway-level expression signatures in order to reconstruct how these processes might influence average changes in genomic signatures over progression. We show, via application to a study of gene expression in a collection of matched breast primary tumor and metastatic samples, that the method can infer coarse-grained substructure and stromal infiltration across the metastatic transition. The results suggest that genomic changes observed in metastasis, such as gain of the ErbB signaling pathway, are likely caused by early events in clonal evolution followed by expansion of minor clonal populations in metastasis (Algorithmic details, parameter settings, and proofs are provided in an Appendix with source code available at https://github.com/CMUSchwartzLab/BrM-Phylo).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Amaratunga, D., et al.: Analysis of data from viral DNA microchips. J. Am. Stat. Assoc. 96(456), 1161–1170 (2001)
Aster, J.C., et al.: The varied roles of Notch in cancer. Ann. Rev. Pathol. 12, 245–275 (2017)
Bell, R.M., et al.: Scalable collaborative filtering with jointly derived neighborhood interpolation weights. In: Seventh IEEE International Conference on Data Mining (ICDM 2007), pp. 43–52 (2007)
Brastianos, P.K., et al.: Genomic characterization of brain metastases reveals branched evolution and potential therapeutic targets. Cancer Discov. 5(11), 1164–1177 (2015)
de Bruin, E.C., et al.: Spatial and temporal diversity in genomic instability processes defines lung cancer evolution. Science (New York N.Y.) 346(6206), 251–256 (2014)
Chaffer, C.L., et al.: A perspective on cancer cell metastasis. Science 331(6024), 1559–1564 (2011)
Chambers, A.F., et al.: Dissemination and growth of cancer cells in metastatic sites. Nat. Rev. Cancer 2(8), 563–572 (2002)
Desmedt, C., et al.: Biological processes associated with breast cancer clinical outcome depend on the molecular subtypes. Clin. Cancer Res. 14(16), 5158–5165 (2008)
Desper, R., et al.: Tumor classification using phylogenetic methods on expression data. J. Theor. Biol. 228(4), 477–496 (2004)
Ding, L., et al.: Advances for studying clonal evolution in cancer. Cancer Lett. 340(2), 212–219 (2013)
Floyd, R.W.: Algorithm 97: shortest path. Commun. ACM 5(6), 344–348 (1962)
Funk, S.: Netflix update: try this at home (2006)
Greaves, M., et al.: Clonal evolution in cancer. Nature 481(7381), 306–313 (2012)
Guan, X.: Cancer metastases: challenges and opportunities. Acta Pharm. Sinica B 5(5), 402–418 (2015)
Gupta, S., et al.: Targeting the Hedgehog pathway in cancer. Ther. Adv. Med. Oncol. 2(4), 237–250 (2010)
Hofer, A.M., et al.: Extracellular calcium and cAMP: second messengers as “third messengers”? Physiology 22(5), 320–327 (2007)
Hosack, D.A., et al.: Identifying biological themes within lists of genes with EASE. Genome Biol. 4(10), R70–R70 (2003)
Huang, D.W., et al.: Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources. Nat. Protoc. 4(1), 44–57 (2009)
Kanehisa, M., et al.: KEGG: kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 28(1), 27–30 (2000)
Kingma, D., et al.: Adam: a method for stochastic optimization. In: International Conference on Learning Representations, December 2014
Körber, V., et al.: Evolutionary trajectories of IDHWT glioblastomas reveal a common path of early tumorigenesis instigated years ahead of initial diagnosis. Cancer Cell 35(4), 692–704 (2019)
Koren, Y., et al.: Matrix factorization techniques for recommender systems. Computer 42(8), 30–37 (2009)
Lee, D.D., et al.: Algorithms for non-negative matrix factorization. In: Proceedings of the 13th International Conference on Neural Information Processing Systems, NIPS 2000, pp. 535–541. MIT Press, Cambridge (2000)
Lee, S., et al.: Cytokines in cancer immunotherapy. Cancers 3(4), 3856–3893 (2011)
Lei, H., et al.: Tumor copy number deconvolution integrating bulk and single-cell sequencing data. In: Cowen, L.J. (ed.) RECOMB 2019. LNCS, vol. 11467, pp. 174–189. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17083-7_11
Lin, N.U., et al.: CNS metastases in breast cancer. J. Clin. Oncol. 22(17), 3608–3617 (2004)
Lu, C.L., et al.: The full Steiner tree problem. Theor. Comput. Sci. 306(1), 55–67 (2003)
Massagué, J.: TGF\(\beta \) in cancer. Cell 134(2), 215–230 (2008)
Nei, M., et al.: The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol. Biol. Evol. 4(4), 406–425 (1987)
Park, Y., et al.: Network-based inference of cancer progression from microarray data. IEEE/ACM Trans. Comput. Biol. Bioinf. 6(2), 200–212 (2009)
Priedigkeit, N., et al.: Intrinsic subtype switching and acquired ERBB2/HER2 amplifications and mutations in breast cancer brain metastases. JAMA Oncol. 3(5), 666–671 (2017)
Qiu, P., et al.: Extracting a cellular hierarchy from high-dimensional cytometry data with SPADE. Nat. Biotechnol. 29(10), 886–891 (2011)
Riester, M., et al.: A differentiation-based phylogeny of cancer subtypes. PLoS Comput. Biol. 6(5), e1000777 (2010)
Rumelhart, D.E., et al.: Learning representations by back-propagating errors. Nature 323, 533 (1986)
Schwartz, R., et al.: The evolution of tumour phylogenetics: principles and practice. Nat. Rev. Genet. 18, 213 (2017)
Schwartz, R., et al.: Applying unmixing to gene expression data for tumor phylogeny inference. BMC Bioinform. 11(1), 42 (2010)
Tao, Y., et al.: From genome to phenome: Predicting multiple cancer phenotypes based on somatic genomic alterations via the genomic impact transformer. In: Pacific Symposium on Biocomputing (2020)
Vareslija, D., et al.: Transcriptome characterization of matched primary breast and brain metastatic tumors to detect novel actionable targets. J. Natl Cancer Inst. 111(4), 388–398 (2018)
Ward, J.H.: Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 58(301), 236–244 (1963)
Warshall, S.: A theorem on boolean matrices. J. ACM 9(1), 11–12 (1962)
Witzel, I., et al.: Breast cancer brain metastases: biology and new clinical perspectives. Breast Cancer Res. 18(1), 8 (2016)
Wong, R.S.Y.: Apoptosis in cancer: from pathogenesis to treatment. J. Exp. Clinical Cancer Res. 30(1), 87 (2011)
Zhan, T., et al.: Wnt signaling in cancer. Oncogene 36, 1461 (2016)
Zhu, L., et al.: Metastatic breast cancers have reduced immune cell recruitment but harbor increased macrophages relative to their matched primary tumors. bioRxiv: 525071 (2019)
Funding
This work was supported in part by a grant from the Mario Lemieux Foundation, U.S. N.I.H. award R21CA216452, Pennsylvania Department of Health award 4100070287, Breast Cancer Alliance, Susan G. Komen for the Cure, and by a fellowship to Y.T. from the Center for Machine Learning and Healthcare at Carnegie Mellon University. The Pennsylvania Department of Health specifically disclaims responsibility for any analyses, interpretations or conclusions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix
A1 Transcriptome Data Preprocessing
We applied our methods to raw bulk RNA-Sequencing data of 44 matched primary breast and metastatic brain tumors from 22 patients (each patient gives two samples) [31, 38], where six patients are from the Royal College of Surgeons (RCS) and sixteen patients from the University of Pittsburgh (Pitt). These data profiled the expression levels of approximately 60,000 transcripts. We removed the genes that are not expressed in any sample. We also considered only protein-coding genes in the present study. We conducted quantile normalization across samples using the geometric mean to remove possible artifacts from different experiment batches [1]. The top 2.5% and bottom 2.5% of expressions were clipped to further reduce noise. Finally, we transformed the resulting bulk gene expression values into the log space and mapped those for each gene to the interval [0, 1] by a linear transformation.
A2 Mapping to Gene Modules and Cancer Pathways
The protein-coding gene expressions were mapped into both perturbed gene modules and cancer pathways, using the DAVID tool and external knowledge bases [18], as well as the cancer pathways in KEGG database [19]. This step compresses the high dimensional data and provides markers of cancer-related biological processes (Fig. 1 Step 1).
Gene Modules. Functionally similar genes are usually affected by a common set of somatic alterations [30] and therefore are co-expressed in the cells. These genes are believed to belong to the same “gene modules” [8, 37]. Inspired by the idea of gene modules, we fed a subset of 3,000 most informative genes out of the approximately 20,000 genes that have the largest variances into the DAVID tool for functional annotation clustering using several databases [18]. DAVID maps each gene to one or more modules. We did not force the genes to be mapped into disjunct modules because a gene may be involved in several biological functions and therefore more than one gene module. We removed gene modules that were not enriched (fold enrichment < 1.0) and kept the remaining \(m_1=109\) modules (and the corresponding annotated functions), where fold enrichment is defined as the EASE score of the current module to the geometric mean of EASE scores in all modules [17]. The gene module values of all the \(n=44\) samples were represented as a gene module matrix \(\mathbf B _M \in \mathbb {R}^{m_1 \times n}\). The i-th gene module value in j-th sample, \(\mathbf B _{M_{i,j}}\), was calculated by taking the sum of expressions of all the genes in the i-th module. Then \(\mathbf B _M\) was rescaled row-wise by taking the z-scores across samples to compensate for the effect of variable module sizes.
Cancer Pathways. Although gene module representation is able to capture the variances across samples and reduce the redundancy of raw gene expressions, it has two disadvantages: First of all, lack of interpretability. Specifically, some annotations assigned by DAVID are not directly related to biological functions, and the annotations of different modules may substantially overlap. Secondly, the key perturbed cancer pathways or functions may not be always the ones that vary most across samples. For example, genes in cancer-related KEGG pathways (hsa05200) [19] are not especially enriched in the top 3,000 genes with the largest expression variances. To make better use of prior knowledge on cancer-relevant pathways, we supplemented the generic DAVID pathway sets with a KEGG “cancer pathway” representation of samples \(\mathbf B _P \in \mathbb {R}^{m_2 \times n}\), where the number of cancer pathways \(m_2 = 24\). The cancer-related pathways in the KEGG database are cleaner and easier to explain, more orthogonal to each other, and contain critical signaling pathways to cancer development. We extracted the 23 cancer-related pathways from the following 3 KEGG pathway sets: Pathways in cancer (hsa05200), Breast cancer (hsa05224), and Glioma (hsa05214). An additional cancer pathway RET pathway was added, since it was found to be recurrently gained in the prior research [38]. See y-axis of Fig. 3d for the complete list of 24 cancer pathways. We considered all the \(\sim \)20,000 protein-coding genes other than top 3,000 genes. The following mapping of cancer pathways and transformation to z-scores were similar to that we did to map the gene modules.
Until this step, the raw gene expressions of n samples were transformed into the compressed gene module/pathway representation of samples \(\mathbf B = \begin{bmatrix} \mathbf B _M^\intercal , \mathbf B _P^\intercal \end{bmatrix}^\intercal \in \mathbb {R}^{m \times n}\), where \(m = m_1 + m_2\). The gene module representation \(\mathbf B _M\) serves for accurately deconvolving and unmixing the cell communities, while the pathway representation \(\mathbf B _P\) serves as markers/probes and for interpretation purposes.
A3 Deconvolution of Bulk Data
1.1 A3.1 Non-convexity of Deconvolution Problem
Theorem 1
The deconvolution problem Eqs. (1–3) below is not convex:
Proof
If the problem is convex, we should have: \(\forall \lambda \in (0,1)\), and \(\forall \mathbf C _x, \mathbf C _y, \mathbf F _x, \mathbf F _y\) in the feasible domain, the following inequality always holds:
However, for the following setting:
and \(\lambda = 0.5\), we have
This is contradictory to Eq. (10). \(\square \)
1.2 A3.2 Architecture Specifications of NND
In the NND architecture, \(\left| \mathbf X \right| \) applies element-wise absolute value, \(\text {cwn}\left( \mathbf X \right) \) column-wisely normalizes \(\mathbf X \), so that each column of the output sums up to 1. The two operations of Eq. (5) naturally rephrase and remove the two constraints in Eqs. (2–3), and meanwhile fit the framework of neural networks. An alternative to the absolute value operation \(\left| \mathbf X \right| \) might be rectified linear unit \(\text {ReLU}(\mathbf X )=\max \left( \mathbf 0 , \mathbf X \right) \). However, this activation function is unstable and leads to inferior performance in our case, since \(\mathbf X _{lj}\) will be fixed to zero once it becomes negative and will lose the chance to get updated in the following iterations. One may also want to replace the column-wise normalization \(\text {cwn}\left( \mathbf X \right) \) with softmax operation \(\text {softmax}(\mathbf X )\). However, the nonlinearity introduced by softmax actually changes the original optimization problem Eqs. (1–3) and the fitted \(\mathbf F \) is therefore not sparse.
1.3 A3.3 Hyperparameters of NND
We used an Adam optimizer with default momentum parameters and learning rate of \(1\times 10^{-5}\) [20]. The mini-batch technique is not required since the data size in our application is small enough not to require it (\(\mathbf B \in \mathbb {R}^{m\times n}\), \(m=133\), \(n=44\)). The training was run until convergence, when the relative decrease of training loss is smaller than \(\epsilon =1 \times 10^{-10}\) every 20,000 iterations.
1.4 A3.4 Fitting Ability of NND
One might be suspicious whether the neural network fits precisely in practice, since it is based on a simple gradient descent optimization. To validate the fitting ability of NND, we plotted the PCA of original samples \(\mathbf B \) and the fitted samples \(\hat{\mathbf{B }} = \mathbf C {} \mathbf F \) (Fig. 4). One can easily see that NND provides good model fits to the data.
PCA of pathway representation \(\mathbf B \) and nnMF fitted \(\hat{\mathbf{B }}\). Each dot represents the pathway values of a sample \(\mathbf B _{\cdot j}\) or fitted \(\hat{\mathbf{B }}_{\cdot j}\). The first two PCA dimensions of original data and fitted data are almost in the same positions, which indicates that NND is able to fit precisely in our application. The number of components is set to be \(k=5\) here.
Distribution of elements in fraction matrix \(\mathbf F ^{\star }\). Since each column of \(\mathbf F \) is forced to sum up to be one, a Laplacian prior is applied to the elements of matrix \(\mathbf F \). This leads to the sparsity of \(\mathbf F ^{\star }\): 24 out of its 220 elements (\(k\times n = 5\times 44\)) are zeros (threshold set to \(2.5 \times 10^{-2}\)).
1.5 A3.5 Sparsity of NND Results
See Fig. 5 for distribution of fraction matrix in NND deconvolution results.
1.6 A3.6 Cross-Validation of NND
In each fold of the CV, we used \(\hat{\mathbf{B }}=\mathbf C {} \mathbf F \) to only fit some randomly selected elements of \(\mathbf B \), and then the test error was calculated using the other elements of \(\mathbf B \). This was implemented by introducing two additional mask matrices \(\mathbf M _{\text {train}}, \mathbf M _{\text {test}} \in \{0, 1\}^{m \times n}\), which are in the same shape of \(\mathbf B \), and \(\mathbf M _{\text {train}}+\mathbf M _{\text {test}}=1^{m \times n}\). During the training time, with the same constraints in Eq. (5), the optimization goal is:
where \(\mathbf X \odot \mathbf Y \) is the Hadamard (element-wise) product. At the time of evaluation, given optimized \(\mathbf C ^{\star }\), \(\mathbf F _{\text {par}}^{\star }\), and therefore optimized \(\mathbf F ^{\star }=\text {cwn}\left( \left| \mathbf F _{\text {par}}^{\star } \right| \right) \) for the optimization problem during training, the test error was calculated on the test set: \( \left\| \mathbf M _{\text {test}} \odot \left( \mathbf B - \mathbf C ^{\star } \mathbf F ^{\star } \right) \right\| _\mathrm{Fr}^2\). We used 20-fold cross-validation on the NND, so in each fold 95% positions of \(\mathbf M _{\text {train}}\) and 5% positions of \(\mathbf M _{\text {test}}\) were 1s.
A4 Derivation of Quadractic Programming, \(\mathbf P (\mathcal {W})\), and \(\mathbf q (\mathcal {W}, \mathbf c )\)
Recall Sect. 2.5, for the phylogeny \(\mathcal {G} = (\mathcal {V}, \mathcal {E})\), the Steiner nodes are indexed as \(\mathcal {V}_S = \{1,2,...,k-2\}\) (\(\left| \mathcal {V}_S \right| =k-2\)), the extant nodes are indexed as \(\mathcal {V}_C = \{k-1,k,...,2k-2\}\) (\(\left| \mathcal {V}_C \right| =k\)). The i-th pathway values of Steiner nodes are denoted as \(\mathbf x = \left[ x_1, x_2,...,x_{k-2} \right] ^\intercal \in \mathbb {R}^{k-2}\), and values of extant nodes as \(\mathbf y = \left[ y_{k-1}, y_{k}, ..., y_{2k-2} \right] ^\intercal \in \mathbb {R}^{k}\). Since we consider each pathway dimension separately here, the subscript i for \(\mathbf x \) and \(\mathbf y \) is omitted for brevity. The weight of edge \((u, v) \in \mathcal {E}\) connecting nodes u and v is \(w_{u v}\) (\(1 \le u < v \le 2k-2\)). Denote \(\mathcal {W} = \{ w_{u v} \ |\ (u,v) \in \mathcal {E} \}\). The inference of the i-th element in the pathway vector of the Steiner nodes can be formulated as minimizing the elastic potential energy \(U(\mathbf x , \mathbf y ; \mathcal {W})\) shown below:
Theorem 2
Equation (16) can be further rephrased as a quadratic programming problem:
where \(\mathbf P (\mathcal {W})\) is a function that takes as input edge weights \(\mathcal {W}\) and outputs a matrix \(\mathbf P \in \mathbb {R}^{(k-2) \times (k-2)}\), \(\mathbf q (\mathcal {W}, \mathbf y )\) is a function that takes as input edge weights \(\mathcal {W}\) and vector \(\mathbf y \) and outputs a vector \(\mathbf q \in \mathbb {R}^{k-2}\).
Proof
Based on Eq. (16), \(U(\mathbf x , \mathbf y ; \mathcal {W}) \ge 0\). Each term inside the first summation (\(v \le k-2\)) can be written as:
where

Each term (\(v \ge k-1\)) inside the second summation can be rephrased as:
where

and \( C(w_{uv},y_v) = \frac{1}{2}w_{uv}y_v^2 \) is independent of \(\mathbf x \). Therefore the optimization in Eq. (16) can be calculated and written as below:
\(\square \)
Remark 1
The optimal \(\mathbf x ^\star \) of the Eq. (16), or the solution to the quadratic programming problem Eq. (17) can be solved by setting the gradient to be \(\mathbf 0 \):
Therefore,
Remark 2
Based on the proof, we can derive how to calculate the matrix \(\mathbf P (\mathcal {W})\) and vector \(\mathbf q (\mathcal {W}, \mathbf y )\).
Initialize the matrix and vector with zeros:
For each edge \((u, v) \in \mathcal {E}\) with weight \(w_{u v}\), there are two possibilities of nodes u and v: First, if both of them are Steiner nodes (\(u \le k-2\), \(v \le k-2\)), we update \(\mathbf P \) and keep \(\mathbf q \) the same:
Second, if u is Steiner node and v is an extant node (\(u \le k-2\), \(v \ge k-1\)), we update both \(\mathbf P \) and \(\mathbf q \):
We apply the same procedure to all dimension of pathways \(i = 1, 2, ..., m\) to get the full pathway values for each Steiner node.
A5 Differentially Expressed Cancer Pathways
Table 2 provides a list of the identified differentially expressed cancer pathways.
A6 Portions of Cell Communities in BrM Patients
Figure 6 shows the inferred cell community portions across the BrM samples. The figure displays, for each patient, the proportion of each community in the primary and the metastatic sample.
A7 Perturbed Cancer Pathways Along Phylogenies
Tables 3, 4, 5 and 6 provide a full list of perturbed pathways across the phylogenies for Case 1, 2, 3, and 4 in Fig. 3e.
Classification of BrM patients based on the consisted cell subcommunities in matched samples. There are 12 subcases of the 4 cases mentioned in Sect. 3.2. Specifically, there are 9 specific cases (Case 1a-i) in Case 1. Most patients (7) have all the five cell communities in both primary and metastatic samples (Case 1i). A few patients (4) have all communities in metastasis samples and all clones but community C3|P in primary samples. The element \(\mathbf F _{lj}\) is taken as 0 when it is smaller than a threshold \(2.5 \times 10^{-2}\), and therefore the l-th community is missing in the j-th sample.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Tao, Y., Lei, H., Lee, A.V., Ma, J., Schwartz, R. (2019). Phylogenies Derived from Matched Transcriptome Reveal the Evolution of Cell Populations and Temporal Order of Perturbed Pathways in Breast Cancer Brain Metastases. In: Bebis, G., Benos, T., Chen, K., Jahn, K., Lima, E. (eds) Mathematical and Computational Oncology. ISMCO 2019. Lecture Notes in Computer Science(), vol 11826. Springer, Cham. https://doi.org/10.1007/978-3-030-35210-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-35210-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-35209-7
Online ISBN: 978-3-030-35210-3
eBook Packages: Computer ScienceComputer Science (R0)