Abstract
We study the problem of drawing a dynamic graph, where each vertex appears in the graph at a certain time and remains in the graph for a fixed amount of time, called the window size. This defines a graph story, i.e., a sequence of subgraphs, each induced by the vertices that are in the graph at the same time. The drawing of a graph story is a sequence of drawings of such subgraphs. To support readability, we require that each drawing is straight-line and planar and that each vertex maintains its placement in all the drawings. Ideally, the area of the drawing of each subgraph should be a function of the window size, rather than a function of the size of the entire graph, which could be too large. We show that the graph stories of paths and trees can be drawn on a \(2W \times 2W\) and on an \((8W+1) \times (8W+1)\) grid, respectively, where W is the window size. These results yield linear-time algorithms. Further, we show that there exist graph stories of planar graphs whose subgraphs cannot be drawn within an area that is only a function of W.
This research was supported by MIUR Proj. “MODE” n\(^\circ \) 20157EFM5C, by MIUR Proj. “AHeAD” n\(^\circ \) 20174LF3T8, by MIUR-DAAD JMP n\(^\circ \) 34120, by H2020-MSCA-RISE Proj. “CONNECT” n\(^\circ \) 734922, and by Roma Tre University Proj. “GeoView”.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
We consider a graph that changes over time. Its vertices enter the graph one after the other and persist in the graph for a fixed amount of time, called the
 . We call such a dynamic graph a
. We call such a dynamic graph a
 . More formally, let V be the set of vertices of a graph G. Each vertex \(v \in V\) is equipped with a label \(\tau (v)\), which specifies the time instant at which v appears in the graph. The labeling \(\tau : V \rightarrow \{1,2,\dots , |V|\}\) is a bijective function specifying a total ordering for V. At any time t, the graph \(G_t\) is the subgraph of G induced by the set of vertices \(\{v \in V: t-W < \tau (v)\le t\}\). We denote a graph story by \(\langle G, \tau , W \rangle \).
. More formally, let V be the set of vertices of a graph G. Each vertex \(v \in V\) is equipped with a label \(\tau (v)\), which specifies the time instant at which v appears in the graph. The labeling \(\tau : V \rightarrow \{1,2,\dots , |V|\}\) is a bijective function specifying a total ordering for V. At any time t, the graph \(G_t\) is the subgraph of G induced by the set of vertices \(\{v \in V: t-W < \tau (v)\le t\}\). We denote a graph story by \(\langle G, \tau , W \rangle \).
We are interested in devising an algorithm for visualizing graph stories. The input of the algorithm is an entire graph story and the output is what we call a drawing story. A
 is a sequence of drawings of the graphs \(G_t\). The typical graph drawing conventions can be applied to a drawing story. E.g., a drawing story is planar, straight-line, or on the grid if all its drawings are planar, straight-line, or on the grid, respectively.
is a sequence of drawings of the graphs \(G_t\). The typical graph drawing conventions can be applied to a drawing story. E.g., a drawing story is planar, straight-line, or on the grid if all its drawings are planar, straight-line, or on the grid, respectively.
A trivial way for constructing a drawing story would be to first produce a drawing of G and then to obtain a drawing of \(G_t\), for each time t, by filtering out vertices and edges that do not belong to \(G_t\). However, if the number of vertices of G is much larger than W, this strategy might produce unnecessarily large drawings. Ideally, the area of the drawing of each graph \(G_t\) should be a (polynomial) function of W, rather than a function of the size of the entire graph.
In this paper we show that the graph stories of paths and trees can be drawn on a \(2W \times 2W\) and on an \((8W+1) \times (8W+1)\) grid, respectively, so that all the drawings of the story are straight-line and planar, and so that vertices do not change their position during the drawing story. Further, we show that there exist graph stories of planar graphs that cannot be drawn within an area that is only a function of W, if planarity is required and vertices are not allowed to change their position during the drawing story.
The visualization of dynamic graphs is a classic research topic in graph drawing. In what follows we compare our model and results with the literature. We can broadly classify the different approaches in terms of the following features [2]. (i) The objects that appear and disappear over time can be vertices or edges. (ii) The lifetime of the objects may be fixed or variable. (iii) The story may be entirely known in advance (off-line model) or not (on-line model). In this paper, the considered objects are vertices, the lifetime is fixed and the model is off-line.
A considerable amount of the literature on the theoretical aspects of dynamic graphs focuses on trees. In [3], the objects are edges, the lifetime W is fixed, and the model is on-line; an algorithm is shown for drawing a tree in \(O(W^3)\) area, under the assumption that the edges arrive in the order of a Eulerian tour of the tree. In [10], the objects are vertices, the lifetime W is fixed, the model is off-line (namely, the sequence of vertices is known in advance, up to a certain threshold k), and the vertices can move. A bound in terms of W and k is given on the total amount of movement of the vertices. In [22], each subgraph of the story is given (each subgraph is a tree, whereas the entire graph may be arbitrary), each object can have an arbitrary lifetime, the model is off-line, and the vertices can move. Aesthetic criteria as in the classical Reingold-Tilford algorithm [19] are pursued.
Other contributions consider more general types of graphs. In [15], the objects are edges, which enter the drawing and never leave it, the model is on-line, the considered graphs are outerplanar, and the vertices are allowed to move by a polylogarithmic distance. In [8], the objects are edges, the lifetime is fixed, and the model is off-line; NP-completeness is shown for the problem of computing planar topological drawings of the graphs in the story; other results for the topological setting are presented in [1, 21]. Further related results appear in [7, 11, 12, 16, 18, 20]; in particular, geometric simultaneous embeddings [4, 6] are closely related to the setting we consider in this paper. Contributions focused on the information-visualization aspects of dynamic graphs are surveyed in [2]; further, a survey on temporal graph problems appears in [17].
Missing proofs can be found in the full version of the paper [5].
2 Preliminaries
In this section, we present definitions and preliminaries.
Graphs and Drawings. We denote the set of vertices and edges of a graph G by V(G) and E(G), respectively. A
 of G maps each vertex in V(G) to a distinct point in the plane and each edge in E to Jordan arc between its end-points. A drawing is
of G maps each vertex in V(G) to a distinct point in the plane and each edge in E to Jordan arc between its end-points. A drawing is
 if each arc is a straight-line segment, it is
if each arc is a straight-line segment, it is
 if no two arcs intersect, except at a common endpoint, and it is
if no two arcs intersect, except at a common endpoint, and it is
 (or, a
(or, a
 ) if each vertex is mapped to a point with integer coordinates.
) if each vertex is mapped to a point with integer coordinates.
Rooted Ordered Forests and Their Drawings. A
 T is a tree with one distinguished vertex, called
T is a tree with one distinguished vertex, called
 and denoted by r(T). We denote by T(u) the subtree of T rooted at a node u.
and denoted by r(T). We denote by T(u) the subtree of T rooted at a node u.
A
 T is a rooted tree such that, for each vertex \(v\in V(T)\), a
T is a rooted tree such that, for each vertex \(v\in V(T)\), a
 (linear) order \(u_1,\dots ,u_k\) of the children of v is specified. A sequence \(\mathcal F = T_1,T_2,\dots ,T_k\) of rooted ordered trees is a
(linear) order \(u_1,\dots ,u_k\) of the children of v is specified. A sequence \(\mathcal F = T_1,T_2,\dots ,T_k\) of rooted ordered trees is a
 .
.
A
 drawing of a rooted tree T is such that each edge is represented by a curve monotonically increasing in the y-direction from a vertex to its parent. A
drawing of a rooted tree T is such that each edge is represented by a curve monotonically increasing in the y-direction from a vertex to its parent. A
 drawing \(\varGamma \) of a rooted forest \(\mathcal F\) is such that the drawing of each tree \(T_i \in \mathcal F\) in \(\varGamma \) is strictly-upward. A strictly-upward drawing of an ordered tree T is
drawing \(\varGamma \) of a rooted forest \(\mathcal F\) is such that the drawing of each tree \(T_i \in \mathcal F\) in \(\varGamma \) is strictly-upward. A strictly-upward drawing of an ordered tree T is
 if, for each vertex \(v\in V(T)\), the left-to-right order of the edges from v to its children in the drawing is the same as the order associated with v in T. A strictly-upward drawing of a rooted ordered forest \(\mathcal F\) is
if, for each vertex \(v\in V(T)\), the left-to-right order of the edges from v to its children in the drawing is the same as the order associated with v in T. A strictly-upward drawing of a rooted ordered forest \(\mathcal F\) is
 if the drawing of each tree \(T_i \in \mathcal F\) is order-preserving. The definitions of (
if the drawing of each tree \(T_i \in \mathcal F\) is order-preserving. The definitions of (
 )
)
 ,
,
 , and
, and
 drawings of (ordered) rooted trees and forests are similar.
drawings of (ordered) rooted trees and forests are similar.
Geometry. Given two points \(p_1\) and \(p_2\) in \(\mathbb {R}^2\), we denote by \([p_1,p_2]\) the closed straight-line segment connecting \(p_1\) and \(p_2\). The
 and
and
 of a grid \([a,b] \times [c,d]\) are \(|[a,b] \cap \mathbb {Z}|=b-a+1\) and \(|[c,d] \cap \mathbb {Z}|=d-c+1\), respectively. A grid drawing \(\varGamma \) of a graph
of a grid \([a,b] \times [c,d]\) are \(|[a,b] \cap \mathbb {Z}|=b-a+1\) and \(|[c,d] \cap \mathbb {Z}|=d-c+1\), respectively. A grid drawing \(\varGamma \) of a graph
 \(W\times H\) grid if \(\varGamma \) is enclosed by the bounding box of some grid of width W and height H, and
\(W\times H\) grid if \(\varGamma \) is enclosed by the bounding box of some grid of width W and height H, and
 grid \([a,b] \times [c,d]\) if \(\varGamma \) is enclosed by the bounding box of the grid \([a,b] \times [c,d]\).
grid \([a,b] \times [c,d]\) if \(\varGamma \) is enclosed by the bounding box of the grid \([a,b] \times [c,d]\).
Graph Stories. A graph story \(\langle G, \tau , W \rangle \) is naturally
 a sequence \(\langle G_1, G_2, \dots , G_{n+W-1} \rangle \); for any \(t \in \{1,\dots ,n+W-1\}\), the graph \(G_t\) is the subgraph of G induced by the set of vertices \(\{v \in V: t-W < \tau (v)\le t\}\). Clearly, \(|V(G_t)| \le W\). Note that \(G_1,G_2,\dots ,G_{W-1}\) are subgraphs of \(G_W\) and \(G_{n+1},G_{n+2},\dots ,G_{n+W-1}\) are subgraphs of \(G_n\), while each of \(G_t\) and \(G_{t+1}\) has a vertex that the other graph does not have, for \(t=W,\dots ,n-1\). A graph story \(\langle G, \tau , W\rangle \) in which G is a planar graph, a path, or a tree is a
a sequence \(\langle G_1, G_2, \dots , G_{n+W-1} \rangle \); for any \(t \in \{1,\dots ,n+W-1\}\), the graph \(G_t\) is the subgraph of G induced by the set of vertices \(\{v \in V: t-W < \tau (v)\le t\}\). Clearly, \(|V(G_t)| \le W\). Note that \(G_1,G_2,\dots ,G_{W-1}\) are subgraphs of \(G_W\) and \(G_{n+1},G_{n+2},\dots ,G_{n+W-1}\) are subgraphs of \(G_n\), while each of \(G_t\) and \(G_{t+1}\) has a vertex that the other graph does not have, for \(t=W,\dots ,n-1\). A graph story \(\langle G, \tau , W\rangle \) in which G is a planar graph, a path, or a tree is a
 , a
, a
 , or a
, or a
 , respectively.
, respectively.
A
 for \(\langle G, \tau , W \rangle \) is a sequence \(\langle \varGamma _1, \varGamma _2, \dots , \varGamma _{n+W-1} \rangle \) of drawings such that, for every \(t=1, \dots , n+W-1\): (i) \(\varGamma _t\) is a drawing of \(G_t\), (ii) a vertex v is drawn at the same position in all the \(\varGamma _t\)’s such that \(v \in V(G_t)\), and (iii) an edge (u, v) is represented by the same curve in all the \(\varGamma _t\)’s such that \((u,v) \in E(G_t)\). The above definition implies that the drawings \(\varGamma _1,\varGamma _2,\dots ,\varGamma _{W-1}\) are the restrictions of \(\varGamma _W\) to the vertices and edges of \(G_1,G_2,\dots ,G_{W-1}\), respectively, and that the drawings \(\varGamma _{n+1},\varGamma _{n+2},\dots ,\varGamma _{n+W-1}\) are the restrictions of \(\varGamma _n\) to the vertices and edges of \(G_{n+1},G_{n+2},\dots ,G_{n+W-1}\), respectively. Hence, an algorithm that constructs a drawing story only has to specify the drawings \(\varGamma _{W},\varGamma _{W+1},\dots ,\varGamma _{n}\).
for \(\langle G, \tau , W \rangle \) is a sequence \(\langle \varGamma _1, \varGamma _2, \dots , \varGamma _{n+W-1} \rangle \) of drawings such that, for every \(t=1, \dots , n+W-1\): (i) \(\varGamma _t\) is a drawing of \(G_t\), (ii) a vertex v is drawn at the same position in all the \(\varGamma _t\)’s such that \(v \in V(G_t)\), and (iii) an edge (u, v) is represented by the same curve in all the \(\varGamma _t\)’s such that \((u,v) \in E(G_t)\). The above definition implies that the drawings \(\varGamma _1,\varGamma _2,\dots ,\varGamma _{W-1}\) are the restrictions of \(\varGamma _W\) to the vertices and edges of \(G_1,G_2,\dots ,G_{W-1}\), respectively, and that the drawings \(\varGamma _{n+1},\varGamma _{n+2},\dots ,\varGamma _{n+W-1}\) are the restrictions of \(\varGamma _n\) to the vertices and edges of \(G_{n+1},G_{n+2},\dots ,G_{n+W-1}\), respectively. Hence, an algorithm that constructs a drawing story only has to specify the drawings \(\varGamma _{W},\varGamma _{W+1},\dots ,\varGamma _{n}\).
We only consider drawing stories \(\varGamma \) that are planar, straight-line, and on the grid. Storing each drawing in \(\varGamma \) would require \(\varOmega (n \cdot W)\) space in total. However, since each vertex has the same position in all the drawings where it appears, since edges are straight-line segments, and since any two consecutive graphs in a graph story differ by O(1) vertices, we can encode \(\varGamma \) in total O(n) space.
Let \(\varGamma \) be a straight-line drawing story of a graph story \(\langle G, \tau , W \rangle \) and let \(G'\) be a subgraph of G (possibly \(G'=G\)). The
 \(\varGamma \) is the straight-line drawing of \(G'\) in which each vertex has the same position as in every drawing \(\varGamma _t\in \varGamma \) where it appears. Note that the drawing of \(G'\) induced by \(\varGamma \) might have crossings even if \(\varGamma \) is planar. For a subset \(B \subseteq V(G)\), let G[B] be the subgraph of G induced by the vertices in B and let \(\varGamma [B]\) be the straight-line drawing of G[B] induced by \(\varGamma \).
\(\varGamma \) is the straight-line drawing of \(G'\) in which each vertex has the same position as in every drawing \(\varGamma _t\in \varGamma \) where it appears. Note that the drawing of \(G'\) induced by \(\varGamma \) might have crossings even if \(\varGamma \) is planar. For a subset \(B \subseteq V(G)\), let G[B] be the subgraph of G induced by the vertices in B and let \(\varGamma [B]\) be the straight-line drawing of G[B] induced by \(\varGamma \).
Given a graph story \(\langle G, \tau , W \rangle \), we will often consider a partition of V into
 \(B_1, \dots , B_h\), where \(h=\lceil \frac{n}{W}\rceil \). For \(i=1,\dots ,h\), the bucket \(B_i\) is the set of vertices v such that \((i-1)W+1 \le \tau (v) \le \min \{i\cdot W,n\}\). Note that all buckets have W vertices, except, possibly, for \(B_h\). We have the following useful property.
\(B_1, \dots , B_h\), where \(h=\lceil \frac{n}{W}\rceil \). For \(i=1,\dots ,h\), the bucket \(B_i\) is the set of vertices v such that \((i-1)W+1 \le \tau (v) \le \min \{i\cdot W,n\}\). Note that all buckets have W vertices, except, possibly, for \(B_h\). We have the following useful property.
Property 1
For any t, let \(i=\lceil \frac{t}{W}\rceil \). Then \(G_t\) is a subgraph of \(G[B_{i-1} \cup B_{i}]\).
3 Planar Graph Stories
In this section we prove a lower bound on the size of any drawing story of a planar graph story. Let \(n\equiv 0 \mod 3\). An n-vertex
 G contains the vertices and the edges of the 3-cycle \(C_{i} = (v_{i-2},v_{i-1},v_i)\), for \(i=3,6,\dots ,n\), plus the edges \((v_i,v_{i+3})\), for \(i=1,2,\dots ,n-3\). The nested triangles graphs with \(n\ge 6\) vertices are 3-connected and thus they have a unique combinatorial embedding (up to a flip) [23]. We have the following.
G contains the vertices and the edges of the 3-cycle \(C_{i} = (v_{i-2},v_{i-1},v_i)\), for \(i=3,6,\dots ,n\), plus the edges \((v_i,v_{i+3})\), for \(i=1,2,\dots ,n-3\). The nested triangles graphs with \(n\ge 6\) vertices are 3-connected and thus they have a unique combinatorial embedding (up to a flip) [23]. We have the following.
Theorem 1
Let \(\langle G, \tau , 9\rangle \) be a planar graph story such that G is an n-vertex nested triangles graph and \(\tau (v_i)=i\). Then any drawing story of \(\langle G, \tau , 9\rangle \) lies on a \(\varOmega (n) \times \varOmega (n)\) grid.
Proof
In order to prove the statement we show that, for any drawing story \(\varGamma \) of \(\langle G, \tau , 9\rangle \), the straight-line drawing of G induced by \(\varGamma \) is planar. Then the statement follows from well-known lower bounds in the literature [9, 13, 14].
Let \(\varGamma = \varGamma _1,\varGamma _2,\dots ,\varGamma _{n+8}\). Note that, for any \(m=9,12,\dots ,n\), the graph \(G_m\) contains the cycles \(C_{m-6}=(v_{m-8},v_{m-7},v_{m-6})\), \(C_{m-3}=(v_{m-5},v_{m-4},v_{m-3})\), and \(C_{m}=(v_{m-2},v_{m-1},v_{m})\). For any \(m=9,12,\dots ,n\), let \(H_m\) and \(I_m\) be the subgraphs of G induced by \(v_1,v_2,\dots ,v_{m}\) and by \(v_{m-5},v_{m-4},\dots ,v_{m}\), respectively, and let \(\varGamma ^H_m\) and \(\varGamma ^I_m\) be the drawings of \(H_m\) and \(I_m\) induced by \(\varGamma \), respectively.
Since \(G=H_n\), in order to show that the drawing of G induced by \(\varGamma \) is planar, it suffices to show that \(\varGamma ^H_m\) is planar, for each \(m=9,12,\dots ,n\). We prove this statement by induction on m. The induction also proves that the cycle \(C_m\) bounds a face of \(\varGamma ^H_m\) and of \(\varGamma ^I_m\).
Suppose first that \(m=9\). Then \(H_9=G_9\) and the drawing \(\varGamma ^H_9=\varGamma _9\) of \(G_9\) is planar since \(\varGamma \) is a planar straight-line drawing of \(\langle G, \tau , 9\rangle \) and \(\varGamma _9 \in \varGamma \). The 3-connectivity of \(H_9\) and \(I_9\) implies that \(C_9\) bounds a face of \(\varGamma ^H_9\) and \(\varGamma ^I_9\).
Suppose now that \(m>9\). We show that \(\varGamma ^H_m\) is planar. By induction, \(\varGamma ^H_{m-3}\) is planar. Thus, we only need to prove that no crossing is introduced by placing the vertices \(v_{m-2}\), \(v_{m-1}\), and \(v_m\), which belong to \(H_m\) and not to \(H_{m-3}\), in \(\varGamma ^H_{m-3}\) as they are placed in \(\varGamma _m\) and by drawing their incident edges as straight-line segments. First, by induction, the cycle \(C_{m-3}=(v_{m-5},v_{m-4},v_{m-3})\) bounds a face of \(\varGamma ^H_{m-3}\) and of \(\varGamma ^I_{m-3}\). Second, the vertices \(v_{m-2}\), \(v_{m-1}\), and \(v_{m}\), as well as their incident edges, lie inside such a face in \(\varGamma _m\). Namely, \(v_{m-2}\), \(v_{m-1}\), and \(v_{m}\) lie inside the same face of \(\varGamma ^I_{m-3}\) in \(\varGamma _m\), as otherwise the cycle \(C_m\) would cross edges of \(I_{m-3}\) in \(\varGamma _m\); further, the face of \(\varGamma ^I_{m-3}\) in which \(v_{m-2}\), \(v_{m-1}\), and \(v_{m}\) lie in \(\varGamma _m\) is incident to all of \(v_{m-5}\), \(v_{m-4}\), and \(v_{m-3}\), as otherwise the edges \((v_{m-5},v_{m-2})\), \((v_{m-4},v_{m-1})\), and \((v_{m-3},v_{m})\) would cross edges of \(I_{m-3}\) in \(\varGamma _m\); however, no face of \(\varGamma ^I_{m-3}\) other than the one delimited by \(C_{m-3}\) is incident to all of \(v_{m-5}\), \(v_{m-4}\), and \(v_{m-3}\). This proves the planarity of \(\varGamma ^H_{m}\). The induction and the proof of the theorem are completed by observing that \(C_{m}\) bounds a face of \(\varGamma ^H_m\) and \(\varGamma ^I_m\). \(\square \)
4 Path Stories
Let \(\langle G, \tau , W\rangle \) be a path story, where \(G=(v_1, v_2, \dots , v_n)\). Note that the ordering of V(G) given by the path is, in general, different from the ordering given by \(\tau \).
The
 of G are the sets \(B^x_i\), with \(i = 1, \dots , \lceil \frac{h+1}{2}\rceil \), such that \(B^x_1=B_1\), and \(B^x_i = B_{2i-2} \cup B_{2i-1}\), for \(i = 2, \dots , \lceil \frac{h+1}{2}\rceil \). Note that each x-bucket has 2W vertices, except for \(B_1\) and, possibly, the last x-bucket; see Fig. 1. The
of G are the sets \(B^x_i\), with \(i = 1, \dots , \lceil \frac{h+1}{2}\rceil \), such that \(B^x_1=B_1\), and \(B^x_i = B_{2i-2} \cup B_{2i-1}\), for \(i = 2, \dots , \lceil \frac{h+1}{2}\rceil \). Note that each x-bucket has 2W vertices, except for \(B_1\) and, possibly, the last x-bucket; see Fig. 1. The
 of G are the sets \(B^y_j\), with \(j = 1, \dots , \lceil \frac{h}{2}\rceil \), such that \(B^y_j = B_{2j-1} \cup B_{2j}\). Note that each y-bucket has 2W vertices, except possibly for the last y-bucket; see Fig. 1. Also, each vertex belongs to exactly one x-bucket and to exactly one y-bucket.
of G are the sets \(B^y_j\), with \(j = 1, \dots , \lceil \frac{h}{2}\rceil \), such that \(B^y_j = B_{2j-1} \cup B_{2j}\). Note that each y-bucket has 2W vertices, except possibly for the last y-bucket; see Fig. 1. Also, each vertex belongs to exactly one x-bucket and to exactly one y-bucket.
We now present the following theorem; its proof is similar in spirit to the proof that any two paths admit a simultaneous geometric embedding [6].
Theorem 2
For any path story \(\langle G, \tau , W \rangle \), it is possible to compute in O(n) time a drawing story that is planar, straight-line, and lies on a \(2W \times 2W\) grid.
Proof
Let G be the path \((v_1, v_2, \dots , v_n)\) and let \(h=\lceil \frac{n}{W}\rceil \) be the number of buckets of V(G). We now order the vertices in each x-bucket and in each y-bucket; this is done according to the ordering in which the vertices appear in the path G. Formally, for \(i=1,2,\dots ,\lceil \frac{h+1}{2}\rceil \), let \(x_i: B^x_i \rightarrow \{1,\dots ,|B^x_i|\}\) be a bijective function such that, for any \(v_a,v_b \in B^x_i\), we have \(x_i(v_a)<x_i(v_b)\) if and only if \(a<b\). Similarly, for \(i=1,2,\dots ,\lceil \frac{h}{2}\rceil \), let \(y_i: B^y_i \rightarrow \{1,\dots ,|B^y_i|\}\) be a bijective function such that, for any \(v_a,v_b \in B^y_i\), we have \(y_i(v_a)<y_i(v_b)\) if and only if \(a<b\). We assign the coordinates to the vertices of G in \(\varGamma \) as follows. For any vertex v of G, let \(B^x_i\) and \(B^y_j\) be the x-bucket and the y-bucket containing v, respectively. We place v at the point \((x_i(v),y_j(v))\) in all the drawings \(\varGamma _t \in \varGamma \) such that v belongs to \(G_t\). Also, we draw each edge as a straight-line segment.
We now prove that the constructed drawing story \(\varGamma \) satisfies the properties in the statement. Since x-buckets and y-buckets have size at most 2W, we have that each drawing \(\varGamma _t \in \varGamma \) lies on the \([1,2W] \times [1,2W]\) grid. We have the following.
Property 2
For \(i=1,\dots , \lceil \frac{h+1}{2}\rceil \), the straight-line drawing \(\varGamma [B^x_i]\) of \(G[B^x_i]\) is planar. For \(j=1,\dots ,\lceil \frac{h}{2}\rceil \), the straight-line drawing \(\varGamma [B^y_j]\) of \(G[B^y_j]\) is planar.
Proof
By Property 1, there exists an x-bucket \(B^x_i\) or a y-bucket \(B^y_j\) that contains \(V(G_t)\). Then \(\varGamma _t\) coincides with \(\varGamma [B^x_i]\) or with \(\varGamma [B^y_j]\), respectively, restricted to the vertices in \(V(G_t)\). By Property 2, we have that \(\varGamma _t\) is planar.
Finally, the time needed to compute \(\varGamma \) coincides with the time needed to compute the functions \(x_i\) and \(y_j\), for each \(i \in \{1,2,\dots , \lceil \frac{h+1}{2}\rceil \}\) and \(j \in \{1,2,\dots , \lceil \frac{h}{2}\rceil \}\). This can be done in total O(n) time as follows. For \(i=1,\dots ,n\), traverse the path G from \(v_1\) to \(v_n\). When a vertex \(v_k\) is considered, the buckets \(B^x_i\) and \(B^y_j\) where \(v_k\) should be inserted are determined in O(1) time; then \(v_k\) is inserted in each of these buckets as the currently last vertex. This process provides each x-bucket \(B^x_i\) and each y-bucket \(B^y_j\) with the desired orderings \(x_i\) and \(y_j\), respectively. \(\square \)
5 Tree Stories
In this section we show how to draw a tree story \(\langle T, \tau , W \rangle \). Our algorithm partitions V(T) into buckets \(B_1,\dots ,B_h\) and then partitions the subtrees of T induced by each bucket \(B_i\) into two rooted ordered forests. For odd values of i, the forests corresponding to \(B_i\) are drawn “close” to the y-axis, while for even values of i, the forests corresponding to \(B_i\) are drawn “close” to the x-axis. The drawings of these forests need to satisfy strong visibility properties, as edges of T might connect vertices in a bucket \(B_i\) with the roots of the forests corresponding to the bucket \(B_{i+1}\), and vice versa. We now introduce a drawing standard for (static) rooted ordered forests that guarantees these visibility properties.
For a vertex v in a drawing \(\varGamma \), denote by
 the half-line originating at v with slope \(-2\). Also, consider a horizontal half-line originating at v and directed rightward; rotate such a line in clockwise direction around v until it overlaps with
the half-line originating at v with slope \(-2\). Also, consider a horizontal half-line originating at v and directed rightward; rotate such a line in clockwise direction around v until it overlaps with
 ; this rotation spans a closed wedge centered at v, which we call the
; this rotation spans a closed wedge centered at v, which we call the
 of v and denote by
of v and denote by
 . We have the following definition.
. We have the following definition.
Definition 1
Let \(\mathcal F =T_1,T_2,\dots ,T_k\) be a rooted ordered forest, with a total of \(m \le W\) vertices. A
 \(\varGamma \) of \(\mathcal F\) is a planar straight-line strictly-upward strictly-leftward order-preserving grid drawing of \(\mathcal F\) such that:
\(\varGamma \) of \(\mathcal F\) is a planar straight-line strictly-upward strictly-leftward order-preserving grid drawing of \(\mathcal F\) such that:
-
(i)
\(\varGamma \) lies on the \([0,m-1] \times [4W-2m+2,4W]\) grid;
-
(ii)
the roots \(r(T_1),r(T_2),\dots ,r(T_k)\) lie along the segment \(\big [(0,2W+2),(0,4W)\big ]\), in this order from bottom to top, and \(r(T_k)\) lies on (0, 4W);
-
(iii)
the vertices of \(T_i\) have y-coordinates strictly smaller than the vertices of \(T_{i+1}\), for \(i=1,\dots ,k-1\);
-
(iv)
for each tree \(T_i\) and for each vertex v of \(T_i\), let \(u_1,u_2,\dots ,u_{\ell }\) be the children of v in left-to-right order; then the vertices of \(T_i(u_j)\) have y-coordinates strictly smaller than the vertices of \(T_i(u_{j+1})\), for \(j=1,\dots ,\ell -1\); and
-
(v)
for each vertex v of \(\mathcal F\), the wedge
 does not intersect \(\varGamma \) other than along
does not intersect \(\varGamma \) other than along
 .
.
We are going to use the following property.
Property 3
For each vertex v in a
 -drawing \(\varGamma \) of \(\mathcal F\), the wedge
-drawing \(\varGamma \) of \(\mathcal F\), the wedge
 contains the segment \(\big [(2W+2,0),(4W,0)\big ]\) in its interior.
contains the segment \(\big [(2W+2,0),(4W,0)\big ]\) in its interior.
We can similarly define
 -,
-,
 -, and
-, and

 ; in particular, a drawing of \(\mathcal F\) is a
; in particular, a drawing of \(\mathcal F\) is a
 -,
-,
 -, or
-, or
 - drawing if and only if it can be obtained from a
- drawing if and only if it can be obtained from a
 -drawing by a clockwise rotation around the origin of the Cartesian axes by \(90^\circ \), \(180^\circ \), or \(270^\circ \), respectively. A property similar to Property 3 can be stated for such drawings.
-drawing by a clockwise rotation around the origin of the Cartesian axes by \(90^\circ \), \(180^\circ \), or \(270^\circ \), respectively. A property similar to Property 3 can be stated for such drawings.
We now present an algorithm, called
 -Drawer, that constructs a
-Drawer, that constructs a
 -drawing \(\varGamma \) of \(\mathcal F =T_1,\dots ,T_k\). The algorithm
-drawing \(\varGamma \) of \(\mathcal F =T_1,\dots ,T_k\). The algorithm
 -Drawer constructs \(\varGamma \) by induction, primarily, on k and, secondarily, on the number of vertices m of \(\mathcal F\).
-Drawer constructs \(\varGamma \) by induction, primarily, on k and, secondarily, on the number of vertices m of \(\mathcal F\).
The base case of the algorithm
 -Drawer happens when \(m=1\) (and thus \(k=1\)); then we obtain \(\varGamma \) by placing \(r(T_1)\) at (0, 4W). In the first inductive case, we have \(k=1\) and \(m>1\); see Fig. 2. Let \(\mathcal F_1\) be the rooted ordered forest \(T_1(u_1),T_1(u_2),\dots ,T_1(u_{\ell _1})\), where \(u_1,u_2,\dots ,u_{\ell _1}\) are the children of \(r(T_1)\) in left-to-right order. Inductively construct a
-Drawer happens when \(m=1\) (and thus \(k=1\)); then we obtain \(\varGamma \) by placing \(r(T_1)\) at (0, 4W). In the first inductive case, we have \(k=1\) and \(m>1\); see Fig. 2. Let \(\mathcal F_1\) be the rooted ordered forest \(T_1(u_1),T_1(u_2),\dots ,T_1(u_{\ell _1})\), where \(u_1,u_2,\dots ,u_{\ell _1}\) are the children of \(r(T_1)\) in left-to-right order. Inductively construct a
 -drawing \(\varGamma _1\) of \(\mathcal F_1\). We obtain \(\varGamma \) by placing \(r(T_1)\) at (0, 4W) and by translating \(\varGamma _1\) one unit to the right and two units down. In the second inductive case, we have \(k>1\); see Fig. 3. We inductively construct a
-drawing \(\varGamma _1\) of \(\mathcal F_1\). We obtain \(\varGamma \) by placing \(r(T_1)\) at (0, 4W) and by translating \(\varGamma _1\) one unit to the right and two units down. In the second inductive case, we have \(k>1\); see Fig. 3. We inductively construct a
 -drawing \(\varGamma _1\) of \(T_1\) and a
-drawing \(\varGamma _1\) of \(T_1\) and a
 -drawing \(\varGamma _2\) of the rooted ordered forest \(\mathcal F_2 = T_2,T_3,\dots ,T_{k}\). Then, we obtain \(\varGamma \) from \(\varGamma _1\) and \(\varGamma _2\) by translating \(\varGamma _1\) down so that \(r(T_1)\) lies two units below the lowest vertex in \(\varGamma _2\). We have the following.
-drawing \(\varGamma _2\) of the rooted ordered forest \(\mathcal F_2 = T_2,T_3,\dots ,T_{k}\). Then, we obtain \(\varGamma \) from \(\varGamma _1\) and \(\varGamma _2\) by translating \(\varGamma _1\) down so that \(r(T_1)\) lies two units below the lowest vertex in \(\varGamma _2\). We have the following.
Lemma 1
The algorithm
 -Drawer constructs a
-Drawer constructs a
 -drawing of \(\mathcal F\) in O(m) time.
-drawing of \(\mathcal F\) in O(m) time.
Algorithms
 -Drawer,
-Drawer,
 -Drawer, and
-Drawer, and
 -Drawer that construct a
-Drawer that construct a
 -drawing, a
-drawing, a
 -drawing, and a
-drawing, and a
 -drawing of \(\mathcal F\) can be defined analogously.
-drawing of \(\mathcal F\) can be defined analogously.
We now go back to the problem of drawing a tree story \(\langle T, \tau , W \rangle \). Let \(n=|V(T)|\). Recall that V(T) is partitioned into buckets \(B_1,\dots ,B_h\), where \(h=\lceil \frac{n}{W} \rceil \). We now show how to partition the subtrees of T induced by each bucket into up to two rooted ordered forests, so that the algorithms
 -,
-,
 -,
-,
 -, and
-, and
 -Drawer can be exploited in order to draw such forests, thus obtaining a drawing story of \(\langle T, \tau , W \rangle \). We proceed in several phases as follows.
-Drawer can be exploited in order to draw such forests, thus obtaining a drawing story of \(\langle T, \tau , W \rangle \). We proceed in several phases as follows.
 We label each vertex v of T belonging to a bucket \(B_i\) with the label \(b(v)=i\) and we remove from T all the edges (u, v) such that \(|b(u)-b(v)|>1\). Observe that such edges are not visualized in a drawing story of \(\langle T, \tau , W \rangle \).
We label each vertex v of T belonging to a bucket \(B_i\) with the label \(b(v)=i\) and we remove from T all the edges (u, v) such that \(|b(u)-b(v)|>1\). Observe that such edges are not visualized in a drawing story of \(\langle T, \tau , W \rangle \).
 As T might be a forest because of the previous edge removal, we add dummy edges to T to turn it back into a tree, while ensuring that \(|b(u)-b(v)|\le 1\) for every edge (u, v) of T. This is possible due to the following.
As T might be a forest because of the previous edge removal, we add dummy edges to T to turn it back into a tree, while ensuring that \(|b(u)-b(v)|\le 1\) for every edge (u, v) of T. This is possible due to the following.
Lemma 2
Dummy edges can be added to T in total O(n) time so that T becomes a tree and every edge (u, v) of T is such that \(|b(u)-b(v)|\le 1\).
 We now root T at an arbitrary vertex r(T) in \(B_1\). A
We now root T at an arbitrary vertex r(T) in \(B_1\). A
 of T is a maximal connected component of T composed of vertices in the same bucket. We assign a
of T is a maximal connected component of T composed of vertices in the same bucket. We assign a
 \(b(P)=i\) to a pertinent component P if every vertex of P belongs to \(B_i\). We now construct the following sets \(R_1,R_2,\dots ,R_k\) of pertinent components of T; see Fig. 4. The set \(R_1\) only contains the pertinent component of T the vertex r(T) belongs to. For \(j>1\), the set \(R_j\) contains every pertinent component P of T such that (i) P does not belong to \(\bigcup ^{j-1}_{i=1} R_i\) and (ii) P contains a vertex that is adjacent to a vertex belonging to a pertinent component in \(R_{j-1}\).
\(b(P)=i\) to a pertinent component P if every vertex of P belongs to \(B_i\). We now construct the following sets \(R_1,R_2,\dots ,R_k\) of pertinent components of T; see Fig. 4. The set \(R_1\) only contains the pertinent component of T the vertex r(T) belongs to. For \(j>1\), the set \(R_j\) contains every pertinent component P of T such that (i) P does not belong to \(\bigcup ^{j-1}_{i=1} R_i\) and (ii) P contains a vertex that is adjacent to a vertex belonging to a pertinent component in \(R_{j-1}\).
By the construction of the \(R_j\)’s, since \(|b(u)-b(v)|\le 1\) for every edge (u, v) of T, and by the rooting of T, we have the following simple property.
Property 4
For every vertex \(v \in R_j\), each child of v belongs to either \(R_j\) or \(R_{j+1}\).
 Next, we turn T into an ordered tree. Consider any vertex v and let \(R_j\) be the set v belongs to. Then, by Proposition 4, each child of v is either in \(R_j\) or in \(R_{j+1}\). We set the left-to-right order of the children of v so that all those in \(R_j\) come first, in any order, and all those in \(R_{j+1}\) come next, in any order.
Next, we turn T into an ordered tree. Consider any vertex v and let \(R_j\) be the set v belongs to. Then, by Proposition 4, each child of v is either in \(R_j\) or in \(R_{j+1}\). We set the left-to-right order of the children of v so that all those in \(R_j\) come first, in any order, and all those in \(R_{j+1}\) come next, in any order.
 We now define rooted ordered forests. For \(i=1,\dots ,h\) with i odd, let
We now define rooted ordered forests. For \(i=1,\dots ,h\) with i odd, let
 (resp.,
(resp.,
 ) be the forest containing all the pertinent components P such that \(b(P)=i\) and such that \(P\in R_j\) with \(j \equiv 1 \mod 4\) (resp., \(j \equiv 3 \mod 4\)). Also, for \(i=1,\dots ,h\) with i even, let
) be the forest containing all the pertinent components P such that \(b(P)=i\) and such that \(P\in R_j\) with \(j \equiv 1 \mod 4\) (resp., \(j \equiv 3 \mod 4\)). Also, for \(i=1,\dots ,h\) with i even, let
 (resp.,
(resp.,
 ) be the forest containing all the pertinent components P such that \(b(P)=i\) and such that \(P\in R_j\) with \(j \equiv 2 \mod 4\) (resp., \(j \equiv 0 \mod 4\)). We have the following.
) be the forest containing all the pertinent components P such that \(b(P)=i\) and such that \(P\in R_j\) with \(j \equiv 2 \mod 4\) (resp., \(j \equiv 0 \mod 4\)). We have the following.
Observation 1
Let v be a vertex of T and u be its parent. Let \(R_i\) and \(R_j\) be the sets containing the pertinent components u and v belong to, respectively, where \(j=i\) or \(j = i+1\), by Property 4. Then the following cases are possible.
-
1a
If \(j=i\), then u and v both belong to either
 ,
,
 ,
,
 , or
, or
 .
. -
1b
If \(j=i+1\), then v is the root of a pertinent component in \(R_j\). Also, either:
-
(i)
i is odd,
 , and
, and
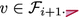 ;
; -
(ii)
i is even,
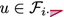 , and
, and
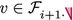 ;
; -
(iii)
i is odd,
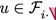 , and
, and
 ; or
; or -
(iv)
i is even,
 , and
, and
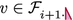 .
.
For each pertinent component P in any \(\mathcal F_{i \cdot X}\), with \(i\in \{1,\dots ,h\}\) and
 , let \(R_j\) be the set P belongs to. If \(j=1\), then the root of P is r(T), otherwise the root of P is the vertex of P that is adjacent to a vertex in \(R_{j-1}\). Further, the left-to-right order of the children of every vertex of P is the one inherited from T. Finally, the linear ordering of the pertinent components in \(\mathcal F_{i \cdot X}\) is defined as follows. Let \(P_1\) and \(P_2\) be any two pertinent components in \(\mathcal F_{i \cdot X}\) and let \(R_j\) and \(R_k\) be the sets containing \(P_1\) and \(P_2\), respectively. If \(j<k\), then \(P_1\) precedes \(P_2\) in \(\mathcal F_{i \cdot X}\). If \(j>k\), then \(P_1\) follows \(P_2\) in \(\mathcal F_{i \cdot X}\). Otherwise \(j=k\); let x be the lowest common ancestor of the roots of \(P_1\) and of \(P_2\) in T. Also, let \(p_1\) and \(p_2\) be the paths connecting the roots of \(P_1\) and of \(P_2\) with x, respectively. Further, let \(x_1\) and \(x_2\) be the children of x belonging to \(p_1\) and to \(p_2\), respectively. Then, \(P_1\) precedes \(P_2\) in \(\mathcal F_{i \cdot X}\) if and only if \(x_1\) precedes \(x_2\) in the left-to-right order of the children of x. We have the following.
, let \(R_j\) be the set P belongs to. If \(j=1\), then the root of P is r(T), otherwise the root of P is the vertex of P that is adjacent to a vertex in \(R_{j-1}\). Further, the left-to-right order of the children of every vertex of P is the one inherited from T. Finally, the linear ordering of the pertinent components in \(\mathcal F_{i \cdot X}\) is defined as follows. Let \(P_1\) and \(P_2\) be any two pertinent components in \(\mathcal F_{i \cdot X}\) and let \(R_j\) and \(R_k\) be the sets containing \(P_1\) and \(P_2\), respectively. If \(j<k\), then \(P_1\) precedes \(P_2\) in \(\mathcal F_{i \cdot X}\). If \(j>k\), then \(P_1\) follows \(P_2\) in \(\mathcal F_{i \cdot X}\). Otherwise \(j=k\); let x be the lowest common ancestor of the roots of \(P_1\) and of \(P_2\) in T. Also, let \(p_1\) and \(p_2\) be the paths connecting the roots of \(P_1\) and of \(P_2\) with x, respectively. Further, let \(x_1\) and \(x_2\) be the children of x belonging to \(p_1\) and to \(p_2\), respectively. Then, \(P_1\) precedes \(P_2\) in \(\mathcal F_{i \cdot X}\) if and only if \(x_1\) precedes \(x_2\) in the left-to-right order of the children of x. We have the following.
Lemma 3
Given the sets \(R_1,\dots ,R_k\), the rooted ordered forests \(\mathcal F_{i \cdot X}\), with \(i=1,\dots ,h\) and
 , can be computed in total O(n) time.
, can be computed in total O(n) time.
We are now ready to state the following main result.
Illustration for the proof of Theorem 3, with \(W=12\). The upper part of the figure shows the rooted ordered tree T; vertices and edges that are not in \(T[B_{1,2}]\) are gray. A pertinent component \(P^j_i\) of T belongs to the bucket \(B_i\); further, the index j represents the order of the components in the corresponding rooted forests. The lower part of the figure shows the drawing \(\varGamma [B_{1,2}]\) of \(T[B_{1,2}]\) constructed by the algorithm.
Theorem 3
For any tree story \(\langle T, \tau , W \rangle \) such that T has n vertices, it is possible to construct in O(n) time a drawing story that is planar, straight-line, and lies on an \((8W+1) \times (8W+1)\) grid.
Proof
We construct a planar straight-line drawing story \(\varGamma \) of \(\langle T, \tau , W \rangle \). We perform Phases 1–5 in order to construct the rooted ordered forests \(\mathcal F_{i\cdot X}\) with \(i\in \{1,\dots ,h\}\) and
 . Note that Phase 2 introduces in T some dummy edges, which are removed from the actual drawing story of \(\langle T, \tau , W \rangle \) after the construction of \(\varGamma \). Since \(\varGamma \) is a straight-line drawing, we only need to assign coordinates to the vertices of T; see Fig. 4. We apply the algorithm X-Drawer to construct an X-drawing \(\varGamma _{i\cdot X}\) of each rooted ordered forest \(\mathcal F_{i\cdot X}\). We let the coordinates of each vertex v of \(\mathcal F_{i\cdot X}\) in \(\varGamma \) coincide with its coordinates in \(\varGamma _{i\cdot X}\).
. Note that Phase 2 introduces in T some dummy edges, which are removed from the actual drawing story of \(\langle T, \tau , W \rangle \) after the construction of \(\varGamma \). Since \(\varGamma \) is a straight-line drawing, we only need to assign coordinates to the vertices of T; see Fig. 4. We apply the algorithm X-Drawer to construct an X-drawing \(\varGamma _{i\cdot X}\) of each rooted ordered forest \(\mathcal F_{i\cdot X}\). We let the coordinates of each vertex v of \(\mathcal F_{i\cdot X}\) in \(\varGamma \) coincide with its coordinates in \(\varGamma _{i\cdot X}\).
We now prove that \(\varGamma \) satisfies the properties in the statement of the theorem. By Condition i of Definition 1, a
 -drawing lies on the \([0,4W] \times [0,4W]\) grid. Similarly, a
-drawing lies on the \([0,4W] \times [0,4W]\) grid. Similarly, a
 -, a
-, a
 -, and a
-, and a
 -drawing lies on the \([0,4W] \times [-4W,0]\) grid, on the \([-4W,0] \times [-4W,0]\) grid, and on the \([-4W,0] \times [0,4W]\) grid, respectively. Thus, \(\varGamma \) lies on the \([-4W,4W] \times [-4W,4W]\) grid.
-drawing lies on the \([0,4W] \times [-4W,0]\) grid, on the \([-4W,0] \times [-4W,0]\) grid, and on the \([-4W,0] \times [0,4W]\) grid, respectively. Thus, \(\varGamma \) lies on the \([-4W,4W] \times [-4W,4W]\) grid.
Concerning the running time for the construction of \(\varGamma \), we have that the initial modification of T, which ensures that \(|b(u)-b(v)|\le 1\) for every edge (u, v) of T, can be done in O(n) time, by Lemma 2. The labeling b(u) of each vertex u of T is easily done in O(n) time. The construction of the sets \(R_1,\dots ,R_k\) can be accomplished by an O(n)-time traversal of T starting from r(T). The construction of the rooted ordered forests \(\mathcal F_{i\cdot X}\), with \(i=1,\dots ,h\) and with
 , can be performed in total O(n) time by Lemma 3. Finally, by Lemma 1, the algorithm X-Drawer runs in linear time in the size of its input \(\mathcal F_{i\cdot X}\).
, can be performed in total O(n) time by Lemma 3. Finally, by Lemma 1, the algorithm X-Drawer runs in linear time in the size of its input \(\mathcal F_{i\cdot X}\).
It remains to show that each drawing \(\varGamma _t \in \varGamma \) is planar. We exploit the following lemma. Let \(B_{i,i+1}=B_i \cup B_{i+1}\).
Lemma 4
For \(i=1,\dots ,h-1\), the drawing \(\varGamma [B_{i,i+1}]\) of \(T[B_{i,i+1}]\) is planar.
Proof
Suppose that i is odd; the case in which i is even can be treated analogously. Let (u, v) and (w, z) be any two edges of \(T[B_{i,i+1}]\). We prove that (u, v) and (w, z) do not cross in \(\varGamma [B_{i,i+1}]\). We only discuss the most interesting case, in which u and w both belong to
 and v and z both belong to
and v and z both belong to
 ; see the full version of the paper for a proof that covers the other cases.
; see the full version of the paper for a proof that covers the other cases.
By Observation 1
 , we have that v and z are the roots of two pertinent components \(P_v\) and \(P_z\) of
, we have that v and z are the roots of two pertinent components \(P_v\) and \(P_z\) of
 , respectively. By Condition ii of Definition 1, the vertices v and z lie on the segment \(\big [(2W+2,0),(4W,0)\big ]\). Assume w.l.o.g. that z lies to the right of v. We have the following.
, respectively. By Condition ii of Definition 1, the vertices v and z lie on the segment \(\big [(2W+2,0),(4W,0)\big ]\). Assume w.l.o.g. that z lies to the right of v. We have the following.
Claim 1
The vertex w lies above the vertex u in \(\varGamma [B_{i,i+1}]\).
Proof
Let \(R_j\) and \(R_k\) be the sets containing v and z, respectively. By the construction of
 and since z lies to the right of v, two cases are possible.
and since z lies to the right of v, two cases are possible.
In the first case \(j<k\). By Observation 1
 , we have that u and w belong to \(R_{j-1}\) and \(R_{k-1}\), respectively. Since \(j-1<k-1\), we have that u and w belong to distinct pertinent components \(P_u\) and \(P_w\) of T, respectively, where \(P_u\) precedes \(P_w\) in
, we have that u and w belong to \(R_{j-1}\) and \(R_{k-1}\), respectively. Since \(j-1<k-1\), we have that u and w belong to distinct pertinent components \(P_u\) and \(P_w\) of T, respectively, where \(P_u\) precedes \(P_w\) in
 . By Condition iii of Definition 1, we have that w lies above u in \(\varGamma [B_{i,i+1}]\).
. By Condition iii of Definition 1, we have that w lies above u in \(\varGamma [B_{i,i+1}]\).
In the second case \(j=k\). Let x be the lowest common ancestor of v and z in T. Also, let \(v'\) and \(z'\) be the children of x on the paths from x to v and z, respectively. Then \(v'\) precedes \(z'\) in the left-to-right order of the children of x. Note that \(j-1=k-1\) and that x is also the lowest common ancestor of u and w in T, where u lies on the path between v and x and w lies on the path between z and x.
If u and w belong to distinct pertinent components \(P_u\) and \(P_w\) of T then, as in the first case, \(P_u\) precedes \(P_w\) in
 . By Condition iii of Definition 1 we have that w lies above u in \(\varGamma [B_{i,i+1}]\).
. By Condition iii of Definition 1 we have that w lies above u in \(\varGamma [B_{i,i+1}]\).
If u and w belong to the same pertinent component of T and neither of them is x, then by Condition iv of Definition 1 we have that w lies above u in \(\varGamma [B_{i,i+1}]\).
If u and w belong to the same pertinent component of T and \(w=x\), then we have that w lies above u in \(\varGamma [B_{i,i+1}]\) since
 is strictly-upward.
is strictly-upward.
Finally, note that \(u\ne x\). Indeed, suppose, for a contradiction, that u is the lowest common ancestor of v and z. By the choice of the left-to-right ordering of the children of u (given in Phase 4), we have that \(z'\) precedes v in this ordering. Therefore, by the construction of the ordering of
 (given in Phase 5), we have that \(P_z\) precedes \(P_v\) in
(given in Phase 5), we have that \(P_z\) precedes \(P_v\) in
 ; by Condition ii of Definition 1, this contradicts the assumption that z lies to the right of v. \(\square \)
; by Condition ii of Definition 1, this contradicts the assumption that z lies to the right of v. \(\square \)
By Claim 1 and by Condition i of Definition 1, we have that w lies above u, which lies above v and z; recall that these last two vertices lie on the segment \(\big [(2W+2,0),(4W,0)\big ]\). Hence, the edge (u, v) crosses the edge (w, z) if and only if u lies to the right of the edge (w, z). By Property 3, the edge (w, z) lies in the wedge
 , except at w. However, if u lies to the right of the edge (w, z), then
, except at w. However, if u lies to the right of the edge (w, z), then
 contains u, which contradicts Condition v of Definition 1. \(\square \)
contains u, which contradicts Condition v of Definition 1. \(\square \)
By Property 1 and Lemma 4, we have that \(\varGamma \) is planar. \(\square \)
6 Conclusions and Open Problems
We have shown how to draw dynamic trees with straight-line edges, using an area that only depends on the number of vertices that are simultaneously present in the tree, while maintaining planarity. This result is obtained by partitioning the vertices of the tree into buckets and by establishing topological and geometric properties for the forests induced by pairs of consecutive buckets. Further, we proved that this result cannot be generalized to arbitrary planar graphs.
Several interesting problems arise. (OP1) Which families of planar graphs admit a planar straight-line drawing story on a grid whose size is polynomial in W? How about outerplanar graphs? (OP2) Which bounds can be shown for a dynamic graph that is not a tree, while each graph of the story is a forest?
References
Angelini, P., Bekos, M.A.: Hierarchical partial planarity. Algorithmica 81(6), 2196–2221 (2019). https://doi.org/10.1007/s00453-018-0530-6
Beck, F., Burch, M., Diehl, S., Weiskopf, D.: The state of the art in visualizing dynamic graphs. In: Borgo, R., Maciejewski, R., Viola, I. (eds.) Eurographics Conference on Visualization, EuroVis 2014 - State of the Art Reports, STARs, Swansea, UK, 9–13 June 2014. Eurographics Association (2014). https://doi.org/10.2312/eurovisstar.20141174
Binucci, C., Brandes, U., Di Battista, G., Didimo, W., Gaertler, M., Palladino, P., Patrignani, M., Symvonis, A., Zweig, K.A.: Drawing trees in a streaming model. Inf. Process. Lett. 112(11), 418–422 (2012). https://doi.org/10.1016/j.ipl.2012.02.011
Bläsius, T., Kobourov, S.G., Rutter, I.: Simultaneous embedding of planar graphs. In: Tamassia, R. (ed.) Handbook on Graph Drawing and Visualization, pp. 349–381. Chapman and Hall/CRC (2013)
Borrazzo, M., Da Lozzo, G., Frati, F., Patrignani, M.: Graph stories in small area. CoRR abs/1908.09318 (2019)
Braß, P., Cenek, E., Duncan, C.A., Efrat, A., Erten, C., Ismailescu, D., Kobourov, S.G., Lubiw, A., Mitchell, J.S.B.: On simultaneous planar graph embeddings. Comput. Geom. 36(2), 117–130 (2007). https://doi.org/10.1016/j.comgeo.2006.05.006
Cohen, R.F., Di Battista, G., Tamassia, R., Tollis, I.G.: Dynamic graph drawings: trees, series-parallel digraphs, and planar ST-digraphs. SIAM J. Comput. 24(5), 970–1001 (1995). https://doi.org/10.1137/S0097539792235724
Da Lozzo, G., Rutter, I.: Planarity of streamed graphs. In: Paschos, V.T., Widmayer, P. (eds.) CIAC 2015. LNCS, vol. 9079, pp. 153–166. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-18173-8_11
de Fraysseix, H., Pach, J., Pollack, R.: How to draw a planar graph on a grid. Combinatorica 10(1), 41–51 (1990)
Demetrescu, C., Di Battista, G., Finocchi, I., Liotta, G., Patrignani, M., Pizzonia, M.: Infinite trees and the future. In: Kratochvíyl, J. (ed.) GD 1999. LNCS, vol. 1731, pp. 379–391. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-46648-7_39
Di Battista, G., Tamassia, R.: On-line planarity testing. SIAM J. Comput. 25(5), 956–997 (1996). https://doi.org/10.1137/S0097539794280736
Di Battista, G., Tamassia, R., Vismara, L.: Incremental convex planarity testing. Inf. Comput. 169(1), 94–126 (2001). https://doi.org/10.1006/inco.2001.3031
Dolev, D., Leighton, F., Trickey, H.: Planar embedding of planar graphs. Adv. Comput. Res. 2, 147–161 (1984)
Frati, F., Patrignani, M.: A note on minimum-area straight-line drawings of planar graphs. In: Hong, S.-H., Nishizeki, T., Quan, W. (eds.) GD 2007. LNCS, vol. 4875, pp. 339–344. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-77537-9_33
Goodrich, M.T., Pszona, P.: Streamed graph drawing and the file maintenance problem. In: Wismath, S., Wolff, A. (eds.) GD 2013. LNCS, vol. 8242, pp. 256–267. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-03841-4_23
Italiano, G.F.: Fully dynamic planarity testing. In: Kao, M.Y. (ed.) Encyclopedia of Algorithms, pp. 806–808. Springer, New York (2016). https://doi.org/10.1007/978-1-4939-2864-4_157
Michail, O.: An introduction to temporal graphs: an algorithmic perspective. Internet Math. 12(4), 239–280 (2016)
Poutré, J.A.L.: Alpha-algorithms for incremental planarity testing (preliminary version). In: Leighton, F.T., Goodrich, M.T. (eds.) Proceedings of the Twenty-Sixth Annual ACM Symposium on Theory of Computing, Montréal, Québec, Canada, 23–25 May 1994, pp. 706–715. ACM (1994). https://doi.org/10.1145/195058.195439
Reingold, E.M., Tilford, J.S.: Tidier drawings of trees. IEEE Trans. Softw. Eng. 7(2), 223–228 (1981). https://doi.org/10.1109/TSE.1981.234519
Rextin, A., Healy, P.: A fully dynamic algorithm to test the upward planarity of single-source embedded digraphs. In: Tollis, I.G., Patrignani, M. (eds.) GD 2008. LNCS, vol. 5417, pp. 254–265. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00219-9_24
Schaefer, M.: Picking planar edges; or, drawing a graph with a planar subgraph. In: Duncan, C., Symvonis, A. (eds.) GD 2014. LNCS, vol. 8871, pp. 13–24. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45803-7_2
Skambath, M., Tantau, T.: Offline drawing of dynamic trees: algorithmics and document integration. In: Hu, Y., Nöllenburg, M. (eds.) GD 2016. LNCS, vol. 9801, pp. 572–586. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-50106-2_44
Whitney, H.: Congruent graphs and the connectivity of graphs. Am. J. Math. 54(1), 150–168 (1932). http://www.jstor.org/stable/2371086
Acknowledgments
We are indebted to Giuseppe Di Battista for interesting conversations and suggestions that helped us improve and direct our investigation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Borrazzo, M., Da Lozzo, G., Frati, F., Patrignani, M. (2019). Graph Stories in Small Area. In: Archambault, D., Tóth, C.D. (eds) Graph Drawing and Network Visualization. GD 2019. Lecture Notes in Computer Science(), vol 11904. Springer, Cham. https://doi.org/10.1007/978-3-030-35802-0_41
Download citation
DOI: https://doi.org/10.1007/978-3-030-35802-0_41
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-35801-3
Online ISBN: 978-3-030-35802-0
eBook Packages: Computer ScienceComputer Science (R0)





 does not intersect
does not intersect  .
.
 -drawing: the first inductive case, in which
-drawing: the first inductive case, in which 
 -drawing: the second inductive case, in which
-drawing: the second inductive case, in which  ,
,
 ,
,
 , or
, or
 .
. , and
, and
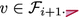 ;
;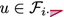 , and
, and
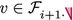 ;
;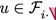 , and
, and
 ; or
; or , and
, and
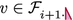 .
.