Abstract
We construct private-key and public-key functional encryption schemes in the bounded-key setting; that is, secure against adversaries that obtain an a-priori bounded number of functional keys (also known as the collusion bound).
An important metric considered in the literature on bounded-key functional encryption schemes is the dependence of the running time of the encryption algorithm on the collusion bound \(Q=Q(\lambda )\) (where \(\lambda \) is the security parameter). It is known that bounded-key functional encryption schemes with encryption complexity growing with \(Q^{1-\varepsilon }\), for any constant \(\varepsilon > 0\), implies indistinguishability obfuscation. On the other hand, in the public-key setting, it was previously unknown whether we could achieve encryption complexity growing linear with Q, also known as optimal bounded-key FE, based on well-studied assumptions.
In this work, we give the first construction of an optimal bounded-key public-key functional encryption scheme under the minimal assumption of the existence of any public-key encryption scheme. Moreover, our scheme supports the class of all polynomial-size circuits.
Our techniques also extend to the private-key setting. We achieve a construction of an optimal bounded-key functional encryption in the private-key setting based on the minimal assumption of one-way functions, instead of learning with errors as achieved in prior works.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Functional Encryption [SW05, BSW11] (FE) is a powerful type of encryption where the owner of a secret key \(\mathsf {sk}\) can generate special-purpose functional secret keys \(\mathsf {sk}_F\) which allow anyone to compute F(x) given an encryption of x. The standard and demanding security notion for functional encryption is collusion-resistance which, informally stated, requires that an adversary who holds functional secret keys for an arbitrary polynomial number of boolean functions \(F_1, F_2,\ldots , F_m\) of her choice should learn no more than \(F_1(x), F_2(x),\ldots , F_m(x)\) given an encryption of x. Collusion-resistant functional encryption schemes are extremely powerful: [AJ15, BV15, AJS15] show that such FE schemes can be used to construct indistinguishability obfuscators and therefore, can be used to instantiate a vast majority of cryptographic primitives (see [SW14] and a large number of followup works.) It is no surprise then that collusion-resistant FE schemes are very hard to construct and indeed, to this date, we do not know constructions from well-established cryptographic assumptions.
In many uses of functional encryption, however, the weaker notion of bounded-key setting might suffice. Bounded-key setting permits the secret-key owner to release an a priori bounded number \(Q=Q(\lambda )\) of functional keys. (Here and henceforth, \(\lambda \) denotes the security parameter.) Thus, bounded-key setting is appropriate in scenarios where functional keys are tied to users, and a large colluding set of users is hard to form. Historically, bounded-collusion resistance has been well-studied with the goals of improving efficiency, reducing computational assumptions, and supporting a larger class of functions; see [DKXY02, HK04, CHH+07, GLW12, SS10, GVW12a, ISV+17, AR17, Agr17] and the references therein.
Encryption Complexity. An important complexity measure considered in the FE literature is encryption complexity (defined to be the size of the encryption circuit). Of particular interest in the setting of bounded-collusion resistance (referred as bounded-key FE) is the growth of the encryption complexity with the collusion bound Q. The importance of this measure stems from the recent results [BV15, AJ15, AJS15, GS16, LM16, BNPW16, KNT18], which tell us that, for any constant \(\epsilon > 0\), bounded-key FE with encryption complexity \(Q^{1-\epsilon }\cdot \mathsf {poly}(\lambda ,s)\), where s is the maximum size of the functions queried, is as powerful as collusion-resistant FE. Thus, achieving encryption complexity \(Q^{1-\epsilon }\cdot \mathsf {poly}(\lambda ,s)\) in bounded-key FE schemes from well-studied assumptions would be a breakthrough in cryptography.
On the other hand, we could still hope to base bounded-key FE schemes, in the public-key setting, with encryption complexity \(Q \cdot \mathsf {poly}(\lambda ,s)\) (henceforth, referred to as optimal bounded-key FE) on well-studied assumptions. Unfortunately, this question has remained unanswered so far. The best known result, by Agrawal and Rosen [AR17], managed to reduce the encryption complexity to \(Q^2 + \mathsf {poly}(\lambda ,s)\).
We ask the following question:

1.1 Our Results
In this work, we answer the above question in the affirmative and in fact, our construction can be based on minimal assumptions alone, i.e., existence of any public-key encryption scheme.
Specifically, we prove the following theorem.
Theorem 1 (Informal)
Assuming the existence of public-key encryption, there exists a bounded-key public-key FE scheme for \(\mathsf {P}/\mathsf {Poly}\) with encryption complexity \(Q \cdot \mathsf {poly}(\lambda ,s)\), where Q is the collusion bound and s is the maximum size of the functions queried.
Additionally our scheme has many advantages. It satisfies simulation security and adaptive security, which is the best possible security notion that we can achieve in this setting. Moreover, our scheme makes only black box use of the underlying public-key encryption scheme. We note that even constructing optimal public-key attribute-based encryption, a weaker form of FE, based on minimal assumptions was unknown prior to our work.
Private-Key Setting. In the private-key setting, a recent work of Chen, Vaikuntanathan, Waters, Wee and Wichs [CVW+18] showed how to achieve optimal bounded-key FE based on the assumption of learning with errors. Moreover, their scheme was only selectively secure. Thus, constructing optimal bounded-key FE in the private-key setting based on the minimal assumption of one-way functions was open.
We show,
Theorem 2 (Informal)
Assuming the existence of one-way functions, there exists a bounded-key private-key FE scheme for \(\mathsf {P}/\mathsf {Poly}\) with encryption complexity \(Q \cdot \mathsf {poly}(\lambda ,s)\), where Q is the collusion bound and s is the maximum size of the functions queried.
Our private-key scheme has the same attractive features as our public-key scheme, that is, our private-key scheme satisfies simulation security, adaptive security and only makes black-box use of the underlying cryptographic primitive.
Dichotomy in Bounded-Key Functional Encryption. We see our work as establishing a dichotomy in bounded-key functional encryption (in both public-key and private-key settings): (i) for any constant \(\varepsilon > 0\), any bounded-key FE scheme with encryption complexity \(Q^{1-\varepsilon } \mathrm {poly}(\lambda ,s)\) implies indistinguishability obfuscation and, (ii) the existence of bounded-key FE with encryption complexity \(Q \cdot \mathrm {poly} (\lambda ,s)\) can be based solely on minimal assumptions.
1.2 Prior Works on Bounded-Collusion FE
Dichotomy in Bounded-Key IBE. Early work by Dodis, Katz, Xu and Yung [DKXY02] showed how to construct a Q-bounded identity-based encryption (IBE) scheme, another special case of FE, where the public parameters had size \(O(Q^2\lambda )\), and the ciphertexts and secret keys had size \(O(Q\lambda )\), starting from any public-key encryption scheme. Goldwasser, Lewko and Wilson [GLW12] later showed a construction with public parameters of size \(O(Q\lambda )\), and ciphertexts and secret keys of size \(O(\lambda )\), albeit under more structured algebraic assumptions.
More recently, Döttling and Garg [DG17b] and followup works [BLSV18, DG17a] showed how to bootstrap any bounded collusion IBE with public parameters of size \(Q^{1-\epsilon }\cdot \mathsf {poly}(\lambda )\), irrespective of ciphertext and secret-key length, into a full-fledged (i.e., fully collusion-resistant) IBE scheme.
This gives us a dichotomy for IBE: Q-bounded IBE with public parameters of size \(\varOmega (Q)\) exists under the minimal assumption of public-key encryption; and doing any better in terms of the size of public parameters is as hard as achieving unbounded-collusion IBE.
Bounded-Key FE. In the other extreme, the situation with general functional encryption (FE) is less clear-cut. The first construction of bounded-key FE for Boolean functionsFootnote 1 in \(\mathsf {NC}^1\) was demonstrated by Gorbunov, Vaikuntanathan and Wee [GVW12a], who built on the work of Sahai and Seyalioglu [SS10]; the encryption complexity in their scheme was \(Q^4\cdot \mathsf {poly}(\lambda ,s)\). They also showed how to extend this to support all poly-time computable functions, but at the expense of an additional assumption, namely pseudorandom functions that can be computed in \(\mathsf {NC}^1\), an object that we currently know how to construct based only on algebraic assumptions such as factoring, DDH and LWE. (see Fig. 1 for a detailed comparison.) Agrawal and Rosen [AR17] showed how to reduce the ciphertext size to \(Q^2 + \mathsf {poly}(\lambda ,s)\) under the LWE assumption. Chen, Vaikuntanathan, Waters, Wee and Wichs [CVW+18] very recently showed how to reduce the dependence even further to \(Q\cdot \mathsf {poly}(\lambda ,d)\) under the LWE assumption, except they could only achieve private-key FE. The ciphertext size dependence on Q in this last result is the best possible (without constructing IO) except that (a) they rely on LWE; and (b) they only achieve private-key FE. Even in the much weaker setting of public-key attribute-based encryption (ABE), the best known ciphertext size is \(Q^2\cdot \mathsf {poly}(\lambda ,s)\) in constructions that rely only on public-key encryption [ISV+17].
Dependence on the Circuit Size. We do caution the reader that our focus will be on the dependence of the ciphertext size on the collusion-bound Q. Ciphertexts in our scheme grow with the circuit-size of the functions that the scheme supports (denoted s in Fig. 1). On the one hand, for constructions that rely only on the minimal assumption of public-key encryption, this dependence seems hard to remove; indeed, even the best 1-bounded FE with ciphertext size sublinear in the circuit-size of the (Boolean) functions assumes (subexponential) LWE [GKP+13]. On the other hand, we show how to translate any improvement in this state of affairs for 1-bounded FE into a corresponding improvement in Q-bounded FE with ciphertexts that grow linearly in the collusion bound Q. Concretely, applying our techniques to the 1-bounded FE of [GKP+13] gives us a Q-bounded FE from subexponential LWE where ciphertexts grow as \(Q\cdot \mathsf {poly}(\lambda ,d)\) where d is the circuit-depth, improving on [AR17] (who achieve a quadratic dependence in Q) and on [CVW+18] (who construct a private-key FE scheme with a linear dependence in Q).
1.3 Technical Overview
We give an overview of the techniques. For the current discussion, our focus will be on the public-key setting; the techniques carry over mutatis mutandis to the private-key setting as well. We show our result in two steps. In the first step, we construct a public-key bounded-key FE for \(\mathsf {P}/\mathsf {Poly}\) starting from any public-key encryption scheme. We will not worry about optimizing the ciphertext size; indeed, it will be a large polynomial in the collusion bound Q. In the second step, we show a general way to reduce the ciphertext size: we show how to transform an FE scheme, where the ciphertext complexity grows polynomial in the collusion bound, into a FE scheme with linear complexity.
We now describe an overview of the techniques involved in the two steps, in order. In the technical sections, we invert the order of presentation since the second step (see Sect. 4) is simpler than the first (see Sect. 5).
First Step: Bounded-Key FE for \(\mathsf {P}/\mathsf {Poly}\). Our starting point is the observation from [SS10, GVW12a] that secure multiparty computation protocols with certain properties can be used to construct FE schemes; for [SS10], it was Yao’s two-party computation protocol [Yao86] and for [GVW12a], it was a non-interactive version of the BGW multi-party protocol [BOGW88]. Broadly speaking, our goal in this paper is to identify the right notion of MPC that can be turned into optimal bounded-collusion FE.
Towards this end, we define secure multiparty computation protocols in a client-server framework where there is a single client who wishes to delegate an a-priori bounded number Q of computations to N servers. We first describe the syntax of such protocols and then the security we require of them. A protocol in the client-server framework proceeds in two phases:
-
An offline phase where the client encodes a private input x into N encodings, and the \(i^{th}\) server gets the \(i^{th}\) encoding.
-
An online phase which is executed Q times, once for every function that the client wishes to delegate. In the \(j^{th}\) session, the client encodes a circuit \(C_j\) into N encodings, and sends each server an encoding. At this stage, only n of the N servers come online, perform some local computation on their encodings, and output a single message each. (We call the local computation function \(\mathsf {Local}\).) A public decoding algorithm can then reconstruct the value \(C_j(x)\) from these server messages. (We call the reconstruction function \(\mathsf {Decode}\).) Crucially, we require that the client does not keep any shared state between the online and offline phases.
As for security, we consider an adversary that corrupts an arbitrary size-t subset of the servers (for some pre-determined t) and learns (a) the offline phase messages received by these t servers and (b) the messages of all the servers in the online phase; that is, the adversary gets to see the entire communication between the client and the servers in the online phase. We require that such an adversary does not learn anything more about the client input x other than \(\{C_j(x)\}_{j\in [Q]}\). This requirement is captured through a simulation-based definition. Two aspects make it challenging to construct such protocols:
-
Reusability: the input encodings generated by the client should be reusable across different computations; and
-
Dynamic Recovery: the ability for only a subset of servers to come together in the online phase to recover the output.
For the current discussion, we call secure protocols that satisfy both the above properties as reusable dynamic MPC protocols. In the technical sections, we will not explicitly use the terminology of reusable dynamic MPC protocols and just refer to them as client-server protocols.
Implicit in [GVW12a] is a construction of a reusable dynamic MPC protocol, where the circuits delegated by the client are in \(\mathsf {NC}^1\). There is a fundamental barrier in extending their approach to handle circuits in \(\mathsf {P}/\mathsf {Poly}\) as they crucially use a two-round MPC protocol (derived from BGW) that securely computes polynomials. Circuits in \(\mathsf {P}/\mathsf {Poly}\) are believed to not have efficient polynomial representations. While several recent works [BL18, GS18, ACGJ18, GIS18, ABT18] demonstrate two-round MPC protocols that securely compute \(\mathsf {P}/\mathsf {Poly}\), they fail to simultaneously satisfy reusability and dynamic recovery. Nonetheless, we will crucially use the construction of reusable dynamic MPC protocol for \(\mathsf {NC}^1\) [GVW12a], denoted by \(\varPi _{\mathsf {NC}^1}\), to build a protocol for \(\mathsf {P}/\mathsf {Poly}\).
From Client-Server Protocol for \(\mathsf {P}/\mathsf {Poly}\) to Bounded-Key FE for \(\mathsf {P}/\mathsf {Poly}\). Before we construct reusable dynamic MPC protocols for \(\mathsf {P}/\mathsf {Poly}\), we first show how such protocols are useful in obtaining bounded-collusion FE for \(\mathsf {P}/\mathsf {Poly}\). As an intermediate tool, we use a single-key FE scheme for \(\mathsf {P}/\mathsf {Poly}\). This is a well studied object and can be based solely on the existence of public-key encryption [SS10]. We call such a scheme \(\mathsf {1fe}\) and we denote the bounded-collusion FE scheme that we wish to construct to be \(\mathsf {BFE}\). The construction of \(\mathsf {BFE}\), which follows along the lines of [GVW12a], proceeds as follows:
-
The setup of \(\mathsf {BFE}\) invokes \(N=\mathrm {poly}(Q)\) instantiations of \(\mathsf {1fe}\). The N public keys of \(\mathsf {1fe}\) form the master public key of \(\mathsf {BFE}\) and similarly the N secret keys of \(\mathsf {1fe}\) form the master secret key of \(\mathsf {BFE}\).
-
To encrypt an input x in \(\mathsf {BFE}\), run the offline phase of the client-server framework. Denote the output to be \((\widehat{x}^1,\ldots ,\widehat{x}^N)\). Encrypt \(\widehat{x}^\mathbf{u }\) under the \(\mathbf u ^{th}\) instantiation of \(\mathsf {1fe}\). Output all the N ciphertexts of \(\mathsf {1fe}\).
-
The key generation for a circuit C in \(\mathsf {BFE}\) is done as follows: run the client delegation procedure \(\mathsf {CktEnc}\) on C to obtain \((\widehat{C}^1,\ldots ,\widehat{C}^N)\). Pick a random n-sized subset \(\mathbf {S}\subseteq [N]\) and generate \(\mathsf {1fe}\) functional keys for \(\mathsf {Local}(\widehat{C}^\mathbf{u },\cdot )\) (recall that \(\mathsf {Local}\) is part of the online phase in client-server framework) for every \(\mathbf u \) in the set \(\mathbf {S}\). Output all the n functional keys of \(\mathsf {1fe}\).
Note that here we crucially use the fact that the client does not share state between the offline and online phases.
-
The decryption proceeds by first decrypting the \(\mathbf u ^{th}\) ciphertext of \(\mathsf {1fe}\) using the \(\mathbf u ^{th}\) functional key to obtain the encoding \(\widehat{y}^\mathbf{u }\). Then run \(\mathsf {Decode}\) to recover the answer.
The correctness of \(\mathsf {BFE}\) follows from the correctness guarantees of \(\mathsf {1fe}\) and the reusable dynamic MPC framework. To argue security, as in [GVW12a], a simple combinatorial argument is first invoked to prove that the size of pairwise intersections of the sets chosen during the key-generation procedures of all the Q functional keys is at most t. For this argument to work, we need to set N to be a sufficiently large polynomial in Q. Using this observation, we can deduce that at most t instantiations of \(\mathsf {1fe}\) can be rendered insecure. An \(\mathsf {1fe}\) instantiation being rendered insecure means that the corresponding server is corrupted in the client-server framework; note that there is a one-to-one correspondence between the number of instantiations of \(\mathsf {1fe}\) and the number of servers in the client-server framework. We can then use the property that the client-server protocol is secure even if at most t servers are corrupted, to argue that the scheme \(\mathsf {BFE}\) is secure.
Moreover, since \(\mathsf {1fe}\) can be based on public-key encryption (resp., one-way functions), we obtain a public-key (resp., secret-key) \(\mathsf {BFE}\) for \(\mathsf {P}/\mathsf {Poly}\) from reusable dynamic MPC for \(\mathsf {P}/\mathsf {Poly}\) assuming only public-key encryption (resp., one-way functions).
Reusable Dynamic MPC Protocol for \(\mathsf {P}/\mathsf {Poly}\). Now that we have shown that reusable dynamic MPC is useful for constructing bounded-key FE, we shift our focus to building this object.
Towards this, we first define the abstraction of correlated garbling. This abstraction allows for generating multiple garbled circuits from a shared random string. More specifically, it comprises of two algorithms: \(\mathsf {CorrGarb}\) and \(\mathsf {CorrEval}\). The correlated garbling algorithm \(\mathsf {CorrGarb}\) takes as input circuit C, input x, a random string R (not necessarily uniformly generated) and outputs a garbled circuit \(\mathsf {GC}\) and appropriate wire labels \(\mathbf {K}_x\). The evaluation algorithm \(\mathsf {CorrEval}\) takes as input \((\mathsf {GC},\mathbf {K}_x)\) and outputs C(x). We require that all the different correlated garbled circuits \(\{\mathsf {GC}_i \leftarrow \mathsf {CorrGarb}(C_i,x,R)\) produced using the same string R do not reveal any information about x beyond \(\{(C_i,C_i(x))\}\).
We use this abstraction to transform \(\varPi _{\mathsf {NC}^1}\) (recall, \(\varPi _{\mathsf {NC}^1}\) is a reusable dynamic protocol for \(\mathsf {NC}^1\)) into a reusable dynamic for \(\mathsf {P}/\mathsf {Poly}\) as follows:
-
Offline Phase: to encode an input x, generate a random string R (as dictated by correlated garbling) and then encode (x, R) using the offline phase of \(\varPi _{\mathsf {NC}^1}\) to obtain N input encodings.
-
Online Phase: in the \(i^{th}\) session, let \(C_i\) be the circuit delegated by the client. The client generates the online phase of \(\varPi _{\mathsf {NC}^1}\) on the circuit \(\mathsf {CorrGarb}(C_i,\cdot ,\cdot )\) to obtain N circuit encodings and sends one encoding to each of the servers. A subset of the servers perform local computation of \(\varPi _{\mathsf {NC}^1}\) and each of them output a single message. The value \(C_i(x)\) can be recovered from the outputs of the servers in two steps: (i) run the decoding procedure of \(\varPi _{\mathsf {NC}^1}\) to obtain the correlated garbled circuit-wire keys pair \((\mathsf {GC}_i,\mathbf {K}_{x}^i)\) of \((C_i,x)\) and then, (ii) run \(\mathsf {CorrEval}\) on the correlated garbled circuit to recover the answer.
In order to implement the above construction, it is required that \(\mathsf {CorrGarb}\) is representable by an \(\mathsf {NC}^1\) circuit: this is because \(\varPi _{\mathsf {NC}^1}\) only allows for delegating computations in \(\mathsf {NC}^1\). The security of the above construction follows from the fact that the different correlated garbled circuits along with wire keys \(\{(\mathsf {GC}_i,\mathbf {K}_x^i)\}\) can be simulated using \(\{(C_i,C_i(x))\}\): note that all the correlated garbled circuits are computed as a function of the same random string R. In Sect. 5, we give a direct construction of client-server protocol from correlated garbling; in particular we do not assume that a client-server protocol for \(\mathsf {NC}^1\) as implicitly proposed in [GVW12a].
All that remains is to construct a correlated garbling scheme with the garbling function in \(\mathsf {NC}^1\). We introduce novel techniques in this construction and this is the main technical contribution of the paper.
Construction of Correlated Garbling. The main hurdle in constructing a correlated garbling scheme is to ensure the security of different correlated garbled circuits computed using the same randomness. As a first attempt, we use the classical garbling scheme of Yao [Yao86]:
-
Let s be the number of wires in the circuit to be garbled. For every wire w in the circuit, generate a large (i.e., \(\mathrm {poly}(\lambda ,Q)\)) number of uniformly random keys, denoted by the vector \(\overrightarrow{\mathbf {K}_w^0}\), associated with bit 0 and \(\lambda \) number of keys \(\overrightarrow{\mathbf {K}_w^1}\) for bit 1. Similarly, for every gate G in the circuit, generate a large (i.e., \(\mathrm {poly}(\lambda ,Q)\)) number of random strings, denoted by \(\overrightarrow{\mathbf {R}_G}\). The collection of all the strings form the random string R that will be input to \(\mathsf {CorrGarb}\).
-
To garble a circuit C, \(\mathsf {CorrGarb}\) performs the following steps:
-
Generation of wire keys and randomness for encryption: It chooses a random \(\lambda \)-sized subset S; for every wire w, it generates the wire key \(K_w^0\) (resp., \(K_w^1\)) for w by XOR-ing the subset S of keys in \(\overrightarrow{\mathbf {K}_w^0}\) (resp., \(\overrightarrow{\mathbf {K}_w^1}\)). Similarly, generate \(R_G\) by XOR-ing the subset S of random strings in \(\overrightarrow{\mathbf {R}_G}\).
-
Generating the garbled gates: Using the wire keys and the random strings generated using the above process, we generate the garbled gates for every gate in the circuit. The generation process will be performed as described in [Yao86]. In particular, this process will employ a private-key encryption scheme to generate four ciphertexts associated with every gate in the circuit.
-
-
\(\mathsf {CorrEval}\) is the same as the evaluation algorithm of the garbling scheme by [Yao86].
In addition to security, we need to argue that \(\mathsf {CorrGarb}\) can be implemented in \(\mathsf {NC}^1\); recall that the latter property was crucially used to construct reusable dynamic MPC for \(\mathsf {P}/\mathsf {Poly}\). Let us first give intuition as to why the above template satisfies security.
Suppose the string R (input to \(\mathsf {CorrGarb}\)) is reused Q times to generate Q different collections of wire keys and random strings, with each such collection generated using a different random set S. Then each collection in turn is used to generate a single garbled circuit. First we invoke a combinatorial argument to prove that the joint distribution of the Q collections of wire keys and the random strings, generated as above, is identical to the product uniform distribution. Once this is proven, this proof can then be leveraged, using arguments standard in the garbling literature, to argue the security of the above correlated garbling candidate.
All is left is to show that \(\mathsf {CorrGarb}\) can be implemented in \(\mathsf {NC}^1\). Since the procedure \(\mathsf {CorrGarb}\) involves running the encryption algorithm of a private-key scheme, at the very least we need to start with a private-key scheme with encryption algorithm computable in \(\mathsf {NC}^1\). Unfortunately such schemes are known to exist only based on algebraic assumptions, in particular, assuming \(\mathsf {PRGs}\) in \(\mathsf {NC}^1\). Thus, the above candidate does not work for us.
To overcome this barrier, we make the following observation: notice that the generation of the random string R fed into \(\mathsf {CorrGarb}\) is “lightweight", meaning that no cryptographic primitives are used. On the other hand, the algorithm \(\mathsf {CorrGarb}\) is “crypto-heavy", meaning that it makes many invocations of a cryptographic primitive and specifically, a private-key encryption scheme. We design a flipped correlated garbling scheme, where the generation of R is “crypto-heavy" while \(\mathsf {CorrGarb}\) is “lightweight".
Specifically, we make the following changes to the above candidate.
-
Instead of invoking the \(\mathsf {PRG}\) during the execution of \(\mathsf {CorrGarb}\), we instead invoke this during the generation of R. While doing so, we observe that it is no longer necessary that \(\mathsf {PRG}\) needs to be computable in \(\mathsf {NC}^1\), since there is no such restriction when generating R. As a result, we will end up generating all the keys in \(\{\overrightarrow{\mathbf {K}_w^0},\overrightarrow{\mathbf {K}_w^1}\}\) using any pseudorandom generator.
-
To maintain correctness, we need to encrypt a subset of the seeds of the \(\mathsf {PRG}\) as part of the garbled table. Arguing security is more challenging now. We need to argue that the joint distribution of the Q collections of the wire keys and the random strings computed using R, is identical to the product uniform distribution, even if some of the \(\mathsf {PRG}\) seeds generating the wire keys are leaked and this step is crucial to the proof of the correlated garbling lemma.
The above template is an over-simplified presentation of correlated garbling and we refer the reader to the technical sections for a precise description.
Summarizing the First Step. We summarize the steps to construct a bounded-key functional encryption for \(\mathsf {P}/\mathsf {Poly}\).
-
1.
We construct correlated garbling for \(\mathsf {P}/\mathsf {Poly}\) from one-way functions.
-
2.
Combining correlated garbling with techniques from [GVW12a], we construct a protocol in the client-server framework (satisfying both reusability and dynamic recovery) that handles \(\mathsf {P}/\mathsf {Poly}\) computations.
-
3.
Finally, we construct bounded-key FE for \(\mathsf {P}/\mathsf {Poly}\) from a client-server protocol and single-key functional encryption for \(\mathsf {P}/\mathsf {Poly}\) [SS10, GVW12a].
The ciphertext complexity in the resulting FE scheme, however, grows polynomially in Q.
Second Step: Linear Dependence in Query Complexity. In the second step, we give a generic transformation to turn the FE scheme resulting from the first step into one that satisfies linear complexity property. This transformation is remarkably simple and draws connections to the classical load balancing problem. Recall in the load balancing problem, there are Q reviewers and there are Q papers to review, with each reviewer having bandwidth to review at most q papers. Assigning papers at random to the reviewers ensures that each reviewer has to review one paper on average. By a simple Chernoff argument coupled with union bound argument, it follows that, as long as q is large enough, the probability that any reviewer has to review more than q papers is small. We propose our transformation along these lines: let \(\mathsf {bfe}\) be the FE scheme obtained from the first step and let \(\mathsf {BFE}\) be the FE scheme with linear complexity that we wish to construct. To tolerate a query bound Q, we consider Q instantiations of \(\mathsf {bfe}\) in parallel, where the collusion bound (read as “load") in \(\mathsf {bfe}\) is set to be q.
-
To encrypt a message x in \(\mathsf {BFE}\), encrypt x in all the instantiations of \(\mathsf {bfe}\).
-
To generate a functional key for a circuit C, pick an index i in [Q] at random and generate a \(\mathsf {bfe}\) functional key corresponding to the \(i^{th}\) instantiation. This is akin to assigning a paper to a reviewer at random.
If we set q to be security parameter, we can prove (using Chernoff and union bounds) that it is highly unlikely that the number of \(\mathsf {bfe}\) functional keys issued for any given index is greater than q. This allows us to invoke the security of \(\mathsf {bfe}\) scheme to prove the security of \(\mathsf {BFE}\). Moreover, the ciphertext complexity of \(\mathsf {BFE}\) is linear in Q, as desired! (each \(\mathsf {bfe}\) ciphertext is of size fixed polynomial in the security parameter and in particular, independent of Q).
2 Preliminaries
We denote the security parameter by \(\lambda \). Suppose x and y be two strings. Then, we denote \(x \circ y\) to be the concatenation of x and y.
Let D be a distribution with an efficient sampler. We denote the process of sampling v from D to be \(v \xleftarrow {\$} D\). The statistical distance between two distributions \(D_0\) and \(D_1\) is \(\varepsilon \) if \(\sum _{v \in V}|\mathsf {Pr}[v \xleftarrow {\$} D_0] - \mathsf {Pr}[ v \xleftarrow {\$} D_1] | \le 2\varepsilon \), where V is the support of both \(D_0\) and \(D_1\). Two distributions \(D_0\) and \(D_1\) are computationally indistinguishable if for every probabilistic polynomial time (PPT) adversary \(\mathcal {A}\), the following holds: \(\left| \mathsf {Pr}_{v \xleftarrow {\$} D_0}[0 \leftarrow \mathcal {A}(v)] - \mathsf {Pr}_{v \xleftarrow {\$} D_1}[0 \leftarrow \mathcal {A}(v) ] \right| \le \mathsf {negl}(\lambda )\), for some negligible function \(\mathsf {negl}\).
We assume that without loss of generality, every polynomial-sized circuit considered in this work contain only boolean gates (over any universal basis) with at most two output wires. Note that if every gate in a polynomial-sized circuit has at most one output wire then this circuit is representable as a polynomial-sized formula and thus, is in \(\mathsf {NC}^1\). The class of all polynomial-sized circuits is denoted by \(\mathsf {P}/\mathsf {Poly}\).
2.1 Bounded-Key Functional Encryption
A public-key functional encryption scheme \(\mathsf {bfe}\) associated with a class of boolean circuits \(\mathcal {C}\) is defined by the following algorithms.
-
Setup, \(\mathsf {Setup}(1^{\lambda },1^Q,1^s)\): On input security parameter \(\lambda \), query bound Q, maximum size of the circuits s for which functional keys are issued, output the master secret key \(\mathsf {msk}\) and the master public key \(\mathsf {mpk}\).
-
Key Generation, \(\mathsf {KeyGen}(\mathsf {msk},C)\): On input master secret key \(\mathsf {msk}\) and a circuit \(C \in \mathcal {C}\), output the functional key \(\mathsf {sk}_{C}\).
-
Encryption, \(\mathsf {Enc}(\mathsf {mpk},x)\): On input master public key \(\mathsf {mpk}\), input x, output the ciphertext \(\mathsf {ct}\).
-
Decryption, \(\mathsf {Dec}(\mathsf {sk}_C,\mathsf {ct})\): On input functional key \(\mathsf {sk}_C\), ciphertext \(\mathsf {ct}\), output the value y.
Remark 1
A private-key functional encryption scheme is defined similarly, except that \(\mathsf {Setup}(1^{\lambda },1^Q,1^s)\) outputs only the master secret key \(\mathsf {msk}\) and the encryption algorithm \(\mathsf {Enc}\) takes as input the master secret key \(\mathsf {msk}\) and the message x.
Remark 2
Henceforth, \(\mathsf {Setup}\) will only take as input \((1^{\lambda },1^s)\) in the case when \(Q=1\).
A functional encryption scheme satisfies the following properties.
Correctness. Consider an input x and a circuit \(C \in \mathcal {C}\) of size s. We require the following to hold for every \(Q \ge 1\):
for some negligible function \(\mathsf {negl}\).
Efficiency. \(\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc}\) and \(\mathsf {Dec}\) run in time polynomial in their respective inputs.
We define a measure of efficiency that captures the dependance of the ciphertext complexity on the query bound. We define this formally below.
Definition 1 (Linear Complexity)
A functional encryption scheme \(\mathsf {bfe}=(\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})\) is said to have linear complexity if the following holds:
-
The time to compute \(\mathsf {Enc}(\mathsf {mpk},x)\) is \(Q \cdot \mathrm {poly}(\lambda ,s)\).
-
The time to compute \(\mathsf {KeyGen}(\mathsf {msk},C)\) for a circuit of size s is \(Q \cdot \mathrm {poly}(\lambda ,s)\).
where \((\mathsf {mpk},\mathsf {msk}) \leftarrow \mathsf {Setup}(1^{\lambda },1^Q,1^s)\).
Security. To define the security of a bounded-key functional encryption scheme \(\mathsf {bfe}\), we define two experiments \(\mathsf {Expt}_0\) and \(\mathsf {Expt}_1\). Experiment \(\mathsf {Expt}_0\), also referred to as real experiment, is parameterized by PPT stateful adversary \(\mathcal {A}\) and challenger \(\mathsf {Ch}\). Experiment \(\mathsf {Expt}_1\), also referred to as simulated experiment, is parameterized by PPT adversary \(\mathcal {A}\) and PPT stateful simulator \(\mathsf {Sim}\).
 :
:
-
\(\mathcal {A}\) outputs the query bound Q and the maximum circuit size s.
-
\(\mathsf {Ch}\) executes \(\mathsf {bfe}.\mathsf {Setup}(1^{\lambda },1^Q,1^s)\) to obtain the master public key-master secret key pair \((\mathsf {mpk},\mathsf {msk})\).
-
Circuit Queries: \(\mathcal {A}\), with oracle access to \(\mathsf {bfe}.\mathsf {KeyGen}(\mathsf {msk},\cdot )\), outputs the challenge message x.
-
Challenge Message Query: \(\mathsf {Ch}\) outputs the challenge ciphertext \(\mathsf {ct}\).
-
Circuit Queries: \(\mathcal {A}\), with oracle access to \(\mathsf {bfe}.\mathsf {KeyGen}(\mathsf {msk},\cdot )\), outputs the bit b.
-
If the total number of oracle calls made by \(\mathcal {A}\) is greater than Q, output \(\bot \). Otherwise, output b.
 :
:
-
\(\mathcal {A}\) outputs the query bound Q and the maximum circuit size s.
-
\(\mathsf {Sim}\), on input \((1^{\lambda },1^Q,1^s)\), outputs the master public key \(\mathsf {mpk}\).
-
Circuit Queries: \(\mathcal {A}\), with oracle access to \(\mathsf {Sim}\) (generating simulated functional keys), outputs the challenge message x.
-
Let \(\mathsf {QSet}\) be the set of circuit queries made by \(\mathcal {A}\) to \(\mathsf {Sim}\).
-
Construct the set \(\mathcal {V}\) as follows: for every \(C \in \mathsf {QSet}\), include (C, C(x)) in \(\mathcal {V}\).
-
-
Challenge Message Query: \(\mathsf {Sim}(1^{|x|},\mathcal {V})\) outputs the challenge ciphertext \(\mathsf {ct}\).
-
Circuit Queries: \(\mathcal {A}\), with oracle access to \(\mathsf {Sim}\) (generating simulated functional keys), outputs bit b.
-
If the total number of circuit queries made by \(\mathcal {A}\) is greater than Q, output \(\bot \). Otherwise, output b.
A public-key functional encryption scheme is adaptively secure if the output distributions of the above two experiments are computationally indistinguishable. More formally,
Definition 2 (Adaptive Security)
A public-key functional encryption scheme \(\mathsf {bfe}\) is adaptively secure if for every large enough security parameter \(\lambda \in \mathbb {N}\), every PPT adversary \(\mathcal {A}\), there exists a PPT simulator \(\mathsf {Sim}\) such that the following holds:
for some negligible function \(\mathsf {negl}\).
Remark 3
The selective security notion can be defined by similarly formulating the real and the simulated experiments. The only difference between selective security and adaptive security notions is that in the selective security notion, the adversary is supposed to output the challenge message even before it receives the master public key or makes any circuit query.
In the private-key setting, selective and adaptive security notions can be defined similarly.
3 Result Statements
We prove our result in two steps. In the first step, we present a transformation that converts a bounded-key functional encryption scheme, that doesn’t have linear complexity property, into one that satisfies linear complexity.
Generic Transformation to Achieve Linear Complexity. We prove the following theorem in Sect. 4.
Theorem 3
Consider a class \(\mathcal {C}\) of polynomial-sized circuits. If there exists a public-key (resp., private-key) bounded-key FE scheme for \(\mathcal {C}\) then there exists a public-key (resp., private-key) bounded-key FE scheme for \(\mathcal {C}\) that additionally satisfies linear complexity property (Definition 1).
Remark 4
Our transformation does not place any restrictions on \(\mathcal {C}\). In particular, our transformation works for identity-based encryption schemes, attribute-based encryption schemes, and so on.
The above theorem is restated as Theorem 6 in Sect. 4.
Bounded key FE for \(\mathsf {P}/\mathsf {Poly}\). We prove the following theorem in Sect. 5.
Theorem 4
Assuming the existence of public-key encryption (resp., one-way functions), there exists a public-key (resp., private-key) bounded-key functional encryption scheme for \(\mathsf {P}/\mathsf {Poly}\).
We prove the above theorem by first defining a client-server framework and then we construct a bounded-key FE from a client-server protocol. Finally, we instantiate client-server protocols from one-way functions.
The above theorem is restated as Theorem 7 in Sect. 5.
Bounded Key FE for \(\mathsf {P}/\mathsf {Poly}\) satisfying Linear Complexity. By combining the above two theorems, we achieve our main result.
Theorem 5 (Main Theorem)
Assuming the existence of public-key encryption (resp., one-way functions), there exists a public-key (resp., private-key) bounded-key functional encryption scheme satisfying linear complexity property for \(\mathsf {P}/\mathsf {Poly}\).
Our construction of functional encryption scheme in the above theorem makes only black box use of public-key encryption (or one-way functions).
4 Achieving Linear Complexity Generically
We show how to generically achieve linear complexity for any bounded-key FE scheme. In particular, we prove the following:
Theorem 6
If there exists a bounded-key FE scheme, denoted by \(\mathsf {bfe}\), for \(\mathcal {C}\) then there exists a bounded-key FE scheme, denoted by \(\mathsf {BFE}\), for \(\mathcal {C}\) that additionally satisfies linear complexity property (Definition 1). Moreover, the following holds:
-
If \(\mathsf {bfe}\) is adaptively secure (resp., selectively secure) then \(\mathsf {BFE}\) is adaptively secure (resp., selectively secure).
-
If \(\mathsf {bfe}\) is a public-key (resp., private key) scheme then \(\mathsf {BFE}\) is a public-key (resp., private key) scheme.
-
If \(\mathsf {bfe}\) is simulation secure (resp., IND-secure) then \(\mathsf {BFE}\) is simulation secure (resp., IND-secure).
Proof
We focus on the case when \(\mathsf {bfe}\) is adaptively secure, public-key and simulation secure. Our construction easily extends to the other cases as well.
We describe \(\mathsf {BFE}\) below.
-
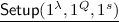 : On input security parameter \(\lambda \), query bound Q, maximum circuit size s for which functional keys are issued, generate \((\mathsf {mpk}_i,\mathsf {msk}_i) \leftarrow \mathsf {bfe}.\mathsf {Setup}(1^{\lambda },1^q,1^s)\) for every \(i \in [Q]\), where \(q=\lambda \) (in fact, q can even be set to be poly-logarithmic in the security parameter). Output the following: $$\mathsf {MSK}=\left( \mathsf {msk}_1,\ldots ,\mathsf {msk}_{Q} \right) ,\ \mathsf {MPK}=\left( \mathsf {mpk}_1,\ldots ,\mathsf {mpk}_{Q} \right) $$
: On input security parameter \(\lambda \), query bound Q, maximum circuit size s for which functional keys are issued, generate \((\mathsf {mpk}_i,\mathsf {msk}_i) \leftarrow \mathsf {bfe}.\mathsf {Setup}(1^{\lambda },1^q,1^s)\) for every \(i \in [Q]\), where \(q=\lambda \) (in fact, q can even be set to be poly-logarithmic in the security parameter). Output the following: $$\mathsf {MSK}=\left( \mathsf {msk}_1,\ldots ,\mathsf {msk}_{Q} \right) ,\ \mathsf {MPK}=\left( \mathsf {mpk}_1,\ldots ,\mathsf {mpk}_{Q} \right) $$ -
 : On input master secret key \(\mathsf {msk}\), circuit \(C \in \mathcal {C}\),
: On input master secret key \(\mathsf {msk}\), circuit \(C \in \mathcal {C}\),-
Sample \(\mathbf u \xleftarrow {\$} [Q]\).
-
Generate \(\mathsf {sk}_{C} \xleftarrow {\$} \mathsf {bfe}.\mathsf {KeyGen}(\mathsf {bfe}.\mathsf {msk}_\mathbf{u },C)\).
Output \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\).
-
-
 : On input master public key \(\mathsf {MPK}\), input x, generate \(\mathsf {ct}_i \leftarrow \mathsf {bfe}.\mathsf {Enc}(\mathsf {mpk}_i,x)\) for every \(i \in [Q]\). Output \(\mathsf {CT}=(\mathsf {ct}_1,\ldots ,\mathsf {ct}_{Q})\).
: On input master public key \(\mathsf {MPK}\), input x, generate \(\mathsf {ct}_i \leftarrow \mathsf {bfe}.\mathsf {Enc}(\mathsf {mpk}_i,x)\) for every \(i \in [Q]\). Output \(\mathsf {CT}=(\mathsf {ct}_1,\ldots ,\mathsf {ct}_{Q})\). -
 : On input functional key \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\), ciphertext \(\mathsf {CT}=(\mathsf {ct}_1,\ldots ,\mathsf {ct}_Q)\), compute \(\mathsf {bfe}.\mathsf {Dec}(\mathsf {sk}_C,\mathsf {ct}_\mathbf{u })\). Output the result.
: On input functional key \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\), ciphertext \(\mathsf {CT}=(\mathsf {ct}_1,\ldots ,\mathsf {ct}_Q)\), compute \(\mathsf {bfe}.\mathsf {Dec}(\mathsf {sk}_C,\mathsf {ct}_\mathbf{u })\). Output the result.
The correctness of \(\mathsf {BFE}\) follows directly from the correctness of \(\mathsf {bfe}\). We analyze the efficiency of the above scheme next.
Suppose the time taken to generate a \(\mathsf {bfe}\) ciphertext of message x is \(\mathrm {poly}(\lambda ,s)\) then the time taken to generate a \(\mathsf {BFE}\) ciphertext of message x is \(Q \cdot \mathrm {poly}(\lambda ,s)\). Similarly, if the time taken to generate a \(\mathsf {bfe}\) functional key of C is \(\mathrm {poly}(\lambda ,s)\), where s is the size of C, then the time taken to generate a \(\mathsf {BFE}\) functional key of f is \(Q \cdot \mathrm {poly}(\lambda ,s)\). Thus, the resulting scheme \(\mathsf {BFE}\) satisfies linear complexity property.
The only property left to be proved is the security property, which we prove next.
Security. Let \(\mathsf {sim}\) be the stateful simulator of the \(\mathsf {bfe}\) scheme. Since we invoke \(\mathsf {bfe}\) scheme Q times in the scheme, we consider Q instantiations of the stateful simulator, denoted by \(\mathsf {sim}_1,\ldots ,\mathsf {sim}_Q\). We construct a simulator \(\mathsf {SIM}\) associated with the \(\mathsf {BFE}\) scheme. We denote the PPT adversary to be \(\mathcal {A}\).
The simulator \(\mathsf {SIM}\) proceeds as follows:
-
1.
It receives the query bound Q and the maximum circuit size s from \(\mathcal {A}\).
-
2.
For every \(i \in [Q]\), execute \(\mathsf {sim}_i(1^{\lambda },1^Q,1^s)\) to obtain the \(i^{th}\) master public key \(\mathsf {mpk}_i\). Set \(\mathsf {MPK}=(\mathsf {mpk}_1,\ldots ,\mathsf {mpk}_Q)\). Send \(\mathsf {MPK}\) to \(\mathcal {A}\).
-
3.
Initialize the sets \(\mathsf {qset}_i=\emptyset \), for every \(i \in [Q]\). For every circuit query C made by \(\mathcal {A}\), do the following:
Sample \(\mathbf u \xleftarrow {\$} [Q]\) and then generate \(\mathsf {sk}_{C} \leftarrow \mathsf {sim}_\mathbf{u }(C)\). Add C to \(\mathsf {qset}_\mathbf{u }\). If \(|\mathsf {qset}_\mathbf{u }| > q\) then output \(\bot \). Otherwise, send \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\).
\(\mathcal {A}\) finally outputs the challenge message x.
-
4.
For every \(i \in [Q]\), construct the set \(\mathcal {V}_i\) as follows: for every \(C \in \mathsf {qset}_i\), include (C, C(x)) in \(\mathcal {V}_i\). For every \(i \in [Q]\), compute \(\mathsf {sim}_{i}(1^{|x|},\mathcal {V}_i)\) to obtain \(\mathsf {ct}_i\). Set \(\mathsf {CT}=(\mathsf {ct}_1,\ldots ,\mathsf {ct}_Q)\). Send \(\mathsf {CT}\) to \(\mathcal {A}\).
-
5.
In the next phase, \(\mathcal {A}\) makes circuit queries. For every circuit query C made by the adversary, do the following:
Sample \(\mathbf u \xleftarrow {\$} [Q]\) and then generate \(\mathsf {sk}_{C} \leftarrow \mathsf {sim}_\mathbf{u }(C,C(x))\). Add C to \(\mathsf {qset}_\mathbf{u }\). If \(|\mathsf {qset}_\mathbf{u }| > q\) then output \(\bot \). Otherwise, send \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\).
Consider the following hybrids. The changes are marked in
 .
.
 : This corresponds to the real experiment. For completeness, we describe the real experiment here.
: This corresponds to the real experiment. For completeness, we describe the real experiment here.
-
1.
The challenger \(\mathsf {Ch}\) receives the query bound Q and the maximum circuit size s from \(\mathcal {A}\).
-
2.
Execute \(\mathsf {bfe}.\mathsf {Setup}(1^{\lambda },1^Q,1^s)\) for Q times to obtain \(\{(\mathsf {msk}_i,\mathsf {mpk}_i)\}_{i \in [Q]}\). Set \(\mathsf {MPK}=(\mathsf {mpk}_1,\ldots ,\mathsf {mpk}_Q)\). Send \(\mathsf {MPK}\) to \(\mathcal {A}\).
-
3.
Initialize the sets \(\mathsf {qset}_i=\emptyset \), for every \(i \in [Q]\). For every circuit query C made by \(\mathcal {A}\), \(\mathsf {Ch}\) does the following:
Sample \(\mathbf u \xleftarrow {\$} [Q]\) and then generate \(\mathsf {sk}_{C} \leftarrow \mathsf {bfe}.\mathsf {KeyGen}(\mathsf {msk}_\mathbf{u },C)\). Add C to \(\mathsf {qset}_\mathbf{u }\). Send \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\) to \(\mathcal {A}\). \(\mathcal {A}\) finally outputs the challenge message x.
-
4.
For every \(i \in [Q]\), generate \(\mathsf {ct}_i \leftarrow \mathsf {bfe}.\mathsf {Enc}(\mathsf {mpk}_i,x)\). Set \(\mathsf {CT}=(\mathsf {ct}_1,\ldots ,\mathsf {ct}_Q)\). Send \(\mathsf {CT}\) to \(\mathcal {A}\).
-
5.
In the next phase, \(\mathcal {A}\) makes circuit queries. For every circuit query C made by \(\mathcal {A}\), do the following:
Sample \(\mathbf u \xleftarrow {\$} [Q]\) and then generate \(\mathsf {sk}_{C} \leftarrow \mathsf {bfe}.\mathsf {KeyGen}(\mathsf {msk}_\mathbf{u },C)\). Add C to \(\mathsf {qset}_\mathbf{u }\). Send \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\) to \(\mathcal {A}\).
-
6.
Let b be the output of \(\mathcal {A}\). If \(\left| \bigcup _{i=1}^Q \mathsf {qset}_{i} \right| > Q\), output \(\bot \). Otherwise, output b.
Remark 5
Note that the experiment described above is phrased differently from the real experiment of the bounded-key FE scheme. In the real experiment, the challenger only keeps track of the total number of \(\mathsf {BFE}\) circuit queries made by the adversary but in \(\mathbf {Hyb}_1\), the challenger keeps track of the set of \(\mathsf {bfe}\) functional keys issued per index. Since ultimately the challenger only aborts if the size of the union of all these sets exceeds Q, the output distribution of \(\mathbf {Hyb}_1\) is the same as the output distribution of the real experiment.
 : This hybrid is the same as the previous hybrid except that the real experiment outputs \(\bot \) if there exists an index \(\mathbf u \in [Q]\) such that \(|\mathsf {qset}_\mathbf{u }| > q\).
: This hybrid is the same as the previous hybrid except that the real experiment outputs \(\bot \) if there exists an index \(\mathbf u \in [Q]\) such that \(|\mathsf {qset}_\mathbf{u }| > q\).
In particular, we make the following changes to bullets 3 and 5 in the experiment described in \(\mathbf {Hyb}_1\).
-
3.
Initialize the sets \(\mathsf {qset}_i=\emptyset \), for every \(i \in [Q]\). For every circuit query C made by \(\mathcal {A}\), \(\mathsf {Ch}\) does the following:
Sample \(\mathbf u \xleftarrow {\$} [Q]\) and then generate \(\mathsf {sk}_{C} \leftarrow \mathsf {bfe}.\mathsf {KeyGen}(\mathsf {msk}_\mathbf{u },C)\). Add C to \(\mathsf {qset}_\mathbf{u }\).
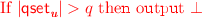 . Otherwise, send \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\) to \(\mathcal {A}\).
. Otherwise, send \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\) to \(\mathcal {A}\).\(\mathcal {A}\) finally outputs the challenge message x.
-
5.
In the next phase, \(\mathcal {A}\) makes circuit queries. For every circuit query C made by \(\mathcal {A}\), do the following:
Sample \(\mathbf u \xleftarrow {\$} [Q]\) and then generate \(\mathsf {sk}_{C} \leftarrow \mathsf {bfe}.\mathsf {KeyGen}(\mathsf {msk}_\mathbf{u },C)\). Add C to \(\mathsf {qset}_\mathbf{u }\).
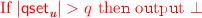 . Otherwise, send \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\) to \(\mathcal {A}\).
. Otherwise, send \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\) to \(\mathcal {A}\).
Claim
The statistical distance between the output distributions of \(\mathbf {Hyb}_1\) and \(\mathbf {Hyb}_2\) is at most \(Q \cdot e^{-\frac{(q-1)^2}{1+q}}\) and thus, negligible in \(\lambda \).
Proof
Define \(\mathbf {X}_\mathbf{u ,j}\), for every \(\mathbf u \in [Q],j \in [Q]\), to be a random variable such that \(\mathbf {X}_\mathbf{u ,j}=1\) if in the \(j^{th}\) circuit query C made by the adversary, the challenger responds with \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\); that is, the challenger responds with the functional key corresponding to the \(\mathbf u ^{th}\) instantiation of \(\mathsf {bfe}\). Let \(\mathbf {X}_\mathbf{u }=\sum _{j=1}^Q \mathbf {X}_\mathbf{u ,j}\).
Note that \(\mathsf {Pr}[\mathbf {X}_\mathbf{u ,j}=1]=\frac{1}{Q}\). By linearity of expectation, \(\mathbb {E}\left[ \mathbf {X}_\mathbf{u } \right] =1\).
By Chernoff bound, we have the following: for every \(\mathbf u \in Q\),
Thus for any fixed \(\mathbf u \in [Q]\), the probability that the number of \(\mathsf {bfe}\) functional keys per index \(\mathbf u \) issued by the challenger is greater than q is at most \(e^{-\frac{(q-1)^2}{1+q}}\). By union bound, the probability that there exists an index \(\mathbf u \) such that the challenger issues more than q functional keys with respect to \(\mathbf u \) is at most \(Q \cdot e^{-\frac{(q-1)^2}{1+q}}\).
Next, we consider a sequence of intermediate hybrids.
 : In this intermediate hybrid, the first \(\mathbf u \) instantiations, with \(\mathbf u < \mathbf {j}\) are simulated. The rest of the instantiations are honestly computed.
: In this intermediate hybrid, the first \(\mathbf u \) instantiations, with \(\mathbf u < \mathbf {j}\) are simulated. The rest of the instantiations are honestly computed.
We consider \(\mathbf {j}\) instantiations of the stateful simulator, denoted by \(\mathsf {sim}_1,\ldots ,\mathsf {sim}_{\mathbf {j}}\). We describe the hybrid experiment below.
-
1.
The challenger \(\mathsf {Ch}\) receives the query bound Q and the maximum circuit size s from \(\mathcal {A}\).
-
2.
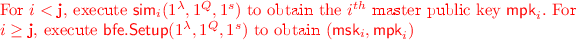 . Set \(\mathsf {MPK}=(\mathsf {mpk}_1,\ldots ,\mathsf {mpk}_Q)\). Send \(\mathsf {MPK}\) to \(\mathcal {A}\).
. Set \(\mathsf {MPK}=(\mathsf {mpk}_1,\ldots ,\mathsf {mpk}_Q)\). Send \(\mathsf {MPK}\) to \(\mathcal {A}\). -
3.
Initialize the sets \(\mathsf {qset}_i=\emptyset \), for every \(i \in [Q]\). For every circuit query C made by \(\mathcal {A}\), \(\mathsf {Ch}\) does the following: Sample \(\mathbf u \xleftarrow {\$} [Q]\) and then generate \(\mathsf {sk}_C\) as follows:
-
 .
. -
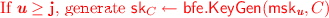 .
.
Add C to \(\mathsf {qset}_\mathbf{u }\). If \(|\mathsf {qset}_\mathbf{u }| > q\) then output \(\bot \). Otherwise, send \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\) to \(\mathcal {A}\). \(\mathcal {A}\) finally outputs the challenge message x.
-
-
4.
For every \(i \in [Q]\), construct the set \(\mathcal {V}_i\) as follows: for every \(C \in \mathsf {qset}_i\), include (C, C(x)) in \(\mathcal {V}_i\). Compute \(\mathsf {CT}\) as follows:
-
 .
. -
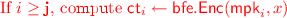 .
.
Set \(\mathsf {CT}=(\mathsf {ct}_1,\ldots ,\mathsf {ct}_Q)\). Send \(\mathsf {CT}\) to \(\mathcal {A}\).
-
-
5.
In the next phase, \(\mathcal {A}\) makes circuit queries. For every circuit query C made by \(\mathcal {A}\), do the following: Sample \(\mathbf u \xleftarrow {\$} [Q]\) and then generate \(\mathsf {sk}_C\) as follows:
-
 .
. -
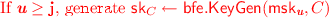 .
.
Add C to \(\mathsf {qset}_\mathbf{u }\). If \(|\mathsf {qset}_\mathbf{u }| > q\) then output \(\bot \). Otherwise, send \(\mathsf {SK}_C=(\mathbf u ,\mathsf {sk}_C)\) to \(\mathcal {A}\).
-
-
6.
Let b be the output of \(\mathcal {A}\). If \(\left| \bigcup _{i=1}^Q \mathsf {qset}_{i} \right| > Q\), output \(\bot \). Otherwise, output b.
The following two claims are immediate.
Claim
The output distributions of \(\mathbf {Hyb}_{2}\) and \(\mathbf {Hyb}_{3.1}\) are identically distributed.
Claim
For every \(\mathbf {j}\in [Q-1]\), the security of \(\mathsf {bfe}\) implies that the output distributions of \(\mathbf {Hyb}_{3.\mathbf {j}}\) and \(\mathbf {Hyb}_{3.\mathbf {j}+1}\) are computationally indistinguishable.
 : This corresponds to the simulated experiment.
: This corresponds to the simulated experiment.
The proof of the following claim is immediate.
Claim
The security of \(\mathsf {bfe}\) implies that the output distributions of \(\mathbf {Hyb}_{3.Q}\) and \(\mathbf {Hyb}_4\) are computationally indistinguishable.
5 Construction of Bounded-Key FE for \(\mathsf {P}/\mathsf {Poly}\)
We construct a bounded-key FE scheme for \(\mathsf {P}/\mathsf {Poly}\) as follows:
-
First we define a client-server framework and show how to construct a bounded-key FE for \(\mathsf {P}/\mathsf {Poly}\) from a protocol in this client-server framework.
-
We then show, in the full version [AV19], how to construct a protocol in the client-server framework from one-way functions.
We begin by describing the client-server framework.
5.1 Client-Server Framework
The client-server framework consists of a single client and \(N=N(\lambda ,Q)\) servers, where \(\lambda \) is the security parameter. It is additionally parameterized by \(n=n(\lambda ,Q)\) and \(t=t(\lambda ,Q)\). The framework consists of the following two phases:
-
Offline Phase: In this phase, the client takes as input the number of sessions Q, size of the circuit delegated s, input x and executes a PPT algorithm \(\mathsf {InpEnc}\) that outputs correlated input encodings \((\widehat{x}^1,\ldots ,\widehat{x}^N)\). It sends the encoding \(\widehat{x}^\mathbf{u }\) to the \(\mathbf{u }^{th}\) server.
-
Online Phase: This phase is executed for Q sessions. In each session, the client delegates the computation of a circuit C on x to the servers. This is done in the following steps:
-
Client Delegation: This is performed by the client computing a PPT algorithm \(\mathsf {CktEnc}\) on input \((1^{\lambda },1^Q,1^s,C)\) to obtain \((\widehat{C}^1,\ldots ,\widehat{C}^{N})\). It sends the circuit encoding \(\widehat{C}^\mathbf{u }\) to the \(\mathbf{u }^{th}\) server. Note that \(\mathsf {CktEnc}\) is executed independently of the offline phase and in particular, does not depend on the randomness used in the offline phaseFootnote 2.
-
Local Computation by Servers: Upon receiving the circuit encodings from the client, a subset \(\mathbf {S}\) of servers come online and the \(\mathbf{u }^{th}\) server in this set \(\mathbf {S}\) computes \(\mathsf {Local}(\widehat{C}^\mathbf{u },\widehat{x}^\mathbf{u })\) to obtain the \(\mathbf u ^{th}\) output encoding \(\widehat{y}^\mathbf{u }\).
-
Decoding: Finally, the output is recovered by computing a PPT algorithm \(\mathsf {Decode}\) on \(\left( \left\{ \widehat{y}^\mathbf{u } \right\} _\mathbf{u \in \mathbf {S}},\mathbf {S}\right) \).
-
We describe the properties below. We start with correctness.
Correctness. A protocol \(\varPi \) in the client-server framework is said to be correct if the following holds:
-
Suppose the client computes encodings of input x by computing \((\widehat{x}^1,\ldots ,\widehat{x}^N) \leftarrow \mathsf {InpEnc}(1^{\lambda },1^Q,1^s,x)\).
-
In the online phase, let C be the circuit that the client wants to delegate. The client computes \((\widehat{C}^1,\ldots ,\widehat{C}^N) \leftarrow \mathsf {CktEnc}(1^{\lambda },1^Q,1^s,C)\) and distributes the circuit encodings to all the servers. A subset of servers \(\mathbf {S}\subseteq [N]\), of size n, then locally compute on the circuit encodings. That is, for every \(\mathbf u \in \mathbf {S}\), the \(\mathbf u ^{th}\) server computes \(\widehat{y}^\mathbf{u } = \mathsf {Local}(\mathsf {gc},\widehat{x}^\mathbf{u })\). Finally, the output can be recovered by computing \(\mathsf {Decode}(\{\widehat{y}^\mathbf{u }\}_\mathbf{u \in \mathbf {S}},\mathbf {S})\) to obtain y.
We require that \(y=C(x)\).
Security. We allow the adversary to be able to corrupt a subset of servers. Once the server is corrupted, the entire state of the server is leaked to the adversary. The adversary, however, is not allowed to corrupt the client. In every session, since n servers can recover the output, the number of servers that can be corrupted has to be less than nFootnote 3.
Informally, we require the following guarantee: even if the adversary can corrupt a subset of servers, he cannot learn anything beyond the outputs of the computation \((C_1(x),\ldots ,C_Q(x))\) in every session, where \(C_1,\ldots ,C_Q\) are the circuits delegated by the client. However, the circuits \((C_1,\ldots ,C_Q)\) are not hidden from the adversary. Since our end goal is to build FE for \(\mathsf {P}/\mathsf {Poly}\), we need to suitably define the security property that would enable us to prove the security of FE. Towards this, we incorporate the following in the security definition of the client-server framework:
-
We not only allow the adversary to choose the servers to corrupt but also allow it to decide the subsets of servers \(\mathbf {S}_1,\ldots ,\mathbf {S}_Q\) participating in the Q sessions.
-
In every session, the adversary is provided all the N circuit encodings. Moreover, the outputs of the local computation of all the servers, including the honest servers, are visible to the adversary.
To define the security notion formally, we first state the following experiments. The first experiment \(\mathsf {Expt}_0\) is parameterized by a PPT adversary \(\mathcal {A}\) and PPT challenger \(\mathsf {Ch}\) and the second experiment \(\mathsf {Expt}_1\) is parameterized by \(\mathcal {A}\) and PPT stateful simulator \(\mathsf {Sim}_{\mathsf {csf}}\).
 :
:
-
\(\mathcal {A}\) outputs the query bound Q, maximum circuit size s, total number of parties N, number of parties n participating in any session, threshold t, corruption set \(\mathcal {S}_{\mathsf {corr}}\subseteq [N]\) and the input x. If \(|\mathcal {S}_{\mathsf {corr}}| > t\) then the experiment aborts. It also outputs the sets \(\mathbf {S}_1,\ldots ,\mathbf {S}_Q \subseteq [N]\) such that \(|\mathbf {S}_i|=n\), where \(\mathbf {S}_i\) is the set of parties participating in the \(i^{th}\) session.
-
Circuit Queries: \(\mathcal {A}\) is allowed to make a total of Q circuit queries. First, it makes \(Q_1 \le Q\) adaptiveFootnote 4 circuit queries \(C_1,\ldots ,C_{Q_1}\). For the \(i^{th}\) circuit query \(C_i\), \(\mathsf {Ch}\) computes \(\left( \widehat{C_i}^1,\ldots ,\widehat{C_i}^N \right) \leftarrow \mathsf {CktEnc}(1^{\lambda },1^Q,1^s,C_{i})\) and sends \( \left( \widehat{C_i}^1,\ldots ,\widehat{C_i}^N \right) \).
-
Challenge Input Query: \(\mathcal {A}\) submits the input x. \(\mathsf {Ch}\) generates \(\mathsf {InpEnc}(1^{\lambda },1^Q,1^s,x)\) to obtain \((\widehat{x}^1,\ldots ,\widehat{x}^N)\). \(\mathsf {Ch}\) sends \(\left( \{\widehat{x}^\mathbf{u }\}_\mathbf{u \in \mathcal {S}_{\mathsf {corr}}},\left\{ \mathsf {Local}\left( \widehat{C_i}^\mathbf{u },\widehat{x}^\mathbf{u } \right) \right\} _{i \in [Q_1],\mathbf u \in \mathbf {S}_{i}} \right) \). That is, the challenger sends the input encodings of the corrupted set of servers along with the outputs of \(\mathsf {Local}\) on the circuit encodings received so far.
-
Circuit Queries: \(\mathcal {A}\) then makes \(Q_2=Q-Q_1\) adaptive circuit queries \(C_{Q_1+1},\ldots ,C_{Q}\). \(\mathsf {Ch}\) computes \(\left( \widehat{C_{i}}^{1},\ldots ,\widehat{C_i}^{N} \right) \leftarrow \mathsf {CktEnc}(1^{\lambda },1^Q,1^s,C_{i})\) and sends \(\left\{ \left\{ \left( \widehat{C_{i}}^{1},\ldots ,\widehat{C_i}^{N} \right) ,\ \mathsf {Local}\left( \widehat{C_i}^\mathbf{u },\widehat{x}^\mathbf{u } \right) \right\} _{i \in \{Q_1+1,\ldots ,Q\},\mathbf u \in [\mathbf {S}_i]} \right\} \).
-
\(\mathcal {A}\) outputs a bit b. The output of the experiment is b.
 :
:
-
\(\mathcal {A}\) outputs the query bound Q, maximum circuit size s, total number of parties N, number of parties n participating in any session, threshold t, corruption set \(\mathcal {S}_{\mathsf {corr}}\subseteq [N]\) and the input x. If \(|\mathcal {S}_{\mathsf {corr}}| > t\) then the experiment aborts. It also outputs the sets \(\mathbf {S}_1,\ldots ,\mathbf {S}_Q \subseteq [N]\) such that \(|\mathbf {S}_i|=n\), where \(\mathbf {S}_i\) is the set of parties participating in the \(i^{th}\) session.
-
Circuit Queries: \(\mathcal {A}\) makes a total of Q adaptive queries. First it makes \(Q_1 \le Q\) adaptive circuit queries. For the \(i^{th}\) circuit query \(C_i\), the simulator computes \(\left( \widehat{C_i}^1,\ldots ,\widehat{C_i}^N \right) \leftarrow \mathsf {Sim}_{\mathsf {csf}}(C_{i})\) and sends \(\left( \widehat{C_i}^1,\ldots ,\widehat{C_i}^N \right) \).
-
Challenge Input Query: \(\mathcal {A}\) submits the input x. Construct \(\mathcal {V}\) as follows: \(\mathcal {V}=\{C_i,C_i(x): i \in [Q_1]\}\). \(\mathsf {Sim}_{\mathsf {csf}}\) on input \((1^{|x|},\mathcal {S}_{\mathsf {corr}},\mathcal {V})\) (and in particular, it does not get x as input) outputs the simulated encodings \((\{\widehat{x}^\mathbf{u }\}_\mathbf{u \in \mathcal {S}_{\mathsf {corr}}})\) and the encodings of outputs \(\left\{ \widehat{y}^\mathbf{u }_i \right\} _{i \in [Q_1],\mathbf u \in \mathbf {S}_{i}}\) such that \(\widehat{y}^\mathbf{u }_i=\mathsf {Local}\left( \widehat{C_i}^\mathbf{u },\widehat{x}^\mathbf{u } \right) \) for every \(\mathbf u \in \mathbf {S}_{i} \cap \mathcal {S}_{\mathsf {corr}}\).
-
Circuit Queries: \(\mathcal {A}\) then makes \(Q_2=Q-Q_1\) adaptive circuit queries \(C_{Q_1+1},\ldots ,C_{Q}\). The simulator \(\mathsf {Sim}_{\mathsf {csf}}\) on input \((i,C_{i},C_i(x))\), for \(i \in \{Q_1+1,\ldots ,Q\}\), sends \(\left( \left( \widehat{C_i}^1,\ldots ,\widehat{C_i}^N \right) ,\ \widehat{y}^\mathbf{u }_i \right) \).
-
\(\mathcal {A}\) outputs a bit b. The output of the experiment is b.
We formally define the security property below.
Definition 3 (Security)
A protocol \(\varPi \) is secure if for every PPT adversary \(\mathcal {A}\), there exists a PPT simulator \(\mathsf {Sim}_{\mathsf {csf}}\) such that the following holds:
for some negligible function \(\mathsf {negl}\).
5.2 Bounded-Key FE for \(\mathsf {P}/\mathsf {Poly}\) from Client-Server Framework
We now present a construction of a bounded-key functional encryption for all polynomial-sized circuits from a protocol in the client-server framework.
Theorem 7
There exists a public-key (resp., private-key) adaptively secure bounded-key functional encryption scheme \(\mathsf {BFE}\) for \(\mathsf {P}/\mathsf {Poly}\) assuming,
-
A public-key (resp., private-key) adaptively secure single-key functional encryption scheme \(\mathsf {1fe}\) for \(\mathsf {P}/\mathsf {Poly}\) and,
-
A protocol for \(\mathsf {P}/\mathsf {Poly}\) in the client-server framework, denoted by \(\varPi =(\mathsf {InpEnc},\mathsf {CktEnc},\mathsf {Local},\mathsf {Decode})\).
Proof
We focus on the public-key setting; the construction and the analysis for the private-key setting is identical. We describe the algorithms of \(\mathsf {BFE}\) below. Let the protocol in the client-server framework be parameterized by \(t=\varTheta (Q\lambda )\), \(N=\varTheta (Q^2t^2)\) and \(n=\varTheta (t)\), where Q is the query bound defined as part of the scheme.
-
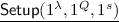 : On input security parameter \(\lambda \), query bound Q, circuit size s, generate \((\mathsf {msk}_{i},\mathsf {mpk}_i) \leftarrow \mathsf {1fe}.\mathsf {Setup}(1^{\lambda },1^s)\) for \(i \in [N]\). Output the following: $$\mathsf {MSK}=(\mathsf {msk}_1,\ldots ,\mathsf {msk}_N),\ \mathsf {MPK}=(Q,\ \mathsf {mpk}_1,\ldots ,\mathsf {mpk}_N)$$
: On input security parameter \(\lambda \), query bound Q, circuit size s, generate \((\mathsf {msk}_{i},\mathsf {mpk}_i) \leftarrow \mathsf {1fe}.\mathsf {Setup}(1^{\lambda },1^s)\) for \(i \in [N]\). Output the following: $$\mathsf {MSK}=(\mathsf {msk}_1,\ldots ,\mathsf {msk}_N),\ \mathsf {MPK}=(Q,\ \mathsf {mpk}_1,\ldots ,\mathsf {mpk}_N)$$ -
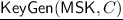 : On input master secret key \(\mathsf {MSK}\), circuit C,
: On input master secret key \(\mathsf {MSK}\), circuit C,-
Sample a set \(\mathbf {S}\xleftarrow {\$} [N]\), of size n, uniformly at random.
-
Compute \(\left( \widehat{C}^1,\ldots ,\widehat{C}^N \right) \leftarrow \mathsf {CktEnc}(1^{\lambda },1^Q,1^s,C)\).
-
Let \(\mathsf {E}^\mathbf{u }(\cdot ) = \mathsf {Local}(\widehat{C}^\mathbf{u },\cdot )\). Generate a functional key for \(\mathsf {E}^\mathbf{u }\); that is, compute \(\mathsf {sk}_{\mathsf {E}^\mathbf{u }} \leftarrow \mathsf {1fe}.\mathsf {KeyGen}(\mathsf {msk}_\mathbf{u },\mathsf {E}^\mathbf{u })\) for every \(\mathbf u \in \mathbf {S}\).
-
Output \(\mathsf {SK}_{C}=\left( \mathbf {S},\ \left\{ \mathsf {sk}_{\mathsf {E}^\mathbf{u }} \right\} _\mathbf{u \in \mathbf {S}} \right) \).
-
 : On input master public key \(\mathsf {MPK}\),
: On input master public key \(\mathsf {MPK}\),-
Compute \((\widehat{x}^{1},\ldots ,\widehat{x}^{N}) \leftarrow \mathsf {InpEnc}\left( 1^{\lambda },1^Q,1^s,x\right) \).
-
For every \(i \in [N]\), compute \(\mathsf {ct}_{i} \leftarrow \mathsf {FE}.\mathsf {Enc}\left( \mathsf {mpk}_{i},\widehat{x}^i\right) \).
-
Output \(\mathsf {CT}=(\mathsf {ct}_1,\ldots ,\mathsf {ct}_{N})\).
-
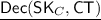 : On input functional key \(\mathsf {SK}_C=\left( \mathbf {S},\ \left\{ \mathsf {sk}_{\mathsf {E}^\mathbf{u }} \right\} _\mathbf{u \in \mathbf {S}} \right) \), ciphertext \(\mathsf {CT}=(\mathsf {ct}_1,\ldots ,\mathsf {ct}_{N})\),
: On input functional key \(\mathsf {SK}_C=\left( \mathbf {S},\ \left\{ \mathsf {sk}_{\mathsf {E}^\mathbf{u }} \right\} _\mathbf{u \in \mathbf {S}} \right) \), ciphertext \(\mathsf {CT}=(\mathsf {ct}_1,\ldots ,\mathsf {ct}_{N})\),-
For every \(\mathbf u \in \mathbf {S}\), compute \(\widehat{y}^\mathbf{u } \leftarrow \mathsf {1fe}.\mathsf {Dec}(\mathsf {sk}_{\mathsf {E}^\mathbf{u }},\mathsf {ct}_\mathbf{u })\).
-
Compute \(\mathsf {Decode}\left( \left\{ \widehat{y}^\mathbf{u } \right\} _\mathbf{u \in \mathbf {S}}, \mathbf {S}\right) \) to obtain y.
-
Output y.
Correctness. Consider a circuit C and an input x. Suppose \(\mathsf {CT}\leftarrow \mathsf {Enc}(\mathsf {MPK},x)\) and \(\mathsf {SK}_{C} \leftarrow \mathsf {KeyGen}(\mathsf {MSK},C)\). Let \(\mathsf {CT}=(\mathsf {ct}_1,\ldots ,\mathsf {ct}_N)\) and \(\mathsf {SK}_C=\left( \mathbf {S},\ \left\{ \mathsf {sk}_{\mathsf {E}^\mathbf{u }} \right\} _\mathbf{u \in \mathbf {S}} \right) \). By the correctness of \(\mathsf {1fe}\), \(\mathsf {1fe}.\mathsf {Dec}(\mathsf {sk}_{\mathsf {E}^\mathbf{u }},\mathsf {ct}^\mathbf{u })=\mathsf {Local}(\widehat{C}^\mathbf{u },\widehat{x}^\mathbf{u })\) for every \(\mathbf u \in \mathbf {S}\). From the correctness of \(\varPi \), it follows that \(\mathsf {Decode}\left( \left\{ \mathsf {Local}(\widehat{C}^\mathbf{u },\widehat{x}^\mathbf{u })\right\} _\mathbf{u \in \mathbf {S}},\mathbf {S}\right) =C(x)\).
We present the proof of security in the full version [AV19].
Instantiation. The bounded-key functional encryption scheme described above makes black box usage of \(\mathsf {InpEnc}(\cdot )\) algorithm of \(\varPi \). Moreover, in the construction of \(\varPi \) (described in the full version [AV19]), pseudorandom generators are only used in \(\mathsf {InpEnc}(\cdot )\). Furthermore, \(\mathsf {InpEnc}(\cdot )\) only makes black box calls to the pseudorandom generator. Thus, assuming that \(\mathsf {1fe}\) makes black box usage of public-key encryption, the bounded-key functional encryption scheme described above, when instantiated with \(\varPi \), yields a bounded-key scheme that makes only oracle calls to cryptographic primitives (public-key encryption and pseudorandom generators). All that is left is to demonstrate the feasibility of a single-key adaptively-secure public-key functional encryption that makes black box usage of public-key encryption.
To show this, we first present an informal description of single-key public-key FE \(\mathsf {1fe}\) for \(\mathsf {P}/\mathsf {Poly}\) from [SS10].
-
\(\mathsf {1fe}.\mathsf {Setup}\left( 1^{\lambda },1^s \right) \): Sample 2s public keys \(pk_{i,b}\) (\(i \in [s], b\in \{0,1\}\)) and secret keys \(sk_{i,b}\) (\(i \in [s], b\in \{0,1\}\)) corresponding to a public-key encryption scheme. Call the master public key \(\mathsf {mpk}=\left( pk_{i,b} \right) _{i \in [s], b\in \{0,1\} }\) and the master secret key \(\mathsf {msk}=\left( sk_{i,b} \right) _{i \in [s], b\in \{0,1\}}\).
-
\(\mathsf {1fe}.\mathsf {KeyGen}(\mathsf {msk},C)\): Output \(\mathsf {sk}_C=\left( sk_{i,C_i} \right) \), where \(C_i\) denotes the \(i^{th}\) bit in the description of C. Output \(\mathsf {sk}_C\).
-
\(\mathsf {1fe}.\mathsf {Enc}(\mathsf {msk},x)\): Generate a garbling of \(U_{x}(\cdot )\), where \(U_{x}(\cdot )\) is a universal circuit that takes as input a circuit C of size s and outputs C(x). Call the resulting garbled circuit to be \(\mathsf {GC}\). Encrypt the \((i,b)^{th}\) wire label, for \(i \in [s],b \in \{0,1\}\), using \(pk_{i,b}\); call this ciphertext \(ct_{i,b}\). Output \(\mathsf {ct}=\left( \mathsf {GC},\left( ct_{i,b} \right) _{i \in [s], b\in \{0,1\}} \right) \).
-
\(\mathsf {1fe}.\mathsf {Dec}(\mathsf {sk}_C,\mathsf {ct})\): Decrypt \(ct_{i,C_i}\) using \(sk_{i,C_i}\) to obtain the \((i,C_i)^{th}\) wire label. Using all the wire labels recovered, evaluate the garbled circuit to obtain C(x).
The above construction only guarantees selective security; this construction was upgraded to adaptive security by [GVW12a]. This construction is described in Sect. 4.3 (page 14) of the ePrint version of [GVW12a] ([GVW12b], version posted on 06-Sep-2012 17:57:14 UTC). The ONEQFE scheme (that allows a single function query and adaptive simulation security) described in Sect. 4.3 is constructed from randomized encodings for P/poly (which can be based on one-way functions) along with BFFE scheme described in Sect. 4.2. Moreover, the BFFE scheme described in Sect. 4.2 can be based on any PKE scheme (see the first para of Sect. 4.2).
BFFE scheme makes black box usage of PKE. Also, the ONEQFE scheme makes black-box usage of the one-way function (used for randomized encoding) and the underlying procedures of the BFFE scheme.
Notes
- 1.
- 2.
We could define a notion where \(\mathsf {CktEnc}\) takes as input the randomness of the offline phase. It is however not clear how to build FE from such a notion.
- 3.
If n or more servers can be corrupted then the corrupted set can recover C(x) for any circuit C: this is because the corrupted servers can execute \(\mathsf {CktEnc}\) on input C, run the local computation procedure and then decode their outputs. Thus, such a notion would imply program obfuscation.
- 4.
By adaptive, we mean that the adversary can decide each circuit query as a function of all the previous circuit queries.
References
Applebaum, B., Brakerski, Z., Tsabary, R.: Perfect secure computation in two rounds. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 152–174. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_6
Ananth, P., Choudhuri, A.R., Goel, A., Jain, A.: Round-optimal secure multiparty computation with honest majority. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 395–424. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_14
Agrawal, S.: Stronger security for reusable garbled circuits, general definitions and attacks. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 3–35. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_1
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_15
Ananth, P., Jain, A., Sahai, A.: Achieving compactness generically: indistinguishability obfuscation from non-compact functional encryption. IACR Cryptology ePrint Archive 2015:730 (2015)
Agrawal, S., Rosen, A.: Functional encryption for bounded collusions, revisited. In: TCC, pp. 173–205 (2017)
Ananth, P., Vaikuntanathan, V.: Optimal bounded-collusion secure functional encryption. Cryptology ePrint Archive, Report 2019/314 (2019). https://eprint.iacr.org/2019/314
Benhamouda, F., Lin, H.: k-round multiparty computation from k-round oblivious transfer via garbled interactive circuits. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 500–532. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_17
Brakerski, Z., Lombardi, A., Segev, G., Vaikuntanathan, V.: Anonymous IBE, leakage resilience and circular security from new assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 535–564. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_20
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D.: From cryptomania to obfustopia through secret-key functional encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 391–418. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_15
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation. In: STOC (1988)
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_16
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: IEEE 56th Annual Symposium on Foundations of Computer Science, FOCS 2015, Berkeley, CA, USA, 17–20 October, 2015, pp. 171–190 (2015)
Cramer, R., et al.: Bounded CCA2-secure encryption. In: Kurosawa, K. (ed.) ASIACRYPT 2007. LNCS, vol. 4833, pp. 502–518. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76900-2_31
Chen, Y., Vaikuntanathan, V., Waters, B., Wee, H., Wichs, D.: Traitor-tracing from lwe made simple and attribute-based. Cryptology ePrint Archive, Report 2018/897 (2018). https://eprint.iacr.org/2018/897
Döttling, N., Garg, S.: From selective IBE to full IBE and selective HIBE. In: TCC, pp. 372–408 (2017)
Döttling, N., Garg, S.: Identity-based encryption from the Diffie-Hellman assumption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 537–569. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_18
Dodis, Y., Katz, J., Xu, S., Yung, M.: Key-insulated public key cryptosystems. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 65–82. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_5
Garg, S., Ishai, Y., Srinivasan, A.: Two-round MPC: information-theoretic and black-box. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 123–151. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_5
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: STOC (2013)
Goldwasser, S., Lewko, A.B., Wilson, D.A.: Bounded-collusion IBE from key homomorphism. In: TCC 2012
Garg, S., Srinivasan, A.: Single-key to multi-key functional encryption with polynomial loss. In: TCC, pp. 419–442 (2016)
Garg, S., Srinivasan, A.: Two-round multiparty secure computation from minimal assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 468–499. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_16
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_11
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. Cryptology ePrint Archive, Report 2012/521 (2012). https://eprint.iacr.org/2012/521
Heng, S.-H., Kurosawa, K.: k-resilient identity-based encryption in the standard model. In: Okamoto, T. (ed.) CT-RSA 2004. LNCS, vol. 2964, pp. 67–80. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24660-2_6
Itkis, G., Shen, E., Varia, M., Wilson, D., Yerukhimovich, A.: Bounded-collusion attribute-based encryption from minimal assumptions. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10175, pp. 67–87. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_3
Kitagawa, F., Nishimaki, R., Tanaka, K.: Obfustopia built on secret-key functional encryption. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 603–648. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_20
Li, B., Micciancio, D.: Compactness vs collusion resistance in functional encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 443–468. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_17
Sahai, A., Seyalioglu, H.: Worry-free encryption: functional encryption with public keys. In: Proceedings of the 17th ACM Conference on Computer and Communications Security, pp. 463–472. ACM (2010)
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: STOC (2014)
Yao, A.C.-C.: How to generate and exchange secrets (extended abstract). In: FOCS, pp. 162–167 (1986)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Ananth, P., Vaikuntanathan, V. (2019). Optimal Bounded-Collusion Secure Functional Encryption. In: Hofheinz, D., Rosen, A. (eds) Theory of Cryptography. TCC 2019. Lecture Notes in Computer Science(), vol 11891. Springer, Cham. https://doi.org/10.1007/978-3-030-36030-6_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-36030-6_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-36029-0
Online ISBN: 978-3-030-36030-6
eBook Packages: Computer ScienceComputer Science (R0)






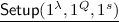 : On input security parameter
: On input security parameter  : On input master secret key
: On input master secret key  : On input master public key
: On input master public key  : On input functional key
: On input functional key 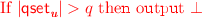 . Otherwise, send
. Otherwise, send 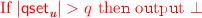 . Otherwise, send
. Otherwise, send 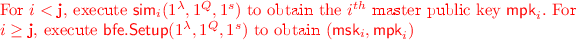 . Set
. Set  .
.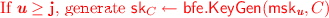 .
. .
.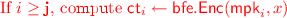 .
. .
.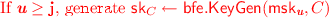 .
.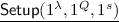 : On input security parameter
: On input security parameter 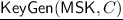 : On input master secret key
: On input master secret key  : On input master public key
: On input master public key 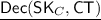 : On input functional key
: On input functional key 