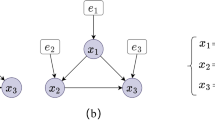
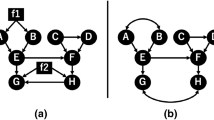
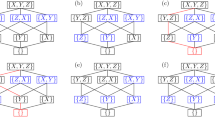
Abstract
Linear non-Gaussian Acyclic Model (LiNGAM) is a well-known model for causal discovery from observational data. Existing estimation methods are usually based on infinite sample theory and often fail to obtain an ideal result in the small samples. However, it is commonplace to encounter non-Gaussian data with small or medium sample sizes in practice. In this paper, we propose a Minimal Set-based LiNGAM algorithm (MiS-LiNGAM) to address the LiNGAM with small samples. MiS-LiNGAM is a two-phase and greedy search algorithm. Specifically, in the first phase, we find the skeleton of the network using the regression-based conditional independence test, which helps us reduce the complexity in finding the minimal LiNGAM set of the second phase. Further, this independence test we applied guarantees the reliability when the number of conditioning variables increases. In the second phase, we give an efficient method to iteratively select the minimal LiNGAM set with the skeleton and learn the causal network. We also present the corresponding theoretical derivation. The experimental results on simulated networks and real networks are presented to demonstrate the efficacy of our method.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Matlab package available at https://www.cs.helsinki.fi/u/ahyvarin/code/pwcausal/, Here, we adopt mxnt (maximum entropy approximations) to estimate the likelihood ratios in the Pairwise-LiNGAM algorithm.
- 2.
Matlab package available at https://sites.google.com/site/sshimizu06/Dlingamcode.
- 3.
Matlab package available at https://sites.google.com/site/sshimizu06/lingam.
References
Spirtes, P., Glymour, C., Scheines, R., Tillman, R.: Automated search for causal relations: theory and practice (2010)
Pearl, J.: The seven tools of causal inference, with reflections on machine learning. Commun. ACM 62(3), 54–60 (2019)
Lele, X., et al.: A pooling-lingam algorithm for effective connectivity analysis of fMRI data. Front. Comput. Neurosci. 8, 125 (2014)
Sanchez-Romero, R., Ramsey, J.D., Zhang, K., Glymour, M.R.K., Huang, B., Glymour, C.: Estimating feedforward and feedback effective connections from fMRI time series: assessments of statistical methods. Netw. Neurosci. 3(2), 274–306 (2019)
Zhang, K., Chan, L.: Minimal nonlinear distortion principle for nonlinear independent component analysis. J. Mach. Learn. Res. 9(Nov), 2455–2487 (2008)
Al-Yahyaee, K.H., Mensi, W., Al-Jarrah, I.M.W., Tiwari, A.K.: Testing for the Granger-causality between returns in the U.S and GIPSI stock markets. Phys. A: Stat. Mech. Appl. 531, 120950 (2019)
Cai, R., Zhang, Z., Hao, Z., Winslett, M.: Understanding social causalities behind human action sequences. IEEE Trans. Neural Netw. Learn. Syst. 28(8), 1801–1813 (2016)
Helajärvi, H., Rosenström, T., et al.: Exploring causality between TV viewing and weight change in young and middle-aged adults. The cardiovascular risk in young finns study. PLoS One 9(7), e101860 (2014)
Spirtes, P., Glymour, C.: An algorithm for fast recovery of sparse causal graphs. Soc. Sci. Comput. Rev. 9(1), 62–72 (1991)
Pearl, J., Verma, T.: A theory of inferred causation. In: Proceedings of the Second International Conference on Principles of Knowledge Representation and Reasoning, KR 1991, pp. 441–452 (1991)
Shimizu, S., Hoyer, P.O., Hyvärinen, A., Kerminen, A.: A linear non-Gaussian acyclic model for causal discovery. J. Mach. Learn. Res. 7(Oct), 2003–2030 (2006)
Shimizu, S.: LiNGAM: non-Gaussian methods for estimating causal structures. Behaviormetrika 41(1), 65–98 (2014)
Shimizu, S.: Non-gaussian methods for causal structure learning. Prev. Sci. 20, 1–11 (2018)
Hoyer, P.O., Hyttinen, A.: Bayesian discovery of linear acyclic causal models. In: Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, pp. 240–248. AUAI Press (2009)
Shimizu, S., et al.: DirectLiNGAM: a direct method for learning a linear non-Gaussian structural equation model. J. Mach. Learn. Res. 12(Apr), 1225–1248 (2011)
Hyvärinen, A., Smith, S.M.: Pairwise likelihood ratios for estimation of non-Gaussian structural equation models. J. Mach. Learn. Res. 14(Jan), 111–152 (2013)
Kagan, A.M., Rao, C.R., Linnik, Y.V.: Characterization problems in mathematical statistics (1973)
Zhang, H., Zhou, S., Zhang, K., Guan, J.: Causal discovery using regression-based conditional independence tests. In: Thirty-First AAAI Conference on Artificial Intelligence (2017)
Spirtes, P., Glymour, C.N., Scheines, R.: Causation, Prediction, and Search. MIT Press, Cambridge (2000)
Pearl, J.: Causality: Models, Reasoning and Inference, vol. 29. Springer, Heidelberg (2000)
Sogawa, Y., Shimizu, S., Shimamura, T., HyväRinen, A., Washio, T., Imoto, S.: Estimating exogenous variables in data with more variables than observations. Neural Netw. 24(8), 875–880 (2011)
Cai, R., Zhang, Z., Hao, Z.: SADA: a general framework to support robust causation discovery. In: International Conference on Machine Learning, pp. 208–216 (2013)
Hyvärinen, A., Zhang, K., Shimizu, S., Hoyer, P.O.: Estimation of a structural vector autoregression model using non-gaussianity. J. Mach. Learn. Res. 11(May), 1709–1731 (2010)
Hoyer, P.O., Shimizu, S., Kerminen, A.J., Palviainen, M.: Estimation of causal effects using linear non-gaussian causal models with hidden variables. Int. J. Approx. Reason. 49(2), 362–378 (2008)
Shimizu, S., Bollen, K.: Bayesian estimation of causal direction in acyclic structural equation models with individual-specific confounder variables and non-Gaussian distributions. J. Mach. Learn. Res. 15(1), 2629–2652 (2014)
Loh, P.-L., Bühlmann, P.: High-dimensional learning of linear causal networks via inverse covariance estimation. J. Mach. Learn. Res. 15(1), 3065–3105 (2014)
Cai, R., Xie, F., Chen, W., Hao, Z.: An efficient kurtosis-based causal discovery method for linear non-Gaussian acyclic data. In 2017 IEEE/ACM 25th International Symposium on Quality of Service, pp. 1–6. IEEE (2017)
Hoyer, P.O., et al.: Causal discovery of linear acyclic models with arbitrary distributions. In: Proceedings of the Twenty-Fourth Conference on Uncertainty in Artificial Intelligence, pp. 282–289. AUAI Press (2008)
Acknowledgement
This work was supported in part by the NSFC-Guangdong Joint Fund under Grant U1501254, in part by the Natural Science Foundation of China under Grant 61876043 and Grant 61472089, in part by the Natural Science Foundation of Guangdong under Grant 2014A030306004 and Grant 2014A030308008, in part by the Science and Technology Planning Project of Guangdong under Grant 2013B051000076, Grant 2015B010108006, and Grant 2015B010131015, in part by the Guangdong High-Level Personnel of Special Support Pro- gram under Grant 2015TQ01X140, in part by the Pearl River S&T Nova Program of Guangzhou under Grant 201610010101, and in part by the Science and Technology Planning Project of Guangzhou under Grant 201902010058.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Xie, F., Cai, R., Zeng, Y., Hao, Z. (2019). Causal Discovery of Linear Non-Gaussian Acyclic Model with Small Samples. In: Cui, Z., Pan, J., Zhang, S., Xiao, L., Yang, J. (eds) Intelligence Science and Big Data Engineering. Big Data and Machine Learning. IScIDE 2019. Lecture Notes in Computer Science(), vol 11936. Springer, Cham. https://doi.org/10.1007/978-3-030-36204-1_32
Download citation
DOI: https://doi.org/10.1007/978-3-030-36204-1_32
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-36203-4
Online ISBN: 978-3-030-36204-1
eBook Packages: Computer ScienceComputer Science (R0)