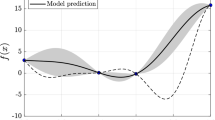
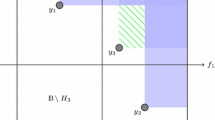
Abstract
Optimization of complex systems often involves running a detailed simulation model that requires large computational time per function evaluation. Many methods have been researched to use a few detailed, high-fidelity, function evaluations to construct a low-fidelity model, or surrogate, including Kriging, Gaussian processes, response surface approximation, and meta-modeling. We present a framework for global optimization of a high-fidelity model that takes advantage of low-fidelity models by iteratively evaluating the low-fidelity model and providing a mechanism to decide when and where to evaluate the high-fidelity model. This is achieved by sequentially refining the prediction of the computationally expensive high-fidelity model based on observed values in both high- and low-fidelity. The proposed multi-fidelity algorithm combines Probabilistic Branch and Bound, that uses a partitioning scheme to estimate subregions with near-optimal performance, with Gaussian processes, that provide predictive capability for the high-fidelity function. The output of the multi-fidelity algorithm is a set of subregions that approximates a target level set of best solutions in the feasible region. We present the algorithm for the first time and an analysis that characterizes the finite-time performance in terms of incorrect elimination of subregions of the solution space.
This work has been supported in part by the National Science Foundation, Grant CMMI-1632793.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
For an observed point \(x_i\), \(\hat{y}\left( x_i\right) =f(x_i)\) and \(s^{2}\left( x_i\right) =0\).
References
Conover, W.J.: Practical Nonparametric Statistics. Wiley, Hoboken (1980)
Frazier, P.: A tutorial on Bayesian optimization. arXiv:1807.02811v1 [stat.ML], 8 July 2018 (2018)
Gardner, J., Guo, C., Weinberger, K., Garnett, R., Grosse, R.: Discovering and exploiting additive structure for Bayesian optimization. In: Artificial Intelligence and Statistics, pp. 1311–1319 (2017)
Hoag, E., Doppa, J.R.: Bayesian optimization meets search based optimization: a hybrid approach for multi-fidelity optimization. In: Thirty-Second AAAI Conference on Artificial Intelligence (2018)
Huang, H., Zabinsky, Z.B.: Adaptive probabilistic branch and bound with confidence intervals for level set approximation. In: Proceedings of the 2013 Winter Simulation Conference: Simulation: Making Decisions in a Complex World, pp. 980–991. IEEE Press (2013)
Inanlouganji, A., Pedrielli, G., Fainekos, G., Pokutta, S.: Continuous simulation optimization with model mismatch using Gaussian process regression. In: 2018 Winter Simulation Conference (WSC), pp. 2131–2142. IEEE (2018)
Kandasamy, K., Dasarathy, G., Schneider, J., Póczos, B.: Multi-fidelity Bayesian optimisation with continuous approximations. In: Proceedings of the 34th International Conference on Machine Learning, vol. 70. pp. 1799–1808. JMLR.org (2017)
Kandasamy, K., Schneider, J., Póczos, B.: High dimensional Bayesian optimisation and bandits via additive models. In: International Conference on Machine Learning, pp. 295–304 (2015)
Li, C., Gupta, S., Rana, S., Nguyen, V., Venkatesh, S., Shilton, A.: High dimensional Bayesian optimization using dropout. arXiv:1802.05400 (2018)
Linz, D.D., Huang, H., Zabinsky, Z.B.: Multi-fidelity simulation optimization with level set approximation using probabilistic branch and bound. In: 2017 Winter Simulation Conference (WSC), pp. 2057–2068. IEEE (2017)
March, A., Willcox, K.: Provably convergent multifidelity optimization algorithm not requiring high-fidelity derivatives. AIAA J. 50(5), 1079–1089 (2012)
Mockus, J.: Bayesian Approach to Global Optimization. Kluwer Academic Publishers, Dordrecht (1989)
Mockus, J.: Application of Bayesian approach to numerical methods of global and stochastic optimization. J. Global Optim. 4, 347–365 (1994)
Poloczek, M., Wang, J., Frazier, P.: Multi-information source optimization. In: Advances in Neural Information Processing Systems, pp. 4288–4298 (2017)
Santner, T.J., Williams, B.J., Notz, W., Williams, B.J.: The Design and Analysis of Computer Experiments, vol. 1. Springer, New York (2003). https://doi.org/10.1007/978-1-4757-3799-8
Takeno, S., et al.: Multi-fidelity Bayesian optimization with max-value entropy search. arXiv preprint arXiv:1901.08275 (2019)
Törn, A., Zilinskas, A.: Global Optimization. Springer, Berlin (1989). https://doi.org/10.1007/3-540-50871-6
Wang, Z., Zoghi, M., Hutter, F., Matheson, D., De Freitas, N.: Bayesian optimization in high dimensions via random embeddings. In: Twenty-Third International Joint Conference on Artificial Intelligence (2013)
Wild, S.M., Regis, R.G., Shoemaker, C.A.: ORBIT: optimization by radial basis function interpolation in trust-regions. SIAM J. Sci. Comput. 30(6), 3197–3219 (2008)
Wu, J., Toscano-Palmerin, S., Frazier, P.I., Wilson, A.G.: Practical multi-fidelity Bayesian optimization for hyperparameter tuning. arXiv:1903.04703 (2019)
Xu, J., Zhang, S., Huang, E., Chen, C.H., Lee, L.H., Celik, N.: An ordinal transformation framework for multi-fidelity simulation optimization. In: 2014 IEEE International Conference on Automation Science and Engineering (CASE), pp. 385–390. IEEE (2014)
Xu, J., Zhang, S., Huang, E., Chen, C.H., Lee, L.H., Celik, N.: MO2TOS: multi-fidelity optimization with ordinal transformation and optimal sampling. Asia-Pac. J. Oper. Res. 33(03), 1650017 (2016)
Zabinsky, Z.B., Huang, H.: A partition-based optimization approach for level set approximation: probabilistic branch and bound. In: Smith, A.E. (ed.) Women in Industrial and Systems Engineering. WES, pp. 113–155. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-11866-2_6
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Zabinsky, Z.B., Pedrielli, G., Huang, H. (2019). A Framework for Multi-fidelity Modeling in Global Optimization Approaches. In: Nicosia, G., Pardalos, P., Umeton, R., Giuffrida, G., Sciacca, V. (eds) Machine Learning, Optimization, and Data Science. LOD 2019. Lecture Notes in Computer Science(), vol 11943. Springer, Cham. https://doi.org/10.1007/978-3-030-37599-7_28
Download citation
DOI: https://doi.org/10.1007/978-3-030-37599-7_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-37598-0
Online ISBN: 978-3-030-37599-7
eBook Packages: Computer ScienceComputer Science (R0)