Abstract
Next generation, i.e., fifth generation (5G), networks will leverage both fiber and wireless (FiWi) technology to meet the challenging 5G traffic demands. Moreover, a Cloud-Radio Access Network (C-RAN) architecture will be mainly adopted, which places the BaseBand Units (BBUs) at centralized locations, thus offering cost-efficient energy supply and climate control. To this end, efficient Medium Transparent-Medium Access Control (MT-MAC) protocols are needed to ensure the optimal exploitation of both media. In this paper, we propose a gated service MT-MAC protocol (gMT-MAC) for Millimeter Wave (mmWave) Analog Radio-over-Fiber (A-RoF) C-RANs. GMT-MAC grants a transmission window to each user equal to the time needed for its requested traffic to be successfully sent. A mean packet delay model is also proposed and verified by means of simulation. The performance of gMT-MAC is evaluated for different network load conditions, number of Remote Radio Heads (RRHs) and optical availability values. The provided results prove the suitability of gMT-MAC to meet the sub-ms delay requirements of latency-critical 5G services.
Supported by H2020-5G PPP 5G-PHOS (grant agreement 761989), MSCA ITN 5G STEP-FWD (grant agreement 722429), SPOT5G (TEC2017-87456-P) and AGAUR (2017 SGR 891).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Fifth Generation (5G) networks
- Mean packet delay model
- Fiber-Wireless (FiWi)
- Millimeter Wave (mmWave)
- Cloud-radio access networks (C-RANS)
- Analog Radio-over-Fiber (A-ROF)
- Medium Transparent-MAC (MT-MAC)
1 Introduction
Next generation, i.e., Fifth Generation (5G), networks increase peak data rate and cell edge data rate needs to 20 Gbps and 1 Gbps, respectively, compared to Forth Generation (4G) networks. In parallel, latency-critical 5G applications, also known as Ultra-Reliable Low Latency Communication (URLLC) applications, require lower than 1 ms end-to-end delay [1]. In order to meet these ever-increasing capacity and latency demands, the exploitation of higher spectrum bands, e.g., Millimeter Wave (mmWave), is expected to play a key role due to the huge bandwidth availability they offer. This trend is also reflected in Rel. 15 of 5G New Radio (NR) standard by 3GPP, which refers to the exploitation of spectrum bands up to 52.6 GHz, with Rel. 16 including even higher frequencies [2]. Nevertheless, mmWave bands experience high propagation losses, and therefore, enable shorter link ranges than traditional sub-6 GHz networks. As a result, when used in the Radio Access Network (RAN) part, they stress the need for antenna densification.
Hence, centralized architectures are favored, e.g., Cloud-RANs (C-RANs) [3], which separate BaseBand Units (BBUs) from Remote Radio Heads (RRHs), placing the former at centralized locations. Thereby, efficient network management as well as energy supply and climate control are achieved. Centralization, however, sets challenging capacity requirements for the BBU-RRH connection, also known as fronthaul, which should be able to support a massive number of broad mmWave channels. In parallel, the protocol specification used for the BBU-RRH communication, also known as Common Public Radio Interface (CPRI) [4], is highly inefficient in this case as it imposes up to two orders of magnitude bandwidth penalty compared to the IP rate. In this context, the need to design new efficient protocol solutions is imperative.
To that end, Analog-Radio-over-Fiber (A-RoF) technology has received increased attention from the research community mainly by virtue of its capability to meet both the centralization and high fronthaul capacity needs [5,6,7,8]. This is achieved by placing all main hardware, i.e., sampling and digital-to-analog conversion components, within the BBU, hence significantly simplifying the RRHs compared to Digital-Radio-over-Fiber (D-RoF) technology [9]. As a result, no bandwidth penalty is imposed on the fronthaul link, since no radio waveform digitization takes place and hence the full fiber bandwidth can be exploited to carry the mmWave channels [10]. On the other hand, by removing the inter-mediate digitization at the RRH, the optical and the wireless domains get completely separated one from the other. Thus, controlling both the optical and wireless resources from the centralized BBU pool, while meeting the strict 5G C-RAN delay requirements becomes a challenging problem to face.
A Medium Transparent-MAC (MT-MAC) scheme has been proposed to efficiently manage both the optical and wireless resources in Fiber-Wireless (FiWi) networks that employ A-RoF [11, 12]. In MT-MAC, the users have a direct communication with the BBU, while the RRHs perform solely the Radio Frequency (RF)/optical signal conversion. An enhanced MT-MAC version has been also proposed aiming at optimizing the size of the transmission window allocated to each RRH. In particular, contrary to the fixed allocation included in the traditional MT-MAC version, a more sophisticated allocation based on the number of active users, i.e., users that have traffic to be sent, located in the range of each RRH is performed. In other words, an RRH with a higher number of active users will be allocated a longer transmission window. Due to its client-weighted data wavelength allocation, this protocol version is also known as Client-Weighted MT-MAC [13, 14]. Client-Weighted MT-MAC was shown to achieve improved performance in terms of throughput and mean packet delay fairness compared to the fixed allocation of the traditional MT-MAC. Specifically, the fact that the size of the transmission window allocated to each user was the same regardless of the number of users that were sharing the same RRH resources, results in improved service equalization.
Although the aforementioned schemes achieve fairness either among RRHs (traditional MT-MAC, where the same transmission window size is allocated to each RRH), or among users (client-weighted MT-MAC, where the transmission window size allocated to each RRH is proportional to its number of active users), more sophisticated schemes are needed that will offer service equalization on a packet basis. To this end, the gated service scheme addresses this challenge by allocating transmission windows proportional to the number of packets located at the buffer of each user during the reporting phase. This scheme has received great research attention and has been also studied in the context of the Interleaved Polling with Adaptive Cycle Time (IPACT) protocol for Ethernet Passive Optical Networks (EPONs) [15, 16]. As shown in [17], gated service IPACT achieves considerable lower delay compared to fixed-service IPACT. Nonetheless, despite its unquestionable benefits, to the best of our knowledge, the gated service has never been exploited to MT-MAC protocol design for A-RoF FiWi C-RANs.
To that end, in this paper, we propose a gated service MT-MAC protocol (gMT-MAC), i.e., a protocol that grants a transmission window to each user equal to the amount of time needed to successfully send its reported traffic. An analytical model for the mean packet delay is also proposed and verified by means of simulation. The protocol performance is also evaluated for different network load conditions, number of RRHs and optical wavelength availability levels. Part of this work is based on the analysis of gated IPACT scheme for EPONs, presented in [17]. It has been appropriately adapted though for A-RoF FiWi C-RANs to account for the additional delay induced by the wavelength allocation and contention periods during the joint optical and wireless gMT-MAC time cycle. Thereby, the proposed work constitutes the first gated service model that addresses the joint wireless and optical resource allocation problem for FiWi C-RANs. On the contrary, the state-of-the-art either consists of RoF models addressing only the wireless resource allocation problem [18,19,20] or operates with fixed transmission window allocation [12]. The proposed model is shown to be in a very good agreement with the simulation results, thus proving the validity of both. Our results also prove the suitability of gMT-MAC for 5G C-RANs, since it is shown to be able to meet the sub-ms mean packet delay requirements of 5G latency-critical applications.
The rest of the paper is organized as follows. In Sects. 2 and 3, the system model and the gMT-MAC operation are described, respectively. In Sect. 4, the mean packet delay analytical model for is presented. Section 5 refers to the model validation by means of simulation. Specifically, the simulation scenario as well as the evaluation results are given, while useful insights are gained for the performance of gMT-MAC. Finally, Sect. 6 concludes the paper.
2 System Model
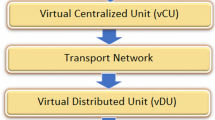
As shown in Fig. 1, the system model under study consists of a C-RAN network, in which a BBU is placed at a centralized location \(l_{f}\) meters away from R RRHs. A Passive Optical Network (PON) topology is also employed for the RRH interconnection. The parameter \(U_{r}\) refers to the number of users served by the RRH r. Poisson packet arrivals are assumed with bit rate equal to \(\lambda _U\) bps and a fixed packet length of \(l_{p}\). The buffer size of each user is B packets.
In order to tackle the increased complexity, a symmetric network in terms of number of users is assumed, i.e., \(U_1=U_2=...=U_r=U_R=U\). Hence, all RRHs have the same average packet arrival rate (bps), i.e., \(\lambda =U \lambda _U\). Nevertheless, it is worth pointing out that the number of packets located at the buffer of each user at a specific instant is a random parameter, although it follows the same distribution for all users and RRHs. Consequently, the same holds for the number of active users per RRH. These instantaneous changes are exploited by gated service schemes, which grant transmission windows proportional to the number of packets that each user requests at a specific time period.
We also assume W data wavelengths which can be transmitted through the same fiber link exploiting Wavelength Division Multiplexing (WDM). Another wavelength is also assumed, which is dedicated for control information exchange. The BBU-user communication over the FiWi link follows the gMT-MAC protocol, which will be detailed in Sect. 3. Finally, uplink and downlink operate at different frequencies, i.e., a node can receive and transmit concurrently.
3 Gated Service MT-MAC Protocol (gMT-MAC)
The proposed protocol comprises two parallel procedures, the allocation of data wavelength to the RRHs with active users and the allocation of resources to their users. For the data wavelength assignment, the BBU should initially be informed for the RRHs with users that have traffic to send. Therefore, it transmits a short pulse which is broadcasted to all users through their RRHs [12]. The users with pending traffic reply with the same pulse to their respective RRHs and from there the pulses are transmitted back to the BBU. For the identification of the RRHs that contain users with pending traffic, the difference in the distance between the BBU and each RRH is exploited, as it eventually leads to time difference between the reception of the pulses originated by different RRHs. Once the RRHs with pending traffic have been identified, a round robin allocation of the data wavelengths takes place among them. Specifically, a list is created including the RRHs with active users that have not been served yet. The RRH located first in the list has the highest priority in case a new data wavelength becomes available. On the other hand, in case a new RRH becomes active, it will be placed last.
Regarding the resource allocation to the active users of an RRH that has been assigned a data wavelength, it includes Request Resource Frames (RRFs) and data exchange frames. The first type of frames refers to the identification of the active users, while the second to the exchange of data information.
During an RRF, each active user picks up a random number between \([0, s_{RRF}-1]\), which represents the number of slots it has to wait until it transmits its ID packet to the BBU. The parameter \(s_{RRF}\) denotes the number of RRF slots. Hence, in each slot, the BBU transmits a POLL and the user with the respective chosen number replies with its ID, including its buffer (BF) status. Upon successful reception of the ID packet by the BBU, an ACK packet is transmitted to the user. In case more than one users choose the same number, a collision occurs and the BBU does not send an ACK. In this case, the collided users will participate to another RRF by choosing a new number from the set \([0, s_{RRF}-1]\). The RRF procedure will be repeated until either the maximum number of RRFs has been reached or all users have been successfully identified.
As for the data frame exchange process, each one of the identified users is being sequentially polled by the BBU to send its data. The polling sequence follows the user identification order. Due to the gated service employed by gMT-MAC, the transmission window allocated to each user is proportional to the number of reported packets located at its buffer during the identification process. Upon successful reception of the data packets of a polled user, the BBU sends an ACK packet following a procedure similar to the RRF process.
3.1 Operational Example of gMT-MAC
For a better understanding of gMT-MAC operation, an operational example referring (i) to the RRF process and (ii) to the data exchange process is given.
Request Resource Frame (RRF) Process. As shown in Fig. 2, we consider a simple example with 3 active users and \(s_{RRF}=4\) RRF slots. At the beginning of the RRF, each user selects a random number from the set [0, 3]. In the considered example, U1 selected number 3, U2 number 0 and U3 number 1. As a result, U1 will send its ID packet after waiting 3 slots, i.e., at slot 4, U2 without waiting at all, i.e., at slot 1 and U3 at slot 2. In each slot, the BBU transmits a POLL packet. Upon receiving the POLL, i.e., after \(T_{POLL}+\delta _{f}+\delta _{a}\), the user that selected the respective slot replies with its ID packet including its buffer status, BF. The parameters \(T_{POLL}\), \(\delta _{f}\) and \(\delta _{a}\) stand for the time duration of a POLL packet and the propagation delay in the fiber and in the wireless medium, respectively. The next POLL, which corresponds to slot 2, is scheduled \(T_{POLL}+ \delta _{f}+\delta _{a}\) before the end of slot 1. As a result, U3 that is scheduled to send its ID packet at slot 2, transmits it at the beginning of slot 2. The same procedure is repeated for the rest of the slots. Notice that slot 3 corresponds to an empty slot, since no user has selected it. Regarding the acknowledgment of the ID packet reception, ACK packets are sent together with the next POLL frames for higher bandwidth efficiency. In particular, an ACK is sent together with the next scheduled POLL frame as long as (i) the ID packet has been successfully received by the BBU, and (ii) there is another POLL packet to be sent. Hence, in the considered example, the ACK for the ID packet of U2 is sent together with the third POLL, while the ACK for the ID packet of U3 is sent together with the forth POLL. For the ID packet of U1, however, the ACK is sent immediately after the ID packet reception by the BBU, given that there is no other scheduled POLL frame left.
Thus, the RRF process duration can be given by
where \(T_{ID}\), \(T_{ACK}\) is the time duration of an ID and an ACK packet, respectively.
Example of data exchange process between the BBU and the 3 active users that have been identified based on the RRF process example of Fig. 2.
Data Frame Exchange Process. Regarding the data frame exchange process, a simple example is given in Fig. 3, assuming the same users that have been identified in the previous RRF example of Fig. 2. During the data frame exchange, a POLL packet is transmitted by the BBU for each active user sequentially in the order that they have been previously identified. Hence, initially U2 will be polled, then U3 and finally U1. For each user that is being polled, a transmission window is being granted based on the buffer status it reported during the identification process. Thus, a transmission window equal to the duration of 4 data packets is being granted to U2, of 2 data packets to U3 and of 6 data packets to U1. After each polled user has successfully sent its reported data to the BBU, an ACK is sent to the user. For higher bandwidth efficiency, similar to the RRF process, the ACK is sent together with the next POLL packet, as long as there is one. Hence, the ACK for the data packets of U2 is transmitted together with the third POLL. In the case there is no other POLL packet left, i.e., after all identified users have been polled, a single ACK is sent in the end of the process, which contains acknowledgement information for all the remaining data packets of the users. Moreover, given that there is no need to wait for the ACK packet to be received by the users, the duration of the data exchange process equals
with \(U_{act}\) denoting the number of active users that have been successfully identified in the previous RRF process.
4 Mean Packet Delay Analysis
We focus our analysis on the time period between two successive transmission windows of a specific RRH, denoted by \(T_{cyc}\). This parameter increases with the traffic load, since in gMT-MAC all users send as many data packets as they requested during the identification process. To calculate the average \(T_{cyc}\), we first derive its minimum value that equals a round-trip time in the fiber. Hence,
where \({\delta }_{f}=l_{f}/c_{f}\) is the propagation delay in the fiber, with \(l_{f}\) denoting the average fiber length and \(c_{f}\) being the speed of light in the fiber.
Thereafter, based on \(T_{cyc}^{min}\) calculation, we derive the minimum cycle time under traffic load as the sum of \(T_{cyc}^{min}\) and the amount of time needed to send the packets that have been generated by all RRHs in a minimum cycle time, i.e.,
where \(\varLambda =(R/W)\lambda \) denotes the total packet arrival rate (bps) of all RRHs. The parameters \(T_p\), \(T_{POLL}\), \(T_{ACK}\) refer to the duration of a data packet, a POLL and an ACK packet, respectively. In general, the duration of a packet x of \(l_x\) bits is given by \(T_{x}={l_x}/{D_u}\), with \(D_u\) being the uplink channel capacity (bps).
The properties of the Poisson traffic enable us to derive an approximate distribution of cycle times. Given that the number of packets is an integer number, the duration of a cycle m can take solely discrete values, i.e.,
with \(T_{RRF}\) being the RRF duration, given by (1).
By solving (5) in terms of m and setting \(T_{cyc}^{m}={T_{cyc}^{min}}'\), we derive the minimum value of m, denoted by \(m_{min}\). We then model the evolution of cycle times as a discrete Markov chain and calculate the matrix of transition probabilities from a cycle to another, denoted by \(\mathbf{P} \). The longest cycle corresponds to the case where all user buffers are full. In this case, the total number of packets is \(B_{max}^{all}=B\cdot U \cdot (R/W)\). Hence, the transition probability to cycle times that are longer than the minimum cycle time under traffic load can be calculated as
The transition probability to the minimum cycle time under traffic load equals
Thus, we derive the steady state probabilities by solving the following system.
where \(\pi \) is the eigenvector reflecting the steady state transition probabilities to cycle time i, with i ranging from 0 to \({B_{max}^{all}}\). The average cycle time then equals
Considering that a packet is more likely to arrive at a longer cycle time, we can conclude that the probability that a packet arrives at a specific cycle is proportional to its length. Hence, the steady state probabilities are rewritten as
It is also worth pointing out that a packet that arrives on a specific cycle will not be sent during the first transmission window, given that the user has first to notify the BBU for its buffer status and successfully receive the POLL packet before initiating the data transmission. Moreover, packet arrivals take place on average half-way between two transmission windows due to non-bursty nature of Poisson traffic. Hence, a packet stays in the queue on average for one-and-a-half cycles, and consequently the mean packet delay can be approximated by
5 Model Validation
5.1 Simulation Scenario
The proposed mean packet delay model was developed in MATLAB®, whereas for the simulations the Java discrete-event simulator, presented in [12], was modified accordingly so as to consider the gated service related features of gMT-MAC. In our results, we study different R/W ratio values due to the high impact of this parameter on the system performance. Per RRH, U = 5 users are considered, while the fiber length has a mean value of \(l_{f}\) = 1 km and variance 5 m. The rest of the simulation parameters are summarized in Table 1.
5.2 Results
In Fig. 4, the mean packet delay versus the normalized offered load is shown for different R/W ratio values for both the analytical model and the simulations. Please note that the system operates under stable conditions for normalized offered load up to 0.8. In other words, the network throughput is equal to the offered load and consequently there are no dropped packets. However, above this value, the network becomes unstable, i.e., with non-zero packet drops.
The analytical model is shown to be in a very good agreement with the simulation results for all R/W ratio values, which proves the validity of both. Nevertheless, for 0.9 normalized offered load, the network becomes unstable, making the queues susceptible to small variations caused by the probabilistic Poisson traffic, which accounts for the small model-simulations gap.
We can also observe that the mean packet delay increases with the offered load and R/W ratio value increase. It is worth pointing out, however, that in all cases, when the system operates under stable conditions, the mean packet delay remains below 1 ms. Thereby, the suitability of gMT-MAC is proved to satisfy the challenging 5G delay requirements e.g., of URLLC services.
6 Conclusions
In this paper, we proposed gMT-MAC, an MT-MAC protocol for mmWave A-RoF C-RANs, which employs gated service for maximum bandwidth efficiency. We also proposed a mean packet delay model, which was verified by means of simulation for different R/W ratio values and network load conditions. Our results showed: (i) that the proposed model closely matches the simulations, which proves the validity of both, and (ii) that gMT-MAC can be considered a promising 5G protocol able to address the challenging requirements of 5G C-RANs by offering sub-ms delay performance.
References
Chen, H., et al.: Ultra-reliable low latency cellular networks: use cases, challenges and approaches. IEEE Commun. Mag. 56(12), 119–125 (2018). https://doi.org/10.1109/MCOM.2018.1701178
Parkvall, S., Dahlman, E., Furuskar, A., Frenne, M.: NR: the new 5G radio access technology. IEEE Commun. Stand. Mag. 1(4), 24–30 (2017). https://doi.org/10.1109/MCOMSTD.2017.1700042
Agiwal, M., Roy, A., Saxena, N.: Next generation 5G wireless networks: a comprehensive survey. IEEE Commun. Surv. Tutor. 18(3), 1617–1655 (2016). https://doi.org/10.1109/COMST.2016.2532458. Thirdquater
CPRI Specification: Common Public Radio Interface (CPRI); Interface Specification. IEEE Communications Standards Magazine V7.0, October 2015
Liu, X., Zeng, H., Chand, N., Effenberger, F.: Efficient mobile fronthaul via DSP-based channel aggregation. J. Lightwave Technol. 34(6), 1556–1564 (2016). https://doi.org/10.1109/JLT.2015.2508451
Ishimura, S., Bekkali, A., Tanaka, K., Nishimura, K., Suzuki, M.: 1.032-Tb/s CPRI-equivalent rate IF-over-fiber transmission using a parallel IM/PM transmitter for high-capacity mobile fronthaul links. J. Lightwave Technol. 36(8), 1478–1484 (2018). https://doi.org/10.1109/JLT.2017.2787151
Giannoulis, G., et al.: Analog radio-over-fiber solutions for 5G communications in the beyond-CPRI era. In: 2018 20th International Conference on Transparent Optical Networks (ICTON), pp. 1–5, July 2018. https://doi.org/10.1109/ICTON.2018.8473886
Delmade, A., et al.: Performance analysis of analog IF over fiber fronthaul link with 4G and 5G coexistence. IEEE/OSA J. Opt. Commun. Netw. 10(3), 174–182 (2018). https://doi.org/10.1364/JOCN.10.000174
Novak, D., et al.: Radio-over-fiber technologies for emerging wireless systems. IEEE J. Quantum Electron. 52(1), 1–11 (2016). https://doi.org/10.1109/JQE.2015.2504107
Miyamoto, K., Kuwano, S., Terada, J., Otaka, A.: Split-PHY processing architecture to realize base station coordination and transmission bandwidth reduction in mobile fronthaul. In: 2015 Optical Fiber Communications Conference and Exhibition (OFC), pp. 1–3, March 2015. https://doi.org/10.1364/OFC.2015.M2J.4
Kalfas, G., Pleros, N.: An agile and medium-transparent MAC protocol for 60 GHz radio-over-fiber local access networks. J. Lightwave Technol. 28(16), 2315–2326 (2010). https://doi.org/10.1109/JLT.2010.2046394
Kalfas, G., Vardakas, J., Alonso, L., Verikoukis, C., Pleros, N.: Non-saturation delay analysis of medium transparent MAC protocol for 60 GHz fiber-wireless towards 5G mm wave networks. J. Lightwave Technol. 35(18), 3945–3955 (2017). https://doi.org/10.1109/JLT.2017.2723521
Kalfas, G., et al.: Client-weighted medium-transparent MAC protocol for user-centric fairness in 60 GHz radio-over-fiber WLANs. IEEE/OSA J. Opt. Commun. Netw. 6(1), 33–44 (2014). https://doi.org/10.1364/JOCN.6.000033
Mesodiakaki, A., et al.: Medium-transparent dynamic bandwidth allocation for 5G fiber wireless dense fronthaul networks. In: 2018 IEEE 23rd International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD), pp. 1–6, September 2018. https://doi.org/10.1109/CAMAD.2018.8514953
Ngo, M.T., Gravey, A., Bhadauria, D.: A mean value analysis approach for evaluating the performance of EPON with gated IPACT. In: 2008 International Conference on Optical Network Design and Modeling, pp. 1–6, March 2008. https://doi.org/10.1109/ONDM.2008.4578407
Miyata, S., Baba, K., Yamaoka, K.: Exact mean packet delay for delayed report messages multipoint control protocol in EPON. IEEE/OSA J. Opt. Commun. Netw. 10(3), 209–219 (2018). https://doi.org/10.1364/JOCN.10.000209
Lannoo, B., Verslegers, L., Colle, D., Pickavet, M., Gagnaire, M., Demeester, P.: Analytical model for the IPACT dynamic bandwidth allocation algorithm for EPONs. J. Opt. Netw. 6(6), 677–688 (2007). https://doi.org/10.1364/JON.6.000677. http://jon.osa.org/abstract.cfm?URI=jon-6-6-677
Fan, Y., et al.: Performance analysis for IEEE 802.11 distributed coordination function in radio-over-fiber-based distributed antenna systems. Opt. Express 21(18), 20529–20543 (2013). https://doi.org/10.1364/OE.21.020529. http://www.opticsexpress.org/abstract.cfm?URI=oe-21-18-20529
Pal, A., Nasipuri, A.: Performance analysis of IEEE 802.11 distributed coordination function in presence of hidden stations under non-saturated conditions with infinite buffer in radio-over-fiber wireless LANs. In: 2011 18th IEEE Workshop on Local Metropolitan Area Networks (LANMAN), pp. 1–6, October 2011. https://doi.org/10.1109/LANMAN.2011.6076921
Mjeku, M., Gomes, N.J.: Analysis of the request to send/clear to send exchange in WLAN over fiber networks. J. Lightwave Technol. 26(15), 2531–2539 (2008). https://doi.org/10.1109/JLT.2008.927202
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 IFIP International Federation for Information Processing
About this paper
Cite this paper
Mesodiakaki, A. et al. (2020). A Gated Service MAC Protocol for 5G Fiber-Wireless Cloud-Radio Access Networks. In: Tzanakaki, A., et al. Optical Network Design and Modeling. ONDM 2019. Lecture Notes in Computer Science(), vol 11616. Springer, Cham. https://doi.org/10.1007/978-3-030-38085-4_36
Download citation
DOI: https://doi.org/10.1007/978-3-030-38085-4_36
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-38084-7
Online ISBN: 978-3-030-38085-4
eBook Packages: Computer ScienceComputer Science (R0)