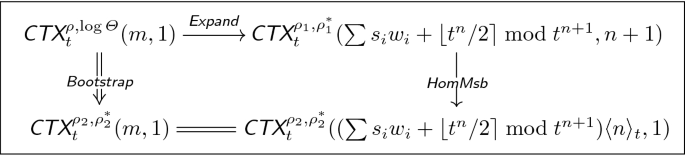Faster Bootstrapping of FHE over the Integers

Abstract

In FHE over the integers, decryption function is simplified by sparse subset subset sum problem (SSSP) assumption, which is introduced by Dijk et al. (Eurocrypt 2010), so that bootstrapping can be achieved successfully. Later, Nuida and Kurowasa (Eurocrypt 2015) proposed an advanced method of which the degree is very low and the message space is non-binary. These previous methods require low degree but more than $O(\lambda ^4)$ homomorphic multiplications which make them very slow. For a general bootstrapping method in FHE over the integers, the number of homomorphic multiplications and the degree of decryption function are important factors for the efficiency of bootstrapping procedure.

In this paper, we propose a new bootstrapping method for FHE over the integers requiring only $O(\log ^2 \lambda )$ homomorphic multiplications which is significantly lower than previous methods. Implementing our bootstrapping method on the scale-invariant FHE over the integers called CLT scheme, it takes 6 s for 500-bit message space and 80-bit security on a desktop. We also apply our bootstrapping method to the homomorphic evaluation of AES-128 circuit: It takes about 8 s per 128-bit block and is faster than the previous results of homomorphic AES evaluation using FHEs over the integers without bootstrapping.

K. Han—This work is done when the second author is in Seoul National University (SNU).

A Proof of Theorem and Lemmas

Lemma 3 (Noise growth analysis)

Let $c_1$, $c_2$ are ciphertext with noise $(\rho _1, \rho _1^*)$ and $(\rho _2, \rho _2^*)$, then

• $\texttt {SIDGHV.Add}_t^a(\textsf {pk}, c_1, c_2)$ is ciphertext with noise $(\rho + 2, \rho ^* + 1)$

• $\texttt {SIDGHV.Mult}_t^a(\textsf {pk}, c_1, c_2)$ is ciphertext with noise $(\rho + \rho ^* +a\log t + 8, \log \varTheta )$

Here $\rho = \textsf {max}(\rho _1 , \rho _2)$ and $\rho ^* = \textsf {max}(\rho _1^* , \rho _2^*)$.

Proof

First, lets prove about SIDGHV.Add part. Let $c_1, c_2$ as below.

$$c_1 = q_1 \cdot p^2 + \left\lfloor {p/t^a} \right\rfloor \cdot (m_1 + t^a r_1^*) + r_1,$$

$$c_2 = q_2 \cdot p^2 + \left\lfloor {p/t^a} \right\rfloor \cdot (m_2 + t^a r_2^*) + r_2.$$

Then addition of $c_1$ and $c_2$ is

$$\begin{aligned} c_1 + c_2= & {} (q_1 + q_2) \cdot p^2 + \left\lfloor {p/t^a} \right\rfloor \cdot ([m_1 + m_2]_{t^a} + t^a (r_1^* + r_2^* + 1/0)) + r_1 + r_2\\= & {} q_3 \cdot p^2 + \left\lfloor {p/t^a} \right\rfloor \cdot {(m_3 + t^a r_3^*)} + r_3 \end{aligned}$$

for $r_3^* < 2^{\rho _1^*} + 2^{\rho _2^*} + 1$ and $r_3 < 2^{\rho _1} + 2^{\rho _2}$. The ciphertext of $[m_1+m_2]_{2^a}$ is $c_3 = [c_1 + c_2]_{x_0} = c_1 + c_2 - k \cdot x_0$ for $k \in \{ 0,1 \}$ since $c_1 ,~c_2 < x_0$. Therefore, $c_3 \leftarrow \texttt {SIDGHV.Add}^a(\textsf {pk}, c_1, c_2)$ is a ciphertext $c_3 = q \cdot p^2 + \left\lfloor {p/t^a} \right\rfloor (m + t^a r^*) + r$ satisfying $r^* < 2^{\rho _1^*} + 2^{\rho _2^*} + 1$ and $r < 2^{\rho _1} + 2^{\rho _2} + 2^{\rho _0}$.

Second part is about SIDGHV.Mult algorithm. Let $c_1, c_2$ as defined above, and k,l be integers such that $\left\lfloor {p/t^a} \right\rfloor = (p-k) / t^a$ and $\left\lfloor {p^2/t^a} \right\rfloor = (p^2-l) / t^a$. Then following equation holds,

$$\begin{aligned} c_3 = t^a \cdot c_1 \cdot c_2= & {} q_3 \cdot p^2 + ((p-k)^2 / t^a) \cdot (m_1 + t^a r_1^*)(m_2 + t^a r_2^*) + R\\= & {} q_3 \cdot p^2 + ((p^2 - l) / t^a) \cdot (m_1 m_2 \bmod t^a) + R + R' \\= & {} q_3 \cdot p^2 + \left\lfloor {p^2 / t^a} \right\rfloor \cdot (m_1 m_2 \bmod t^a) + r_3 \end{aligned}$$

where $|R| < 3 \cdot 2^\eta \cdot t^a \cdot 2^{\rho ^*+\rho }$ and $|R'|< 2 \cdot 2^\eta \cdot t^{2a}\cdot 2^{2\rho ^*} +t^{2a}\cdot 2^{2\rho ^*}<3 \cdot 2^\eta \cdot t^{2a}\cdot 2^{2\rho ^*}$. Therefore, the inequality $|r_3| < 6 \cdot 2^{\eta + a\log t + \rho + \rho ^*}$ holds when assuming $a\log t+\rho ^*<\rho$.

Now we will analyze the error of ciphertext after processing $\texttt {Convert}$ procedure. We followed the proof of lemma 1 in [6]. Let $\lceil \log r_3 \rceil = \rho _3 < \eta + 2a\log t + \rho + \rho ^* + 3$ and $c \leftarrow \texttt {Convert}(c_3/t)$, then from the following equation:

$$\varvec{\sigma }=p^2 \cdot \varvec{q} + \varvec{r} + \lfloor \varvec{s'} \cdot \dfrac{p}{2^{\eta +1}} \rceil .$$

Let $\varvec{c}'= \textsf {BitDecomp}_\eta (\varvec{c})$, then we have:

$$c = 2 \langle \varvec{\sigma }, \varvec{c'} \rangle = 2p^2 \cdot \langle \varvec{q},\varvec{c'} \rangle + 2 \langle \varvec{r} , \varvec{c'} \rangle + 2 \langle \lfloor \varvec{s'} \cdot \dfrac{p}{2^{\eta +1}} \rceil , \varvec{c'} \rangle .$$

Since the components of $\varvec{c'}$ are bits,

$$2 \langle \lfloor \varvec{s'} \cdot \dfrac{p}{2^{\eta +1}} \rceil , \varvec{c'} \rangle = \langle \dfrac{p}{2^\eta }\cdot \varvec{s'},\varvec{c'}\rangle + \nu _2 = \dfrac{p}{2^\eta } \langle \varvec{s'},\varvec{c'}\rangle + \nu _2,$$

where $|\nu _2|<\varTheta \cdot \eta$. From the definition of BitDecomp and PowersofTwo, we have $\langle \varvec{s'},\varvec{c'} \rangle = \langle \varvec{s},\varvec{c} \rangle \bmod 2^\eta = \langle \varvec{s}, \varvec{c}\rangle + q_2 \cdot 2^\eta$. Moreover

$$\langle \varvec{s} , \varvec{c} \rangle = \sum s_i \left\lfloor \frac{c_3}{t} \cdot z_i \right\rceil + \varDelta \cdot 2^\eta = \sum \frac{s_i \cdot c_3 \cdot z_i}{t} + \delta _1 + \varDelta \cdot 2^\eta = \frac{c_3}{t} \cdot \langle \varvec{s}, \varvec{z}\rangle + \delta _1 + \varDelta \cdot 2^\eta ,$$

for some $\varDelta \in \mathbb {Z}$ and $| \delta _1 | \le \varTheta /2$. Using $\langle \varvec{s} , \varvec{z} \rangle = 2^\eta \cdot t / p^2 - \epsilon - \mu \cdot 2^\eta \cdot t$ for some $\mu \in \mathbb {Z}$, and $c_3 = r_3 + \left\lfloor {p^2/t^a} \right\rfloor \cdot m + q _3\cdot p^2$, this gives following equation:

$$ \langle \varvec{s}, \varvec{c}\rangle = q_3 \cdot 2^\eta + \dfrac{2^{\eta }}{t^a}\cdot m - \dfrac{2^{\eta }\cdot \ell }{p^2t^a} \cdot m + r_3 \cdot \dfrac{2^\eta }{p^2} - \frac{c_3}{t} \cdot \epsilon + \delta _1 + (\varDelta - c_3 \cdot \mu )\cdot 2^\eta . $$

Therefore we can write

$$ \langle \varvec{s}, \varvec{c} \rangle = q_1 \cdot 2^\eta + m \cdot \dfrac{2^{\eta }}{t^a} + r^* $$

for some $r^* \in \mathbb {Z}$, with $| r^* | \le 2^{\rho _3 - \eta + 3}$. Now we get an equation below:

$$2 \left\langle \left\lfloor \dfrac{p}{2^{\eta +1}} \cdot \varvec{s'} \right\rceil , \varvec{c'}\right\rangle = q_4 \cdot p + m \cdot \dfrac{p}{t^a} + r^* \cdot \dfrac{p}{2^\eta } + \nu _2$$

with $| q_4 | \le \varTheta$; namely the components of $(p/2^{\eta +1}) \cdot \varvec{s'}$ are smaller than p and $\varvec{c'}$ is a binary vector. This gives

$$ 2 \left\langle \left\lfloor \dfrac{p}{2^{\eta +1}} \cdot \varvec{s'} \right\rceil , \varvec{c'}\right\rangle = (t^a q_4 + m) \cdot \left\lfloor \dfrac{p}{t^a} \right\rfloor + r_2^*$$

with $| r_2^* | \le 2^{\rho _3 - \eta + 4}$. Then we obtain:

$$\begin{aligned} c= & {} 2p^2 \cdot \langle \varvec{q}, \varvec{c'} \rangle + 2 \langle \varvec{r}, \varvec{c'} \rangle + (t^a q_4 + m) \cdot \left\lfloor { \dfrac{p}{t^a} } \right\rfloor + r_2^*\\ c= & {} 2q'' \cdot p^2 + (t^a q_4 + m) \cdot \left\lfloor { \dfrac{p}{t^a} } \right\rfloor + r' \end{aligned}$$

where $|r'| \le |r_2^*| + \eta \cdot \varTheta \cdot 2^{\rho +1} \le 2^{\rho _3 - \eta + 4} + \eta \cdot \varTheta \cdot 2^{\rho + 1} < 2^{a \log t+ \rho + \rho ^* + 7} + \eta \cdot \varTheta \cdot 2^{\lambda +1}$. Therefore, the return ciphertext c has following noise:

$$ (\rho + \rho ^* + a\log t + 8 , \log \varTheta ) \text { if } a \log t + \rho + \rho ^* + 5 > \log \eta + \log \varTheta + \lambda . $$

Above equation prove the second part of this lemman.    $\square$

Lemma 4

(Correctness of ). For given $m = b_{0,0}$, define $b_{i,j}$:

$$\begin{aligned}&b_{i,0} = ( {b_{0,0} - \sum _{j = 0}^{i-1} t^{j} \cdot b_{j,i-j} \bmod t^{n+1}} ) / {t^i} \text { for } 1 \le i \le n \\&\text {and }b_{i,j+1} = F_{t,n}(b_{i,j}) \text { for } 0 \le i < n,~ 0 \le j \le n-i. \end{aligned}$$

If $c_0 = \mathcal {E}_{n+1}(b_{0,0})$, and

$$c_{i,0} = c_{0,0} - \sum _{j = 0}^{i-1} c_{j,i-j} \text { for } 1 \le i \le n$$

$$ \&\ c_{i,j+1} = \texttt {SIDGHV.Eval}_t^{n-i+1}(\textsf {pk}, F_{t,n}, c_{i,j}) \text { for } 0 \le i < n ,~0 \le j \le n-i .$$

Then, $c_{i,0} = \mathcal {E}_{n-i+1}(b_{i,0})$ for $0 \le i \le n$.

Proof

We use induction on i. The statement is clear when $i=0$. Suppose the proposition is true for $i < m$. Then we have

$$\begin{aligned} c_{m,0}= & {} c_{0,0} - \sum _{j = 0}^{m-1} c_{j,m-j} \\= & {} c_0 - \sum _{j=0}^{m-1} \mathcal {E}_{n-j+1}\left( F_{t,n}^{m-j}(b_{j,0}) \right) \\= & {} c_0 - \sum _{j=0}^{m-1} \mathcal {E}_{n+1}\left( t^j F_{t,n}^{m-j}(b_{j,0}) \right) \\= & {} \mathcal {E}_{n+1}\left( b_{0,0} - \sum _{j = 0}^{m-1}t^j F_{t,n}^{m-j}(b_{j,0})\right) \\= & {} \mathcal {E}_{n+1}\left( b_{0,0} - \sum _{j = 0}^{m-1} t^{j}b_{j,m-j} \bmod t^{n+1}\right) .\\= & {} \mathcal {E}_{n+1}\left( t^m b_{m,0}\right) = \mathcal {E}_{n+1-m}(b_{m,0}). \end{aligned}$$

Then we can see that this lemma holds for any positive $i \le n$. And this means $c_{n,0} = \mathcal {E}_{1}(b_{n,0}) = \mathcal {E}_{1}(m\langle n \rangle _t)$, so this lemma shows the correctness of our bootstrapping procedure.    $\square$

Theorem 1

(Correctness and Noise analysis of Bootstrap). $c^* \leftarrow \textsf {Bootstrap}(\textsf {pk}, c)$, then $c^*$ is ciphertext with noise 810

$$\begin{aligned} (\rho _2,\rho _2^*) = \left( \rho + (n+1)\log t +\log (\varTheta '+1)+ n\log t (\log t +\log \varTheta + 8)\cdot (1+\epsilon ),~\log \varTheta + n\right) \end{aligned}$$

for $\epsilon = \left( \frac{n+1}{2}\cdot \log t +t + \frac{n+2}{\log t}\right) /(\log t + \log \varTheta +8)$ and two ciphertext c, $c^*$ with same messages.

Proof

• 1. Expand

  $v_i = q_i \cdot p^2 + \left\lfloor { \dfrac{p}{t^{n+1}} } \right\rfloor \cdot s_i + r_i$ and $v_0 = q \cdot p^2 + \left\lfloor { \dfrac{p}{t^{n+1}} } \right\rfloor \cdot \left\lfloor {\dfrac{t^{n}}{2}} \right\rfloor + r$ with $q, ~q_i \in [0, q_0)$ and $r,~ r_i \in (-2^{\rho }, 2^{\rho })$ for $1 \le i \le \varTheta '$. So if $c_{0,0} \leftarrow \textsf {Expand}(c,\varvec{y})$, then

  $$c_{0,0} = q' \cdot p^2 + \left\lfloor { \dfrac{p}{t^{n+1}}} \right\rfloor \cdot \left( \left( \sum s_i w_i + \left\lfloor {\dfrac{t^{n}}{2}} \right\rfloor \right) \bmod t^{n+1} + r^* t^{n+1}\right) + r'$$

  for $|r'| = |\sum _{i=1}^{\varTheta '}w_i r_i + r| < (\varTheta ' + 1)2^{\rho + (n +1)\log t}$ and $|r^*| \le \varTheta '$. Therefore, $c_{0,0}$ is a ciphertext with noise $(\rho _1 , \rho _1^*) = (\rho + (n + 1) \log t + \log (\varTheta '+1),~ \log \varTheta ')$ whose message space is $\mathbb {Z}_{t^{n+1}}$.

• 2. HomMsb

  Let $c_{i,j}$ is a ciphertext with noise $(\rho _{i,j}, \rho _{i,j}^*)$, then the equations $\rho _{0,0} = \rho + (n + 1) \log t + \log (\varTheta ' + 1)$ and $\rho _{0,0}^*=\log \varTheta '$ holds by above $\textsf {Expand}$ procedure. By applying Lemma 3, we can set

  $$\rho _{i,0}= \textsf {max}\{\rho _{0,i},\cdots ,\rho _{i-1,1}\} + 2i,~\rho _{i,0}^*= \log \varTheta + i\log t$$

  for $1 \le i \le n$.

  First, we will show the equality

  $$\textsf {max}\{\rho _{0,i+1},\cdots ,\rho _{i,1}\} = \rho _{i,1}$$

  holds for $0 \le i \le n-1$. Since $c_{j,i-j+1} = \textsf {SIDGHV.Eval}_t^{n-j+1}(\textsf {pk}, F_{t,n}, c_{j,i-j})$ for $0 \le j \le i$, it is sufficient to compare noise increase of $c_{j,i-j}$ after $\textsf {SIDGHV.Mult}_t^a$. For $1 \le j \le i-1$, the increase of first noise of $c_{j,i-j}$ is less than or equal to $\log \varTheta +(n+1)\log t +8$, and the increase of noise of $c_{i,0}$ is $\rho _{i,0}^*+ (n-i+1)\log t +8=\log \varTheta +(n+1)\log t +8$. Therefore, the equality $\textsf {max}\{\rho _{0,i+1},\cdots ,\rho _{i,1}\} = \rho _{i,1}$ holds and we can get

  $$\rho _{i,0}= \rho _{i-1,1} + 2i.$$

  Second, we will analyze the noise increase in while evaluating $F_{t,n}$. $F_{t,n}$ is a polynomial of degree t and its coefficients are bounded by $t^{n+1}$. Then, we can regard each term of $F_{t,n}$ is contained by at most t times of multiplications, so we get $\rho _{i-1,1}=\rho _{i-1,0}+ \lceil \log t \rceil \cdot (\log t \cdot (n-i+2) + \log \varTheta +8) + t \lceil \log t \rceil .$ Now, we obtain a recursion formula :

  $$\rho _{i,0}=\rho _{i-1,0}+\lceil \log t \rceil \cdot (\log t \cdot (n-i+2) + \log \varTheta +8) + t \lceil \log t \rceil +2i.$$

  The consequence of the recursion formula is

  $$\begin{aligned} \rho _{n,0}= & {} \rho _{0,0} + \log ^2 t \cdot \dfrac{n^2+3n}{2}+n\log t (\log \varTheta + 8)+ nt\log t + n^2+2n\\= & {} \rho _{0,0} + n\log t (\log t + \log \varTheta +8) (1+ \epsilon ) \end{aligned}$$

  for $\epsilon = \left( \frac{n+1}{2}\cdot \log t +t + \frac{n+2}{\log t}\right) /(\log t + \log \varTheta +8).$

• 3. Correctness

  

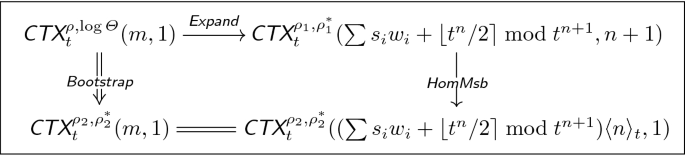
  Top side of the diagram was proved in 1. $\textsf {Expand}$. Also, Lemma 4 and 2. $\textsf {HomMsb}$ exactly signify the right side of the diagram, and the discussion in Sect. 4.3 shows the equality $m = (\sum s_i w_i +\lfloor t^{n}/2 \rceil \bmod t^{n+1})\langle n \rangle _t$ holds so that bottom side of the diagram is proved.    $\square$