Keywords

1 Introduction

Within the European Horizon 2020 project ACDC – Artificial Cells with Distributed Cores to Decipher Protein Function, our group aims at the development of a cheap and small portable biochemical laboratory being able to e.g. produce any desired macromolecule, like antibiotics, on demand. For this purpose, biologically inspired structures, namely droplets comprised of some fluid and being surrounded by another fluid, shall be used. The droplets may also contain chemicals and can be enclosed within some outer hulls, mimicking the role membranes have for cells. Neighboring droplets can form bilayers and can exchange the chemicals within them through pores in these bilayers, thus allowing for chemical reactions. A specific three-dimensional arrangement of droplets and a resulting bilayer network is then intended to produce a desired chain of reactions, e.g. resulting in a macromolecule via a gradual biochemical reaction scheme. In order to govern the process of creating a specific three-dimensional arrangement of droplets within the biochemical laboratory, a control unit is needed which is termed ’chemical compiler’ by us. This chemical compiler must be able to define with which chemicals the various droplets need to be filled and to determine which bilayer networks could be used for the desired biochemical reaction chain. It also needs to foretell how to create a three-dimensional arrangement of droplets from the originally one-dimensional lineup of droplets [1], leading to one of the required bilayer networks. For the development of such a compiler, still a lot of research has to be invested. We already proved that the existence of such a compiler is possible, both by showing for an example that it can be created [2] and by providing a general mapping from a computer program written only with the commands if-​then-​else and goto onto a biochemical reaction scheme [3]. But we also already showed that not any bilayer network desired for a specific biochemical reaction chain can be created, due to physical and mathematical limitations to achievable three-dimensional arrangements of droplets [4].

In order to finally be able to build such a device and to control it by means of such a compiler, we have to get a better understanding of the consequences of experimental settings and other input parameters of experiments, of the experimental progress, and also of the outcome of the experiments. The process of creating droplets is in the meantime very well understood and can be governed at will [1, 5,6,7,8,9,10,11], especially by the usage of 3D printing technology, which has become a widely used technique in the field of microfluidics [12,13,14,15,16,17,18,19]. We thus consider the general problem of producing droplets to be solved, except that the compiler has to choose appropriate antechambers for the production process or even to create them using the 3D printing technology.

Fig. 1.
figure 1

Sketch of the initial and final states of the spatial rearrangement of droplets.

Full size image

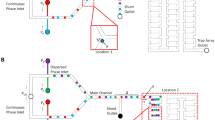
However, the process of creating three-dimensional arrangements of droplets from original one-dimensional lineups, as shown in Fig. 1, is not yet fully understood and is still a current research project. Our collaborating experimental group at Cardiff University currently extends the boundaries of this field, now being able to include more than 100 droplets swirling within a droplet of a diameter of roughly 1 cm [20]. Thus, in one part of our project, we want to understand how this transition works and to perform Monte Carlo simulations mimicking the experimental setup, as described in [4]. We will of course never be able to accurately reproduce the overall experiment in our simulations, due to lack both of computing time and of information about experimental parameters. However, we intend to adjust the parameters for the simulation in a way that the resulting configurations reflect the three-dimensional arrangements of droplets as found in experiments. But of equal importance is the question of the outcoming three-dimensional configurations, which are not always the same, as seen in movies generated from experiments [20]. Instead of a one-and-only final configuration, various arrangements are achieved. But when looking closely at the resulting configurations, one finds that they are not entirely random and are often rather similar to each other and that maybe even some configurations might be identical.

As already mentioned, we will finally have to rely on the existence of bilayer networks allowing for the complex gradual reaction scheme in order to produce the desired reaction structures. Therefore, we have the task to closely investigate the resulting three-dimensional configurations both from experiments and from simulations, which proves to be a very difficult problem, as described in the next sections. In Sect. 2, we start off with describing when we consider two differently looking configurations to be identical. In Sect. 3, we continue this consideration by describing how to detect that two configurations are indeed identical. But as already mentioned, the resulting configurations from experiments are not always identical, such that we continue with various approaches dealing with differences among them. If there are only small differences among various configurations, which are caused by single droplets that might be differently connected and placed, then searching for a network core might be the suitable strategy as mentioned in Sect. 4. But if the resulting configurations are more than only slightly different, a strategy called Searching for Backbones detecting network parts common to all configurations, which are called backbones, has to be applied as described in Sect. 5. However, there could be so many differences among the resulting configurations that not even a single larger backbone can be found. But still, there could be various groups of configurations with only little differences among the configurations within each group and larger differences between configurations in different groups. Sections 6 and 7 provide two approaches for detecting such groups and ways how to merge them into even larger supergroups.

Fig. 2.
figure 2

Top: Two resulting three-dimensional arrangements of droplets filled with various chemicals. Bottom: Corresponding bilayer networks between the droplets. We made these bilayer networks visible by reducing the size of the droplets and printing a connecting edge between a pair of neighboring droplets if they have formed a bilayer.

Full size image

2 Comparing Resulting Configurations

Two exemplary three-dimensional arrangements of droplets are shown in the upper half of Fig. 2. At first sight, they look different, but this might be the case for any two three-dimensional spherical objects consisting of various constituents. Usually, one would claim that two such three-dimensional objects are identical if they can be made congruent by rotation and mirroring. However, in our problem, the various droplets can be more or less deformed, such that the congruency method has to fail. And we do not need to care about what the overall configuration exactly looks like, all we need to care about is the underlying bilayer network formed by the bilayers between pairs of droplets, allowing for or denying the complex gradual reaction scheme we have in mind.

Concluding, for our problem, two three-dimensional arrangements are identical if their underlying bilayer networks are identical, because due to their identity, they lead to identical possibilities for chemical reactions and thus to identical reaction results.

Fig. 3.
figure 3

Simple example for the graph isomorphism problem: The two graphs shown are not identical at first sight. But using the isomorphism \(E=3, A=5, B=4, D=1,\) and \(C=2\), one finds that these two graphs can be transferred one into the other by this isomorphism and can thus be considered to be identical.

Full size image

3 The Graph Isomorphism Problem

Thus, the question arises how to show that two such bilayer networks are identical. At first, one might think that it must be easy to see that two such networks are identical, but this is not the case, as we want to demonstrate at a simple example shown in Fig. 3. This example consists of two graphs (Throughout this paper, we will use both the term network, which is used in physics and biology, and the term graph, which is used by mathematicians. Both terms describe the same.) with five nodes and seven edges each. At first sight, these two graphs seem to be different. This seemingly difference could be caused by e.g. rotating and mirroring the droplet configuration, such that we could be misled by eyesight. In order to avoid this effect, usually, the adjacency matrix \(\eta _G\) of graph G is considered with

$$\begin{aligned} \eta _G(i,j)= {\left\{ \begin{array}{ll} 1 &{} \mathrm{if\,\, nodes}\,\, i \,\,\textrm{and} \,\,j\,\, \mathrm{are \,\,connected}\,\, \\ &{} \mathrm{by\,\, an\,\, edge\,\, in\,\, graph\,\, }\,\,G\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,. \\ 0 &{} \textrm{otherwise} \\ \end{array}\right. } \end{aligned}$$
(1)

For the left graph (lg) and the right graph (rg) in Fig. 3, we thus get the corresponding adjacency matrices

$$\begin{aligned} \eta _{\textrm{lg}}=\left( \begin{array}{ccccc} 0 &{} 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 0 &{} 1 &{} 0 &{} 0 \\ 1 &{} 1 &{} 0 &{} 1 &{} 1 \\ 0 &{} 0 &{} 1 &{} 0 &{} 1 \\ 1 &{} 0 &{} 1 &{} 1 &{} 0 \\ \end{array}\right) \text{ and } \eta _{\textrm{rg}}=\left( \begin{array}{ccccc} 0 &{} 1 &{} 0 &{} 1 &{} 1 \\ 1 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 &{} 1 \\ 1 &{} 0 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 &{} 0 \\ \end{array}\right) , \end{aligned}$$
(2)

rsp., with the node orderings \(1-2-3-4-5\) used for the left graph and \(A-B-C-D-E\) used for the right graph.

As we see in Eq. (2), having a look at the adjacency matrices does not help much. Nevertheless, as already mentioned in the caption of Fig. 3, an isomorphism can be found, mapping the nodes of the right graph onto their corresponding counterparts in the left graph and thus showing that these two graphs are identical according to our definition.

Thus, the task is to find a permutation \(\sigma \) of the nodes in the way that

$$\begin{aligned} \eta _{\textrm{lg}}(\sigma (i),\sigma (j))=\eta _{\textrm{rg}}(i,j) \text{ for } \text{ all } \text{ pairs } \text{ of } \text{ nodes } (i,j). \end{aligned}$$
(3)

So far, there is no exact algorithm solving this problem in polynomial time, although some progress has been made to reduce the computing time needed to find the one correct permutation among the N! possible permutations [21]. However, mostly, there is no need to make use of a brute force attack testing all N! permutations for whether it is the correct one describing an isomorphism between the graphs. Usually, one can make some tricks for significantly reducing the time for finding this permutation or for showing that no such permutation exists. One of these approaches is to consider the degrees \(D_G\) of the various nodes. A node i in graph G has degree

$$\begin{aligned} D_G(i)=\sum _j \eta _G(i,j). \end{aligned}$$
(4)

The degree of a node counts the number of edges attached to this node, i.e., it measures the number of nodes with which it is directly connected via an edge. For our example in Fig. 3, we thus have \(D_{\textrm{lg}}(1)=3\), \(D_{\textrm{lg}}(2)=2\), \(D_{\textrm{lg}}(3)=4\), \(D_{\textrm{lg}}(4)=2\), and \(D_{\textrm{lg}}(5)=3\) for the left graph and \(D_{\textrm{rg}}(A)=3\), \(D_{\textrm{rg}}(B)=2\), \(D_{\textrm{rg}}(C)=2\), \(D_{\textrm{rg}}(D)=3\), and \(D_{\textrm{rg}}(E)=4\) for the right graph. Thus, we already know at this point that the permutation \(\sigma \), if it is to describe an isomorphism, has to map node 3 onto node E, as these are the only nodes with degree 4. Then we can either map node 1 onto node A and 5 onto node D or map node 1 onto node D and 5 onto node A. And analogously we have two possibilities for mapping the nodes with degree 2, we can either map node 2 onto node B and 4 onto node C or map node 2 onto node C and 4 onto node B. Thus, from the original number \(5!=120\) of possible permutations, only \(2\times 2=4\) possible permutations remain which have to be checked whether one of them provides the correct isomorphism.

For bilayer networks comprised of edges connecting droplets filled with different chemicals, the situation is even better. These droplets filled with different chemicals correspond in graph theory to so-called colored nodes. There is a whole bunch of famous problems dealing with colored graphs and graph coloring [22], e.g., the question how many colors are needed at least to color the countries on a map in the way that no two neighboring countries share the same color. While for a globe of the earth and for a map in an atlas, a minimum of four colors is required, seven colors would be needed for the corresponding problem on a torus [23]. If we add the requirement that no two nodes connected by an edge in a bilayer network have the same color, an even larger minimum number of colors could be needed, depending on the network topology.

For our problem of finding out whether two configurations are identical, i.e., whether the underlying bilayer networks can be mapped onto each other by an isomorphism \(\sigma \), we only need to consider those permutations which map the nodes in a way that they stay with the same color, i.e., that they contain the same chemical molecules. Together with approaches like the degree measurement, the computation time needed for finding the isomorphism \(\sigma \) or for proving that the two configurations differ can be strongly reduced.

4 Searching for a Network Core

However, the situation is not so easy. As already mentioned, differences between resulting three-dimensional arrangements can be observed very often, such that it is not too likely that we will one day be able to govern the experiment in a way that all resulting three-dimensional arrangements of droplets share exactly the same underlying bilayer network.

Fig. 4.
figure 4

Simple example for four graphs sharing the same network core but also containing one node attached in various ways to other nodes

Full size image

Instead, we will have to deal with different bilayer networks. In the simplest case, it will be one droplet or a small number of droplets leading to differences between the various resulting networks. As an example, four different possibilities are shown in Fig. 4. In this figure, the new node with No. 6 is located at (almost) the same place in the first three examples, either it is attached to one of the two neighboring nodes or it is even attached to both. But it could also be, as depicted in the fourth example, that such a node is sometimes located at one place and sometimes at another, thus being able to form bilayers with various nodes.

These graphs are of course not identical, no isomorphism exists to map one of these graphs onto another graph, except for the second and the fourth graph between which an isomorphism can be found. Thus, we at first sight seem to be unable to follow the approach described in the last section. Nevertheless, we see that these graphs are almost identical. They share some common core network. The question is how to find out whether networks only differ slightly and share a common core.

One simple approach to this problem of finding a network core was applied by Kirkpatrick and coworkers [24], who simply tried to cut off those network parts which would most likely cause these differences. The idea behind this approach is that the likeliest candidates would be those with minimum degree. For our example in Fig. 4, if we cut off all nodes with degree 1, we would mostly find that the resulting networks share the same core. Only the third example would seemingly have another core. But if we went on also to cut off all nodes with degree 2, then we would e.g. mostly also cut off node No. 2. This shows the limitations of this approach. Another approach suggested by Kirkpatrick would be to successively cut off all nodes with degree 1. Thus in the second iteration of this idea, one would only cut off those nodes which had degree 2 in the original network, but already lost one neighbor which was connected only to it. However, this approach would also not help for resolving the network core in the third example depicted in Fig. 4.

If assuming that the differences between various configurations are indeed so small and of a kind that a common network core exists and can be found, then one still faces the graph isomorphism problem again. However, here an isomorphism has to be found not for the whole graph but only for the assumed network core. If there are larger differences, other strategies, like Searching for Backbones, have to be used which focus on similarities.

5 Searching for Backbones

For various complex optimization problems, like the traveling salesman problem, the vehicle routing problem, and the problem of finding ground states for spin glasses, it has been found that different quasi-optimum configurations share entirely identical backbones [25,26,27,28,29], i.e., parts which are identical in all these configurations.

For finding this backbone summarizing the common parts of different configurations, an overlap measure \(Q(\sigma ,\tau )\) has to be defined. Due to the differences between the various configurations on the one side and the graph isomorphism problem on the other side, we cannot simply make use of the adjacency matrices as in [27] for our bilayer network problem. Instead, here an overlap measure \(Q(\sigma ,\tau )\) would need to count all common properties between the configurations \(\sigma \) and \(\tau \). For example, if both configurations share an edge between a red and a green node, then the overlap is incremented by 1. Of course, such an overlap measure gets maximal if a configuration is compared with itself. However, the various \(Q(\sigma ,\sigma )\) might have slightly different values in our problem, as this approach depends strongly on the number of edges in the bilayer networks, such that the third example in Fig. 4 would have the largest overlap value with itself.

Nevertheless, we could make use of the “aristocratic” approach to the backbone searching problem as described in [29] and only compare those configurations with each other which have large overlap values with each other. Here we would need to study whether all these configurations share a large backbone in the way that some subgraph of the bilayer network is always identical and could be used to perform a gradual reaction scheme for e.g. generating a desired macromolecule. Then one would simply fill all other droplets with e.g. water only, such that they would not disturb the overall reaction processes.

However, it could also turn out that such common properties are not commonly shared among the configurations but that some properties turn up with some larger probabilities, as found for dense packings of multidisperse systems of hard discs [30]. We will see what the outcome of our investigations will be.

6 Ultrametricity

Complex systems often exhibit the property of ultrametricity in configuration space or at least in a subspace of quasi-optimum configurations. As it was also found for a related hard disc packing problem [31], we expect this property also to turn up for this problem.

In order to understand the term ultrametricity, let us first refer to a standard metric. A standard metric like the Euclidean metric is defined as follows:

  • All distances between pairs (i, j) of nodes are nonnegative, i.e., \(d(i,j) \ge 0\) \(\forall (i,j)\).

  • The distance of a node to itself is \(d(i,i)=0\).

  • In the case that a metric is symmetric, we have \(d(i,j)=d(j,i)\) for all pairs of nodes.

  • The most important property of a metric is the triangle inequality: \(d(i,j) \le d(i,k) \,+\, d(k,j)\) for all triples (i, j, k) of nodes, i.e., making a detour via a third node k can never be shorter than traveling directly from i to j.

For an ultrametric, the triangle inequality is replaced by the condition

$$\begin{aligned} d(i,j) \le \textrm{max}\{d(i,k), d(k,j) \} \end{aligned}$$
(5)

for all triples of nodes (i, j, k).

If permuting i, j, k and applying the ultrametricity condition to all permutations, one finds that the nodes have to be placed on triangles which are either equilateral or at least isosceles with short base line, if the ultrametricity condition is fulfilled.

The question is now how to derive distances between bilayer networks. Here we can make use of the overlaps we defined earlier. By normalizing the overlap to

$$\begin{aligned} q_{\sigma \tau }=Q(\sigma ,\tau )/Q_{\textrm{max}}, \end{aligned}$$
(6)

we can e.g. define a distance by

$$\begin{aligned} d(\sigma ,\tau )=1-q_{\sigma \tau }, \end{aligned}$$
(7)

i.e., the larger the overlap is, the smaller is the distance between the corresponding configurations. As demonstrated in [31], the existence of ultrametricity can then be proven by having a look at the joint probability distribution \(p(d(\sigma ,\upsilon ),d(\upsilon ,\tau ))\) for various fixed values of \(d(\sigma ,\tau )\). If this joint probability distribution exhibits when plotted a significant peak along the diagonal and if this signal remains also if subtracting the product of the probabilities for the corresponding distance values, i.e., if considering \(p(d(\sigma ,\upsilon ),d(\upsilon ,\tau ))- p(d(\sigma ,\upsilon )) \times p(d(\upsilon ,\tau ))\), then we find that the system really exhibits the property of ultrametricity.

If this property is fulfilled, then one knows that the resulting three-dimensional arrangements can be gathered in groups, which can be combined to supergroups, those again to hypergroups, and so on. By this successive gathering process, we basically generate an ultrametric tree, which is also well known from other fields of research, like the problem of constructing a phylogenetic tree. In order to construct such a tree, we can make use of the neighbor-joining method, which is a standard tool to reconstruct phylogenetic trees [32, 33]. Another possibility would be to generate a clustered ordering of configurations [34].

7 Replica Symmetry Breaking

Ultrametricity in turn is related to iterated replica symmetry breaking (RSB). In order to derive RSB, let us start off with the replica symmetric assumption. As a simplification, it is assumed that the matrix \((q_{\sigma \tau })\) of normalized overlap values has the form

$$\begin{aligned} (q_{\sigma \tau })=\left( \begin{array}{cccccccccccc} 1 &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q \\ q &{} 1 &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q \\ q &{} q &{} 1 &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q \\ q &{} q &{} q &{} 1 &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q \\ q &{} q &{} q &{} q &{} 1 &{} q &{} q &{} q &{} q &{} q &{} q &{} q \\ q &{} q &{} q &{} q &{} q &{} 1 &{} q &{} q &{} q &{} q &{} q &{} q \\ q &{} q &{} q &{} q &{} q &{} q &{} 1 &{} q &{} q &{} q &{} q &{} q \\ q &{} q &{} q &{} q &{} q &{} q &{} q &{} 1 &{} q &{} q &{} q &{} q \\ q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} 1 &{} q &{} q &{} q \\ q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} 1 &{} q &{} q \\ q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} 1 &{} q \\ q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} q &{} 1 \\ \end{array} \right) , \end{aligned}$$
(8)

i.e., all overlap values between different configurations are equal to one value q with \(0<q<1\). This concept of replica symmetry (RS) is often used in theoretical physics as a first step to approximately calculate some properties [35].

In the next step, one allows for a first breaking of the replica-symmetry (RSB1), such that the overlap matrix e.g. looks like

$$\begin{aligned} (q_{\sigma \tau })=\left( \begin{array}{ccc|ccc|ccc|ccc} 1 &{} q_0 &{} q_0 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 \\ q_0 &{} 1 &{} q_0 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 \\ q_0 &{} q_0 &{} 1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 \\ \hline q_1 &{} q_1 &{} q_1 &{} 1 &{} q_0 &{} q_0 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 \\ q_1 &{} q_1 &{} q_1 &{} q_0 &{} 1 &{} q_0 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 \\ q_1 &{} q_1 &{} q_1 &{} q_0 &{} q_0 &{} 1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 \\ \hline q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} 1 &{} q_0 &{} q_0 &{} q_1 &{} q_1 &{} q_1 \\ q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_0 &{} 1 &{} q_0 &{} q_1 &{} q_1 &{} q_1 \\ q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_0 &{} q_0 &{} 1 &{} q_1 &{} q_1 &{} q_1 \\ \hline q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} 1 &{} q_0 &{} q_0 \\ q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_0 &{} 1 &{} q_0 \\ q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_1 &{} q_0 &{} q_0 &{} 1 \\ \end{array} \right) , \end{aligned}$$
(9)

with two overlap values \(0<q_1<q_0<1\). Thus, we find block matrices with a larger overlap value along the diagonal of the matrix. In the second replica-symmetry breaking step (RSB2), the overlap matrix would e.g. look like

(10)

with three overlap values \(0<q_2<q_1<q_0<1\). Thus, the block matrices along the diagonal are enclosed in even larger block matrices. This approach can be iterated ad infinitum. Using this approach, Parisi was able to find the minimum energy for the Sherrington-Kirkpatrick spin glass model [36, 37]. By using the clustering approach as described in [34], we could also try to find an ordering among the various different three-dimensional arrangements of droplets, such that an overlap matrix could look this way. Then we would know that we have groups of resulting bilayer configurations which have many properties in common or that we even have groups of configurations which allow for a small number of parallel evolving successive chemical reaction schemes.

8 Summary and Outlook

Within the European Horizon 2020 project ACDC, we aim at the development of a chemical compiler being able to govern biochemical reactions in a cheap and portable biochemical laboratory, intended to e.g. create specific macromolecules, like antibiotics. For this purpose, a microfluidic system is used in which droplets are generated which arrange themselves in a three-dimensional way and form bilayers with neighboring droplets. These bilayers form a network which can be used for some specific successive biochemical reaction scheme. Besides trying to understand and to simulate this spatial transition [4] in order to foretell the experimental outcome, we also have to investigate the final droplet arrangements and their corresponding bilayer networks, achieved in experiments and from computer simulations, in order to later on be able to design experiments in a way that some specific bilayer networks are created being able to produce the macromolecules desired.

In this paper, we have dwelt on thoughts about how to characterize differences between various three-dimensional agglomerations of droplets and their corresponding bilayer networks. If there are only small and few differences, searching for a network core might be a suitable strategy. Then all the configurations exhibit the same core network, which can then be used for the reaction scheme instead of the overall network. If this strategy is not successful, we can use the Searching for Backbones algorithm in order to detect parts which are common to all configurations and then determine whether it is possible to use the various ways in which these common parts are connected in the various bilayer networks in order to create the desired macromolecules. But if comparing all configurations in parallel, one might overlook that there might be groups consisting of configurations which are rather similar to each other within each group but exhibit larger differences to configurations in other groups. It might even be that not only various configurations can be merged to groups but that we can iterate this strategy, thus finding supergroups and hypergroups. For various complex problems, such successive mergings of configurations have already been detected by investigating ultrametric properties and replica symmetry breaking, which we also intend to use.

If we have been able to create configurations in Monte Carlo simulations similar to those found in experiments and even to foretell which configurations will be created if changing the experimental situation as described in [4], and if we have achieved this second part of our objective of understanding and predicting the outcome of an experimental setup, i.e., the various groups of three-dimensional arrangements of droplets generated, then we will be able to create a probabilistic chemical compiler in the final stage of this project. We aim at creating plans for e.g. a step-wise generation of some desired macromolecules, which are gradually constructed from smaller units, being contained in the various droplets, with the successive chemical reactions being enabled via the bilayers formed between neighboring droplets. Such a compiler has been exemplarily already developed for one specific molecule [2]. In this project, this compiler has to be generalized and also made probabilistic because of the variability in the rearrangement process which is to be expected.