Abstract
Currently, lattice-based cryptosystems are less efficient than their number-theoretic counterparts (based on RSA, discrete logarithm, etc.) in terms of key and ciphertext (signature) sizes. For adequate security the former typically needs thousands of bytes while in contrast the latter only requires at most hundreds of bytes. This significant difference has become one of the main concerns in replacing currently deployed public-key cryptosystems with lattice-based ones. Observing the inherent asymmetries in existing lattice-based cryptosystems, we propose asymmetric variants of the (module-)LWE and (module-)SIS assumptions, which yield further size-optimized KEM and signature schemes than those from standard counterparts.
Following the framework of Lindner and Peikert (CT-RSA 2011) and the Crystals-Kyber proposal (EuroS&P 2018), we propose an IND-CCA secure KEM scheme from the hardness of the asymmetric module-LWE (AMLWE), whose asymmetry is fully exploited to obtain shorter public keys and ciphertexts. To target at a 128-bit quantum security, the public key (resp., ciphertext) of our KEM only has 896 bytes (resp., 992 bytes).
Our signature scheme bears most resemblance to and improves upon the Crystals-Dilithium scheme (ToCHES 2018). By making full use of the underlying asymmetric module-LWE and module-SIS assumptions and carefully selecting the parameters, we construct an SUF-CMA secure signature scheme with shorter public keys and signatures. For a 128-bit quantum security, the public key (resp., signature) of our signature scheme only has 1312 bytes (resp., 2445 bytes).
We adapt the best known attacks and their variants to our AMLWE and AMSIS problems and conduct a comprehensive and thorough analysis of several parameter choices (aiming at different security strengths) and their impacts on the sizes, security and error probability of lattice-based cryptosystems. Our analysis demonstrates that AMLWE and AMSIS problems admit more flexible and size-efficient choices of parameters than the respective standard versions.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Despite the tremendous success of traditional public-key cryptography (also known as asymmetric-key cryptography), the typical public-key cryptosystems in widespread deployment on the Internet are based on number-theoretic hardness assumptions such as factoring and discrete logarithms, and thus are susceptible to quantum attacks [31] if large-scale quantum computers become a reality. With the advancement of quantum computing technology in recent years [19], developing post-quantum cryptography (PQC) with resistance to both classical and quantum computers has become a primary problem as well as a priority issue for the crypto community. Actually, several government agencies and standardization organizations have announced plans to solicit and standardize PQC algorithms. In 2015, the NSA [28] has announced its schedule for migration to PQC. In 2016, the NIST initiated its standardization process for post-quantum public-key encryption (PKE), key-establishment (KE) and digital signatures. Among the 69 PQC submissions received worldwide, 17 candidate PKE and KE algorithms (e.g., Kyber [6]), and 9 candidate signature schemes (e.g., Dilithium [12]) have been selected to the 2nd round of the NIST PQC standardization, where 12 out of the total 26 2nd-round candidates are lattice-based algorithms.
Most lattice-based cryptosystems base their security on the conjectured quantum hardness of the Short Integer Solution (SIS) problem [1, 27] and the Learning With Errors (LWE) problem [30]. Informally speaking, the two problems are both related to solving systems of linear congruences (and are in some sense dual to each other). Let n, m, q be integers and \(\alpha \), \(\beta \) be reals, and let \(\chi _\alpha \) be some distribution (e.g., a Gaussian distribution) with parameter \(\alpha \) defined over \(\mathbb {Z}\). The SIS problem \(\mathrm {SIS}^\infty _{n,m,q,\beta }\) in the infinity norm asks to find out a non-zero vector \(\mathbf {x}\in \mathbb {Z}^m\), given a random matrix \({\mathbf {A}}\xleftarrow {\$}\mathbb {Z}_q^{n\times m}\), such that \({\mathbf {A}}\mathbf {x}= \mathbf {0}\bmod q\) and \(\Vert \mathbf {x}\Vert _\infty \le \beta \). Correspondingly, the search LWE problem \(\mathrm {LWE}_{n,m,q,\alpha }\) searches for \(\mathbf {s}\in \mathbb {Z}_q^n\) from samples \(({\mathbf {A}},\mathbf {b}= {\mathbf {A}}\mathbf {s}\,+\,\mathbf {e})\in \mathbb {Z}_q^{m\times n } \times \mathbb {Z}_q^m\), where \({\mathbf {A}}\xleftarrow {\$}\mathbb {Z}_q^{m\times n}\), \(\mathbf {s}\xleftarrow {\$}\mathbb {Z}_q^n\) and \(\mathbf {e}\xleftarrow {\$}\chi _\alpha ^m\). Decisional LWE problem asks to distinguish \(({\mathbf {A}},\mathbf {b}= {\mathbf {A}}\mathbf {s}\, +\,\mathbf {e})\) from uniform distribution over \(\mathbb {Z}_q^{m\times n} \times \mathbb {Z}_q^m\). For certain parameters the two (search and decisional) LWE problems are polynomially equivalent [25, 30].
It has been shown that the two average-case problems SIS and LWE are at least as hard as some worst-case lattice problems (e.g., Gap-SIVP) for certain parameter choices [27, 30]. Moreover, quantum algorithms are not known to have substantial advantages (beyond polynomial speedup) over classical ones in solving these problems, which makes SIS and LWE ideal candidates for post-quantum cryptography. We mention a useful variant of LWE, called the (Hermite) normal form of LWE, where the secret \(\mathbf {s}\) is sampled from noise distribution \(\chi _\alpha ^n\) (instead of uniform). The standard LWE and its normal form were known to be equivalent up to a polynomial number of samples [4]. Furthermore, the use of a “small” secret in LWE comes in handy in certain application scenarios, e.g., for better managing the growth of the noise in fully homomorphic encryption [7, 10].
SIS is usually used in constructing signature schemes, and LWE is better suited for PKE schemes. However, the standard LWE and SIS problems seem to suffer some constraints in choosing parameters for some practical cryptographic schemes. For example, the LWE parameter for achieving a 128-bit (quantum) security typically cannot provide a matching decryption failure probability \(\nu \) (say \(\nu =2^{-128}\)) for the resulting LWE-based PKE scheme. Note that a larger \(\nu \) (i.e., \(\nu > 2^{-128}\)) may sacrifice the security, and a smaller \(\nu \) (i.e., \(\nu < 2^{-128}\)) may compromise the performance. To this end, we introduce special variants of SIS and LWE, referred to as asymmetric SIS (ASIS) and asymmetric LWE (ALWE).
Informally, the ASIS problem \(\mathrm {ASIS}^\infty _{n,m_1,m_2,q,\beta _1,\beta _2}\) refers to the problem that, given a random \({\mathbf {A}}\xleftarrow {\$}\mathbb Z_q^{n\times (m_1+m_2)}\), find out a non-zero \(\mathbf {x}=(\mathbf {x}_1^T,\mathbf {x}_2^T)^T\in \mathbb Z^{m_1+m_2}\) satisfying \({\mathbf {A}}\mathbf {x}= \mathbf {0}\bmod q\), \(\Vert \mathbf {x}_1\Vert _\infty \le \beta _1\) and \(\Vert \mathbf {x}_2\Vert _\infty \le \beta _2\). It is easy to see that \(\mathrm {ASIS}^\infty _{n,m_1,m_2,q,\beta _1,\beta _2}\) is at least as hard as \(\mathrm {SIS}^\infty _{n,m_1+m_2,q,\max (\beta _1,\beta _2)}\). Thus, we have
This lays the theoretical foundation for constructing secure signatures based on the ASIS problem. In addition, we investigate a class of algorithms for solving the ASIS problem, and provide a method for selecting appropriate parameters for different security levels with reasonable security margin.
Correspondingly, the ALWE problem \(\mathrm {ALWE}_{n,m,q,\alpha _1,\alpha _2}\) asks to find out \(\mathbf {s}\in \mathbb Z_q^n\) from samples \(({\mathbf {A}},\mathbf {b}= {\mathbf {A}}\mathbf {s}\, +\,\mathbf {e})\in \mathbb Z_q^{m\times n } \times \mathbb Z_q^m\), where \({\mathbf {A}}\xleftarrow {\$}\mathbb Z_q^{m\times n},\mathbf {s}\xleftarrow {\$}\chi _{\alpha _1}^n, \mathbf {e}\xleftarrow {\$}\chi _{\alpha _2}^m\). The hardness of ALWE may depend on the actual distribution from which \(\mathbf {s}\) (or \(\mathbf {e}\)) is sampled, and thus we cannot simply compare the hardness of LWE and ALWE like we did for SIS and ASIS. However, the relation below remains valid for our parameter choices in respect to all known solving algorithms despite the lack of a proof in general:Footnote 1
More importantly, the literature [9, 16, 26] suggests that ALWE can reach comparable hardness to standard LWE as long as the secret is sampled from a distribution (i.e., \(\chi _{\alpha _1}^n\)) with sufficiently large entropy (e.g., uniform distribution over \( \{0, 1\}^{n} \)) and appropriate values are chosen for other parameters. This shows the possibility of constructing secure cryptographic schemes based on the ALWE problem. We also note that Cheon et al. [11] introduced a variant of LWE that is quite related to ALWE, where \(\mathbf {s}\) and \(\mathbf {e}\) are sampled from different distributions (notice that \(\mathbf {s}\) and \(\mathbf {e}\) in the ALWE problem are sampled from the same distribution \(\chi \), albeit with different parameters \(\alpha _1\) and \(\alpha _2\)). By comprehensively comparing, analyzing and optimizing the state-of-the-art LWE solving algorithms, we establish approximate relations between parameters of ALWE and LWE, and suggest practical parameter choices for several levels of security strength intended for ALWE.
The definitions of the aforementioned variants can be naturally generalized to the corresponding ring and module versions, i.e., ring-LWE/SIS and module-LWE/SIS. As exhibited in [6, 12], module-LWE/SIS allows for better trade-off between security and performance. We will use the asymmetric module-LWE problem (AMLWE) and the asymmetric module-SIS problem (AMSIS) to build a key encapsulation mechanism (KEM) and a signature scheme of smaller sizes.
Technically, our KEM scheme is mainly based on the PKE schemes in [6, 22], except that we make several modifications to utilize the inherent asymmetry of the (M)LWE secret and noise in contributing to the decryption failure probabilities, which allow us to obtain smaller public keys and ciphertexts. In Sect. 3.1, we will further discuss this asymmetry in the design of existing schemes, and illustrate our design rationale in more details. For a targeted 128-bit security, the public key (resp., ciphertext) of our KEM only has 896 bytes (resp., 992 bytes).
Our signature scheme bears most resemblance to Dilithium in [12]. The main difference is that we make several modifications to utilize the asymmetric parameterization of the (M)LWE and (M)SIS to reach better trade-offs among computational costs, storage overhead and security, which yields smaller public keys and signatures without sacrificing the security or computational efficiency. In Sect. 4.1, we will further discuss the asymmetries in existing constructions, and illustrate our design rationale in more details. For a targeted 128-bit quantum security, the public key (resp., signature) of our signature scheme only has 1312 bytes (resp., 2445 bytes).
We make a comprehensive and in-depth study on the concrete hardness of AMLWE and AMSIS by adapting the best known attacks (that were originally intended for MLWE and MSIS respectively) and their variants (that were modified to solve AMLWE and AMSIS respectively), and provide several choices of parameters for our KEM and signature schemes aiming at different security strengths. The implementation of our schemes (and its comparison with the counterparts) confirms that our schemes are practical and competitive. We compare our KEM with NIST round2 lattice-based PKEs/KEMs in Sect. 1.1, and compare our signature with NIST round2 lattice-based signatures in Sect. 1.2.
1.1 Comparison with NIST Round2 Lattice-Based PKEs/KEMs
As our KEM is built upon Kyber [6], we would like to first give a slightly detailed comparison between our KEM and Kyber-round2 [6] in Table 1. Our software is implemented in C language with optimized number theory transform (NTT) and vector multiplication using AVX2 instructions. The running times of \(\mathsf{KeyGen}\), \(\mathsf{Encap}\) and \(\mathsf{Decap}\) algorithms are measured in averaged CPU cycles of 10000 times running on a 64-bit Ubuntu 14.4 LTS ThinkCenter desktop (equipped with Intel Core-i7 4790 3.6 GHz CPU and 4 GB memory). The sizes of public key |pk|, secret key |sk|, ciphertext |C| are measured in terms of bytes. The column |ss| gives the size of the session key that is encapsulated by each ciphertext. The column “Dec. Failure” lists the probabilities of decryption failure. The last column “Quant. Sec.” gives the estimated quantum security level expressed in bits.
Note that for \(X \in \{512, 768, 1024\}\) aiming at NIST Category I, III and V, the estimated quantum security of our KEM \({\varPi }_{\text {KEM}}\)-X is slightly lower than that of Kyber-X, but we emphasize that our parameter choices have left out sufficient security margin reserved for further development of attacks. For example, our \({\varPi }_{\text {KEM}}\)-768 reaches an estimated quantum security of 147 bits and a \(2^{-128}\) decryption failure probability, which we believe is sufficient to claim the same targeted 128-bit quantum security (i.e., NIST Category III) as Kyber-768. We also note that the parameter choice of \({\varPi }_{\text {KEM}}\)-1024 is set to encapsulate a 64-byte session key, which is twice the size of that achieved by Kyber-1024. This decision is based on the fact that a 32-byte session key may not be able to provide a matching security strength, say, more than 210-bit quantum security (even if the Grover algorithm [17] cannot provide a real quadratic speedup over classical algorithms in practice).
We note that the Kyber team [6] removed the public-key compression to purely base their Kyber-round2 scheme on the standard MLWE problem and obtained (slightly) better computational efficiency (for saving several operations such as NTT). On the first hand, as commented by the Kyber team that “we strongly believe that this didn’t lower actual security”, we prefer to use the public-key compression to obtain smaller public key sizes (with the cost of a slightly worse computational performance). On the other hand, one can remove the public-key compression and still obtain a scheme with shorter ciphertext size (see \({\varPi }_{\text {KEM}}\)-X\(^\dagger \) in Table 1), e.g., a reduction of 128 bytes in the ciphertext size over Kyber-768 at the targeted 128-bit quantum security by using a new parameter set \((n,k,q,\eta _1,\eta _2,d_u, d_v)=(256,3,3329,1,2,9,3)\) (see \({\varPi }_{\text {KEM}}\)-X\(^\dagger \) in Table 5).
We also give a comparison between our KEM and NIST round2 lattice-based PKEs/KEMs in Table 2. For simplicity, we only compare those schemes under the parameter choices targeted at IND-CCA security and 128-bit quantum security in terms of space and time (measured in averaged CPU cycles of running 10000 times) on the same computer. We failed to run the softwares of the schemes marked with ‘\(^*\)’ on our experiment computer (but a public evaluation on the Round1 submissions suggests that Three-Bears may have better computational efficiency than Kyber and ours). As shown in Table 2, our \({\varPi }_{\text {KEM}}\) has a very competitive performance in terms of both sizes and computational efficiency.
1.2 Comparison with NIST Round2 Lattice-Based Signatures
We first give a slightly detailed comparison between our signature \(\varPi _{\mathrm {SIG}}\) with Dilithium-round2 [12] in Table 3. Similarly, the running times of the \(\mathsf{KeyGen}\), \(\mathsf{Sign}\) and \(\mathsf{Verify}\) algorithms are measured in the average number of CPU cycles (over 10000 times) on the same machine configuration as before. The sizes of public key |pk|, secret key |sk|, signature \(|\sigma |\) are counted in bytes. As shown in Table 3, the estimated quantum security of \({\varPi }_{{\text {SIG}}}\)-1024 is slightly lower than that of Dilithium-1024, but those at \({\varPi }_{{\text {SIG}}}\)-1280 and \({\varPi }_{{\text {SIG}}}\)-1536 are slightly higher. In all, our scheme has smaller public key and signatures while still providing comparable efficiency to (or even slightly faster than) Dilithium-round2.
We also compare our signature with NIST round2 lattice-based signatures: Falcon, qTESLA and Dilithium, where the first one is an instantiation of full-domain hash and trapdoor sampling [15] on NTRU lattices (briefly denoted as FDH-like methodology), and the last two follows the more efficient Fiat-Shamir heuristic with rejection sampling (briefly denoted as FS-like methodology) [24]. As we failed to run the softwares of Falcon and qTESLA on our experiment computer (but a public evaluation on the round1 submissions suggests that Falcon and qTESLA are probably much slower than Dilithium), we only compare the sizes of those schemes at all parameter choices in Table 4. Note that the qTESLA team had dropped all the parameter sets of qTESLA-round2, the figures in Table 4 corresponds to their new choices of parameter sets.
1.3 Organizations
Section 2 gives the preliminaries and background information. Section 3 describes the KEM scheme from AMLWE. Section 4 presents the digital signature scheme from AMLWE and AMSIS. Section 5 analyzes the concrete hardness of AMLWE and AMSIS by adapting the best known attacks.
2 Preliminaries
2.1 Notation
We use \(\kappa \) to denote the security parameter. For a real number \(x \in \mathbb {R}\), \({\lceil }{x}{\rfloor }\) denotes the closest integer to x (with ties being rounded down, i.e., \({\lceil }{0.5}{\rfloor } = 0\)). We denote by R the ring \(R=\mathbb {Z}[X]/(X^n+1)\) and by \(R_q\) the ring \(R_q=\mathbb {Z}_q[X]/(X^n+1)\), where n is a power of 2 so that \(X^n+1\) is a cyclotomic polynomial. For any positive integer \(\eta \), \(S_\eta \) denotes the set of ring elements of R that each coefficient is taken from \(\{-\eta ,-\eta +1 \dots , \eta \}\). The regular font letters (e.g., a, b) represent elements in R or \(R_q\) (including elements in \(\mathbb {Z}\) or \(\mathbb {Z}_q\)), and bold lower-case letters (e.g., \(\mathbf{a}\), \(\mathbf{b}\)) denote vectors with coefficients in R or \(R_q\). By default, all vectors will be column vectors. Bold upper-case letters (e.g., \(\mathbf{A}\), \(\mathbf{B}\)) represent matrices. We denote by \({\mathbf{a}}^T\) and \({\mathbf{A}}^T\) the transposes of vector \(\mathbf{a}\) and matrix \(\mathbf{A}\) respectively.
We denote by \(x\xleftarrow {\$}D\) sampling x according to a distribution D and by \(x\xleftarrow {\$}S\) denote sampling x from a set S uniformly at random. For two bit-strings s and t, \(s\Vert t\) denotes the concatenation of s and t. We use \(\log _b\) to denote the logarithm function in base b (e.g., 2 or natural constant e) and \(\log \) to represent \(\log _e\). We say that a function \(f: \mathbb {N} \rightarrow [0,1]\) is negligible, if for every positive c and all sufficiently large \(\kappa \) it holds that \(f(\kappa ) < 1/\kappa ^c\). We denote by \(\mathsf{negl}:\mathbb {N} \rightarrow [0,1]\) an (unspecified) negligible function. We say that f is overwhelming if \(1-f\) is negligible.
2.2 Definitions
Modular Reductions. For an even positive integer \(\alpha \), we define \(r' = r \ \text {mod}^{\pm }\ \alpha \) as the unique element in the range \((-\frac{\alpha }{2}, \frac{\alpha }{2}]\) such that \(r' = r \bmod \alpha \). For an odd positive integer \(\alpha \), we define \(r' = r \ \text {mod}^{\pm }\ \alpha \) as the unique element in the range \([-\frac{\alpha \,-\,1}{2}, \frac{\alpha \,-\,1}{2}]\) such that \(r' = r \bmod \alpha \). For any positive integer \(\alpha \), we define \(r' = r \ \text {mod}^{+}\ \alpha \) as the unique element in the range \([0, \alpha )\) such that \(r' = r \bmod \alpha \). When the exact representation is not important, we simply write \(r \bmod \alpha \).
Sizes of Elements. For an element \(w \in \mathbb {Z}_q\), we write \(\Vert w\Vert _{\infty }\) to mean \(|w \ \text {mod}^{\pm }\ q|\). The \(\ell _{\infty }\) and \(\ell _2\) norms of a ring element \(w=w_0+w_1X+\dots + w_{n-1}X^{n-1}\in R\) are defined as follows:
Similarly, for \({\mathbf{w}}=(w_1, \dots , w_k)\in R^k\), we define
Modulus Switching. For any positive integers p, q, we define the modulus switching function \({\lceil }{\cdot }{\rfloor }_{q\rightarrow p}\) as:
It is easy to show that for any \(x \in \mathbb {Z}_q\) and \(p<q\in \mathbb {N}\), \(x' = {\lceil }{{\lceil }{x}{\rfloor }_{q\rightarrow p}}{\rfloor }_{p\rightarrow q}\) is an element close to x, i.e,
When \({\lceil }{\cdot }{\rfloor }_{q\rightarrow p}\) is used to a ring element \(x \in R_q\) or a vector \({\mathbf{x}}\in R_q^k\), the procedure is applied to each coefficient individually.
Binomial Distribution. The centered binomial distribution \(B_\eta \) with some positive integer \(\eta \) is defined as follows:
When we write that sampling a polynomial \(g \xleftarrow {\$}B_{\eta }\) or a vector of such polynomials \(\mathbf{g} \xleftarrow {\$}B_{\eta }\), we mean that sampling each coefficient from \(B_{\eta }\) individually.
2.3 High/Low Order Bits and Hints
Our signature scheme will adopt several simple algorithms proposed in [12] to extract the “higher-order” bits and “lower-order” bits from elements in \(\mathbb {Z}_q\). The goal is that given an arbitrary element \(r\in \mathbb {Z}_q\) and another small element \(z \in \mathbb {Z}_q\), we would like to recover the higher order bits of \(r+z\) without needing to store z. Ducas et al. [12] define algorithms that take r, z and generate a 1-bit hint h that allows one to compute the higher order bits of \(r+z\) just using r and h. They consider two different ways which break up elements in \(\mathbb {Z}_q\) into their “higher-order” bits and “lower-order” bits. The related algorithms are described in Algorithms 1–6. We refer the reader to [12] for the illustration of the algorithms.
The following lemmas claim some crucial properties of the above supporting algorithms, which are necessary for the correctness and security of our signature scheme. We refer to [12] for their proofs.
Lemma 1
Let q and \(\alpha \) be positive integers such that \(q> 2\alpha \), \(q \bmod \alpha =1\) and \(\alpha \) is even. Suppose that \(\mathbf {r},\mathbf {z}\) are vectors of elements in \(R_q\), where \({\Vert }{\mathbf {z}}{\Vert }_\infty \le \alpha /2\). Let \(\mathbf{h},\mathbf{h}'\)be vectors of bits. Then, algorithms \(\mathsf{HighBits}_q\), \(\mathsf{MakeHint}_q\) and \(\mathsf{UseHint}_q\) satisfy the following properties:
-
\(\mathsf{UseHint}_q(\mathsf{MakeHint}_q(\mathbf {z},\mathbf {r},\alpha ),\mathbf {r},\alpha ) = \mathsf{HighBits}_q(\mathbf {r}+ \mathbf {z}, \alpha )\).
-
Let \(\mathbf {v}_1 = \mathsf{UseHint}_q(\mathbf{h},\mathbf {r},\alpha )\). Then \({\Vert }{\mathbf {r}- \mathbf {v}_1\cdot \alpha }{\Vert }_\infty \le \alpha +1\). Furthermore, if the number of 1’s in \(\mathbf{h}\) is at most \(\omega \), then all except for at most \(\omega \) coefficients of \(\mathbf {r}- \mathbf {v}_1 \cdot \alpha \) will have magnitude at most \(\alpha /2\) after centered reduction modulo q.
-
For any \(\mathbf{h}, \mathbf{h}'\), if \(\mathsf{UseHint}_q(\mathbf{h}, \mathbf{r}, \alpha )=\mathsf{UseHint}_q(\mathbf{h}', \mathbf{r}, \alpha )\), then \(\mathbf{h}=\mathbf{h}'\).
Lemma 2
If \({\Vert }{\mathbf{s}}{\Vert }_\infty \le \beta \) and \({\Vert }{\mathsf{LowBits}_q(\mathbf {r},\alpha )}{\Vert }_\infty < \alpha /2 -\beta \), then we have:






3 An Improved KEM from AMLWE
Our scheme is based on the key encapsulation mechanism in [6, 22]. The main difference is that our scheme uses a (slightly) different hardness problem, which gives us a flexible way to set the parameters for both performance and security.
3.1 Design Rationale
For simplicity and clarity, we explain the core idea using the (A)LWE-based public-key encryption (PKE) scheme as an example. Note that most LWE-based PKE schemes mainly follow the framework in [22] up to the choices of parameters and noise distributions. Let \(n,q\in \mathbb {Z}\) be positive integers, and let \(\chi _\alpha \subset \mathbb {Z}\) be a discrete Gaussian distribution with standard variance \(\alpha \in \mathbb {R}\). The LWE-based PKE works as follows:
-
Key generation: randomly choose \({\mathbf {A}}\xleftarrow {\$}\mathbb {Z}_q^{n\times n}\), \(\mathbf {s},\mathbf {e}\xleftarrow {\$}\chi _\alpha ^n\) and compute \(\mathbf {b}= {\mathbf {A}}\mathbf {s}+ \mathbf {e}\). Return the public key \(pk = ({\mathbf {A}},\mathbf {b})\) and secret key \(sk = \mathbf {s}\).
-
Encryption: given the public key \(pk = ({\mathbf {A}},\mathbf {b})\) and a plaintext \(\mu \in \{0, 1\}^{} \), randomly choose \(\mathbf {r},\mathbf {x}_1\xleftarrow {\$}\chi _\alpha ^n,x_2 \xleftarrow {\$}\chi _\alpha \) and compute \(\mathbf {c}_1= {\mathbf {A}}^T \mathbf {r}+ \mathbf {x}_1\), \(c_2 = \mathbf {b}^T \mathbf {r}+ x_2 + \mu \cdot {\lceil }{\frac{q}{2}}{\rfloor }\). Finally, return the ciphertext \(C=(\mathbf {c}_1,c_2)\).
-
Decryption: given the secret key \(sk = \mathbf {s}\) and a ciphertext \(C=(\mathbf {c}_1,c_2)\), compute \(z= c_2 - \mathbf {s}^T\mathbf {c}_1\) and output \({\lceil }{z\cdot \frac{2}{q}}{\rfloor } \bmod 2\) as the decryption result.
For a honestly generated ciphertext \(C=(\mathbf {c}_1,c_2)\) that encrypts plaintext \(\mu \in \{0, 1\}^{} \), we have:

Thus, the decryption algorithm is correct as long as \({|}{e'}{|}<\frac{q}{4}\). Since \({|}{x_2}{|}\ll {|}{\mathbf {e}^T \mathbf {r}- \mathbf {s}^T \mathbf {x}_1}{|}\), the magnitude of \({|}{e'}{|}\) mainly depends on \({|}{\mathbf {e}^T \mathbf {r}- \mathbf {s}^T \mathbf {x}_1}{|}\). That is, the LWE secret \((\mathbf {s},\mathbf {r})\) and the noise \((\mathbf {e},\mathbf {x}_1)\) contribute almost equally to the magnitude of \({|}{e'}{|}\). Moreover, for a fixed n the expected magnitude of \({|}{\mathbf {e}^T \mathbf {r}- \mathbf {s}^T \mathbf {x}_1}{|}\) is a monotonically increasing function of \(\alpha \):
Let \(\nu \) be the probability that the decryption algorithm fails, and let \(\lambda \) be the complexity of solving the underlying LWE problem. Ideally, for a targeted security strength \(\kappa \), we hope that \(\nu = 2^{-\kappa }\) and \(\lambda = 2^\kappa \), since a large \(\nu \) (i.e., \(\nu > 2^{-\kappa }\)) will sacrifice the overall security, and a large \(\lambda \) (i.e., \(\lambda > 2^\kappa \)) may compromise the overall performance. Since both \(\nu \) and \(\lambda \) are strongly related to the ratio \(\alpha /q\) of the Gaussian parameter \(\alpha \) and the modulus q, it is hard to come up with an appropriate choice of \((\alpha ,q)\) to simultaneously achieve the best of the two worlds.
To obtain smaller public keys and ciphertexts (and thus improve the communication efficiency), many schemes use the modulus switching technique [8, 10] to compress public keys and ciphertexts. We refer to the following scheme that adopts modulus switching technique to compress public keys and ciphertexts, where \(p_1,p_2,p_3\in \mathbb {Z}\) are parameters for compression (\(p_1\) for the public key and \(p_2,p_3\) for ciphertexts).
-
Key generation: pick \({\mathbf {A}}\xleftarrow {\$}\mathbb {Z}_q^{n\times n}\) and \(\mathbf {s},\mathbf {e}\xleftarrow {\$}\chi _\alpha ^n\) and compute \(\mathbf {b}= {\mathbf {A}}\mathbf {s}+ \mathbf {e}\). Then, return the public key \(pk = ({\mathbf {A}},\bar{\mathbf {b}} = {\lceil }{\mathbf {b}}{\rfloor }_{q\rightarrow p_1})\) and the secret key \(sk = \mathbf {s}\).
-
Encryption: given the public key \(pk = ({\mathbf {A}},\bar{\mathbf {b}})\) and a plaintext \(\mu \in \{0, 1\}^{} \), randomly choose \(\mathbf {r},\mathbf {x}_1\xleftarrow {\$}\chi _\alpha ^n,x_2 \xleftarrow {\$}\chi _\alpha \), and compute \(\mathbf {c}_1= {\mathbf {A}}^T \mathbf {r}+ \mathbf {x}_1\) and \(c_2 = {\lceil }{\bar{\mathbf {b}}}{\rfloor }_{p_1\rightarrow q}^T \mathbf {r}+ x_2 + \mu \cdot {\lceil }{\frac{q}{2}}{\rfloor }\). Return the ciphertext \(C=(\bar{\mathbf {c}}_1={\lceil }{\mathbf {c}_1}{\rfloor }_{q\rightarrow p_2},\bar{\mathbf {c}}_2={\lceil }{c_2}{\rfloor }_{q\rightarrow p_3})\).
-
Decryption: given the secret key \(sk = \mathbf {s}\) and a ciphertext \(C=(\bar{\mathbf {c}}_1,\bar{\mathbf {c}}_2)\), compute \(z = {\lceil }{\bar{\mathbf {c}}_2}{\rfloor }_{p_3\rightarrow q} - \mathbf {s}^T{\lceil }{\bar{\mathbf {c}}_1}{\rfloor }_{p_2\rightarrow q}\) and output \( {\lceil }{z}{\rfloor }_{q\rightarrow 2} = {\lceil }{z\cdot \frac{2}{q}}{\rfloor } \bmod 2\) as the decryption result.
Let
It is easy to verify \({\Vert }{\bar{\mathbf {e}}}{\Vert }_\infty \le \frac{q}{2p_1},{\Vert }{\bar{\mathbf {x}}_1}{\Vert }_\infty \le \frac{q}{2p_2}\), and \({|}{\bar{x}_2}{|} \le \frac{q}{2p_3}\). For any valid ciphertext \(C=(\bar{\mathbf {c}}_1,\bar{\mathbf {c}}_2)\) that encrypts \(\mu \in \{0, 1\}^{} \) we have

Apparently, the smaller values for \(p_1,p_2,p_3\) the better compression rate is achieved for public keys and ciphertexts. At the same time, however, by the definitions of \(\bar{\mathbf {e}},\bar{\mathbf {x}}_1,\bar{x}_2\) we know that smaller \(p_1,p_2,p_3\) also result in a larger noise \(e'\). Notice that when \(p_1,p_2,p_3\) are much smaller than q, we will have \({\Vert }{\bar{\mathbf {e}}}{\Vert }_\infty \gg {\Vert }{\mathbf {e}}{\Vert }_\infty \), \({\Vert }{\bar{\mathbf {x}}_1}{\Vert }_\infty \gg {\Vert }{\mathbf {x}_1}{\Vert }_\infty \) and \({|}{\bar{x}_2}{|} \gg {|}{x_2}{|}\), which further leads to asymmetric roles of \((\mathbf {e},\mathbf {x}_1,x_2)\) and \((\mathbf {s},\mathbf {r})\) in contributing to the resulting size of \({|}{e'}{|}\), i.e., for specific \((p_1,p_2,p_3)\) decreasing (resp., increasing) \({\Vert }{\mathbf {s}}{\Vert }_\infty \) or \({\Vert }{\mathbf {r}}{\Vert }_\infty \) would significantly reducing (resp., enlarging) the noise \({|}{e'}{|}\), and in contrast, changing the size of \({\Vert }{\mathbf {e}}{\Vert }_\infty ,{\Vert }{\mathbf {x}_1}{\Vert }_\infty \) and \({|}{x_2}{|}\) would not result in substantial change to \({|}{e'}{|}\).
The asymmetry observed above motivates the design of our ALWE-based PKE, which uses different noise distributions \(\chi _{\alpha _1}\) and \(\chi _{\alpha _2}\) (i.e., same distribution with different parameters \(\alpha _1\) and \(\alpha _2\)) for the secrets (i.e., \(\mathbf {s}\) and \(\mathbf {r}\)) and the errors (i.e., \(\mathbf {e},\mathbf {x}_1,x_2\)), respectively.
-
Key generation: pick \({\mathbf {A}}\xleftarrow {\$}\mathbb {Z}_q^{n\times n}\), \(\mathbf {s}\xleftarrow {\$}\chi _{\alpha _1}^n\) and \(\mathbf {e}\xleftarrow {\$}\chi _{\alpha _2}^n\), compute \(\mathbf {b}={\mathbf {A}}\mathbf {s}+ \mathbf {e}\). Then, return the public key \(pk = ({\mathbf {A}},\bar{\mathbf {b}} = {\lceil }{\mathbf {b}}{\rfloor }_{q\rightarrow p_1})\) and the secret key \(sk = \mathbf {s}\).
-
Encryption: given the public key \(pk = ({\mathbf {A}},\bar{\mathbf {b}})\) and a plaintext \(\mu \in \{0, 1\}^{} \), randomly choose \(\mathbf {r}\xleftarrow {\$}\chi _{\alpha _1}^n,\mathbf {x}_1\xleftarrow {\$}\chi _{\alpha _2}^n,x_2 \xleftarrow {\$}\chi _{\alpha _2}\), compute \(\mathbf {c}_1 = {\mathbf {A}}^T \mathbf {r}+ \mathbf {x}_1\) and \(c_2= {\lceil }{\mathbf {b}}{\rfloor }_{p_1\rightarrow q}^T \mathbf {r}\) + \(x_2\) + \(\mu \cdot {\lceil }{\frac{q}{2}}{\rfloor }\), and return the ciphertext \(C=(\bar{\mathbf {c}}_1={\lceil }{\mathbf {c}_1}{\rfloor }_{q\rightarrow p_2}\) and \(\bar{\mathbf {c}}_2={\lceil }{c_2}{\rfloor }_{q\rightarrow p_3})\).
-
Decryption: Given the secret key \(sk = \mathbf {s}\) and the ciphertext \(C=(\bar{\mathbf {c}}_1,\bar{\mathbf {c}}_2)\), compute \(z = {\lceil }{\bar{\mathbf {c}}_2}{\rfloor }_{p_3\rightarrow q} - \mathbf {s}^T{\lceil }{\bar{\mathbf {c}}_1}{\rfloor }_{p_2\rightarrow q}\) and output \( {\lceil }{z}{\rfloor }_{q\rightarrow 2} = {\lceil }{z\cdot \frac{2}{q}}{\rfloor } \bmod 2\) as the decryption result.
Similarly, for ciphertext \(C=(\bar{\mathbf {c}}_1,\bar{\mathbf {c}}_2)\) we have the same z and \(e'\) as defined in (2), where the difference is that now \({\Vert }{\mathbf {s}}{\Vert }_\infty \) and \({\Vert }{\mathbf {r}}{\Vert }_\infty \) are determined by \(\alpha _1\), and that \({\Vert }{\mathbf {e}}{\Vert }_\infty ,{\Vert }{\mathbf {x}_1}{\Vert }_\infty \) and \({|}{x_2}{|}\) are determined by \(\alpha _2\). Intuitively, we wish to use small \(\alpha _1\) in order to keep \({|}{e'}{|}\) small, and at the same time choose relatively large \(\alpha _2\) to remedy the potential security loss due to the choice of a small \(\alpha _1\).
While the intuition seems reasonable, it does not shed light on the choices of parameters, in particular, how parameters \(\alpha _1\) and \(\alpha _2\) (jointly) affect security. To this end, we consider the best known attacks and their variants against (A)LWE problems, and obtain the following conclusions: Let \(\chi _{\alpha _1}\) and \(\chi _{\alpha _2}\) be subgaussians with standard variances \(\alpha _1,\alpha _2\in \mathbb {R}\) respectively, then we have the following approximate relation between the hardness of ALWE and LWE: the hardness of ALWE with subgaussian standard variances \(\alpha _1,\alpha _2\in \mathbb {R}\) is polynomially equivalent to the hardness of LWE with subgaussian standard variance \(\sqrt{\alpha _1\alpha _2}\). Clearly, the equivalence is trivial for \(\alpha _1 = \alpha _2\). This confirms the feasibility of our idea: use a small \(\alpha _1\) to keep the probability \(\nu \) of decryption failures small while pick a relatively larger \(\alpha _2\) remain the security of the resulting PKE scheme.
The above idea can be naturally generalized to the schemes based on the ring and module versions of LWE. Actually, we will use AMLWE for achieving a better trade-off between computational and communication costs.
3.2 The Construction
We now formally describe a CCA-secure KEM from AMLWE (and AMLWE-R). For ease of implementation, we will use centered binomial distributions instead of Gaussian distributions as in [3, 6]. We first give an intermediate IND-CPA secure PKE, which is then transformed into an IND-CCA secure KEM by applying a tweaked Fujisaki-Okamoto (FO) transformation [14, 18].
An IND-CPA Secure PKE. Let \(n, q, k, \eta _1,\eta _2,\) \(d_t, d_u, d_v\) be positive integers. Let \(\mathcal {H}: \{0, 1\}^{n} \rightarrow R_q^{k\times k}\) be a hash function, which is modeled as a random oracle. The PKE scheme \({\varPi _\text {PKE}}\) consists of three algorithms \(({\mathsf {KeyGen}},\mathsf {Enc},\mathsf {Dec})\):
-
\({\varPi _\text {PKE}}.{\mathsf {KeyGen}}(\kappa )\): randomly choose \(\rho \xleftarrow {\$} \{0, 1\}^{n} \), \(\mathbf {s}\xleftarrow {\$}B_{\eta _1}^k,\mathbf {e}\xleftarrow {\$}B_{\eta _2}^k\), compute
 and
and 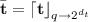 . Then, return the public key
. Then, return the public key  and the secret key \(sk = \mathbf {s}\).
and the secret key \(sk = \mathbf {s}\). -
\({\varPi _\text {PKE}}.\mathsf {Enc}(pk,\mu )\): given the public key
 and a plaintext \(\mu \in R_2\), randomly choose \(\mathbf {r}\xleftarrow {\$}B_{\eta _1}^k, \mathbf {e}_1\xleftarrow {\$}B_{\eta _2}^k, e_2 \xleftarrow {\$}B_{\eta _2}\), compute
and a plaintext \(\mu \in R_2\), randomly choose \(\mathbf {r}\xleftarrow {\$}B_{\eta _1}^k, \mathbf {e}_1\xleftarrow {\$}B_{\eta _2}^k, e_2 \xleftarrow {\$}B_{\eta _2}\), compute 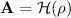 , \(\mathbf {u}= {\mathbf {A}}^T \mathbf {r}+ \mathbf {e}_1\),
, \(\mathbf {u}= {\mathbf {A}}^T \mathbf {r}+ \mathbf {e}_1\),  , and return the ciphertext
, and return the ciphertext 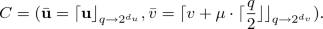
-
\({\varPi }_{{\text {PKE}}}.\mathsf {Dec}(sk,C)\): given the secret key \(sk = \mathbf {s}\) and a ciphertext \(C=(\bar{\mathbf {u}},\bar{v})\), compute \(z = {\lceil }{\bar{v}}{\rfloor }_{2^{d_v}\rightarrow q} - \mathbf {s}^T{\lceil }{\bar{\mathbf {u}}}{\rfloor }_{2^{d_u}\rightarrow q}\), output \( {\lceil }{z}{\rfloor }_{q\rightarrow 2} = {\lceil }{z\cdot \frac{2}{q}}{\rfloor } \bmod 2\).
Let \(\mathbf{c}_t \in R^k\) satisfy that

Let \(\mathbf{c}_u \in R^k\) satisfy that
Let \(c_v \in R\) satisfy that

Using the above equations, we have

It is easy to check that for any odd number q, we have that \(\mu ={\lceil }{z}{\rfloor }_{q\rightarrow 2}\) holds as long as  . In Sect. 3.4, we will choose the parameters such that the decryption algorithm succeeds with overwhelming probability.
. In Sect. 3.4, we will choose the parameters such that the decryption algorithm succeeds with overwhelming probability.
IND-CCA Secure KEM. Let \(\mathsf{G}: \{0, 1\}^{*} \rightarrow \{0, 1\}^{n} \), and \(\mathsf{H}: \{0, 1\}^{*} \rightarrow \{0, 1\}^{n} \times \{0, 1\}^{n} \) be two hash functions, which are modeled as random oracles. By applying a slightly tweaked Fujisaki-Okamoto (FO) transformation [14, 18], we can transform the above IND-CPA secure PKE \({\varPi }_{{\text {PKE}}}\) into an IND-CCA secure KEM (with implicit rejection) \({\varPi }_{\text {KEM}}=({\mathsf {KeyGen}},\mathsf {Encap},\mathsf {Decap})\) as follows.
-
\({\varPi }_{\text {KEM}}.{\mathsf {KeyGen}}(\kappa )\): choose \(z \xleftarrow {\$} \{0, 1\}^{n} \), compute
 . Then, return the public key \(pk =pk'\) and the secret key \(sk = (pk',sk',z)\).
. Then, return the public key \(pk =pk'\) and the secret key \(sk = (pk',sk',z)\). -
\({\varPi }_{\text {KEM}}.\mathsf {Encap}(pk)\): given the public key pk, randomly choose \(\mu \xleftarrow {\$} \{0, 1\}^{n} \), compute
 \(C = {\varPi }_{{\text {PKE}}}.\mathsf {Enc}(pk,\mu ';r)\) and \(K= \mathsf{H}(\bar{K}\Vert \mathsf{H}(C))\), where the notation \({\varPi }_{{\text {PKE}}}.\mathsf {Enc}(pk,\mu ';r)\) denotes running the algorithm \({\varPi }_{{\text {PKE}}}.\mathsf {Enc}(pk,\mu ')\) with fixed randomness r. Finally, return the ciphertext C and the encapsulated key K.
\(C = {\varPi }_{{\text {PKE}}}.\mathsf {Enc}(pk,\mu ';r)\) and \(K= \mathsf{H}(\bar{K}\Vert \mathsf{H}(C))\), where the notation \({\varPi }_{{\text {PKE}}}.\mathsf {Enc}(pk,\mu ';r)\) denotes running the algorithm \({\varPi }_{{\text {PKE}}}.\mathsf {Enc}(pk,\mu ')\) with fixed randomness r. Finally, return the ciphertext C and the encapsulated key K. -
\({\varPi }_{\text {KEM}}.\mathsf {Decap}(sk,C)\): given the secret key \(sk = (pk',sk',z)\) and a ciphertext C, compute
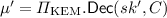 and \((\bar{K}', r') = \mathsf{G}(\mu '\Vert \mathsf{H}(pk')), C' = {\varPi }_{\text {KEM}}.\mathsf {Enc}(pk,\mu ';r')\). If \(C = C'\), return \(K=\mathsf{H}(\bar{K}' \Vert \mathsf{H}(C))\), else return \(\mathsf{H}(z \Vert \mathsf{H}(C))\).
and \((\bar{K}', r') = \mathsf{G}(\mu '\Vert \mathsf{H}(pk')), C' = {\varPi }_{\text {KEM}}.\mathsf {Enc}(pk,\mu ';r')\). If \(C = C'\), return \(K=\mathsf{H}(\bar{K}' \Vert \mathsf{H}(C))\), else return \(\mathsf{H}(z \Vert \mathsf{H}(C))\).
3.3 Provable Security
In the full version [32], we will show that under the hardness of the AMLWE problem and its rounding variant AMLWE-R (which is needed for compressing the public key, see Appendix A), our scheme \({\varPi }_{{\text {PKE}}}\) is provably IND-CPA secure. Formally, we have the following theorem.
Theorem 1
Let \(\mathcal {H}: \{0, 1\}^{n} \rightarrow R_q^{k\times k}\) be a random oracle. If both problems \(\mathrm {AMLWE}_{n,q,k,k,\eta _1,\eta _2}\) and  are hard, then the scheme \({\varPi }_{{\text {PKE}}}\) is IND-CPA secure.
are hard, then the scheme \({\varPi }_{{\text {PKE}}}\) is IND-CPA secure.
Since \({\varPi }_{\text {KEM}}\) is obtained by applying a slightly tweaked Fujisaki-Okamoto (FO) transformation [14, 18] to the PKE scheme \({\varPi }_{{\text {PKE}}}\), given the results in [6, 18] and Theorem 1, we have the following theorem.
Theorem 2
Under the AMLWE assumption and the AMLWE-R assumption, \({\varPi }_{\text {KEM}}\) is IND-CCA secure in the random oracle model.
Notice that the algorithm \(\mathsf {Decap}\) will always return a random “session key” even if the check fails (i.e., implicit rejection). Furthermore, the paper [20] showed that if the underlying PKE is IND-CPA secure, then the resulting KEM with implicit rejection obtained by using the FO transformation is also IND-CCA secure in the quantum random oracle model (QROM). Given the results in [20] and Theorem 1, we have the following theorem.
Theorem 3
Under the AMLWE assumption and the AMLWE-R assumption, \({\varPi }_{\text {KEM}}\) is IND-CCA secure in the QROM.
3.4 Choices of Parameters
In Table 5, we give three sets of parameters (namely, \({\varPi }_{\text {KEM}}\)-512, \({\varPi }_{\text {KEM}}\)-768 and \({\varPi }_{\text {KEM}}\)-1024) for \({\varPi }_{\text {KEM}}\), aiming at providing quantum security of at least 80, 128 and 192 bits, respectively. These parameters are carefully chosen such that the decryption failure probabilities (i.e., \(2^{-82}\), \(2^{-128}\) and \(2^{-211}\), respectively) are commensurate with the respective targeted security strengths. A concrete estimation of the security strength provided by the parameter sets will be given in Sect. 5. Among them, \({\varPi }_{\text {KEM}}\)-768 is the recommended parameter set. By the quantum searching algorithm [17], \(2\kappa \)-bit randomness/session key can only provide at most \(\kappa \) security. Even if the Grover algorithm cannot provide a quadratic speedup over classical algorithms in practice, we still set \({\varPi }_{\text {KEM}}\)-1024 to support an encryption of 64-bytes (512-bit) randomness/session key, aiming at providing a matching security strength, say, more than 210-bit estimated quantum security. Note that \({\varPi }_{\text {KEM}}\)-512 and \({\varPi }_{\text {KEM}}\)-768 only support an encryption of 32-byte (256-bit) session key.
We implemented our \({\varPi }_{\text {KEM}}\) on a 64-bit Ubuntu 14.4 LTS ThinkCenter desktop (equipped with Intel Core-i7 4790 3.6 GHz CPU and 4 GB memory). Particularly, the codes are mainly written using the C language, with partially optimized codes using AVX2 instructions to speedup some basic operations such as NTT operation and vector multiplications. The average number of CPU cycles (averaged over 10000 times) for running each algorithm is given in Table 1.
4 An Improved Signature from AMLWE and AMSIS
Our signature scheme is based on the “Fiat-Shamir with Aborts” technique [23], and bears most resemblance to Dilithium in [12]. The main difference is that our scheme uses the asymmetric MLWE and MSIS problems, which provides a flexible way to make a better trade-off between performance and security.
4.1 Design Rationale
Several lattice-based signature schemes were obtained by applying the Fiat-Shamir heuristic [13] to three-move identification schemes. For any positive integer n and q, let \(R = \mathbb {Z}[x]/(x^n+1)\) (resp., \(R_q = \mathbb {Z}_q[x]/(x^n+1)\)). Let \(\mathsf{H}: \{0, 1\}^{*} \rightarrow R_2\) be a hash function. Let \(k,\ell ,\eta \) be positive integers, and \(\gamma ,\beta >0\) be reals. We first consider an identification protocol between two users A and B based on the \(\mathrm {MSIS}^\infty _{n,q,k,\ell ,\beta }\) problem. Formally, user A owns a pair of public key  and secret key \(sk = \mathbf {x}\in R_q^\ell \). In order to convince another user B (who knows the public key pk) of his ownership of sk, A and B can execute the following protocol: (1) A first chooses a vector \(\mathbf {y}\in R^\ell \) from some distribution, and sends \(\mathbf {w}= {\mathbf {A}}\mathbf {y}\) to user B; (2) B randomly chooses a bit \(c\in R_q\), and sends it as a challenge to A; (3) A computes \(\mathbf {z}:= \mathbf {y}+ c\mathbf {x}\) and sends it back to B; B will accept the response \(\mathbf {z}\) by check if
and secret key \(sk = \mathbf {x}\in R_q^\ell \). In order to convince another user B (who knows the public key pk) of his ownership of sk, A and B can execute the following protocol: (1) A first chooses a vector \(\mathbf {y}\in R^\ell \) from some distribution, and sends \(\mathbf {w}= {\mathbf {A}}\mathbf {y}\) to user B; (2) B randomly chooses a bit \(c\in R_q\), and sends it as a challenge to A; (3) A computes \(\mathbf {z}:= \mathbf {y}+ c\mathbf {x}\) and sends it back to B; B will accept the response \(\mathbf {z}\) by check if  .
.
For the soundness (i.e., user A cannot cheat user B), B also has to make sure that \(\beta _2 = \Vert \mathbf {z}\Vert _\infty \) is sufficiently small (to ensure that the \(\mathrm {MSIS}^\infty _{n,q,k,\ell ,\beta }\) problem is hard), otherwise anyone can easily complete the proof by solving a linear equation. Moreover, we require that \(\beta _1 = \Vert \mathbf {x}\Vert _\infty \) is sufficiently small and \(\Vert \mathbf {y}\Vert _\infty \gg \Vert \mathbf {x}\Vert _\infty \) (and thus \(\beta _2 \gg \beta _1\)) holds to prevent user B from recovering the secret \(\mathbf {x}\) from the public key pk or the response \(\mathbf {z}\). Typically, we should require \(\beta _2/\beta _1 > 2^{\omega (\log \kappa )}\), where \(\kappa \) is the security parameter. This means that the identification protocol as well as its derived signature from the Fiat-Shamir heuristic will have a very large parameter size. To solve this problem, Lyubashevsky [23, 24] introduce the rejection sampling, which allows A to abort and restart the protocol (by choosing another \(\mathbf {y}\)) if he thinks \(\mathbf {z}\) might leak the information of \(\mathbf {x}\). This technique could greatly reduce the size of \(\mathbf {z}\) (since it allows to set \(\beta _2/\beta _1 = \mathsf {poly}(\kappa )\)), but the cost is painful for an interactive identification protocol. Fortunately, this technique will only increase the computation time of the signer when we transform the identification protocol into a signature scheme.
For any positive integer \(\eta \), \(S_\eta \) denotes the set of elements of R that each coefficient is taken from \(\{-\eta ,-\eta +1 \dots , \eta \}\). By the Fiat-Shamir heuristic, one can construct a signature scheme from the MSIS problem as follows:
-
Key generation: randomly choose \({\mathbf {A}}\xleftarrow {\$}R_q^{k \times \ell },\mathbf {x}\xleftarrow {\$}S_{\eta }^\ell \), and compute
 . Return the public key
. Return the public key 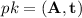 and secret key \(sk = (\mathbf {x},pk)\).
and secret key \(sk = (\mathbf {x},pk)\). -
Signing: given the secret key \(sk = (\mathbf {x},pk)\) and a message \(\mu \in \{0, 1\}^{*} \),
-
1.
randomly choose \(\mathbf {y}\xleftarrow {\$}S_{\gamma -1}^\ell \);
-
2.
compute \(\mathbf {w}= {\mathbf {A}}\mathbf {y}\) and \(c = \mathsf{H}(\mathbf {w}\Vert \mu )\);
-
3.
compute \(\mathbf {z}= \mathbf {y}+ c\mathbf {x}\);
-
4.
If \({\Vert }{\mathbf {z}}{\Vert }_\infty \ge \gamma - \beta \), restart the computation from step 1), where \(\beta \) is a bound such that \({\Vert }{c\mathbf {x}}{\Vert }_\infty \le \beta \) for all possible c and \(\mathbf {x}\). Otherwise, return the signature \(\sigma = (\mathbf {z},c)\).
-
1.
-
Verification: given the public key
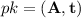 , a message \(\mu \in \{0, 1\}^{*} \) and a signature \(\sigma = (\mathbf {z},c)\), return 1 if \({\Vert }{\mathbf {z}}{\Vert }_\infty < \gamma - \beta \) and
, a message \(\mu \in \{0, 1\}^{*} \) and a signature \(\sigma = (\mathbf {z},c)\), return 1 if \({\Vert }{\mathbf {z}}{\Vert }_\infty < \gamma - \beta \) and 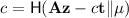 , and 0 otherwise.
, and 0 otherwise.
Informally, we require the \(\mathrm {MSIS}^\infty _{n,q,k,\ell ,\eta }\) problem to be hard for the security of the secret key (i.e., it is computationally infeasible to compute sk from pk). Moreover, we also require the \(\mathrm {MSIS}^\infty _{n,q,k,\ell ,2\gamma }\) problem to be hard for the unforgeability of signatures (i.e., it is computationally infeasible to forge a valid signature). Since \({\Vert }{c\mathbf {x}}{\Vert }_\infty \le \beta \), for any \((c,\mathbf {x})\) and \(\mathbf {z}\) output by the signing algorithm there always exists a \(\mathbf {y}\in S_{\gamma }^\ell \) such that \(\mathbf {z}= \mathbf {y}+ c\mathbf {x}\), which guarantees that the signature will not leak the information of the secret key. In terms of efficiency, the signing algorithm will repeat about \(\left( \frac{2(\gamma \, -\, \beta ) \, -\,1}{2\gamma \, -\,1}\right) ^{-n\cdot \ell }\) times to output a signature, and the signature size is about \(n\ell {\lceil }{\log _2(2(\gamma -\beta )-1)}{\rceil } + n\). Clearly, we wish to use a small \(\ell \) for better efficiency, but the hardness of the underlying MSIS problems require a relatively large \(\ell \).
To mediate the above conflict, one can use the MLWE problem, which can be seen as a special MSIS problem, to reduce the size of the key and signature. Formally, we can obtain the following improved signature scheme:
-
Key generation: randomly choose \({\mathbf {A}}\xleftarrow {\$}R_q^{k \times \ell }\), and \(\mathbf {s}_1\xleftarrow {\$}S_{\eta }^\ell ,\mathbf {s}_2\xleftarrow {\$}S_{\eta }^k\), compute
 . Return the public key
. Return the public key 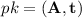 and secret key \(sk = (\mathbf {s}_1,\mathbf {s}_2,pk)\).
and secret key \(sk = (\mathbf {s}_1,\mathbf {s}_2,pk)\). -
Signing: given the secret key \(sk = (\mathbf {s}_1,\mathbf {s}_2,pk)\) and a message \(\mu \in \{0, 1\}^{*} \),
-
1.
randomly choose \(\mathbf {y}\xleftarrow {\$}S_{\gamma -1}^{\ell + k}\);
-
2.
compute \(\mathbf {w}= ({\mathbf {A}}\Vert \mathbf {I}_k)\mathbf {y}\) and \(c = \mathsf{H}(\mathbf {w}\Vert \mu )\);
-
3.
compute \(\mathbf {z}= \mathbf {y}+ c\left( \begin{array}{c}\mathbf {s}_1 \\ \mathbf {s}_2\end{array}\right) \);
-
4.
If \({\Vert }{\mathbf {z}}{\Vert }_\infty \ge \gamma - \beta \), restart the computation from step (1), where \(\beta \) is a bound such that \(\left\| c\left( \begin{array}{c}\mathbf {s}_1 \\ \mathbf {s}_2\end{array}\right) \right\| _\infty \le \beta \) holds for all possible \(c,\mathbf {s}_1,\mathbf {s}_2\). Otherwise, output the signature \(\sigma = (\mathbf {z},c)\).
-
1.
-
Verification: given the public key
 , a message \(\mu \in \{0, 1\}^{*} \) and a signature \(\sigma = (\mathbf {z},c)\), return 1 if \({\Vert }{\mathbf {z}}{\Vert }_\infty < \gamma - \beta \) and
, a message \(\mu \in \{0, 1\}^{*} \) and a signature \(\sigma = (\mathbf {z},c)\), return 1 if \({\Vert }{\mathbf {z}}{\Vert }_\infty < \gamma - \beta \) and  , otherwise return 0.
, otherwise return 0.
Furthermore, since \(\mathbf {w}= ({\mathbf {A}}\Vert \mathbf {I}_k)\mathbf {y}= {\mathbf {A}}\mathbf {y}_1 + \mathbf {y}_2\) where \(\mathbf {y}=(\mathbf {y}_1^T,\mathbf {y}_2^T)\) and  , we have that the higher bits of (each coefficient of) \(\mathbf {w}\) is almost determined by high order bits of (the corresponding coefficient of) \({\mathbf {A}}\mathbf {y}_1\). This fact has been utilized by [5, 12] to compress the signature size. Formally, denote \(\mathsf {HighBits}(\mathbf {z},2\gamma _2)\) and \(\mathsf {LowBits}(\mathbf {z},2\gamma _2)\) be polynomial vector defined by the high order bits and low order bits of a polynomial vector \(\mathbf {z}\in R_q^k\) related to a parameter \(\gamma _2\). We can obtain the following signature scheme:
, we have that the higher bits of (each coefficient of) \(\mathbf {w}\) is almost determined by high order bits of (the corresponding coefficient of) \({\mathbf {A}}\mathbf {y}_1\). This fact has been utilized by [5, 12] to compress the signature size. Formally, denote \(\mathsf {HighBits}(\mathbf {z},2\gamma _2)\) and \(\mathsf {LowBits}(\mathbf {z},2\gamma _2)\) be polynomial vector defined by the high order bits and low order bits of a polynomial vector \(\mathbf {z}\in R_q^k\) related to a parameter \(\gamma _2\). We can obtain the following signature scheme:
-
Key generation: randomly choose \({\mathbf {A}}\xleftarrow {\$}R_q^{k \times \ell }\), and \(\mathbf {s}_1\xleftarrow {\$}S_{\eta }^\ell ,\mathbf {s}_2\xleftarrow {\$}S_{\eta }^k\), compute
 . Return the public key
. Return the public key  and secret key \(sk = (\mathbf {s}_1,\mathbf {s}_2,pk)\).
and secret key \(sk = (\mathbf {s}_1,\mathbf {s}_2,pk)\). -
Signing: given the secret key \(sk = (\mathbf {s}_1,\mathbf {s}_2,pk)\) and a message \(\mu \in \{0, 1\}^{*} \),
-
1.
randomly choose \(\mathbf {y}\xleftarrow {\$}S_{\gamma _1 -1}^{\ell }\);
-
2.
compute \(\mathbf {w}= {\mathbf {A}}\mathbf {y}\) and \(c = \mathsf{H}(\mathsf {HighBits}(\mathbf {w},2\gamma _2)\Vert \mu )\);
-
3.
compute \(\mathbf {z}= \mathbf {y}+ c\mathbf {s}_1\);
-
4.
If \({\Vert }{\mathbf {z}}{\Vert }_\infty \ge \gamma _1 - \beta \) or \(\mathsf {LowBits}({\mathbf {A}}\mathbf {y}- c\mathbf {s}_2,2\gamma _2)\ge \gamma _2 - \beta \), restart the computation from step 1), where \(\beta \) is a bound such that \({\Vert }{c\mathbf {s}_1}{\Vert }_\infty ,{\Vert }{c\mathbf {s}_2}{\Vert }_\infty \le \beta \) hold for all possible \(c,\mathbf {s}_1,\mathbf {s}_2\). Otherwise, output the signature \(\sigma = (\mathbf {z},c)\).
-
1.
-
Verification: given the public key
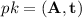 , a message \(\mu \in \{0, 1\}^{*} \) and a signature \(\sigma = (\mathbf {z},c)\), return 1 if \({\Vert }{\mathbf {z}}{\Vert }_\infty < \gamma _1 - \beta \) and
, a message \(\mu \in \{0, 1\}^{*} \) and a signature \(\sigma = (\mathbf {z},c)\), return 1 if \({\Vert }{\mathbf {z}}{\Vert }_\infty < \gamma _1 - \beta \) and 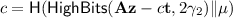 , otherwise return 0.
, otherwise return 0.
Essentially, the checks in step (4) are used to ensure that (1) the signature \((\mathbf {z},c)\) will not leak the information of \(\mathbf {s}_1\) and \(\mathbf {s}_2\); and (2)  (note that \(\mathbf {w}= {\mathbf {A}}\mathbf {y}= {\mathbf {A}}\mathbf {y}\,-\,c\mathbf {s}_2 + c\mathbf {s}_2\), \(\mathsf {LowBits}({\mathbf {A}}\mathbf {y}\,-\, c\mathbf {s}_2,2\gamma _2)< \gamma _2 \,-\, \beta \) and \({\Vert }{c\mathbf {s}_2}{\Vert }_\infty \le \beta \)). By setting \(\gamma _1 = 2\gamma _2\), we require the \(\mathrm {MLWE}_{n,k,\ell ,q,\eta }\) problem and the (variant of) \(\mathrm {MSIS}^\infty _{n,k,(\ell + k+1),q,2\gamma _1+2}\) problem to be hard to ensure the security of the secret key and the unforgeability of the signature, respectively.
(note that \(\mathbf {w}= {\mathbf {A}}\mathbf {y}= {\mathbf {A}}\mathbf {y}\,-\,c\mathbf {s}_2 + c\mathbf {s}_2\), \(\mathsf {LowBits}({\mathbf {A}}\mathbf {y}\,-\, c\mathbf {s}_2,2\gamma _2)< \gamma _2 \,-\, \beta \) and \({\Vert }{c\mathbf {s}_2}{\Vert }_\infty \le \beta \)). By setting \(\gamma _1 = 2\gamma _2\), we require the \(\mathrm {MLWE}_{n,k,\ell ,q,\eta }\) problem and the (variant of) \(\mathrm {MSIS}^\infty _{n,k,(\ell + k+1),q,2\gamma _1+2}\) problem to be hard to ensure the security of the secret key and the unforgeability of the signature, respectively.
By a careful examination on the above scheme, one can find that the computational efficiency of the signing algorithm is determined by the expected number of repetitions in step (4):
where \(N_1\) and \(N_2\) are determined by the first and second checks in step (4), respectively. Clearly, it is possible to modify \(N_1\) and \(N_2\) while keeping the total number of repetitions \(N = N_1\cdot N_2\) unchanged. Note that the size of the signature is related to \(\gamma _1\) and is irrelevant to \(\gamma _2\), which means that a shorter signature can be obtained by using a smaller \(\gamma _1\). However, simply using a smaller \(\gamma _1\) will also give a bigger \(N_1\), and thus a worse computational efficiency. In order to obtain a short signature size without (significantly) affecting the computational efficiency:
-
We use the AMLWE problem for the security of the secret key, which allows us to use a smaller \(\gamma _1\) by reducing \({\Vert }{\mathbf {s}_1}{\Vert }_\infty \) (and thus \(\beta = {\Vert }{c\mathbf {s}_1}{\Vert }_\infty \) in the expression of \(N_1\));
-
We use the AMSIS problem for the unforgeability of the signatures, which further allows us to use a smaller \(\gamma _1\) by increasing \(\gamma _2\) to keep \(N = N_1 \cdot N_2\) unchanged.
Note that reducing \({\Vert }{\mathbf {s}_1}{\Vert }_\infty \) (by choosing a smaller \(\eta _1\)) may weaken the hardness of the underlying AMLWE problem (if we do not change other parameters). We choose to increase \(\eta _2\) (and thus \({\Vert }{\mathbf {s}_2}{\Vert }_\infty \)) to remain the hardness. Similarly, increasing \(\gamma _2\) will weaken the hardness of the underlying AMSIS problem, and we choose to reduce \(\gamma _1\) to remain the hardness. Both strategies crucially rely on the asymmetries of the underlying problems.
4.2 The Construction
Let \(n,k,\ell ,q,\eta _1,\eta _2,\beta _1,\beta _2,\gamma _1,\gamma _2,\omega \in \mathbb {Z}\) be positive integers. Let \(R = \mathbb {Z}[x]/(x^n+1)\) and \(R_q = \mathbb {Z}_q[x]/(x^n+1)\). Denote \(B_{60}\) as the set of elements of R that have 60 coefficients are either \(-1\) or 1 and the rest are 0, and \(|B_{60}|=2^{60}\cdot {n \atopwithdelims ()60}\). When \(n=256\), \(|B_{60}|>2^{256}\). Let \(\mathsf{H}_1: \{0, 1\}^{256} \rightarrow R_q^{k\times \ell }, \mathsf{H}_2: \{0, 1\}^{*} \rightarrow \{0, 1\}^{384} , \) \(\mathsf{H}_3: \{0, 1\}^{*} \rightarrow S_{\gamma _1-1}^\ell \) and \(\mathsf{H}_4: \{0, 1\}^{*} \rightarrow B_{60}\) be four hash functions. We now present the description of our scheme \({\varPi }_{{\text {SIG}}}=(\mathsf {KeyGen},\) \(\mathsf {Sign},\mathsf {Verify})\):
-
\({\varPi }_{{\text {SIG}}}.\mathsf {KeyGen}(\kappa )\): first randomly choose \(\rho ,K \xleftarrow {\$}\{0,1\}^{256},\) \(\mathbf {s}_1 \xleftarrow {\$}S_{\eta _1}^\ell , \mathbf {s}_2\xleftarrow {\$}S_{\eta _2}^k\). Then, compute
 and \({ tr}=\mathsf{H}_2(\rho \Vert \mathbf{t}_1)\in \{0,1\}^{384}\). Finally, return the public key
and \({ tr}=\mathsf{H}_2(\rho \Vert \mathbf{t}_1)\in \{0,1\}^{384}\). Finally, return the public key  and secret key \(sk=(\rho ,K, { tr}, \mathbf{s}_1, \mathbf{s}_2, \mathbf{t}_0)\).
and secret key \(sk=(\rho ,K, { tr}, \mathbf{s}_1, \mathbf{s}_2, \mathbf{t}_0)\). -
\({\varPi }_{{\text {SIG}}}.\mathsf {Sign}(sk, M)\): given \(sk=(\rho , K, { tr}, \mathbf{s}_1, \) \(\mathbf{s}_2, \mathbf{t}_0)\) and a message \(M\in \{0,1\}^*\), first compute \(\mathbf{A}=\mathsf{H}_1(\rho )\in R_q^{k\times \ell }\), \(\mu =\mathsf{H}_2({ tr} \Vert M)\in \{0,1\}^{384}\), and set \(ctr=0\). Then, perform the following computations:
-
1.
\(\mathbf{y}=\mathsf{H}_3(K\Vert \mu \Vert ctr)\in S_{\gamma _1-1}^\ell \) and \(\mathbf{w}=\mathbf{A}{} \mathbf{y}\);
-
2.
\(\mathbf{w}_1=\mathsf{HighBits}_q(\mathbf{w}, 2\gamma _2)\) and \(c=\mathsf{H}_4(\mu \Vert \mathbf{w}_1)\in B_{60}\);
-
3.
\(\mathbf{z}=\mathbf{y}+c\mathbf{s}_1\) and \(\mathbf{u}=\mathbf{w}-c\mathbf{s}_2\);
-
4.
\((\mathbf{r}_1, \mathbf{r}_0)=\mathsf{Decompose}_q(\mathbf{u}, 2\gamma _2)\);
-
5.
if
 or
or  or \(\mathbf{r}_1 \ne \mathbf{w}_1\), then set \(ctr=ctr+1\) and restart the computation from step (1);
or \(\mathbf{r}_1 \ne \mathbf{w}_1\), then set \(ctr=ctr+1\) and restart the computation from step (1); -
6.
compute \(\mathbf{v} = c \mathbf{t}_0\) and \(\mathbf{h} = \mathsf{MakeHint}_q(-\mathbf{v}, \mathbf{u}+\mathbf{v}, 2\gamma _2)\);
-
7.
if
 or the number of 1’s in \(\mathbf{h}\) is greater than \(\omega \), then set \(ctr=ctr+1\) and restart the computation from step 1);
or the number of 1’s in \(\mathbf{h}\) is greater than \(\omega \), then set \(ctr=ctr+1\) and restart the computation from step 1); -
8.
return the signature \(\sigma = (\mathbf{z},\mathbf{h},c)\).
-
1.
-
\({\varPi }_{{\text {SIG}}}.\mathsf {Verify}(pk, M, \sigma )\): given the public key \(pk=(\rho , \mathbf{t}_1)\), a message \(M\in \{0,1\}^*\) and a signature \(\sigma = (\mathbf{z},\mathbf{h},c)\), first compute \(\mathbf{A}=\mathsf{H}_1(\rho )\in R_q^{k\times \ell }, \mu =\mathsf{H}_2(\mathsf{H}_2(pk) \Vert M)\in \{0,1\}^{384}\). Let \(\mathbf{u}=\mathbf{A}{} \mathbf{z}-c\mathbf{t}_1\cdot 2^d, \mathbf{w}_1'=\mathsf{UseHints}_q(\mathbf{h}, \mathbf{u}, 2\gamma _2)\) and \(c'=\mathsf{H}_4(\mu \Vert \mathbf{w}_1')\). Finally, return 1 if
 and the number of 1’s in \(\mathbf{h}\) is \(\le \omega \), otherwise return 0.
and the number of 1’s in \(\mathbf{h}\) is \(\le \omega \), otherwise return 0.
We note that the hash function \(\mathsf{H}_3\) is basically used to make the signing algorithm \(\mathsf {Sign}\) deterministic, which is needed for a (slightly) tighter security proof in the quantum random oracle model. One can remove \(\mathsf{H}_3\) by directly choosing \(\mathbf {y}\xleftarrow {\$}S_{\gamma _1-1}^\ell \) at random, and obtain a probabilistic signing algorithm. We also note that the hash function \(\mathsf{H}_4\) can be constructed by using an extendable output function such as SHAKE-256 [29] and a so-called “inside-out” version of Fisher-Yates shuffle algorithm [21]. The detailed constructions of hash functions \(\mathsf{H}_3\) and \(\mathsf{H}_4\) can be found in [12].
Correctness. Note that if  , by Lemma 1 we have \(\mathsf{UseHint}_q(\mathbf{h}, \mathbf{w}-c\mathbf{s}_2+c\mathbf{t}_0, 2\gamma _2)=\mathsf{HighBits}_q(\mathbf{w}-c\mathbf{s}_2, 2\gamma _2)\). Since \(\mathbf{w}=\mathbf{Ay}\) and \(\mathbf{t}=\mathbf{A}{} \mathbf{s}_1+\mathbf{s}_2\), we have that
, by Lemma 1 we have \(\mathsf{UseHint}_q(\mathbf{h}, \mathbf{w}-c\mathbf{s}_2+c\mathbf{t}_0, 2\gamma _2)=\mathsf{HighBits}_q(\mathbf{w}-c\mathbf{s}_2, 2\gamma _2)\). Since \(\mathbf{w}=\mathbf{Ay}\) and \(\mathbf{t}=\mathbf{A}{} \mathbf{s}_1+\mathbf{s}_2\), we have that
where  . Therefore, the verification algorithm computes
. Therefore, the verification algorithm computes
As the signing algorithm checks that \(\mathbf{r}_1=\mathbf{w}_1\), this is equivalent to
Hence, the \(\mathbf{w}_1\) computed by the verification algorithm is the same as that of the signing algorithm, and thus the verification algorithm will always return 1.
Number of Repetitions. Since our signature scheme uses the rejection sampling [23, 24] to generate \((\mathbf{z}, \mathbf{h})\), the efficiency of the signing algorithm is determined by the number of repetitions that will be caused by steps (5) and (7) of the signing algorithm. We first estimate the probability that  holds in step (5). Assuming that \({\Vert }{c\mathbf {s}_1}{\Vert }_\infty \le \beta _1\) holds, then we always have \({\Vert }{\mathbf {z}}{\Vert }_\infty \le \gamma _1 -\beta _1-1\) whenever \({\Vert }{\mathbf {y}}{\Vert }_\infty \le \gamma _1-2\beta _1-1\). The size of this range is \(2(\gamma _1-\beta _1)-1\). Note that each coefficient of \(\mathbf {y}\) is chosen randomly from \(2\gamma _1-1\) possible values. That is, for a fixed \(c\mathbf {s}_1\), each coefficient of vector \(\mathbf {z}=\mathbf {y}+ c\mathbf {s}_1\) has \(2\gamma _1-1\) possibilities. Therefore, the probability that \({\Vert }{\mathbf {z}}{\Vert }_\infty \le \gamma _1 -\beta _1-1\) is
holds in step (5). Assuming that \({\Vert }{c\mathbf {s}_1}{\Vert }_\infty \le \beta _1\) holds, then we always have \({\Vert }{\mathbf {z}}{\Vert }_\infty \le \gamma _1 -\beta _1-1\) whenever \({\Vert }{\mathbf {y}}{\Vert }_\infty \le \gamma _1-2\beta _1-1\). The size of this range is \(2(\gamma _1-\beta _1)-1\). Note that each coefficient of \(\mathbf {y}\) is chosen randomly from \(2\gamma _1-1\) possible values. That is, for a fixed \(c\mathbf {s}_1\), each coefficient of vector \(\mathbf {z}=\mathbf {y}+ c\mathbf {s}_1\) has \(2\gamma _1-1\) possibilities. Therefore, the probability that \({\Vert }{\mathbf {z}}{\Vert }_\infty \le \gamma _1 -\beta _1-1\) is
Now, we estimate the probability that

holds in step (5). If we (heuristically) assume that each coefficient of \(\mathbf {r}_0\) is uniformly distributed modulo \(2\gamma _2\), the probability that \({\Vert }{\mathbf {r}_0}{\Vert }_{\infty }<\gamma _2-\beta _2\) is
By Lemma 2, if  , then
, then  implies that \(\mathbf{r}_1=\mathbf{w}_1\). This means that the overall probability that step (5) will not cause a repetition is
implies that \(\mathbf{r}_1=\mathbf{w}_1\). This means that the overall probability that step (5) will not cause a repetition is
Finally, under our choice of parameters, the probability that step (7) of the signing algorithm will cause a repetition is less than 1%. Thus, the expected number of repetitions is roughly \(e^{n(\ell \beta _1/\gamma _1+k \beta _2/\gamma _2)}\).
4.3 Provable Security
In the full version [32], we show that under the hardness of the AMLWE problem and a rounding variant AMSIS-R of AMSIS (which is needed for compressing the public key, see Appendix A), our scheme \({\varPi }_{{\text {SIG}}}\) is provably SUF-CMA secure in the ROM. Formally, we have the following theorem.
Theorem 4
If \(\mathsf{H}_1: \{0, 1\}^{256} \rightarrow R_q^{k\times \ell }\) and \(\mathsf{H}_4: \{0, 1\}^{*} \rightarrow B_{60}\) are random oracles, the outputs of \(\mathsf{H}_3: \{0, 1\}^{*} \rightarrow S_{\gamma _1-1}^\ell \) are pseudo-random, and \(\mathsf{H}_2: \{0, 1\}^{*} \rightarrow \{0, 1\}^{384} \) is a collision-resistant hash function, then \(\varPi _{\text {SIG}}\) is SUF-CMA secure under the \(\mathrm {AMLWE}_{n,q,k,\ell ,\eta _1,\eta _2}\) and \(\mathrm {AMSIS\text{- }R}^{\infty }_{n,q,d,k,\ell ,4\gamma _2+2,2\gamma _1}\) assumptions.
Furthermore, under an interactive variant SelfTargetAMSIS of the AMSIS problem (which is an asymmetric analogue of the SelfTargetMSIS problem introduced by Ducas et al. [12]), we can also prove that our scheme \({\varPi }_{{\text {SIG}}}\) is provably SUF-CMA secure. Formally, we have that following theorem.
Theorem 5
In the quantum random oracle model (QROM), signature scheme \(\varPi _{\mathrm {SIG}}\) is SUF-CMA secure under the following assumptions: \(\mathrm {AMLWE}_{n,q,k,\ell ,\eta _1,\eta _2}\), \(\mathrm {AMSIS}^\infty _{n,q,d,k,\ell ,4\gamma _2+2,2(\gamma _1-\beta _1)}\) and \(\mathrm {SelfTargetAMSIS}^\infty _{\mathsf{H}_4,n,q,k,\ell _1,\ell _2, 4\gamma _2,(\gamma _1-\beta _1)}\).
4.4 Choices of Parameters
In Table 6, we provide three sets of parameters (i.e., \({\varPi }_{{\text {SIG}}}\)-1024, \({\varPi }_{{\text {SIG}}}\)-1280 and \({\varPi }_{{\text {SIG}}}\)-1536) for our signature scheme \(\varPi _{\text {SIG}}\), which provide 80-bit, 128-bit and 160-bit quantum security, respectively (corresponding to 98-bit, 141-bit and 178-bit classical security, respectively). A concrete estimation of the security provided by the parameter sets will be given in Sect. 5. Among them, \({\varPi }_{{\text {SIG}}}\)-1280 is the recommended parameter set.
Our scheme \(\varPi _{\text {SIG}}\) under the same machine configuration as in Sect. 3.4 is implemented using standard C, where some partial optimization techniques (e.g., AVX2 instructions) are adopted to speedup basic operations such as NTT operation. The average CPU cycles (averaged over 10000 times) needed for running the algorithms are given in Table 3.
5 Known Attacks Against AMLWE and AMSIS
Solvers for LWE mainly include primal attacks, dual attacks (against the underlying lattice problems) and direct solving algorithms such as BKW and Arora-Ge [2]. BKW and Arora-Ge attacks need sub-exponentially (or even exponentially) many samples, and thus they are not relevant to the public-key cryptography scenario where only a restricted amount of samples is available. Therefore, for analyzing and evaluating practical lattice-based cryptosystems, we typically consider only primal attacks and dual attacks. Further, these two attacks, which are the currently most relevant and effective, seem not to have additional advantages in solving RLWE/MLWE over standard LWE. Thus, when analyzing RLWE or MLWE based cryptosystems, one often translates RLWE/MLWE instances to the corresponding LWE counterparts [6, 12] and then applies the attacks. In particular, one first transforms \(\mathrm {AMLWE}_{n,q,k,\ell , \alpha _1,\alpha _2}\) into \(\mathrm {ALWE}_{nk,q,k\ell , \alpha _1,\alpha _2}\), and then applies, generalizes and optimizes the LWE solving algorithms to ALWE. Since any bounded centrally symmetric distribution can be regarded as subgaussian for a certain parameter, for simplicity and without loss of generality, we consider the case that secret vector and error vector in \(\mathrm {ALWE}_{n,q,m,\alpha _1,\alpha _2}\) are sampled from subgaussians with parameters \(\alpha _1\) and \(\alpha _2\) respectively. Formally, the problem is to recover \(\mathbf {s}\) from samples
where \({\mathbf {A}}\xleftarrow {\$}\mathbb {Z}_q^{m\times n}\), \(\mathbf {s}\leftarrow \chi _{\alpha _1}^n\) and \(\mathbf {e}\leftarrow \chi _{\alpha _2}^m\).
In the full version [32], we will not only consider the traditional primal attack and dual attack against ALWE, but also consider two variants of primal attack and three variants of dual attack, which are more efficient to solve the ALWE problem by taking into account the asymmetry of ALWE.
As for the best known attacks against (A)SIS, the BKZ lattice basis reduction algorithm and its variants are more useful for solving the \(\ell _2\)-norm (A)SIS problem than the \(\ell _\infty \)-norm counterpart. Note that a solution \(\mathbf {x}=(\mathbf {x}_1^T,\mathbf {x}_2^T)^T\in \mathbb {Z}^{m_1 + m_2}\) to the infinity-norm ASIS instance \({\mathbf {A}}\in \mathbb {Z}_q^{n\times (m_1 + m_2 - n)}\), where \((\mathbf {I}_n\Vert {\mathbf {A}})\mathbf {x}= \mathbf {0}\bmod q\) and \({\Vert }{\mathbf {x}}{\Vert }_\infty \le \max (\beta _1,\beta _2)< q\), may have \({\Vert }{\mathbf {x}}{\Vert } > q\), whose \(\ell _2\)-norm is even larger than that of a trivial solution \(\mathbf {u}= (q,0,\dots ,0)^T\). We will follow [12] to solve the \(\ell _\infty \)-norm SIS problem. Further, we can always apply an \(\ell _2\)-norm SIS solve to the \(\ell _\infty \)-norm SIS problem due to the relation \( {\Vert }{\mathbf {x}}{\Vert }_\infty \le {\Vert }{\mathbf {x}}{\Vert }\). Hereafter we refer to the above two algorithms as \(\ell _\infty \)-norm and \(\ell _2\)-norm attacks respectively, and use them to estimate the concrete complexity of solving \(\mathrm {ASIS}^\infty _{n,q,m_1,m_2,\beta _1,\beta _2}\). As before, when analyzing RSIS or MSIS based cryptosystems, one often translates RSIS/MSIS instances to the corresponding SIS counterparts [12] and then applies the attacks.
In the full version [32], we will not only consider the traditional \(\ell _2\) norm attack and \(\ell _\infty \) norm attack against ASIS, but also consider one variant of \(\ell _2\) norm attack and two variants of \(\ell _\infty \) norm attack, which are more efficient to solve the ASIS problem by taking into consideration the asymmetry of ASIS.
In the following two subsections, we will summarize those attacks against our \({\varPi }_{\text {KEM}}\) and \({\varPi }_{{\text {SIG}}}\) schemes.
5.1 Concrete Security of \({\varPi }_{\text {KEM}}\)
The complexity varies for the type of attacks, the number m of samples used and choice of \(b\in \mathbb {Z}\) to run the BKZ\(\text{- }b\) algorithm. Therefore, in order to obtain an overall security estimation sec of the \({\varPi }_{\text {KEM}}\) under the three proposed parameter settings, we enumerate all possible values of m (the number of ALWE samples) and b to reach a conservative estimation about the computational complexity of primal attacks and dual attacks, by using a python script (which is planned to be uploaded together with the implementation of our schemes to a public repository later). Tables 7 and 8 estimate the complexities of the three parameter sets against primal attacks and dual attacks by taking the minimum of sec over all possible values of (m, b). Taking into account the above, Table 9 shows the overall security of \({\varPi }_{\text {KEM}}\).
Further, in order to study the complexity relations of asymmetric (M)LWE and standard (M)LWE, we give a comparison in Table 10 between the AMLWE and the corresponding MLWE, in terms of the parameter choices used by \({\varPi }_{\text {KEM}}\), which shows that the hardness of AMLWE with Gaussian standard variances \(\alpha _1,\alpha _2\) is “comparable” to that of MLWE with Gaussian standard variance \(\sqrt{\alpha _1\alpha _2}\). We note that the comparison only focuses on security, and the corresponding MLWE, for the parameters given in Table 10, if ever used to build a KEM, cannot achieve the same efficiency and correctness as our \({\varPi }_{\text {KEM}}\) does.
5.2 Concrete Security of \({\varPi }_{{\text {SIG}}}\)
As before, in order to obtain an overall security estimation of the \({\varPi }_{{\text {SIG}}}\) under the three proposed parameter settings against key recovery attacks, we enumerate all possible values of m and b to reach a conservative estimation sec about the computational complexities of primal attacks and dual attacks by using a python script. Tables 11 and 12 estimate the complexities of the three parameter sets of the underlying ALWE problem against primal attacks and dual attacks by taking the minimum of sec over all possible values of (m, b).
Likewise, we enumerate all possible values of m and b to reach a conservative estimation sec about the computational complexities of \(\ell _2\)-norm and \(\ell _\infty \)-norm attacks. Tables 13 and 14 estimate the complexities of the three parameter sets of the underlying ASIS problem against \(\ell _2\)-normal and \(\ell _\infty \)-normal attacks by taking the minimum of sec over all possible values of (m, b).
In Table 15, we give the overall security of \({\varPi }_{{\text {SIG}}}\) under the three parameter settings against key recovery and forgery attacks, which takes account of both AMLWE and AMSIS attacks.
Notes
- 1.
In the full version, we show that the relations actually hold for discrete Gaussian distributions and binomial distributions under certain choices of parameters.
References
Ajtai, M.: Generating hard instances of lattice problems (extended abstract). In: Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, STOC 1996, pp. 99–108. ACM, New York, NY, USA (1996)
Albrecht, M.R., Player, R., Scott, S.: On the concrete hardness of learning with errors. J. Math. Cryptol. 9, 169–203 (2015)
Alkim, E., Ducas, L., Pöppelmann, T., Schwabe, P.: Post-quantum key exchange-a new hope. In: USENIX Security Symposium 2016 (2016)
Applebaum, B., Cash, D., Peikert, C., Sahai, A.: Fast cryptographic primitives and circular-secure encryption based on hard learning problems. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 595–618. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_35
Bai, S., Galbraith, S.D.: An improved compression technique for signatures based on learning with errors. In: Benaloh, J. (ed.) CT-RSA 2014. LNCS, vol. 8366, pp. 28–47. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04852-9_2
Bos, J., et al.: CRYSTALS - Kyber: a CCA-secure module-lattice-based KEM. In: 2018 IEEE European Symposium on Security and Privacy (EuroS P), pp. 353–367, April 2018
Brakerski, Z., Gentry, C., Vaikuntanathan, V.: Fully homomorphic encryption without bootstrapping. In: Innovations in Theoretical Computer Science, ITCS, pp. 309–325 (2012)
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. In: 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science (FOCS), pp. 97–106, October 2011
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: Classical hardness of learning with errors. In: Proceedings of the Forty-fifth Annual ACM Symposium on Theory of Computing, STOC 2013, pp. 575–584. ACM, New York, NY, USA (2013)
Brakerski, Z., Vaikuntanathan, V.: Fully homomorphic encryption from ring-LWE and security for key dependent messages. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 505–524. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_29
Cheon, J.H., Kim, D., Lee, J., Song, Y.: Lizard: cut off the tail! A practical post-quantum public-key encryption from LWE and LWR. In: Catalano, D., De Prisco, R. (eds.) SCN 2018. LNCS, vol. 11035, pp. 160–177. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98113-0_9
Ducas, L., et al.: Crystals-dilithium: a lattice-based digital signature scheme. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2018(1), 238–268 (2018)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. J. Cryptol. 26(1), 80–101 (2013)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Proceedings of the 40th Annual ACM Symposium on Theory of Computing, STOC 2008, pp. 197–206. ACM, New York, NY, USA (2008)
Goldwasser, S., Kalai, Y., Peikert, C., Vaikuntanathan, V.: Robustness of the learning with errors assumption. In: Proceedings of the Innovations in Computer Science 2010. Tsinghua University Press (2010)
Grover, L.K.: A fast quantum mechanical algorithm for database search. In: STOC 1996, pp. 212–219. ACM (1996)
Hofheinz, D., Hövelmanns, K., Kiltz, E.: A modular analysis of the Fujisaki-Okamoto transformation. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 341–371. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_12
IBM: IBM unveils world’s first integrated quantum computing system for commercial use (2019). https://newsroom.ibm.com/2019-01-08-IBM-Unveils-Worlds-First-Integrated-Quantum-Computing-System-for-Commercial-Use
Jiang, H., Zhang, Z., Chen, L., Wang, H., Ma, Z.: IND-CCA-secure key encapsulation mechanism in the quantum random oracle model, revisited. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 96–125. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_4
Knuth, D.: The Art of Computer Programming, vol. 2, 3rd edn. Addison-Wesley, Boston (1997)
Lindner, R., Peikert, C.: Better key sizes (and Attacks) for LWE-based encryption. In: Kiayias, A. (ed.) CT-RSA 2011. LNCS, vol. 6558, pp. 319–339. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19074-2_21
Lyubashevsky, V.: Fiat-Shamir with aborts: applications to lattice and factoring-based signatures. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 598–616. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_35
Lyubashevsky, V.: Lattice signatures without trapdoors. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 738–755. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_43
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_1
Micciancio, D.: On the hardness of learning with errors with binary secrets. Theory Comput. 14(13), 1–17 (2018)
Micciancio, D., Regev, O.: Worst-case to average-case reductions based on gaussian measures. In: Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science 2004, pp. 372–381 (2004)
NSA National Security Agency. Cryptography today, August 2015. https://www.nsa.gov/ia/programs/suiteb_cryptography/
National Institute of Standards and Technology. SHA-3 standard: permutation-based hash and extendable-output functions. FIPS PUB 202 (2015). http://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.202.pdf
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Proceedings of the Thirty-Seventh Annual ACM Symposium on Theory of Computing, STOC 2005, pp. 84–93. ACM, New York, NY, USA (2005)
Shor, P.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26(5), 1484–1509 (1997)
Zhang, J., Yu, Y., Fan, S., Zhang, Z., Yang, K.: Tweaking the asymmetry of asymmetric-key cryptography on lattices: KEMs and signatures of smaller sizes. Cryptology ePrint Archive, Report 2019/510 (2019)
Acknowledgments
We thank the anonymous reviewers for their helpful suggestions. Jiang Zhang is supported by the National Natural Science Foundation of China (Grant Nos. 61602046, 61932019), the National Key Research and Development Program of China (Grant Nos. 2017YFB0802005, 2018YFB0804105), the Young Elite Scientists Sponsorship Program by CAST (2016QNRC001), and the Opening Project of Guangdong Provincial Key Laboratory of Data Security and Privacy Protection (2017B030301004). Yu Yu is supported by the National Natural Science Foundation of China (Grant No. 61872236), the National Cryptography Development Fund (Grant No. MMJJ20170209). Shuqin Fan and Zhenfeng Zhang are supported by the National Key Research and Development Program of China (Grant No. 2017YFB0802005).
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
A Definitions of Hard Problems
A Definitions of Hard Problems
The AMLWE Problem (with Binomial Distributions). The decisional AMLWE problem \(\mathrm {AMLWE}_{n,q,k,\ell ,\eta _1,\eta _2}\) asks to distinguish  and uniform over \(R_q^{k\times \ell } \times R_q^k\), where \({\mathbf {A}}\xleftarrow {\$}R_q^{k\times \ell }, \mathbf {s}\xleftarrow {\$}B_{\eta _1}^\ell ,\mathbf {e}\xleftarrow {\$}B_{\eta _2}^k\). Obviously, when \(\eta _1 = \eta _2\), the AMLWE problem is the standard MLWE problem.
and uniform over \(R_q^{k\times \ell } \times R_q^k\), where \({\mathbf {A}}\xleftarrow {\$}R_q^{k\times \ell }, \mathbf {s}\xleftarrow {\$}B_{\eta _1}^\ell ,\mathbf {e}\xleftarrow {\$}B_{\eta _2}^k\). Obviously, when \(\eta _1 = \eta _2\), the AMLWE problem is the standard MLWE problem.
The AMLWE-R Problem. The AMLWE-R problem  asks to distinguish
asks to distinguish

from  , where
, where  .
.
The AMSIS Problem. Given a uniform matrix \(\mathbf{A} \in R_q^{k\times (\ell _1+ \ell _2 - k)}\), the (Hermite Normal Form) AMSIS problem \(\mathrm {AMSIS}^\infty _{n,q,k,\ell _1,\ell _2,\beta _1,\beta _2}\) over ring \(R_q\) asks to find a non-zero vector \(\mathbf{x} \in R_q^{\ell _1+\ell _2}\backslash \{\mathbf {0}\}\) such that \((\mathbf {I}_k\Vert {\mathbf {A}}) \mathbf {x}=\mathbf {0}\bmod q\), \(\Vert \mathbf {x}_1\Vert _\infty \le \beta _1\) and \(\Vert \mathbf {x}_2\Vert _\infty \le \beta _2\), where \(\mathbf {x}= \left( \begin{array}{c} \mathbf {x}_1 \\ \mathbf {x}_2\end{array}\right) \in R_q^{\ell _1 + \ell _2},\mathbf {x}_1\in R_q^{\ell _1}, \mathbf {x}_2\in R_q^{\ell _2}\).
The AMSIS-R Problem. Given a uniformly random matrix \(\mathbf{A} \in R_q^{k\times (\ell _1+ \ell _2 - k)}\) and a uniformly random vector \(\mathbf{t}\in R_q^k\), the (Hermite Normal Form) AMSIS-R problem \(\text { AMSIS-R}_{n,q,d, k,\ell _1,\ell _2,\beta _1,\beta _2}^{\infty }\) over ring \(R_q\) asks to find a non-zero vector \(\mathbf{x} \in R_q^{\ell _1+\ell _2+1}\backslash \{\mathbf {0}\}\) such that \(\left( \mathbf {I}_k\Vert {\mathbf {A}}\Vert \mathbf{t}_1\cdot 2^d\right) \mathbf {x}=\mathbf {0}\bmod q\), \(\Vert \mathbf {x}_1\Vert _\infty \le \beta _1\), \(\Vert \mathbf {x}_2\Vert _\infty \le \beta _2\) and \(\Vert x_3\Vert _\infty \le 2\), where \(\mathbf {x}= \left( \begin{array}{c} \mathbf {x}_1 \\ \mathbf {x}_2 \\ x_3\end{array}\right) \in R_q^{\ell _1 + \ell _2+1},\mathbf {x}_1\in R_q^{\ell _1}, \mathbf {x}_2\in R_q^{\ell _2}, x_3\in R_q\) and \((\mathbf{t}_1, \mathbf{t}_0)={\mathsf{Power2Round}_{q}}{(\mathbf{t}, d)}\).
The SelfTargetAMSIS Problem. Let \(\mathsf{H}: \{0, 1\}^{*} \rightarrow B_{60}\) is a (quantum) random oracle. Given a uniformly random matrix \(\mathbf{A} \in R_q^{k\times (\ell _1+ \ell _2 - k)}\) and a uniform vector \(\mathbf{t}\in R_q^k\), the SelfTargetAMSIS problem \(\text {SelfTargetAMSIS}_{n,q, k,\ell _1,\ell _2,\beta _1,\beta _2}^{\infty }\) over ring \(R_q\) asks to find a vector \(\mathbf{y} = \left( \begin{array}{c} \mathbf {y}_1 \\ \mathbf {y}_2 \\ c \end{array}\right) \) and \(\mu \in \{0, 1\}^{*} \), such that \({\Vert }{\mathbf {y}_1}{\Vert }_\infty \le \beta _1\), \({\Vert }{\mathbf {y}_2}{\Vert }_\infty \le \beta _2\), \({\Vert }{c}{\Vert }_\infty \le 1\) and  holds.
holds.
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Zhang, J., Yu, Y., Fan, S., Zhang, Z., Yang, K. (2020). Tweaking the Asymmetry of Asymmetric-Key Cryptography on Lattices: KEMs and Signatures of Smaller Sizes. In: Kiayias, A., Kohlweiss, M., Wallden, P., Zikas, V. (eds) Public-Key Cryptography – PKC 2020. PKC 2020. Lecture Notes in Computer Science(), vol 12111. Springer, Cham. https://doi.org/10.1007/978-3-030-45388-6_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-45388-6_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45387-9
Online ISBN: 978-3-030-45388-6
eBook Packages: Computer ScienceComputer Science (R0)





 and
and 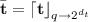 . Then, return the public key
. Then, return the public key  and the secret key
and the secret key  and a plaintext
and a plaintext 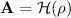 ,
,  , and return the ciphertext
, and return the ciphertext 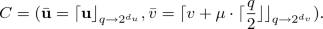
 . Then, return the public key
. Then, return the public key 
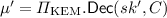 and
and  . Return the public key
. Return the public key 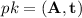 and secret key
and secret key 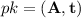 , a message
, a message 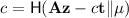 , and 0 otherwise.
, and 0 otherwise. . Return the public key
. Return the public key 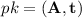 and secret key
and secret key  , a message
, a message  , otherwise return 0.
, otherwise return 0. . Return the public key
. Return the public key  and secret key
and secret key 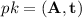 , a message
, a message 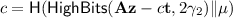 , otherwise return 0.
, otherwise return 0. and
and  and secret key
and secret key  or
or  or
or  or the number of 1’s in
or the number of 1’s in  and the number of 1’s in
and the number of 1’s in 