Abstract
Although Byzantine Agreement (BA) has been studied for three decades, perhaps somewhat surprisingly, there still exist significant gaps in our understanding regarding its round complexity. A long-standing open question is the following: can we achieve BA with sublinear round complexity under corrupt majority? Due to the beautiful works by Garay et al. (FOCS’07) and Fitzi and Nielsen (DISC’09), we have partial and affirmative answers to this question albeit for the narrow regime \(f = n/2 + o(n)\) where f is the number of corrupt nodes and n is the total number of nodes. So far, no positive result is known about the setting \(f > 0.51n\) even for static corruption!
In this paper, we make progress along this somewhat stagnant front. We show that there exists a corrupt-majority BA protocol that terminates in \(O(\frac{1}{\epsilon } \log \frac{1}{\delta })\) rounds in the worst case, satisfies consistency with probability at least \(1 - \delta \), and tolerates \((1-\epsilon )\) fraction of corrupt nodes. Our protocol secures against an adversary that can corrupt nodes adaptively during the protocol execution but cannot perform “after-the-fact” removal of honest messages that have already been sent prior to corruption. Our upper bound is optimal up to a logarithmic factor in light of the elegant \(\varOmega (1/\epsilon )\) lower bound by Garay et al. (FOCS’07).
T.-H. Hubert Chan is partially supported by the Hong Kong RGC under the grant 17200418.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
A central abstraction in distributed systems and cryptography is Byzantine Agreement (BA), where a designated sender aims to communicate a bit to multiple receivers. We require two security properties, consistency and validity. Consistency requires that all honest nodes output the same bit; and validity requires that they all output the sender’s bit if the sender is honest. Since the beginning of distributed computing, a foundational and important question is the round complexity of Byzantine Agreement. A line of elegant works have investigated this question. The celebrated work of Dolev and Strong [11] showed that there exists an \((f+1)\)-round BA protocol that tolerates up to f Byzantine corruptions for any \(f < n\). Further, they showed that \(f+1\) rounds is optimal for deterministic protocols. Subsequently, it was shown that randomized protocols can overcome this \(f+1\) round complexity lower bound: specifically, a sequence of works [2, 12, 21], beginning with Feldman and Micali [12]’s ingenious work, showed the existence of expected constant-round protocols in the honest-majority setting.
Now, an important question is whether we can achieve similar results for the corrupt majority setting, i.e., can randomized protocols help us overcome the \((f+1)\)-round complexity lower bound when the majority of nodes can be corrupt?
Perhaps somewhat surprisingly, despite decades of research on Byzantine Agreement, our understanding of this fundamental question remains limited. To the best of our knowledge, the only known results prior to our work are restricted to very narrow parameter regimes, that is, when the number of corrupt nodes is just a little more than 1/2. Specifically, Fitzi and Nielsen [13] showed that if the number of corrupt nodes is \(n/2 + k\), then an O(k)-round (randomized) BA protocol exists assuming the existence of a PKI and secure signatures (and their work improves the earlier result by Garay et al. [14]). In other words, so far we only know how to construct sublinear-round BA protocols in the corrupt majority setting when the number of corruptions is \(n/2 + o(n)\).
1.1 Our Results and Contributions
We make progress along this somewhat stagnant front. We show a positive result in the corrupt majority setting assuming the existence of a public-key infrastructure and standard cryptographic assumptions. For any \(0< \epsilon , \delta < 1\), suppose that the adversary corrupts at most \((1-\epsilon ) n\) nodes and runs in time polynomial in some security parameter \(\kappa \), then we can construct a BA protocol that reaches agreement in \(O(\log (1/\delta )/\epsilon )\) number of rounds with probability \(1 - \delta - \mathsf{negl}(\kappa )\) where \(\mathsf{negl}(\kappa )\) is a negligibly small function in \(\kappa \) corresponding to the probability that the cryptographic primitives employed are broken.
Remark 1
Typically, one requires that the protocol’s (statistical) failure probability \(\delta \) be a negligible function in some statistical security parameterFootnote 1 \(\lambda \): in this typical case, the reader can think of \(\log (1/\delta )\) as being polylogarithmic in \(\lambda \) (and independent of n).
Our result is almost optimal in light of an elegant round-complexity lower bound for randomized Byzantine Agreement (BA) by Garay et al. [14]. Specifically, they show that any randomized BA protocol (allowing up to constant failure probability) must consume \(\varOmega (n / (n-f))\) rounds—note that for \(f = (1-\epsilon ) n\), the lower bound becomes \(\varOmega (1/\epsilon )\). In comparison, our upper bound is optimal up to a \(\log (1/\delta )\) factor.
Note that our result allows for \(\epsilon \) to be a function in n. For example, for \(\epsilon = O(1)\), we give an \(O(\log (1/\delta ))\)-round protocol; and for \(\epsilon = O(1/\sqrt{n})\), we give an \(O(\sqrt{n} \cdot \log (1/\delta ))\)-round protocol. Finally, for any \(f \le n - \omega ({\log (1/\delta )})\), we achieve sublinear (in n) number of rounds which is asymptotically better than the celebrated Dolev-Strong protocol [11].
Theorem 1
(Nearly round-optimal protocols for corrupt majority). Assume the existence of a public-key infrastructure (PKI) and standard cryptographic assumptions. For parameters \(\epsilon , \delta \in (0, 1)\) which are allowed to be functions in n, there exists a protocol that terminates in \(O(\log (1/\delta )/\epsilon )\) number of rounds and achieves BA with \(1-\delta - \mathsf{negl}(\kappa )\) probability in the presence of an adversary that adaptively corrupts at most \((1-\epsilon )n\) nodes and runs in time polynomial in \(\kappa \).
We stress that previously, except for the narrow parameter regime \(f = 0.5n + o(n)\), no sublinear-round protocol is known for the corrupt majority setting, not even under static corruption and making any conceivable assumption including very strong ones such as random oracles and the ability of honest nodes to erase secrets from memory. Importantly, even under static corruption, the standard random committee election technique that is commonly adopted for an honest-majority setting [1, 3, 19, 23, 24] fails for corrupt majority for reasons we will explain later in this section as well as Sect. 3.1! Our protocol works in a model where the adversary may adaptively corrupt nodes in the middle of the execution, as long as the adversary cannot retroactively erase messages that were already sent before the corruption took place [1].
Finally, to aid understanding of Theorem 1, we remark that the existence of a public-key infrastructure is long known to be necessary for achieving BA under corrupt majority—without any setup assumptions, BA is not possible under 1/3 or more corruptions [25].
Technical Highlights. In an honest majority setting assuming static corruption, a standard technique [1, 3, 19, 23, 24] is to elect a random, polylogarithmically sized committee to run a round-inefficient BA protocol; and non-committee members will decide on a value that is vouched for by the majority of the committee. It is tempting to think that the same technique will work for a corrupt majority setting but this intuition turns out to be wrong because majority voting no longer works here.
Our approach adopts a two-step recipe. First, we describe a new technique that combines the random committee election idea with the well-known Dolev-Strong protocol [11], but in a non-blackbox manner to allow non-committee members who do not have voting power to keep committee members informed of their latest local state during the consensus. With this technique, we can construct an \(O(\log (1/\delta )/\epsilon )\)-round BA protocol secure against \((1-\epsilon )n\) static corruptions. Even this static-corruption result is new and advances the state-of-the-art regarding the round complexity of BA under corrupt majority.
Next, we describe a technique to upgrade our protocol to defend against even an adaptive adversary. The challenge here is that if the random committee is elected a priori, an adaptive adversary can simply corrupt the entire committee. To defend against such an adversary, we employ adaptively secure Verifiable Random Functions (VRFs) to secretly elect a committee, such that the committee is not revealed until they need to cast votes in the protocol. Not only so, an important technical subtlety is that the committee election must be bit-specific, i.e., the committee that is allowed to vote on 0 is elected independently from the committee that is allowed to vote on 1—otherwise, upon observing some committee members voting for 0, the adaptive adversary can immediately corrupt these nodes and make them vote for 1 too (and it turns out that such an attack can break both consistency and validity). Bit-specific committee election is a new technique that was first described in the very recent works by Abraham et al. [1] (PODC’19) and Chan et al. [5] (Eurocrypt’19) where they focus on constructing adaptively secure, bandwidth-efficient consensus protocols. Interestingly, while existing works [1, 5] rely on this technique to improve the bandwidth consumption of adaptively secure BA under honest majority, we are the first to use these techniques to achieve a non-trivial round complexity result for corrupt majority.
Last but not the least, our techniques for achieving these results are in fact conceptually simpler than those of Fitzi and Nielsen [13] (which is an improvement of Garay et al. [14]); and moreover, our results apply to a broad parameter regime whereas the prior works [13, 14] only achieve sublinear-round for the narrow regime \(f < n/2 + o(n)\). We view the conceptual simplicity as an advantage of our approach.
Open Questions. Although our work advances the state-of-the-art in a fundamental area that has been somewhat stagnant, we still have not completely closed the gap in our understanding. Some interesting open questions remain.
-
For example, can we achieve sublinear-round BA under corrupt majority with a strongly adaptive adversary who is even allowed to remove messages sent by an honest node in round r by adaptively corrupting the node in the same round? Many earlier works in the BA literature in fact consider such a strongly adaptive adversary [4, 11, 16, 21, 23].
-
Another interesting question is whether we can weaken the setup assumptions needed to get such a result. Specifically, observe that the setup assumptions we need are slightly stronger than that of Dolev and Strong [11].
-
For honest majority, expected constant round BA is known [1, 2, 12, 21]. The protocols in this paper are not expected constant round. Therefore, an interesting direction is whether we can have expected constant round protocols in the corrupt majority setting—note that due to the lower bound by Garay et al. [14], this can only be possible if constant fraction of the nodes are corrupt.
We leave these directions for future work.
Additional Related Work. Several other works [8, 20] proved lower bounds on the worst-case round complexity of randomized BA; and the online full version of this paper [6] presented complete proofs of these lower bounds. Note that these lower bounds are incomparable to Garay et al.’s lower bound [14]. Cohen et al. [10] prove lower bounds on the round complexity of randomized Byzantine agreement (BA) protocols, bounding the halting probability of such protocols after one and two rounds.
A line of works in the literature [9, 15, 18] have focused on a simulation-based notion of adaptive security for Byzantine Broadcast, where the concern is that the adversary should not be able to observe what the sender wants to broadcast, and then adaptively corrupt the sender to flip the bit. This notion is stronger than what we consider in this paper, but such a strong notion was only achieved earlier by making stronger assumptions than in our paper [15], i.e., the “atomic message” model: after adaptively corrupting a node i, the adversary not only is unable to erase a message i already sent in this round, but also must wait for at least one maximum network delay before the corrupt i can start sending corrupt messages.
2 Preliminaries
2.1 Protocol Execution Model
We assume a standard protocol execution model with n nodes indexed with \([n] := \{1, 2, \ldots , n\}\). An external party called the environment and denoted \({{\mathcal {Z}}} \) provides inputs to honest nodes and receives outputs from the honest nodes. An adversary denoted \({\mathcal {A}} \) controls a subset of the nodes which are said to be corrupt; all other nodes are said to be honest. All corrupt nodes are under the control of \({\mathcal {A}} \), i.e., the messages they receive are forwarded to \({\mathcal {A}} \), and \({\mathcal {A}} \) controls what messages they will send once they become corrupt. The adversary \({\mathcal {A}} \) and the environment \({{\mathcal {Z}}} \) are allowed to freely exchange messages any time during the execution. To capture protocols that employ cryptography, we assume that all nodes as well as \({\mathcal {A}} \) and \({{\mathcal {Z}}} \) are Interactive Turing Machines that run in time polynomial in some security parameter \(\kappa \); further, we assume that \(\kappa \) is known to all nodes as well as \({\mathcal {A}} \) and \({{\mathcal {Z}}} \).
We assume a standard synchronous network model. Whenever honest nodes send a message, the message is delivered to honest recipients at the beginning of the next round.
Adaptivity of the Adversary. We shall assume an adaptive adversary that can corrupt nodes in the middle of the execution. The adversary can observe all currently honest nodes’ messages in round r before deciding which subset of these nodes to corrupt in round r. Suppose an honest node P sends a message in some round r and then becomes corrupt in the same round—in this case we assume that the adversary cannot perform “after-the-fact” removal and a-posteriori delete the message that was sent by P in round r before it became corrupt. However, since P is corrupt, the adversary may now inject additional round-r messages on behalf of P.
For ease of understanding, in our exposition we will first describe a warmup protocol secure against a static adversary: such an adversary is required to declare the set of corrupt nodes before the start of the execution.
2.2 Byzantine Agreement
In this section we formally define Byzantine Agreement. Recall that there are n nodes indexed by \(\{0, 1, 2, \ldots , n-1\}\). Without loss of generality, we shall assume that node 0 is the designated sender.
Syntax. Before the protocol starts, the sender receives an input \(b \in \{0, 1\}\) from the environment \({{\mathcal {Z}}} \). At the end of the protocol, every node i (including the sender) outputs a bit \(b_i\) to the environment \({{\mathcal {Z}}} \).
Security Definition. We say that a protocol (satisfying the above syntax) achieves BA with probability p with respect to \(({\mathcal {A}}, \mathcal {Z})\), iff with probability at least p over the choice of the randomized execution, the following properties are satisfied:
-
Consistency. If an honest node outputs \(b_i\) and another honest node outputs \(b_j\) to \({{\mathcal {Z}}} \), then it must hold that \(b_i = b_j\).
-
Validity. If the designated sender remains honest throughout and its input is b, then any honest node’s output to \({{\mathcal {Z}}} \) must be b.
3 Technical Roadmap: Nearly Round-Optimal BA for Corrupt Majority
In this section, we give a slightly informal presentation of our construction. Later on in Sects. 4 and 5, we present a formal description along with formal proofs.
3.1 Warmup: Any Constant Fraction of Static Corruption
For simplicity, let us first focus on the simpler case when the adversary is constrained to making static corruptions. Let \(\epsilon \) denote the fraction of honest nodes, where \(\epsilon \) can potentially be a function of n; however, as a warmup, we assume \(\epsilon \) to be some arbitrarily small constant in this section. We will later extend our approach to more general choices of \(\epsilon \) and to the case of adaptive corruptions. We stress, however, that except for the narrow parameter regimes in Garay et al.’s result [14], previously it was unknown how to achieve sublinear-round BA in the corrupt majority setting even assuming static corruptions. We use \(\delta > 0\) to denote the failure probability (for consistency).
Flawed Strawman Approach. One tempting but flawed approach is to randomly elect a small committee of \(\log (1/\delta )\) nodes—for the time being, imagine that a random leader election oracle exists—and have the committee run a corrupt-majority BA protocol such as Dolev-Strong [11]. For the special case \(\epsilon = \varTheta (1)\) and static corruption, it is not hard to show that except with \(O(\delta )\) probability, the committee consists of at least 1 honest node. Thus all honest nodes within the small committee can reach agreement on a bit \(b^*\) in \(\log (1/\delta )\) number of rounds. Unfortunately, there does not seem to be any straightforward way to securely convey this bit to the non-committee nodes (note that the common approach of taking a majority vote among the committee fails to work in the corrupt majority setting).
To resolve this challenge, our insight is to combine the random committee election idea and the Dolev-Strong protocol in a non-blackbox manner.
Background: the Dolev-Strong Protocol. We start by reviewing the classical Dolev-Strong protocol [11] that achieves linear round complexity and tolerates any number of corruptions—henceforth the term “multicast” means “send to everyone”Footnote 2:
-
Every node i maintains an \(\mathsf{Extracted}_i\) set that is initialized to be empty. In round 0, the sender signs its input bit b, and multicasts b and the signature.
-
For each round \(r = 1 \ldots n\): for each bit \(b \in \{0, 1\}\), if node i has observed valid signatures on b from at least r distinct nodes including the designated sender and \(b \notin \mathsf{Extracted}_i\): compute a signature on b; multicast b and all signatures it has observed on b (including its own); include b in \(\mathsf{Extracted}_i\).
-
At the end of the protocol, each node i outputs the bit contained in \(\mathsf{Extracted}_i\) if \(|\mathsf{Extracted}_i| = 1\); else it outputs a canonical bit 0.
This protocol retains consistency, if the number K of rounds is strictly larger than the number f of (eventually) corrupt nodes. First, if an honest node i first adds a bit b to its \(\mathsf{Extracted}_i\) set in any round \(r < K\), then by the end of round \(r+1\), b must be in every honest node’s \(\mathsf{Extracted}\) set. Further, if a honest node i first adds a bit b to its \(\mathsf{Extracted}_i\) set in the last round K (which is at least \(f+1\)), then at least one out of the \(K \ge f+ 1\) signatures it has observed in round K must be from an honest node—it holds that this honest node must have added b to its \(\mathsf{Extracted}\) set in some round \(r < K\) before the last round; and thus by the end of the last round K, every honest node will have b in its \(\mathsf{Extracted}\) set.
Achieving Agreement for Non-committee Members. Recall that the problem with the naïve committee election approach is how to convey the committee’s decision to the non-committee members. To this end we will combine the committee election idea with Dolev and Strong’s protocol in a non-blackbox manner. Suppose that a leader election oracle exists that helps us elect a committee of \(\log (1/\delta )\) nodes after the adversary chooses the corrupt nodes. As argued earlier, except with probability \(O(\delta )\), there is at least one honest node in the committee.
Henceforth we assume that only the committee members are authorized signers and signatures from any non-committee node will be ignored. Our key insight is to divide each round r of the Dolev-Strong protocol into two mini-rounds:
-
Every node i maintains an \(\mathsf{Extracted}_i\) set that is initialized to be empty. In round 0, the sender signs its input bit b, and multicasts b and the signature.
-
For each round \(r = 1, 2, \ldots , S + 1\) where \(S = \log (1/\delta )\) denotes the committee size,
-
1.
In the first mini-round, if any node i receives a bit \(b \notin \mathsf{Extracted}_i\) with r signatures from distinct signers, it adds b to \(\mathsf{Extracted}\) and multicasts b tagged with all signatures observed so far for b.
-
2.
In the second mini-round, only the committee members perform the actions above and moreover a committee member always appends its own signature for b when multicasting b (and all other seen signatures on b).
-
1.
-
Each node i outputs the bit contained in \(\mathsf{Extracted}_i\) if \(|\mathsf{Extracted}_i| = 1\); else it outputs a canonical bit 0.
Note that this approach guarantees that if any honest node newly adds a bit b to its \(\mathsf{Extracted}\) set in round r, then all committee nodes must have signed it by the end of round r (if not earlier) and multicast the corresponding signature. Thus in the first mini-round of round \(r+1\), every honest node will have added b to its \(\mathsf{Extracted}\) set. At this moment, it is not difficult to see that as long as one committee member is honest, if the above protocol is executed for at least \(f+1\) rounds then we can argue consistency using a similar approach as Dolev-Strong.
3.2 Achieving Adaptive Security and Removing the Leader Election Oracle
The above protocol enables the committee to securely convey its decision to non-committee nodes; unfortunately, the protocol does not defend against adaptive corruptions. Specifically, since the elected committee is small relative to n, an adaptive adversary can simply corrupt all committee members after they are elected. We now present an approach for achieving adaptive security borrowing the “bit-specific committee election” idea that was previously employed in the construction of small-bandwidth honest-majority BA protocols by Abraham et al. [1] and Chan et al. [5]. As a by-product we will have instantiated the leader election oracle that was needed earlier.
Our idea is to tie the committee election to each individual bit, i.e., there is a separate committee that are allowed to vote on 0 and 1 respectively (henceforth called the 0-committee and the 1-committee respectively), and the designated sender is in both committees. Specifically, Abraham et al. [1] and Chan et al. [5] describe how to realize bit-specific committee election using a suitable Verifiable Random Function (VRF) with adaptive security. Take \(b = 0\) as an example. For a node i to determine if he is on the 0-committee, he checks the following:
Here \(\mathsf {sk}_i\) is his private key, \(D_p\) is an appropriate difficulty parameter that determines the success probability (denoted p) of each election attempt, and \(\pi \) is a proof generated by the VRF which will be used below for verification. Concretely, the probability p is chosen such that the expected number of nodes elected into either the 0-committee or 1-committee is \(\log (1/\delta )\). To convince others that i is indeed an eligible member of the 0-committee, i reveals both \(\rho \) and \(\pi \), and everyone can now verify, using i’s public key, that indeed \(\rho \) is the correct outcome of the VRF.
We now explain how to use bit-specific committee election to achieve adaptive security. Suppose a 0-committee member i becomes immediately corrupt after signing 0 and multicasting signatures on 0. However, corrupting node i does not necessarily help voting for the bit 1—in particular, since the two committees are independently selected, node i is only as good as any other node in terms of its likelihood of being elected into the 1-committee. Thus, corrupting node i is only as good as corrupting any other node at this point. In the proof of Lemma 2, we will formalize the above intuition.
Putting it Altogether. We say that a tuple \((b, i, \pi )\) is a valid vote on b iff either (1) \(i = 1\) is the designated sender and \(\pi \) is a valid signature on b from i; or (2) \(i\ne 1\) and \(\pi \) is a valid VRF proof proving i to be in the b-committee. The protocol is described below.
-
Every node i initializes \(\mathsf{Extracted}_i := \emptyset \). The sender signs its input bit b and multicasts b as well as the signature.
-
For round \(r = 1, \ldots , \log (1/\delta )\), every node i performs the following:
-
1.
First mini-round: for every \(b \notin \mathsf{Extracted}_i\) such that the node has observed at least r votes from distinct nodes including the sender: add b to \(\mathsf{Extracted}_i\); multicast b and all observed votes on b.
-
2.
Second mini-round: for every \(b \notin \mathsf{Extracted}_i\), if node i belongs to the b-committee and moreover the node has observed at least r votes from distinct nodes including the sender: add b to \(\mathsf{Extracted}_i\); compute a new vote on b; multicast b and all observed votes on b (including the newly created one).
-
1.
-
Every node i outputs the bit contained in \(\mathsf{Extracted}_i\) if \(|\mathsf{Extracted}_i| = 1\); else output a canonical bit 0.
3.3 Organization of the Subsequent Formal Sections
The subsequent sections formalize the description contained in this section. Specifically, in Sect. 4, we describe an idealized version of the protocol assuming an ideal eligibility election oracle, and we conduct stochastic analysis of the idealized protocol for more general choices of \(\epsilon \). Next, in Sect. 5, we describe how to replace the idealized leader eligibility election oracle with suitable adaptively secure cryptographic primitives, and yet retain the security properties of the idealized protocol.
4 Formal Description of  -Hybrid Protocol
-Hybrid Protocol
In the sections to follow, we will formally present our upper bound for the corrupt majority case. We will first describe our protocol assuming an idealized oracle called \(\mathcal {F}_\mathrm{mine}\) that is in charge of random eligibility electionFootnote 3—this approach allows us to “abstract away” the cryptography and focus on analyzing the stochastic properties of the protocol first. Later in Sect. 5, we will show how to leverage standard techniques to remove the \(\mathcal {F}_\mathrm{mine}\) assumption and instantiate it with appropriate, adaptively secure cryptography.
Henceforth, to make our description and proofs more precise, we define some additional terminology. At any time in the protocol, nodes that remain honest so far are referred to as so-far honest nodes; nodes that remain honest till the end of the protocol are referred to as forever honest nodes.
4.1 Ideal Functionality 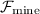 for Random Eligibility Determination
for Random Eligibility Determination
The idealized oracle \(\mathcal {F}_\mathrm{mine}\) provides the following functionality. A node i can query \(\mathcal {F}_\mathrm{mine}\) to check if it is an eligible member of the b-committee where \(b \in \{0, 1\}\). Upon receiving such a query, \(\mathcal {F}_\mathrm{mine}\) flips a random coin (with appropriate probability) to determine the answer; further \(\mathcal {F}_\mathrm{mine}\) stores this answer and returns it to any node that queries it henceforth.
More formally, the \(\mathcal {F}_\mathrm{mine}\) ideal functionality has two activation points:
-
Whenever a node i calls \(\mathtt{mine}(b)\) for the first time where \(b \in \{0, 1\}\), \(\mathcal {F}_\mathrm{mine}\) flips a random coin (parametrized with an appropriate probability p) to decide if i is a committee member for b.
Henceforth if a node i calls \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(b)\), we also say that i makes a mining attempt for the bit b.
-
If node i has called \(\mathtt{mine}(b)\) and the attempt is successful, anyone who calls \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{verify}(b, i)\) will obtain an answer of 1; all other calls to \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{verify}(b, i)\) will return 0.
Henceforth in the paper, we assume that the choice of the success probability p is a global, public parameter. We will describe how to choose p later.
Our protocol. The protocol is described in the \(\mathcal {F}_\mathrm{mine}\)-hybrid world. Section 5 will explain how to instantiate \(\mathcal {F}_\mathrm{mine}\) with cryptographic assumptions.
4.2 Formal Protocol in the  -Hybrid World
-Hybrid World
We describe how to achieve adaptively secure BA with sublinear round complexity, tolerating \(1-\epsilon \) fraction of corruption for any arbitrarily small positive constant \(\epsilon \). Recall that without loss of generality, we assume that node 0 is the designated sender.
Valid Vote. With respect to some moment in time, a valid vote for the value b from node i is of the following form:
-
If \(i = 0\), i.e., i is the sender, then a valid vote is of the form \((b, 0, \mathtt{Sig}_0(b))\), where \(\mathtt{Sig}_0(b)\) denotes a valid signature from the sender on the bit b.
-
For \(i \ne 0\), a valid vote w.r.t. some time t is of the form (b, i) such that \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{verify}(b,i)\) returns 1 at time t, i.e., by time t, node i must have called \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(b)\) and the result must have been successful.
Valid Vote Batch. For \(r \ge 1\), a valid r-batch of votes for value b consists of valid votes for value b from r distinct nodes, one of which must be the sender 0. Note that just like the definition of a valid vote, a valid vote batch is also defined w.r.t. to some moment of time (which we sometimes omit writing explicitly if the context is clear).
Since we have explained the intutition behind our protocol earlier, we now give a formal presentation of the protocol in Fig. 1—here “multicast” means sending a message to everyone.
4.3 Analysis in the  -Hybrid World
-Hybrid World
In this subsection, we shall prove the following theorem for our \(\mathcal {F}_\mathrm{mine}\)-hybrid-world protocol described in Fig. 1.
Theorem 2
Assume that the signature scheme is secure. For any \(0< \epsilon , \delta < 1\) (that can be functions of n), the \(\mathcal {F}_\mathrm{mine}\)-hybrid Byzantine agreement protocol described in Fig. 1 satisfies consistency (with probability at least \(1 - \delta \)) and validity and terminates in \(2 \cdot \lceil \frac{3}{\epsilon } \ln \frac{2}{\delta } \rceil \) rounds (with probability 1) w.r.t. any non-uniform \(\text {p.p.t.}\) \(({\mathcal {A}}, {{\mathcal {Z}}})\) that corrupts no more than \((1-\epsilon )n\) nodes.
Committee. Without loss of generality, we consider a modification to the protocol, where \(\mathcal {F}_\mathrm{mine}\) flips a coin for each (b, i) pair upfront. When \(\mathcal {F}_\mathrm{mine}\) receives \(\mathtt{mine}\) queries, it simply retrieves the corresponding coin that has already been flipped earlier. In this world, we can define the notion of committees more easily: For each bit b, a node \(i \ne 1\) is in the committee \(\mathtt{Com}_b\) for b, if \({\mathsf{Coin}} [b, i] = 1\).
Honest and Corrupt Votes. A (valid) vote for a bit b from a node i is said to be honest if the node is so-far honest at the moment the vote is cast, which is the moment when node i calls \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(b)\); otherwise, the (valid) vote is said to be corrupt or dishonest.
Handling Signature Failure. Assume that the signature scheme is secure, and that \({\mathcal {A}} \) and \({{\mathcal {Z}}} \) are probabilistic polynomial time, it must hold that except with negligible probability, no so-far honest node should have a forged signature in view. This is formalized in the following fact:
Fact 1
(No signature failure). Assume that the signature scheme is secure. Then, except with negligible probability, the following holds: if the sender is so-far honest and did not sign the bit \(b \in \{0, 1\}\), then no so-far honest node has seen a valid signature on b from the sender.
Proof
By straightforward reduction to signature security.
There are two types of bad events that can cause our protocol’s security to fail: (1) signature failure (captured by Fact 1); and (2) other stochastic bad events related to \({\mathcal {F}_\mathrm{mine}} \)’s coin flips. In the next subsection, we will bound the probability of the latter type of bad events—and there we will pretend that the signature scheme is “ideal” and there are no signature failures—but we stress that technically, we are actually taking a union bound over signature failure and the stochastic bad events analyzed in the next subsection.
Proofs: Bounding Stochastic Bad Events. The protocol clearly satisfies termination; and validity also follows trivially from Fact 1. Thus the remainder of this section will focus on the consistency proof. Our proofs work for general choices of parameters, including the honest fraction \(\epsilon \) (which can be a function of n) and the failure probability \(\delta \). As a special case, assuming that \(\epsilon \) is any arbitrarily small positive constant and moreover, the mining difficulty parameter p and the total number of stages \({R} \) are chosen as in Fig. 1, then the failure probability \(\delta = e^{-\omega (\log \kappa )}\) would be a negligible function in the security parameter \(\kappa \).
To prove consistency, we will prove that there is no discrepancy for either bit (except with \(\delta \) probability), which is formally defined as follows.
Discrepancy for b. A discrepancy for \(b \in \{0, 1\}\) occurs if at the end of the protocol there exist two honest nodes such that b is in exactly one of the two corresponding extracted sets. We further classify the following two types of discrepancy if, in addition, the following conditions are satisfied.
- Type-A.:
-
A type-A discrepancy for b occurs when b is first added to some honest node’s extracted set in some stage in \([1..{R} ]\).
- Type-B.:
-
A type-B discrepancy for value b occurs when \({R} +1\) is the only stage in which b is added to any honest node’s extracted set.
Fact 2
If an honest vote is cast for value b (at the second round of some stage) during the protocol, then for each forever honest node i, it holds at termination that \(b \in \mathsf{Extracted}_i\).
Lemma 1
(Type-A Discrepancy). Suppose the probability of success for \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(\cdot )\) is \(p := \min \{1, \frac{1}{\epsilon n} \cdot \log \frac{1}{\delta } \}\). For any value b, a type-A discrepancy for value b happens with probability at most \(\delta \).
Proof
It suffices to prove the claim that if a type-A discrepancy for value b occurs, then there are at least \(\epsilon n\) nodes, each of which has called \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(b)\) with unsuccessful result at some moment when it is still so-far honest. For the trivial case \(e^{-\epsilon n} \ge \delta \), we have \(p = 1\) and every mining attempt must be successful. For the case \(e^{-\epsilon n} < \delta \), this event happens with probability at most \((1 - p)^{\epsilon n} \le \exp (- \epsilon n p) \le \delta \), which implies the result of the lemma.
The rest of the proof establishes the above claim. Observe that a type-A discrepancy implies that at some moment, there is a first time when a so-far honest node adds b to its extracted set in some stage \(r \in [1..{R} ]\). If this happened in the second round of stage r, then this so-far honest node is in \(\mathtt{Com}_b\) and would have been able to cast a valid \((r+1)\)-batch of votes that can be seen by everyone in stage \(r+1\). Therefore, a type-A discrepancy means that b is first added to a so-far honest node i in the first round of stage r, which means node i has seen some valid r-batch of votes.
Since this node i is so-far honest, it will multicast this batch to everyone, and every so-far honest node that has not tried to call \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(b)\) before will call \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(b)\) in the second round of stage r.
Since a type-A discrepancy occurs, it must be case that all (previous or present) trials of \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(b)\) by so-far honest nodes have returned unsuccessful. Since at any moment, the number of so-far honest nodes is at least \(\epsilon n\), we conclude that the claim is true, and this completes the proof.
Fact 3
(Chernoff Bound). Suppose X is the sum of independent \(\{0,1\}\)-random variables. Then, for any \(\tau > 0\), the following holds:
Lemma 2
(Type-B Discrepancy). Let \(p := \min \{1, \frac{1}{\epsilon n} \log \frac{1}{\delta } \}\) as in Lemma 1, and set \({R}:= \lceil \frac{3}{\epsilon } \cdot \ln \frac{1}{\delta } \rceil \). Then, for any value b, a type-B discrepancy for b happens with probability at most \(\delta \).
Proof
A type-B discrepancy for b occurs implies that some honest node i sees a valid \(({R} +1)\)-batch of votes, which are all cast by dishonest nodes. This is because if one of the votes was cast by a so-far honest node (in the second round) of some stage \(r \in [1..{R} ]\), then everyone would have seen a valid \((r+1)\)-batch in stage \(r+1\), in which case a discrepancy would not have occurred.
Observe that a dishonest vote is cast only if a node is corrupted before it calls \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(b)\) for the first time. There are at most \((1 -\epsilon )n\) dishonest nodes and each of them can call \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(b)\) successfully independently with probability p. Important: Note that even if nodes are corrupted adaptively (for instance, based on mining results of other values), the success probability of mining value b is still p.
For the trivial case, \(\delta \le e^{-\epsilon n}\), \({R} \ge 3n\) is not interesting; hence, it suffices to consider \(\delta > e^{-\epsilon n}\) and \(p < 1\). We next consider two cases.
-
Case \(\epsilon \ge \frac{1}{4}\). Set \(\tau := \frac{3 \epsilon }{1 - \epsilon } \ge 1\). By Chernoff Bound, the probability that there are more than \({R} = \lceil \frac{3}{\epsilon } \cdot \ln \frac{1}{\delta } \rceil \ge (1 + \tau ) (1 - \epsilon )n p\) dishonest votes is at most \(\exp (-\frac{\tau (1 - \epsilon )n p}{3}) = \delta \).
-
Case \(\epsilon < \frac{1}{4}\). Set \(\tau = 1\). By Chernoff Bound, the probability that there are more than \({R} = \lceil \frac{3}{\epsilon } \cdot \ln \frac{1}{\delta } \rceil \ge (1 + \tau ) (1 - \epsilon )n p\) dishonest votes is at most \(\exp (-\frac{(1 - \epsilon )n p}{3}) \le \delta \).
Corollary 1
Suppose that with probability 1, there are at least \(\epsilon \) fraction of forever honest nodes and let \(\delta \) be the desired failure probability. By setting the mining success probability \(p := \min \{1, \frac{1}{\epsilon n} \log \frac{2}{\delta } \}\) and \({R}:= \lceil \frac{3}{\epsilon } \cdot \ln \frac{2}{\delta } \rceil \), the protocol satisfies consistency with probability at least \(1 - \delta \).
Proof
For the trivial case \(\frac{\delta }{2} \le e^{-\epsilon n}\), the bound \(R \ge 3n\) is not interesting. Hence, it suffices to consider \(\frac{\delta }{2} > e^{-\epsilon n}\) and \(p < 1\).
To use union bound over type-A and type-B discrepancy for both values of b, we set the failure probability to be \(\frac{\delta }{2}\) in Lemmas 1 and 2.
5 Removing the Idealized Functionality 
So far, we have assumed the existence of an \(\mathcal {F}_\mathrm{mine}\) ideal functionality. In this section, we describe how to instantiate the protocols in the real world. Our techniques follow the approach described by Abraham et al. [1]. Although this part is not a contribution of our paper, for completeness, we describe all the building blocks and the approach in a self-contained manner.
5.1 Preliminary: Adaptively Secure Non-interactive Zero-Knowledge Proofs
We use \(f({\kappa }) \approx g({\kappa })\) to mean that there exists a negligible function \(\nu ({\kappa })\) such that \(|f({\kappa }) - g({\kappa })| < \nu ({\kappa })\).
A non-interactive proof system henceforth denoted \(\mathsf{nizk} \) for an NP language \({\mathcal{L}} \) consists of the following algorithms.
-
\({\mathsf{crs}} \leftarrow \mathsf{Gen}(1^{\kappa }, {\mathcal{L}})\): Takes in a security parameter \({\kappa }\), a description of the language \({\mathcal{L}} \), and generates a common reference string \({\mathsf{crs}} \).
-
\(\pi \leftarrow \mathsf{P}({\mathsf{crs}}, {\mathsf{stmt}}, w)\): Takes in \({\mathsf{crs}} \), a statement \({\mathsf{stmt}} \), a witness w such that \(({\mathsf{stmt}}, w) \in {\mathcal{L}} \), and produces a proof \(\pi \).
-
\( b \leftarrow \mathsf{V}({\mathsf{crs}}, {\mathsf{stmt}}, \pi )\): Takes in a \({\mathsf{crs}} \), a statement \({\mathsf{stmt}} \), and a proof \(\pi \), and outputs 0 (reject) or 1 (accept).
Perfect Completeness. A non-interactive proof system is said to be perfectly complete, if an honest prover with a valid witness can always convince an honest verifier. More formally, for any \(({\mathsf{stmt}}, w) \in {\mathcal{L}} \), we have that
Non-erasure Computational Zero-Knowledge. Non-erasure zero-knowledge requires that under a simulated CRS, there is a simulated prover that can produce proofs without needing the witness. Further, upon obtaining a valid witness to a statement a-posteriori, the simulated prover can explain the simulated NIZK with the correct witness.
We say that a proof system \(({\mathsf{Gen}}, \mathsf{P}, \mathsf{V})\) satisfies non-erasure computational zero-knowledge iff there exists probabilistic polynomial time algorithms \(({\mathsf{Gen}} _0, \mathsf{P}_0, \mathsf{Explain})\) such that
where \(\mathsf{Real}({\mathsf{crs}}, {\mathsf{stmt}}, w)\) runs the honest prover \(\mathsf{P}({\mathsf{crs}}, {\mathsf{stmt}}, w)\) with randomness r and obtains the proof \(\pi \), it then outputs \((\pi , r)\); \(\mathsf{Ideal}({\mathsf{crs}} _0, {\tau } _0, {\mathsf{stmt}}, w)\) runs the simulated prover \(\pi \leftarrow \mathsf{P}_0({\mathsf{crs}} _0, {\tau } _0, {\mathsf{stmt}}, \rho )\) with randomness \(\rho \) and without a witness, and then runs \(r \leftarrow \mathsf{Explain}({\mathsf{crs}} _0, {\tau } _0, {\mathsf{stmt}}, w, \rho )\) and outputs \((\pi , r)\).
Perfect Knowledge Extration. We say that a proof system \(({\mathsf{Gen}}, \mathsf{P}, \mathsf{V})\) satisfies perfect knowledge extraction, if there exists probabilistic polynomial-time algorithms \(({\mathsf{Gen}} _1, \mathsf{Extr})\), such that for all (even unbounded) adversary \({\mathcal {A}} \),
and moreover,
5.2 Adaptively Secure Non-interactive Commitment Scheme
An adaptively secure non-interactive commitment scheme consists of the following algorithms:
-
\({\mathsf{crs}} \leftarrow \mathsf{Gen}(1^{\kappa })\): Takes in a security parameter \({\kappa }\), and generates a common reference string \({\mathsf{crs}} \).
-
\(C \leftarrow {\mathsf{com}} ({\mathsf{crs}}, v, \rho )\): Takes in \({\mathsf{crs}} \), a value v, and a random string \(\rho \), and outputs a committed value C.
-
\(b \leftarrow \mathsf{ver}({\mathsf{crs}}, C, v, \rho )\): Takes in a \({\mathsf{crs}} \), a commitment C, a purported opening \((v, \rho )\), and outputs 0 (reject) or 1 (accept).
Computationally Hiding Under Selective Opening. We say that a commitment scheme \(({\mathsf{Gen}}, {\mathsf{com}}, \mathsf{ver})\) is computationally hiding under selective opening, iff there exists a probabilistic polynomial time algorithms \(({\mathsf{Gen}} _0, {{\mathsf{com}}}_0, \mathsf{Explain})\) such that
where \(\mathsf{Real}({\mathsf{crs}}, v)\) runs the honest algorithm \({\mathsf{com}} ({\mathsf{crs}}, v, r)\) with randomness r and obtains the commitment C, it then outputs (C, r); \(\mathsf{Ideal}({\mathsf{crs}} _0, {\tau } _0, v)\) runs the simulated algorithm \(C \leftarrow \mathsf{comm}_0({\mathsf{crs}} _0, {\tau } _0, \rho )\) with randomness \(\rho \) and without v, and then runs \(r \leftarrow \mathsf{Explain}({\mathsf{crs}} _0, {\tau } _0, v, \rho )\) and outputs (C, r).
Perfectly Binding. A commitment scheme is said to be perfectly binding iff for every \({\mathsf{crs}} \) in the support of the honest CRS generation algorithm, there does not exist \((v, \rho ) \ne (v', \rho ')\) such that \({\mathsf{com}} ({\mathsf{crs}}, v, \rho ) = {\mathsf{com}} ({\mathsf{crs}}, v', \rho ')\).
Theorem 3
(Instantiation of our NIZK and commitment schemes [17]). Assume standard bilinear group assumptionsFootnote 4. Then, there exists a proof system that satisfies perfect completeness, non-erasure computational zero-knowledge, and perfect knowledge extraction. Further, there exist a commitment scheme that is perfectly binding and computationally hiding under selective opening.
Proof
The existence of such a NIZK scheme was shown by Groth et al. [17] via a building block that they called homomorphic proof commitment scheme. This building block can also be used to achieve a commitment scheme with the desired properties.
NP Language Used in Our Construction. In our construction, we will use the following NP language \({\mathcal{L}} \). A pair \(({\mathsf{stmt}}, w) \in {\mathcal{L}} \) iff
-
parse \({\mathsf{stmt}}:= (\rho , c, {\mathsf{crs}} _\mathrm{comm}, b)\), parse \(w := (\mathsf {sk}, s)\);
-
it must hold that \(c = \mathsf{comm}({\mathsf{crs}} _\mathrm{comm}, \mathsf {sk}, s)\), and \(\mathsf{PRF} _{\mathsf {sk}}(b) = \rho \).
5.3 Removing  with Cryptography
with Cryptography
Cryptographic Building Blocks. We can remove the \(\mathcal {F}_\mathrm{mine}\) oracle by leveraging cryptographic building blocks including a pseudorandom function family, a non-interactive zero-knowledge proof system that satisfies computational zero-knowledge and computational soundness, and a perfectly binding and computationally hiding commitment scheme.
Compiler from Ideal-World Protocol to a Real-World Protocol. Essentially, with these primitives we can construct an appropriate VRF with adaptive security. Note that some earlier works [7, 22] also achieved such an adaptively secure VRF using unique signatures and random oracles. Here we adopt the approach in Abraham et al. [1], since it removes the random oracle assumption.
We now provide a formal description of how to compile our \(\mathcal {F}_\mathrm{mine}\)-hybrid protocols into real-world protocols using cryptography. The intuition is very simple. Every node commits to a PRF secret key in its public key. This committed secret key is used to evaluate a PRF on \(b = 0\) or \(b=1\) to determine whether the node belongs to the b-th committee. The node can then prove to everyone that the eligibility determination is performed correctly by employing a NIZK. Below we give a more formal description of how to rely on this idea to compile the earlier \(\mathcal {F}_\mathrm{mine}\)-hybrid protocol to the real world.
-
PKI setup. Upfront, a trusted party runs the CRS generation algorithms of the commitment and the NIZK scheme to obtain \({\mathsf{crs}} _\mathrm{comm}\) and \({\mathsf{crs}} _\mathrm{nizk}\). It then chooses a secret PRF key for every node, where the i-th node has key \(\mathsf {sk}_i\). It publishes \(({\mathsf{crs}} _\mathrm{comm}, {\mathsf{crs}} _\mathrm{nizk})\) as the public parameters, and each node i’s public key denoted \(\mathsf {pk}_i\) is computed as a commitment of \(\mathsf {sk}_i\) using a random string \(s_i\). The collection of all users’ public keys is published to form the PKI, i.e., the mapping from each node i to its public key \(\mathsf {pk}_i\) is public information. Further, each node i is given the secret key \((\mathsf {sk}_i, s_i)\).
-
Instantiating
 . Recall that in the ideal-world protocol a node i calls \(\mathcal {F}_\mathrm{mine}{.}{} \mathtt{mine}(b)\) to check if it is in the b-th committee. Now, instead, the node i calls \(\rho := \mathsf{PRF}_{\mathsf {sk}_i}(b)\), and computes the NIZK proof $$\pi := \mathsf{nizk} {.}\mathsf{P}((\rho , \mathsf {pk}_i, {\mathsf{crs}} _\mathrm{comm}, b), (\mathsf {sk}_i, s_i))$$
. Recall that in the ideal-world protocol a node i calls \(\mathcal {F}_\mathrm{mine}{.}{} \mathtt{mine}(b)\) to check if it is in the b-th committee. Now, instead, the node i calls \(\rho := \mathsf{PRF}_{\mathsf {sk}_i}(b)\), and computes the NIZK proof $$\pi := \mathsf{nizk} {.}\mathsf{P}((\rho , \mathsf {pk}_i, {\mathsf{crs}} _\mathrm{comm}, b), (\mathsf {sk}_i, s_i))$$where \(s_i\) the randomness used in committing \(\mathsf {sk}_i\) during the trusted setup. Intuitively, this zero-knowledge proof proves that the evaluation outcome \(\rho \) is correct w.r.t. the node’s public key (which is a commitment of its secret key). The mining attempt for b is considered successful if \(\rho < D_p\) where \(D_p\) is an appropriate difficulty parameter such that a random string of appropriate length is less than \(D_p\) with probability p—the probability p is selected in the same way as the earlier \(\mathcal {F}_\mathrm{mine}\)-hybrid world in Fig. 1. Recall that earlier in our \(\mathcal {F}_\mathrm{mine}\)-hybrid protocol, every message multicast by a so-far honest node i is a vote of the form (b, i) where node i has successfully called \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(b)\). Each such message (b, i) that node i wants to multicast is translated to the real-world protocol as follows: we rewrite (b, i) as \((b, i, \rho , \pi )\) where the terms \(\rho \) and \(\pi \) are those generated by i in place of calling \({\mathcal {F}_\mathrm{mine}} {.}{} \mathtt{mine}(b)\) in the real world (as explained above). Note that in our \(\mathcal {F}_\mathrm{mine}\)-hybrid protocols a node \(j \ne i\) may also relay a message (b, i) mined by i—in the real world, node j would be relaying \((b, i, \rho , \pi )\) instead.
-
Instantiating
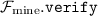 . In the \(\mathcal {F}_\mathrm{mine}\)-hybrid world, a node would call \(\mathcal {F}_\mathrm{mine}{.}{} \mathtt{verify}\) to check the validity of votes upon receiving them, In the real-world protocol, we perform the following instead: upon receiving the vote \((b, i, \rho , \pi )\), a node can verify the vote’s validity by checking:
. In the \(\mathcal {F}_\mathrm{mine}\)-hybrid world, a node would call \(\mathcal {F}_\mathrm{mine}{.}{} \mathtt{verify}\) to check the validity of votes upon receiving them, In the real-world protocol, we perform the following instead: upon receiving the vote \((b, i, \rho , \pi )\), a node can verify the vote’s validity by checking: -
1.
\(\rho < D_p\) where p is an appropriate difficulty parameter parametrized in the same way as Fig. 1 and
-
2.
\(\pi \) is indeed a valid NIZK for the statement formed by the tuple \((\rho , \mathsf {pk}_i, {\mathsf{crs}} _\mathrm{comm}, b)\). The tuple is discarded unless both checks pass.
-
1.
Extending the Security Guarantees to the Real-World Protocol. Now using the same proofs as Abraham et al. [1], we can prove that the compiled real-world protocols enjoy the same security properties as the \(\mathcal {F}_\mathrm{mine}\)-hybrid protocols. Since the proofs follow identically, we omit the details and refer the reader to Abraham et al. [1]. In the following theorem we assume that the pseudorandom function family employed is secure, the non-interactive zero-knowledge proof system employed satisfies computational zero-knowledge and computational soundness, and moreover, the commitment scheme is perfectly binding and computationally hiding.
Theorem 4
(Real-world protocol: restatement of Theorem 1). Assume that the cryptographic primitives employed are secure in the sense mentioned aboveFootnote 5. For parameters \(\epsilon , \delta \in (0, 1)\) which are allowed to be functions in n, the aforementioned real-world protocol terminates in \(O(\log (1/\delta )/\epsilon )\) number of rounds and achieves BA with \(1-\delta - \mathsf{negl}(\kappa )\) probability in the presence of an adversary that adaptively corrupts at most \((1-\epsilon )n\) nodes and runs in time polynomial in \(\kappa \).
Proof
Note our techniques for instantiating \({\mathcal {F}_\mathrm{mine}} \) with actual cryptography are borrowed from Abraham et al. [1]. Their proof for showing that the real-world protocol preserves the security properties proved in the ideal world is immediately applicable to our case.
Notes
- 1.
Here we use a different parameter \(\lambda \) to distinguish from the security parameter \(\kappa \) that is related to the strength of the cryptographic primitives employed.
- 2.
Since in many consensus works the word broadcast is used to mean “Byzantine Agreement”, we use “multicast” rather than “broadcast” to avoid ambiguity.
- 3.
The name \(\mathcal {F}_\mathrm{mine}\) is making an analogy to Bitcoin mining. Each call to \(\mathcal {F}_\mathrm{mine}\) is like an attempt to mine a ticket to vote in the protocol.
- 4.
We need either the subgroup decision assumption or the decisional linear assumption according to Groth et al. [17].
- 5.
Specifically, see the “Cryptographic building blocks” paragraph above for the required security notions of the cryptographic primitives employed.
References
Abraham, I., et al.: Communication complexity of Byzantine agreement, revisited. In: PODC (2019)
Abraham, I., Devadas, S., Dolev, D., Nayak, K., Ren, L.: Synchronous Byzantine agreement with optimal resilience, expected \(o(n^2)\) communication, and expected \(o(1)\) rounds. In: Financial Cryptography and Data Security (FC) (2019)
Boyle, E., Chung, K.-M., Pass, R.: Large-scale secure computation: multi-party computation for (parallel) RAM programs. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 742–762. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_36
Braud-Santoni, N., Guerraoui, R., Huc, F.: Fast Byzantine agreement. In: ACM Symposium on Principles of Distributed Computing, PODC 2013, Montreal, QC, Canada, 22–24 July 2013, pp. 57–64 (2013)
Hubert Chan, T.-H., Pass, R., Shi, E.: Consensus through herding. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11476, pp. 720–749. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_24
Hubert Chan, T.-H., Pass, R., Shi, E.: Sublinear-round Byzantine agreement under corrupt majority (2019). Online full version of this paper. https://eprint.iacr.org/2019/886
Chen, J., Micali, S.: ALGORAND: the efficient and democratic ledger (2016). https://arxiv.org/abs/1607.01341
Chor, B., Merritt, M., Shmoys, D.B.: Simple constant-time consensus protocols in realistic failure models. J. ACM 36(3), 591–614 (1989)
Cohen, R., Coretti, S., Garay, J., Zikas, V.: Probabilistic termination and composability of cryptographic protocols. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 240–269. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_9
Cohen, R., Haitner, I., Makriyannis, N., Orland, M., Samorodnitsky, A.: On the round complexity of randomized Byzantine agreement. In: 33rd International Symposium on Distributed Computing, DISC 2019, Budapest, Hungary, 14–18 October 2019, pp. 12:1–12:17 (2019)
Dolev, D., Strong, H.R.: Authenticated algorithms for Byzantine agreement. SIAM J. Comput. SIAM COMP 12(4), 656–666 (1983)
Feldman, P., Micali, S.: An optimal probabilistic protocol for synchronous Byzantine agreement. SIAM J. Comput. 26(4), 873–933 (1997)
Fitzi, M., Nielsen, J.B.: On the number of synchronous rounds sufficient for authenticated Byzantine agreement. In: Keidar, I. (ed.) DISC 2009. LNCS, vol. 5805, pp. 449–463. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04355-0_46
Garay, J., Katz, J., Koo, C.-Y., Ostrovsky, R.: Round complexity of authenticated broadcast with a dishonest majority. In: 48th Annual IEEE Symposium on Foundations of Computer Science (FOCS), November 2007
Garay, J.A., Katz, J., Kumaresan, R., Zhou, H.-S.: Adaptively secure broadcast, revisited. In: Proceedings of the 30th Annual ACM SIGACT-SIGOPS Symposium on Principles of Distributed Computing, PODC 2011, pp. 179–186. ACM, New York (2011)
Goldwasser, S., Pavlov, E., Vaikuntanathan, V.: Fault-tolerant distributed computing in full-information networks. In: Proceedings of the 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS 2006), Berkeley, California, USA, 21–24 October 2006, pp. 15–26 (2006)
Groth, J., Ostrovsky, R., Sahai, A.: New techniques for noninteractive zero-knowledge. J. ACM 59(3), 11:1–11:35 (2012)
Hirt, M., Zikas, V.: Adaptively secure broadcast. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 466–485. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_24
Kapron, B.M., Kempe, D., King, V., Saia, J., Sanwalani, V.: Fast asynchronous Byzantine agreement and leader election with full information. ACM Trans. Algorithms 6(4), 68:1–68:28 (2010)
Karlin, A., Yao, A.C.-C.: Probabilistic lower bounds for byzantine agreement. Manuscript (1986)
Katz, J., Koo, C.-Y.: On expected constant-round protocols for Byzantine agreement. J. Comput. Syst. Sci. 75(2), 91–112 (2009)
Kiayias, A., Russell, A., David, B., Oliynykov, R.: Ouroboros: a provably secure proof-of-stake blockchain protocol. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 357–388. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_12
King, V., Saia, J.: Breaking the \(O(N^2)\) bit barrier: scalable Byzantine agreement with an adaptive adversary. J. ACM 58(4), 18:1–18:24 (2011)
King, V., Saia, J., Sanwalani, V., Vee, E.: Scalable leader election. In: SODA (2006)
Lamport, L., Shostak, R., Pease, M.: The Byzantine generals problem. ACM Trans. Program. Lang. Syst. 4(3), 382–401 (1982)
Acknowledgments
We would like to thank Vassilis Zikas for very helpful discussions, and we gratefully thank the PKC’2020 reviewers for the detailed and thoughtful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Chan, TH.H., Pass, R., Shi, E. (2020). Sublinear-Round Byzantine Agreement Under Corrupt Majority. In: Kiayias, A., Kohlweiss, M., Wallden, P., Zikas, V. (eds) Public-Key Cryptography – PKC 2020. PKC 2020. Lecture Notes in Computer Science(), vol 12111. Springer, Cham. https://doi.org/10.1007/978-3-030-45388-6_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-45388-6_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45387-9
Online ISBN: 978-3-030-45388-6
eBook Packages: Computer ScienceComputer Science (R0)




 -Hybrid Protocol
-Hybrid Protocol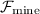 for Random Eligibility Determination
for Random Eligibility Determination
 -Hybrid World
-Hybrid World -Hybrid World
-Hybrid World
 with Cryptography
with Cryptography . Recall that in the ideal-world protocol a node i calls
. Recall that in the ideal-world protocol a node i calls 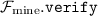 . In the
. In the 