Keywords

1 Introduction

In recent years, it has become popular to create interior goods and decorations by hand. wire art is one of handicraft. Wire art is an art formed by bending according to the design drawings designed using aluminum wire. This art is attractive molding goods because it is low cost and easy to get by mail order. However, a high technique is necessary for producing 3D wire art, and it is often produced by the hand of an expert and the craftsman.

In this paper, we propose a method of automatically determining the wire art curve shape along the shape of the 3D model. Moreover, the wire art curve shape is determined from several evaluation index. In our method, we define multiple infinite planes from an oriented bounding box and Gaussian Curvature of the input 3D model. After that, the intersection line between the polygon mesh of the 3D model and the infinite plane is calculated, and the curve of the wire art is automatically determined based on the evaluation index of length and complexity. By showing a set of 3D contour curves from the input 3D model, automatic design of wire art with maintaining the shape feature of the 3D model is realized. We apply the proposed method to various 3D models and verify the effectiveness of the proposed evaluation index.

2 Related Works

Digital Design Method.

In recent years, there are many tools to support materials and production methods using computers in hand-made fabrics and handicrafts that can be produced by hand. In the support tool, it is possible to produce original handicrafts by using CAD system etc. Therefore, the demand for design support systems for simulating designs and deliverables is increasing.

Design Aid of Wire Art.

As a study to aid the design of wire art, there is a study that present feasible wire art from 2D line drawing by Iarussi et al. [1]. In addition, there is a study that automatically fabricated 3D wire art using a wire bending machine from 3D model and its contours by Miguel et al. [2]. In this study, they calculate the curves that can be fabricated by wire bending machines. However, due to the limitations of the wire bending machine, it is not possible to express complex contours. In our method, it is possible to express a complex contour from the intersection of the plane and the 3D model, and automatic design of the wire art curve which maintains the shape characteristics of the 3D model is performed.

3 Proposed Method

3.1 Overview

In the proposed method, the polygon mesh of the 3D model and the accuracy of the output are input. First, we calculate the OBB of the input model and the Gaussian curvature of each vertex. Next, a plane for each xyz axis is generated at the vertex position where the Gaussian curvature is the largest. This plane has a slope along the direction of OBB. Moreover, we generate planes symmetrically from the generated plane according to the accuracy of the output. Then, the wire art curve of the output is determined by calculating the cross-sectional line between the generated plane and the polygon mesh of the input model and evaluating its group. (see Fig. 1).

Fig. 1.
figure 1

Given a 3D model (a), our system calculates OBB and Gaussian curvature (b) and generates a reference plane (c). Moreover, generate a plane evenly based on a reference plane (d) and determine the wire art curve by the evaluation value (e). The result of combining the wire art curves for each xyz axis is the final output (f).

Full size image

3.2 Oriented Bounding Box

In this method, the wire art curve is determined using the curve along the input model. Therefore, it is necessary to calculate OBB of the input model. we calculate OBB, it is possible to enclose the model in as small a square as possible, regardless of which direction the model is facing. OBB can be calculated by using principal component analysis for the model. According to principal component analysis, the orientation and length of each xyz axis can be obtained by treating the scattering of each vertex of the model as a variance covariance matrix.

3.3 Gaussian Curvature

In this method, the reference position of the wire art is determined by the curvature of the model. Therefore, it is necessary to calculate the Gaussian curvature of the input model. We confirm the curvature of the mesh by calculating the Gaussian curvature. The Gaussian curvature is calculated from each vertex of the input model. In addition, when the absolute value of Gaussian curvature is large, the unevenness of the mesh becomes remarkable. Therefore, the reference position of the wire art is the vertex position where the absolute value of the Gaussian curvature is the largest. We calculate Gaussian curvature by Meyer et al. [3].

3.4 Reference Plane

We generate three planes at the reference position determined in Sect. 3.3. In addition, this plane has normal direction for each axis of the OBB. We generate planes worth the number of output precisions on the left and right of the three generated planes. This output precision is 30.

3.5 Cross-Sectional Line

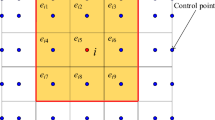
We calculate the cross-sectional line. The cross-sectional line is a line segment where the mesh of the input model and the plane of each xyz axis generated in Sect. 3.4 intersect. The intersection is calculated as:

$$ X = A + \overrightarrow {AB} \left( {\frac{{\left| {PA \cdot N} \right|}}{{\left( {\left| {PA \cdot N} \right| + \left| {PB \cdot N} \right|} \right)}}} \right) $$
(1)

Where, X is the intersection of the plane and the line of the mesh, AB is the line of the mesh, P is the point on the plane, and N is the normal of the plane. (see Fig. 2).

Fig. 2.
figure 2

Cross-Sectional line group calculated for plane of each xyz axis.

Full size image

3.6 Layout-Wire

We use the cross-sectional line group calculated in Sect. 3.5 as wire art curve candidates and determine the wire art curve to be output based on the evaluation value. However, the cross-sectional line with the reference plane is determined as a wire art curve, regardless of the evaluation value. The evaluation value is the sum of the circularity and the normalized perimeter of the cross-sectional line. This evaluation value is calculated for the calculated cross-sectional line group. The evaluation value is calculated as:

$$ E(l) = E_{circularity} (l) + E_{contour} (l) $$
(2)

In addition, the circularity is calculated as:

$$ E_{circularity} (l) = \frac{4\pi S}{{l_{length} }} $$
(3)

Moreover, the normalized perimeter of the cross-sectional line is calculated as:

$$ E_{contour} (l) = \frac{{l_{length} }}{{Max_{length} }} $$
(4)

Then, the wire art curve determines the number of 30% of the cross-sectional line group in the order in which the evaluation value is high. However, the cross-sectional line with a high evaluation value may be concentrated. When concentrated, the wire art curve has biased. Therefore, the cross-sectional line adjacent to the determined cross-sectional line is not selected.

4 Experimental Result

We calculated several wire art curves using this method. (see Fig. 3). The following describes the results in detail.

Fig. 3.
figure 3

Determined the wire art curve. From left to right: input model, reference plane, the wire art curve.

Full size image

We consider that the shape characteristics of the input model can be reflected by using circularity and normalized perimeter as evaluation values. In addition, we consider that the balance of the wire art curve is maintained by using the reference plane as the position where the unevenness of the input model is remarkable.

However, if the input model is a complex object, the curve is not determined in the part shown in Fig. 4. In this method, the cross-sectional line of the wide area of the model is determined by the evaluation index. Due to the local area of the model is not considered. Therefore, it is necessary to segment mesh the input model and disassemble wide-area parts and local parts [4].

Fig. 4.
figure 4

Problematic the wire art curve. From left to right: input model, reference plane, the wire art curve. There is no wire art curve in the area surrounded by the red rectangle.

Full size image

5 Conclusion and Future Work

We proposed a system to assist in the design of the wire art curve with 3D models and output accuracy input. The shape characteristics of the input model were captured from orientation and curvature. In addition, the wire art curve which maintained the shape feature by the evaluation values of the cross-sectional line group between the plane and the mesh was determined.

For future work, to disassemble 3D model in order to be able to calculate the shape characteristics of local areas of the 3D model. At the present, it does not consider the support when assembling from the decided wire art curve. Therefore, we consider that support the assembly procedure through animation and viewer.