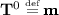Abstract
This paper proposes a decentralized netting protocol that guarantees the privacy of the participants. Namely, it leverages the blockchain and its security properties to relax the trust assumptions and get rid of trusted central parties. We prove the protocol to be optimal and we analyze its performance using a proof-of-concept implemented on top of Hyperledger Fabric.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
These attacks send a payment instruction to change account balances while netting is taking place to invalidate the range proofs computed prior to the update.
References
Furgal, A., Garratt, R., Guo, Z., Hudson, D.: A proposal for a decentralized liquidity savings mechanism with side payments. R3 Report 2018
Bitcoin: A Peer-to-Peer Electronic Cash System. https://bitcoin.org/bitcoin.pdf
Chapman, J., Garratt, R., Hendry, S., MacCormack, A., McMahon, W.: Project Jasper: are distributed wholesale payment systems feasible yet. https://www.bankofcanada.ca/wp-content/uploads/2017/05/fsr-june-2017-chapman.pdf
Project Ubin Phase 2. https://www.mas.gov.sg/schemes-and-initiatives/Project-Ubin
Bech, M., Soramäki, K.: Gridlock resolution in interbank payment systems. Discussion Paper 9/2001, Bank of Finland
Güntzer, M., Jungnickel, D., Leclerc, M.: Efficient algorithms for the clearing of interbank payments. Eur. J. Oper. Res. 106(1), 212–219 (1998)
Shafransky, Y., Doudkin, A.: An optimization algorithm for the clearing of interbank payments. Eur. J. Oper. Res. 171(3), 743–749 (2006)
Wang, X., Xu, X., Feagan, L., Huang, S., Jiao, L., Zhao, W.: Inter-bank payment system on enterprise blockchain platform. In: IEEE CLOUD 2018 Cloud and Blockchain Workshop (2018)
Narula, N., Vasquez, W., Virza, M.: zkLedger: privacy-preserving auditing for distributed ledgers. In: 15th USENIX Symposium on Networked Systems Design and Implementation (NSDI 2018). USENIX Association (2018)
Poelstra, A., Back, A., Friedenbach, M., Maxwell, G., Wuille, P.: Confidential assets. In: Financial Cryptography Bitcoin Workshop. https://blockstream.com/bitcoin17-final41.pdf
Pedersen, T.P.: Non-interactive and information-theoretic secure verifiable secret sharing. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 129–140. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_9
Camenisch, J., Chaabouni, R., Shelat, A.: Efficient protocols for set membership and range proofs. In: Pieprzyk, J. (ed.) ASIACRYPT 2008. LNCS, vol. 5350, pp. 234–252. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89255-7_15
Bunz, B., Bootle, J., Boneh, D., Peolstra, A., Wuille, P., Maxwell, G.: Bulletproofs: short proofs for confidential transactions and more. In: 2018 IEEE Symposium on Security and Privacy (SP). IEEE (2018)
Hyperledger Fabric 1.2. https://hyperledger-fabric.readthedocs.io/en/release-1.2/whatis.html
Blockchain based payment system and netting protocol implementation. http://github.com/blockchain-research/gridlock
Borromean Ring signature based zero-knowledge range proof implementation. http://github.com/blockchain-research/crypto
Package btcec implements support for the elliptic curves needed for Bitcoin, July 2017. https://godoc.org/github.com/btcsuite/btcd/btcec
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Proof of Optimality
We first prove for \(f_i=T_i(\mathbf {x})\), then we show the result is invariant to the choice of \(f_i\). Without loss of generality, we also assume \(d_i=0, \forall i\) to simplify proof notation. Let \(\mathbf {m} = [m_1^{}, m_2^{}, \dots , m_n^{}]^\top \) and \(\mathbf {T} = [T_1^{}, T_2^{}, \dots , T_n^{}]^\top \in \mathbb {R}^n\). The problem defined by Eqs. (7) to (12) can be rewritten as



where \(\mathbf {0} \le \mathbf {T} \le \mathbf {m}\) stands for \(0 \le T_i \le m_i, \forall 1 \le i \le n\). Note that the definitions of \(S_i(T_i^{})\) and \(R_i(\mathbf {T})\) above implicitly model the constraints defined in (12) for each participant i. In other words, if there are \(T_i^{}\) payments settled for participant i, \(S_i(T_i^{})\) imply that they must be the first \(T_i^{}\) payments in \(\mathcal {Q}_i\). Let \(\mathbf {T}^t\) denote the value of \(\mathbf {T}\) at the tth iteration of Algorithm 1. In addition, \(\mathbf {T}^0\) is set to \(\mathbf {m}\) for initialization. Then Algorithm 1 essentially becomes
-
Initialization:
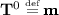
-
Repeat following steps
-
Calculate \(R_i(\mathbf {T}^t), \forall i \in [n]\)
-
\(\forall i \in [n]\) find
$$\begin{aligned} T_i^{t+1} = \text {argmax}_{T} \Big \{ T \in [m_i]\Big \} \end{aligned}$$(21)$$\begin{aligned} \text {such that} \nonumber \\ \hat{B}_i - S_i(T_i^{t+1}) + R_i(\mathbf {T}^t) \ge 0 \end{aligned}$$(22)$$\begin{aligned} x_{i,k+1}\le x_{i,k}, \forall k\in [m_i^{}-1] \end{aligned}$$(23) -
If \(\mathbf {T}^{t+1} = \mathbf {T}^t\), stop. Otherwise, continue the loop.
-
The decentralized netting protocol is guaranteed to find the optimal solution. To prove this, we first prove that line 6–12 in Algorithm 1 is equivalent to Eqs. 21–23 above.
By the exit condition, we have \(\tilde{B}^{t+1}_i \ge 0\). Therefore we could construct the following case, where
Suppose there exists another optimal solution \(\mathcal {T}_i > T_i^{t+1}\) and
Since
it implies that
Equation 27 clearly violates the non-overdraft condition. Therefore such \(\mathcal {T}\) does not exist and \(T_i^{t+1}\) is the maximum value that can be achieved at \(t+1\)th iteration. Furthermore, we have
In view of line 12 in Algorithm 1, the above two equations imply that
We note that the decentralized netting protocol starts with all the payment in queue and removes current invalid payments for each deficient participant. The optimality of \(T_i\) at each iteration plus the monotonicity of \(T_i\) over iterations guarantee that the first feasible solution will also be the optimal solution and it is unique.
Next, we show its invariance. If there is only one feasible solution, then it also achieves the maximum total value and number of payments. If there are two or more feasible solutions, the monotone decreasing of \(T_i\) imply that any other feasible solution after the first one contains same or fewer payments for each participant and thus less value. This completes the proof.
B Functions of the Smart Contract
In Table 2, we describe the detailed functions of our implemented smart contract.
Rights and permissions
Copyright information
© 2020 International Financial Cryptography Association
About this paper
Cite this paper
Cao, S., Yuan, Y., De Caro, A., Nandakumar, K., Elkhiyaoui, K., Hu, Y. (2020). Decentralized Privacy-Preserving Netting Protocol on Blockchain for Payment Systems. In: Bonneau, J., Heninger, N. (eds) Financial Cryptography and Data Security. FC 2020. Lecture Notes in Computer Science(), vol 12059. Springer, Cham. https://doi.org/10.1007/978-3-030-51280-4_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-51280-4_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51279-8
Online ISBN: 978-3-030-51280-4
eBook Packages: Computer ScienceComputer Science (R0)