Abstract
In this work, we propose a Transformer-based model to trace students’ knowledge acquisition. We modified the Transformer structure to utilize 1) the association between questions and skills and 2) the elapsed time between question steps. The use of question-skill associations allows the model to learn specific representation for frequently encountered questions while representing rare questions with their underline skill representations. The inclusion of elapsed time opens the opportunity to address forgetting. Our approach outperforms the state-of-the-art methods in the literature by roughly 10% in AUC with frequently used public datasets.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Bayesian Knowledge Tracing (BKT) is an established approach to modeling skill acquisition of students working with intelligent tutoring systems. However, BKT is far from an ideal solution, and multiple improvements and extensions were suggested to it over the years. One of such extensions is Deep Knowledge Tracing (DKT). The first DKT [6] adopted the Recurrent Neural Network (RNN) architecture from the deep learning community. Recent publications on DKT discuss various RNN architecture modifications to adapt to student learning theories as well as explore new deep learning models. Our work is inspired by both and proposes to use the Transformer architecture to model students’ knowledge state.
The Transformer model was first proposed by the Google Brain team [9] to generate better neural translations. It soon became the dominant model in many Natural Language Processing (NLP) problems [2, 7]. The main advantage of the Transformer over RNN is its ability to learn long-range dependencies [2].
We modified the Transformer architecture so that it does not directly learn the representation of each question. Instead, it learns the representation of the underlying W-matrix that relates knowledge components to question items, including the cases when multiple knowledge components are associated with an item. This modification allows the model to learn specific representation for frequently encountered questions while represent rare questions with their underline skill representations. Further, we allow the attention weight between question items to decay as students work on questions or problems, which effectively represents forgetting.
2 Related Work
The original Deep Knowledge Tracing (DKT) Model [6] used an RNN based architecture and claimed to outperform BKT by a large margin. However, latter works [3, 10] showed that RNN based DKT is not superior than BKT models over a pool of datasets when data preprocessing errors are taken into account.
Recent work on DKT follows two general patterns. First, a group of studies [4, 11] tried to adjust the RNN structure so that it is consistent with the students’ learning process. For example, the Dynamic Key-Value Memory Networks [11] explicitly maintained knowledge components and knowledge states. Further, Nagatan and colleagues [4] intentionally modeled students’ forgetting behavior in RNN but achieved only limited success.
Another group of DKT papers seeks to leverage recently developed Transformer models [1, 5, 8]. Pandey and Karypis [5] used a self-attention model which is a simplified version of the Transformer. Ralla and colleagues [8] used Transformer Encoder to pre-train students’ interactions. Choi et al. [1] experimented with different alternatives to rewiring the components in the original Transformer. All these works showed inspiring results and motivated this study.
3 Methods
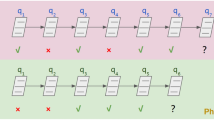
Figure 1 represents a simplified version of our adapted Transformer model. The main inputs to our adapted Transformer model is a sequence tuples \(x_i = (q_i, c_i)\), and timestamp \(t_i\). Here, \(q_i\) represents the question item a student is trying to answer, and \(c_i \in {0, 1}\) represents whether the response is correct. The goal of the model is a sequence of correctness estimates, \(c_{i+1}\), representing whether a student correctly solved the next question \({q_{i+1}}\). Formally, the Transformer model is trying to predict \(P(c_{i+1} = 1 | x_0, .., x_i, t_0, ..., t_i, q_{i + 1})\).
Interaction Embedding Layer. A student interaction, \(x_i\), will be first encoded as an index, \(d_i\), and passed to the interaction mapping layer:
\(e_i\) is the vector representation of a student interaction \(x_i\). \(W_{d_i.}\) represents the weights associated with all latent skills for \(d_i\). Each column of S is a vector representation of a latent skill. So, \(e_i\) is a weighted sum of all underlying latent skills.
Transformer Block – Masked Attention. The outputs of Interaction Embedding Layer, \(e_i\), is directly passed to a Transformer Block:
the masked attention layer first extracts query \(q_i\), key \(k_i\), and value \(v_i\) from the inputs \(e_i\). It then assign an attention, \(A_{ij}\), to a past interaction \(e_j\) based on two components: 1) \(q_ik_j\), the query-key agreement between \(e_i\) and \(e_j\), which could be interpreted as the degree of latent skills overlapping between interaction \(e_i\) and \(e_j\); 2) A time gap bias, \(b(\varDelta t_{i-j})\), which adjusts the attention weight by the time gap between interactions \(e_i\) and \(e_j\). The hidden representation \(h_i\) is a weighted sum of the past value representations of \(e_j\). A Transformer block also have feedforward layer, normalization layer, and residual connections. We recommend readers to read the original paper [9] for more detail.
Linear Layer + Loss. The outputs of a stack of Transformer blocks is feed to the linear layer before calculating the final loss. \(e_{i+1}\) and \(e^*_{i+1}\) are the results of applying Interaction Mapping Layer to \((q_{i + 1}, 1)\) and \((q_{i + 1}, 0)\).
4 Experiments
We ran 5-fold student-stratified cross-validation on three datasets that are frequently used in the literature. Table 1 lists descriptive statistics for the datasets.
ASSISTments2017Footnote 1. Data from the ASSISTment online tutoring system.
STAT F2011Footnote 2. This data is from a college-level engineering statics course.
KDD, AFootnote 3. This data is the challenge set A – Algebra I 2008–2009 data set from the KDD 2010 Educational Data Mining Challenge.
5 Results and Discussion
Table 1 summarizes our findings and compares them to the start-of-the-art Deep Knowledge Tracing model results in the literature, as well as the Bayesian Knowledge Tracing (BKT) model. Our adapted Transformer model is superior to BKT on all datasets and outperforms the state-of-the-art DKT models from the literature by 9.81% and 11.02% on ASSISTments 2017 and STAT F2011 datasets. The remarkable gain is not due to the structure of the original transformer model. Pandey and Karypis [5]’s self-attention model is roughly equivalent to a 1-layer Transformer. Their reported AUC score on ASSISTments 2017 and STAT F2011 is about 10% worse than our adapted Transformer.
To further illustrate this point, we repeat the experiment on the original Transformer with/without the modified components, as illustrated in Table 2. The original Transformer gains an obvious performance boost by adding the interaction skill mapping and time-bias to its structure.
To conclude, our adapted Transformer architecture generated promising results on frequently used public datasets. For future work, we intend to explore how to efficiently incorporate more feature information into the Transformer architecture, as well as how to represent hierarchical relations between skills in the interaction embedding layer.
References
Choi, Y., et al.: Towards an appropriate query, key, and value computation for knowledge tracing. arXiv preprint arXiv:2002.07033 (2020)
Devlin, J., Chang, M.W., Lee, K., Toutanova, K.: Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805 (2018)
Khajah, M., Lindsey, R.V., Mozer, M.C.: How deep is knowledge tracing? In: Proceedings of the 9th International Conference on Educational Data Mining, EDM 2016, pp. 94–101 (2016)
Nagatani, K., Chen, Y.Y., Zhang, Q., Chen, F., Sato, M., Ohkuma, T.: Augmenting knowledge tracing by considering forgetting behavior. In: The Web Conference 2019 - Proceedings of the World Wide Web Conference, WWW 2019, pp. 3101–3107 (2019). https://doi.org/10.1145/3308558.3313565
Pandey, S., Karypis, G.: A self-attentive model for knowledge tracing. arXiv preprint arXiv:1907.06837 (2019)
Piech, C., et al.: Deep knowledge tracing. In: Advances in Neural Information Processing Systems, pp. 505–513 (2015)
Radford, A., Wu, J., Child, R., Luan, D., Amodei, D., Sutskever, I.: Language models are unsupervised multitask learners. OpenAI Blog 1(8), 9 (2019)
Ralla, A., Siddiqie, S., Krishna Reddy, P., Mondal, A.: Assessment modeling: fundamental pre-training tasks for interactive educational systems youngduck. In: ACM International Conference Proceeding Series, pp. 209–213 (2020). https://doi.org/10.1145/1122445.1122456
Vaswani, A., et al.: Attention is all you need. In: Advances in Neural Information Processing Systems, pp. 5998–6008 (2017)
Xiong, X., Zhao, S., Van Inwegen, E.G., Beck, J.E.: Going deeper with deep knowledge tracing. In: International Educational Data Mining Society (2016)
Zhang, J., Shi, X., King, I., Yeung, D.Y.: Dynamic key-value memory networks for knowledge tracing. In: 26th International World Wide Web Conference, WWW 2017, pp. 765–774 (2017). https://doi.org/10.1145/3038912.3052580
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Pu, S., Yudelson, M., Ou, L., Huang, Y. (2020). Deep Knowledge Tracing with Transformers. In: Bittencourt, I., Cukurova, M., Muldner, K., Luckin, R., Millán, E. (eds) Artificial Intelligence in Education. AIED 2020. Lecture Notes in Computer Science(), vol 12164. Springer, Cham. https://doi.org/10.1007/978-3-030-52240-7_46
Download citation
DOI: https://doi.org/10.1007/978-3-030-52240-7_46
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-52239-1
Online ISBN: 978-3-030-52240-7
eBook Packages: Computer ScienceComputer Science (R0)