Abstract
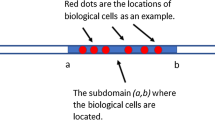
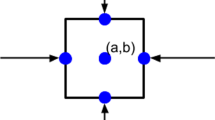
We consider a cell-based approach in which the balance of momentum is used to predict the impact of cellular forces on the surrounding tissue. To this extent, the elasticity equation and Dirac Delta distributions are combined. In order to avoid the singularity caused by Dirac Delta distribution, alternative approaches are developed and a Gaussian distribution is used as a smoothed approach. Based on the application that the pulling force is pointing inward the cell, the smoothed particle approach is probed as well. In one dimension, it turns out that the aforementioned three approaches are consistent. For two dimensions, we report a computational consistence between the direct and smoothed particle approach.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
S. Enoch and D. J. Leaper. Basic science of wound healing. Surgery (Oxford), 26 (2): 31–37, 2008.
D. Koppenol. Biomedical implications from mathematical models for the simulation of dermal wound healing. 2017.
B. Laud. Electromagnetics. New Age International, 1987.
Q. Peng and F. Vermolen, Point Forces and Their Alternatives in Cell-Based Models for Skin Contraction. Reports of the Delft Institute of Applied Mathematics, vol. 19-03, Delft University, the Netherlands, 2019. ISSN: 1389-6520
Acknowledgements
The authors appreciate China Scholarship Council (CSC) for the financial support on this project.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Peng, Q., Vermolen, F. (2021). Point Forces and Their Alternatives in Cell-Based Models for Skin Contraction. In: Vermolen, F.J., Vuik, C. (eds) Numerical Mathematics and Advanced Applications ENUMATH 2019. Lecture Notes in Computational Science and Engineering, vol 139. Springer, Cham. https://doi.org/10.1007/978-3-030-55874-1_75
Download citation
DOI: https://doi.org/10.1007/978-3-030-55874-1_75
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-55873-4
Online ISBN: 978-3-030-55874-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)