Abstract
Succinct non-interactive arguments (SNARGs) enable proofs of \(\mathsf {NP} \) statements with very low communication. Recently, there has been significant work in both theory and practice on constructing SNARGs with very short proofs. Currently, the state-of-the-art in succinctness is due to Groth (Eurocrypt 2016) who constructed a SNARG from bilinear maps where the proof consists of just 3 group elements.
In this work, we first construct a concretely-efficient designated-verifier (preprocessing) SNARG with inverse polynomial soundness, where the proof consists of just 2 group elements in a standard (generic) group. This leads to a 50% reduction in concrete proof size compared to Groth’s construction. We follow the approach of Bitansky et al. (TCC 2013) who describe a compiler from linear PCPs to SNARGs in the preprocessing model. Our improvement is based on a new linear PCP packing technique that allows us to construct 1-query linear PCPs which can then be compiled into a SNARG (using ElGamal encryption over a generic group). An appealing feature of our new SNARG is that the verifier can precompute a statement-independent lookup table in an offline phase; verifying proofs then only requires 2 exponentiations and a single table lookup. This makes our new designated-verifier SNARG appealing in settings that demand fast verification and minimal communication.
We then turn to the question of constructing arguments where the proof consists of a single group element. Here, we first show that any (possibly interactive) argument for a language \(\mathcal {L}\) where the verification algorithm is “generic” (i.e., only performs generic group operations) and the proof consists of a single group element, implies a witness encryption scheme for \(\mathcal {L}\). We then show that under a yet-unproven, but highly plausible, hypothesis on the hardness of approximating the minimal distance of linear codes, we can construct a 2-message laconic argument for \(\mathsf {NP} \) where the proof consists of a single group element. Under the same hypothesis, we obtain a witness encryption scheme for \(\mathsf {NP} \) in the generic group model. Along the way, we show that under a conceptually-similar but proven hardness of approximation result, there is a 2-message laconic argument for \(\mathsf {NP} \) with negligible soundness error where the prover’s message consists of just 2 group elements. In both settings, we obtain laconic arguments (and linear PCPs) with linear decision procedures. Our constructions circumvent a previous lower bound by Groth on such argument systems with linear decision procedures by relying on imperfect completeness. Namely, our constructions have vanishing but not negligible completeness error, while the lower bound of Groth implicitly assumes negligible completeness error of the underlying argument. Our techniques thus highlight new avenues for designing linear PCPs, succinct arguments, and witness encryption schemes.
O. Barta—Supported by ERC Project NTSC (742754).
Y. Ishai—Supported by ERC Project NTSC (742754), NSF-BSF grant 2015782, BSF grant 2018393, and a joint Israel-India grant. Part of this work was done while visiting the Simons Institute for the Theory of Computing.
R. Ostrovsky—Supported in part by DARPA under Cooperative Agreement No. HR0011-20-2-0025, NSF-BSF Grant 1619348, US-Israel BSF grant 2012366, Google Faculty Award, JP Morgan Faculty Award, IBM Faculty Research Award, Xerox Faculty Research Award, OKAWA Foundation Research Award, B. John Garrick Foundation Award, Teradata Research Award, and Lockheed-Martin Corporation Research Award. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of DARPA, the Department of Defense, or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for governmental purposes not withstanding any copyright annotation therein.
D. J. Wu—Supported by NSF CNS-1917414 and a University of Virginia SEAS Research Innovation Award. Part of this work was done while visiting the Simons Institute for the Theory of Computing.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Interactive proof systems [GMR85] provide a general framework that allows a verifier to efficiently check claims made by a (possibly malicious) prover. The two properties we require from an interactive proof system are completeness, which says that an honest prover should successfully convince an honest verifier of a true statement, and soundness, which says that a malicious prover should not be able to convince an honest verifier of a false statement, except perhaps with small probability.
An important metric in the design of interactive proof systems is the communication complexity, and specifically, the amount of communication from the prover to the verifier. For an \(\mathsf {NP} \) language, an interactive proof system is said to be laconic or succinct if the total communication from the prover to the verifier is sublinear in the size of the \(\mathsf {NP} \) witness. In the setting of general \(\mathsf {NP} \) languages, non-trivial savings in the prover-to-verifier communication (beyond sending the classic \(\mathsf {NP} \) witness) are unlikely if we require the proof system to be statistically sound (i.e., sound even against an unbounded prover) [BHZ87, GH98, GVW01, Wee05]. If we relax the requirements and only consider proof systems with computational soundness (known as “argument systems” [BCC88]), significant efficiency improvements are possible. Starting from the seminal work of Kilian [Kil92] who gave the first construction of an interactive laconic argument from probabilistically checkable proofs (PCPs) and collision-resistant hash functions, a long sequence of works have constructed interactive laconic arguments and succinct non-interactive arguments (“SNARGs” [GW11]) for general \(\mathsf {NP} \) languages where the communication is polylogarithmic in the size of the classic \(\mathsf {NP} \) witness (cf. [Mic00, Mie08, CL08, Gro10, BCCT12, Lip12, BC12, GGPR13, BCI+13, DFGK14, Gro16, BCC+16, BCC+17, BISW17, BBB+18, BISW18, BBHR19] and the references therein).
Minimizing proof size. A long sequence of works, beginning with Groth’s construction of a succinct argument with a constant number of bilinear group elements [Gro10], has sought to minimize the proof size in SNARGs for \(\mathsf {NP} \). Groth’s initial construction had proofs with 42 group elements; this was later reduced to 39 elements by Lipmaa [Lip12]. In both constructions, the prover complexity was quadratic in the size of the \(\mathsf {NP} \) verification circuit. Subsequently, using a new characterization of \(\mathsf {NP} \) based on quadratic span programs, Gennaro et al. [GGPR13] showed how to construct SNARGs where the proof consists of just 7 group elements and where the prover computation is quasi-linear in the size of the verification circuit. Bitansky et al. [BCI+13] introduced a more abstract view of quadratic span programs as implying a “linear PCP,” where a verifier can make a small number of inner product queries to a proof vector, and described a general compiler from linear PCPs to SNARGs using a notion called linear-only encryption. A similar compiler was implicit in [GGPR13], and both of these works follow the high-level blueprint introduced in [IKO07, Gro10]. Danezis et al. [DFGK14] subsequently refined quadratic span programs to square span programs and showed how to construct succinct arguments with just 4 group elements. This line of work culminated with [Gro16], which showed how to construct succinct arguments with just 3 group elements and with very efficient verification. These advances in constructing highly succinct arguments with lightweight verification have served as the basis for a number of efficient implementations [PHGR13, BCG+13, BCG+14, BBFR15]. The work of Groth [Gro16] raises the following natural question on the possibility of even shorter proofs:
Bitansky et al. [BCI+13] previously showed that by instantiating their compiler with a linear PCP built from classic PCPs (e.g., [ALM+98]) and with the ElGamal encryption scheme [ElG84], one can obtain a designated-verifier SNARG in which the proof consists of just two group elements. (Note that in the designated-verifier setting, the verifier possesses a secret key that it uses to check proofs [KMO89].) A limitation of the construction from [BCI+13] is the inherent reliance on “classic” PCPs, where the verifier is restricted to read individual symbols of the proof instead of the inner-product queries of a linear PCP. This greatly reduces the concrete efficiency of the resulting construction in comparison to alternative pairing-based constructions and implementations.
This work. In this work, we develop new techniques for constructing designated-verifier SNARGsFootnote 1 (and laconic arguments) where the proof size consists of just two group elements. In particular, we provide the following new constructions:
-
Concretely-efficient SNARGs with 2 group elements: We introduce a new “packing” technique for constructing 1-query linear PCPs from k-query linear PCPs. We then apply the compiler from [BCI+13], in conjunction with ElGamal encryption,Footnote 2 to obtain a designated-verifier SNARG where the proofs consist of two group elements (in a pairing-free group). Compared to the pairing-based SNARGs of [Gro16], our arguments are half as long (64 bytes vs. 127 bytes), and moreover, with a precomputed verification table, the verification complexity of our SNARG requires only 2 group exponentiations (and 2 multiplications), which is faster than that of [Gro16], which requires 3 pairing operations and multiple exponentiations/multiplications. Compared to [BCI+13], our SNARGs are based on linear PCPs rather than classical PCPs, so they also enjoy concretely-efficient prover complexities for small circuits. At the same time, compared to [Gro16], our constructions are in the designated-verifier setting, have a quadratic-size CRS (as opposed to a linear-size CRS), and provide inverse polynomial soundness (as opposed to negligible soundness). However, the fast verification time and shorter proof size make our construction naturally suited for a number of scenarios (see Sect. 1.1).
-
Laconic arguments with 2 group elements and negligible soundness: The SNARGs obtained by combining a 1-query linear PCP in conjunction with ElGamal encryption have inverse polynomial soundness error. This limitation is due to two factors: (1) the linear PCP verification procedure is non-linear in the responses (for both the original [BCI+13] proposal based on standard PCPs as well as the linear PCPs obtained via our packing transformation); and (2) decryption in the (additively homomorphic variant of) ElGamal encryption requires computing a discrete log. If however we can construct a 1-query linear PCP with negligible soundness error and where the decision procedure is linear, then we can apply the [BCI+13] compiler (with ElGamal) to obtain a 2-element SNARG with negligible soundness error. On the one hand, [Gro16] previously showed a lower bound that such a linear PCP cannot exist. However, this previous lower bound only applies if the underlying linear PCP has sufficiently small completeness error (see the full version of this paper). In this work, by relying on hardness of approximation for problems related to linear codes, we obtain a 1-query linear PCP with a linear decision procedure, negligible soundness error, and o(1) completeness error. The linear PCP we obtain has the property that the verifier’s queries depend on the statement, and as such, we do not obtain a SNARG via the [BCI+13] compiler. Instead, we obtain the first laconic argument for \(\mathsf {NP} \) where the prover’s message consists of just 2 group elements and has negligible soundness error (either unconditionally in the generic group model or assuming linear targeted malleability of ElGamal).
-
Laconic arguments with 1 group element: We then turn to the question of whether we can further reduce the communication complexity. Here, under a yet-unproven, but highly plausible, hypothesis on the hardness of approximating the minimal distance of linear codes (Hypothesis 5.2), we construct a 2-message laconic argument for \(\mathsf {NP} \) where the prover’s message consists of just a single group element. We note that while there is a linear PCP associated with this language, our 1-element laconic argument construction does not follow the [BCI+13] compiler, and it is not clear how to leverage the [BCI+13] compiler to obtain an argument system where the proof is a single group element. Instead, we give a direct construction of a 1-element laconic argument that is provably secure in the generic group model.
We summarize our main new constructions of SNARGs and laconic arguments in Table 1 and also compare against existing results.
From laconic arguments to witness encryption. Several works [FNV17, BISW18, BDRV18] have studied the connection between laconic arguments and different types of encryption schemes. Notably, Faonio et al. [FNV17] show that any (even non-laconic) argument of knowledge for a language \(\mathcal {L}\) where the verifier can predict in advance the prover’s message implies an extractable witness encryption [GGSW13] scheme for \(\mathcal {L}\). As noted in [FNV17], their construction also shows an equivalence between predictable arguments (without knowledge) and (non-extractable) witness encryption.
Boneh et al. [BISW18] subsequently showed that any 1-bit argument system is predictable for languages that are hard on average. In this work, we show that a conceptually-similar result holds for argument systems where the proof consists of a single group element. In particular, we show that any such argument system that has negligible soundness error, and where the verification algorithm can be implemented by a “generic” algorithm (i.e., it only performs generic group operations on the proof), must also be predictable. By [FNV17], such an argument system for a language \(\mathcal {L}\) implies a witness encryption scheme for \(\mathcal {L}\).
As noted above, if our hypothesis on the hardness of approximation for the minimal distance of linear codes holds, then we obtain a laconic argument for \(\mathsf {NP} \) with negligible soundness error and where the proof consists of a single group element in the generic group model. Appealing now to the results above, this implies a witness encryption scheme for \(\mathsf {NP} \) in the generic group model. We stress that, in the generic group model, this result does not rely on any cryptographic assumptions; it only relies on a plausible hardness of approximation result that may be unconditionally proved in the future. Indeed, there are no known barriers for strengthening the current hardness results to this more demanding parameter regime [Kho20]. Existing constructions of witness encryption all rely on conjectures related to indistinguishability obfuscation [GGH+13], multilinear maps [GGSW13, GLW14, CVW18], or new and yet unexplored algebraic structures [BIJ+20]; thus, a construction in the generic group model would be considered a major development in this area.
Another intriguing implication of this result is that it effectively rules out negative results for constructing witness encryption unconditionally in the generic group model. Such negative results (or barriers) are not only known for powerful primitives such as indistinguishability obfuscation [MMN+16a, MMN+16b], but also for conceptually-simpler primitives such as identity-based encryption [PRV12]. Note that even though identity-based encryption can be built from witness encryption for \(\mathsf {NP} \) (together with a unique signature scheme) [GGSW13], the resulting construction makes non-black-box use of the group. Thus, a construction of witness encryption in the generic group model does not conflict with existing lower bounds. Indeed, an impossibility result for constructing witness encryption in the generic group model would falsify our hypothesis.
1.1 Concretely-Efficient SNARGs with 2 Group Elements
In this section, we provide an overview of our concretely-efficient SNARGs where the proof consists of 2 group elements. Our starting point in this work is the compiler from [BCI+13] (also implicit in [GGPR13]) that compiles a linear PCP into a SNARG in the preprocessing model using a “linear-only” encryption scheme (i.e., an additively-homomorphic encryption scheme that only supports affine operations on ciphertexts).Footnote 3 Here, the preprocessing model refers to a SNARG where the running time of the setup algorithm is allowed to depend polynomially in the size of the classic \(\mathsf {NP} \) verifier. We begin with a brief overview of this compiler.
Linear PCPs. A linear PCP for an \(\mathsf {NP} \) language \(\mathcal {L}\) over a finite field \(\mathbb {F}\) is defined by a linear oracle \(\varvec{\pi }:\mathbb {F}^\ell \rightarrow \mathbb {F}\). On a query \(\mathbf {q}\in \mathbb {F}^\ell \), the linear PCP oracle responds with the inner product \(\mathbf {q}^\mathsf {T}\varvec{\pi }\). More generally, we can view the linear PCP queries as the columns of a query matrix \(\mathbf {Q}\in \mathbb {F}^{\ell \times k}\) and the oracle’s operation as computing \(\mathbf {Q}^\mathsf {T}\varvec{\pi }\). To verify a proof of a statement \(\mathbf {x}\), the verifier submits a query matrix \(\mathbf {Q}\) to the oracle and receives back a set of responses \(\mathbf {Q}^\mathsf {T}\varvec{\pi }\). In this case, k denotes the number of linear PCP queries the verifier makes. For the language of Boolean circuit satisfiability, there exist efficient 3-query linear PCPs based on the quadratic span programs of [GGPR13] with query length \(\ell = O(s)\), where s is the size of the Boolean circuit. We can also construct 2-query linear PCPs based on the Walsh-Hadamard code where \(\ell = O(s^2)\). This improves the 3-query construction from [ALM+98, IKO07].
The Bitansky et al. compiler. The Bitansky et al. [BCI+13] compiler takes any linear PCP and a linear-only encryption scheme and outputs a preprocessing SNARG. If the linear PCP satisfies additional properties such as zero-knowledge or knowledge soundness, then the resulting SNARG also inherits those properties (i.e., we can obtain a “zkSNARK”). The idea behind the [BCI+13] compiler is the following: first, they compile a linear PCP into a two-message linear interactive proof (LIP) by introducing an additional consistency check. In this model, the prover is allowed to compute any affine function of the verifier’s queries (the linear PCP model is more constrained in the sense that the prover has to apply the same linear function to each of the verifier’s queries). To go from a LIP to a preprocessing SNARG, [BCI+13] has the verifier encrypt its queries using a linear-only encryption scheme and publish the ciphertexts as part of the common reference string (CRS). To construct a proof, the prover takes its statement and witness, computes the linear function \(\varvec{\pi }\), and homomorphically evaluates \(\varvec{\pi }\) on the encrypted queries (this is possible since the prover’s strategy is linear). The proof is the encrypted set of responses. In the designated-verifier model, the verifier decrypts the responses and applies the standard LIP verification procedure (if the verifier’s decision procedure is quadratic, a pairing can be used to perform the verification check “in the exponent,” yielding a publicly-verifiable SNARG). Overall, the [BCI+13] compiler takes any k-query linear PCP and compiles it into a preprocessing SNARG where the proofs consist of \((k + 1)\) ciphertexts of the underlying linear-only encryption scheme. Under the assumption that the classic ElGamal encryption scheme [ElG84] is linear-only (when the message is encrypted in the exponent), this framework can be used to obtain a SNARG where the proof size consists of \((k + 1)\) ElGamal ciphertexts, or equivalently, \(2(k+1)\) group elements.
1-query linear PCPs. First, we note that any 1-query linear PCP is itself a 2-message linear interactive proof, and hence, can be directly compiled into a preprocessing SNARG via the [BCI+13] compiler where the proof consists of just a single ciphertext (i.e., 2 group elements in the case of ElGamal). However, as noted above, efficient instantiations of linear PCPs based on the Hadamard PCP [ALM+98, IKO07], quadratic span programs [GGPR13] or square span programs [DFGK14, Gro16] all require at least 2 queries, and thus, cannot be directly compiled into a preprocessing SNARG with 2 group elements. If we start instead from a traditional PCP, then [BCI+13] shows how to construct a 1-query linear PCP, which in conjunction with ElGamal encryption, yields a SNARG with 2-group elements (and inverse polynomial soundness). However, the use of traditional PCPs in this construction incurs a high concrete cost, and as a result, the concrete efficiency of the resulting SNARG is not competitive with existing pairing-based constructions based on efficient linear PCPs. Furthermore, the low entropy of the queries in the PCP-based construction from [BCI+13] prevents the scheme from achieving reusable soundness.Footnote 4 In this work, we introduce a new approach to constructing 1-query linear PCPs without relying on traditional PCPs. The resulting 1-query linear PCP has reusable soundness.
Linear PCP packing. Our first result in this work is a method to pack a k-query linear PCP into a 1-query linear PCP. Our packing construction is most naturally viewed by considering a linear PCP over the integers.Footnote 5 Namely, consider a linear PCP where both the query matrix \(\mathbf {Q}\in \mathbb {Z}^{\ell \times k}\) and the proof \(\varvec{\pi }\in \mathbb {Z}^\ell \) consist of vectors over the integers. Clearly, any linear PCP over a finite field \(\mathbb {F}_p\) yields a linear PCP over the integers \(\mathbb {Z}\). We now say that a linear PCP is B-bounded if for an honestly-generated query matrix \(\mathbf {Q}\in \mathbb {Z}^{\ell \times k}\) and proof vector \(\varvec{\pi }\in \mathbb {Z}^\ell \), it follows that  (i.e., the magnitude of every response is less than B). Let \(\mathbf {q}_1, \ldots , \mathbf {q}_k \in \mathbb {Z}^\ell \) be the individual queries (i.e., the columns of \(\mathbf {Q}\)). Consider the vector \(\mathbf {q}_{\text {packed}} = \sum _{i \in [k]} B^{i-1} \mathbf {q}_i \in \mathbb {Z}^\ell \). Then,
(i.e., the magnitude of every response is less than B). Let \(\mathbf {q}_1, \ldots , \mathbf {q}_k \in \mathbb {Z}^\ell \) be the individual queries (i.e., the columns of \(\mathbf {Q}\)). Consider the vector \(\mathbf {q}_{\text {packed}} = \sum _{i \in [k]} B^{i-1} \mathbf {q}_i \in \mathbb {Z}^\ell \). Then,
If  , then a represents an integer in base B where the \({i}^{\mathrm {th}}\) digit is the \({i}^{\mathrm {th}}\) response \(\mathbf {q}_i^\mathsf {T}\varvec{\pi }\). Thus, by making a single query \(\mathbf {q}_{\text {packed}}\) (with much larger coefficients), the verifier is able to decode all k responses and implement the verification procedure for the underlying linear PCP. As described, the above approach is not sound: namely, an adversary can choose a malicious proof vector \(\varvec{\pi }\) such that \(\mathbf {Q}^\mathsf {T}\varvec{\pi }\) is not B-bounded: then, the tuple of responses decoded using the above procedure would yield a tuple that is not consistent with applying a single consistent linear strategy to all of the query vectors. We solve this problem by randomizing the query-packing procedure. Namely, instead of using a fixed scaling factor B, the verifier sets \(r_1 = 1\) and samples \(r_2, \ldots , r_k\) from a sufficiently-large interval and computes the packed query vector as \(\mathbf {q}_{\text {packed}} = \sum _{i \in [k]} \mathbf {q}_i \prod _{j \le i} r_j\). We can now argue that over the verifier’s randomness, any adversarial strategy that exceeds the bound will cause the verifier to reject with high probability. We give the construction and analysis in Sect. 3.
, then a represents an integer in base B where the \({i}^{\mathrm {th}}\) digit is the \({i}^{\mathrm {th}}\) response \(\mathbf {q}_i^\mathsf {T}\varvec{\pi }\). Thus, by making a single query \(\mathbf {q}_{\text {packed}}\) (with much larger coefficients), the verifier is able to decode all k responses and implement the verification procedure for the underlying linear PCP. As described, the above approach is not sound: namely, an adversary can choose a malicious proof vector \(\varvec{\pi }\) such that \(\mathbf {Q}^\mathsf {T}\varvec{\pi }\) is not B-bounded: then, the tuple of responses decoded using the above procedure would yield a tuple that is not consistent with applying a single consistent linear strategy to all of the query vectors. We solve this problem by randomizing the query-packing procedure. Namely, instead of using a fixed scaling factor B, the verifier sets \(r_1 = 1\) and samples \(r_2, \ldots , r_k\) from a sufficiently-large interval and computes the packed query vector as \(\mathbf {q}_{\text {packed}} = \sum _{i \in [k]} \mathbf {q}_i \prod _{j \le i} r_j\). We can now argue that over the verifier’s randomness, any adversarial strategy that exceeds the bound will cause the verifier to reject with high probability. We give the construction and analysis in Sect. 3.
We have now shown how to pack a k-query linear PCP over the integers to obtain a 1-query linear PCP over the integers. To apply the [BCI+13] compiler, we require a linear PCP over a finite field \(\mathbb {F}\). Here, we note that we can directly embed the operations over the integers into a sufficiently large finite field (e.g., if \(B_{\text {packed}}\) is a bound on \(\mathbf {q}_{\text {packed}}^\mathsf {T}\varvec{\pi }\), it suffices to work over a field \(\mathbb {F}_p\) where \(p > 2 B_{\text {packed}}\)). If we start with a linear PCP over \(\mathbb {F}_p\) and desire a packed linear PCP over the same field \(\mathbb {F}_p\), then the linear PCP responses should be small.Footnote 6 We refer to the resulting linear PCP as a “bounded” linear PCP over \(\mathbb {F}_p\). The Hadamard linear PCP has this property, so using our basic query-packing transformation, we obtain a 1-query bounded linear PCP over \(\mathbb {F}_p\) with query length \(\ell = O(s^2)\), where s is the size of the \(\mathsf {NP} \) verification circuit. A natural question is whether we can obtain a 1-query linear PCP with query length O(s) starting from the quadratic span programs of [GGPR13]. As we explain in the full version of this paper, we are not able to leverage our packing transformation because the queries in those constructions have large coefficients, and thus, do not seem directly amenable to our packing approach.
Concretely-efficient 2-element SNARGs. Starting from our 1-query linear PCP above, we directly invoke the [BCI+13] compiler with ElGamal encryption to obtain a designated-verifier SNARG in the preprocessing model where the proof consists of 2 group elements. One caveat with ElGamal is that the scheme encodes the message in the exponent (i.e., the decryption algorithm recovers \(g^a\) rather than a). In the context of the [BCI+13] compiler, this means the linear PCP response is in the exponent, and the verifier has to solve discrete log in order to verify the proofs; if the size of the response is B-bounded, this can be done in time \(\widetilde{O}(\sqrt{B})\) using Pollard’s kangaroo algorithm [Pol78]. For this to be efficient, we thus require that the responses are in a polynomial-size interval. Of course, this means that the soundness achievable using the ElGamal instantiation will be inverse polynomial in the security parameter (rather than negligible). This is because there are now only polynomially-many possible values that causes the verifier to accept, so a malicious prover can guess an accepting value with \(1/\mathsf {poly} \) probability. This yields a trade-off between the soundness error \(\varepsilon \) and the verifier’s time complexity (namely, smaller soundness error means that the responses have to be drawn from a larger interval, which increases the running time of the discrete log algorithm). Thus, when compiling linear PCPs to SNARGs using ElGamal, it is natural to consider bounded linear PCPs, which provide a direct trade-off between soundness error and the bound (see Corollary 3.4).
The bound on our 1-query linear PCP based on the Hadamard construction scales with \(O(s^4)\), which means the resulting ElGamal-based SNARG will have verification complexity that scales quadratically with the circuit size. This is both undesirable and impractical for real scenarios. However, by taking advantage of the structure of the Hadamard linear PCP, we can reduce the verification complexity to \(\widetilde{O}(\sqrt{s}/\varepsilon )\) if we allow for a negligible completeness error (as opposed to perfect completeness). The high-level idea here is that in the Hadamard linear PCP, one of the (unpacked) query responses is small and lies in an interval of size \(\widetilde{O}(\sqrt{s}/\varepsilon )\) with overwhelming probability. This means that instead of having the verifier solve the discrete log to obtain the full linear PCP response, the verifier can instead check whether the decrypted response corresponds to one of the (polynomially-many) accepting values of the Hadamard linear PCP. Thus, we obtain a designated-verifier SNARG with \(1/\mathsf {poly} \) soundness where the proof consists of exactly 2 group elements and the verifier runs in time \(\widetilde{O}(\sqrt{s}/\varepsilon )\). We provide the details in Sect. 3.2.
Preprocessing to achieve constant running time. Our approach for reducing the verification time in the ElGamal-based SNARG described above relies on there only being a small number of accepting values (that depend on the statement and the verifier’s secret key). In Sect. 3.2, we show that at setup time, the verifier can perform a statement-independent preprocessing step (which only depends on the verifier’s secret verification state) and prepare a lookup table of size \(\widetilde{O}(\sqrt{s}/\varepsilon )\). With this lookup table, the verification procedure reduces to performing 2 exponentiations and 2 group multiplications, followed by a single table lookup. This yields a much faster verification procedure compared to even the SNARG from [Gro16], which requires computing 3 pairing relations (in addition to multiple exponentiations and group multiplications). In this model, we obtain SNARGs that are both 50% shorter than those from [Gro16] (64 bytes for our construction vs. 127 bytes for [Gro16, SCI20]) and significantly faster to verify. Based on timings provided in libsnark [SCI20], the verifier’s running time in [Gro16] is 1.2 ms, while based on our estimates, two group exponentiations and two multiplications would take 0.1 ms, which is over 10x faster (see Sect. 3.3 for details on our performance estimates). This makes our designated-verifier SNARGs well-suited for environments that demand very succinct proofs and low-latency or low-energy verification.
Concrete efficiency estimates. In Table 2, we provide estimates on the size of the CRS, the prover complexity, and the verification complexity. With preprocessing, the primary cost for the verifier is the storage of the lookup table and without preprocessing, the primary cost is the verification time. Here, we apply the additional (standard) transformation to obtain a zkSNARK (described in Sect. 3.2 and Remark 3.9). We describe our methodology for computing these estimates in Sect. 3.3.
The main appeal of our new designated-verifier zkSNARKs is that with preprocessing, it has extremely lightweight verification. The proofs consist of just two group elements and with a modestly-sized lookup table (e.g., for circuits with over 15,000 wires and soundness 1/128, a lookup table of size just over 20 MB suffices). Our schemes are well suited in scenarios where the verifier has a modest amount of memory, but is otherwise low energy or computationally constrained. They are also well-suited in settings where the verifier might be receiving and authenticating requests from a large number of provers.
One appealing application is to combine the zkSNARK with a one-way function to construct an identification scheme. Here, a user’s secret key is a random element in the domain of a one-way function and the public key is its image under the one-way function. To authenticate, the user would provide a zkSNARK proving knowledge of their secret key (i.e., the pre-image under the one-way function) associated with their public key. One way to instantiate the required one-way function is to use Goldreich’s simple one-way function based on expander graphs [Gol00], which can be computed by a Boolean circuit with just 1200 gates [BIJ+20] (or 1500 wires). In this case, the CRS size is around 34 MB and the prover’s computation would take just a few seconds of computation. With a moderate soundness level of 1/128, the verifier only needs to maintain a table with just over 6 MB of storage. If the bottleneck in the system is sending proofs and authenticating credentials, then our construction offers a compelling solution. Moreover, the expressive nature of zkSNARKs lends itself naturally towards implementing more complex authentication policies (e.g., the user’s credential is valid and moreover, satisfies some simple Boolean predicate).
While our construction achieves a lower level of soundness compared to pairing-based alternatives, scenarios where there are severe out-of-band consequences for getting caught cheating (even once) can provide strong incentives for honest behavior. This is conceptually similar to the notion of covert security in multiparty computation [CO99, AL07]. Similarly, while our constructions do not provide perfect zero-knowledge, the effects of any potential leakage can be mitigated (in the above setting with an identification scheme) by using a leakage-resilient one-way function. Moreover, in the setting of short-lived tokens or credentials, the user can simply refresh their credential after a certain number of requests (based on the zero-knowledge parameter of the system).
More broadly, we believe that our new preprocessing zkSNARKs are appealing in terms of proof size and verifier complexity. It is interesting to further optimize our methods to support more complex circuits. In the full version of this paper, we describe one approach based on constructing specially-designed circuits that are “Hadamard-friendly,” which can then be efficiently-checked using a linear PCP (with small amortized query size), and correspondingly, enable a more concretely efficient zkSNARK.
1.2 From Hardness of Approximation to Witness Encryption
A limitation of the SNARG constructions based on instantiating the [BCI+13] compiler with ElGamal is that they only provide \(1/\mathsf {poly} \) soundness. Part of this stems from the inherent challenge that recovering the linear PCP responses from an ElGamal ciphertext requires computing discrete log, which restricts us to linear PCPs whose responses lie in a polynomial-size set (and correspondingly, yields SNARGs with inverse polynomial soundness error). However, Bitansky et al. [BCI+13] point out that if we had a linear PCP with a linear decision procedure and if we apply the compiler using ElGamal encryption, the verifier no longer needs to decrypt the responses. Instead, it can simply check the verification procedure “in the exponent.” This provides a general template for constructing a succinct argument based on ElGamal that can achieve negligible soundness error. While Bitansky et al. motivate the search for a linear PCP with a linear decision procedure, they do not suggest a candidate.
1-query linear PCP with negligible soundness from hardness of approximation. In this work, we introduce a new approach for constructing linear PCPs based on the hardness of approximating problems related to decoding linear codes. Specifically, we construct a 1-query linear PCP with a linear decision procedure and negligible soundness error. Our construction affirmatively answers the above question posed by Bitansky et al. on whether there exists a linear interactive proof with a linear decision procedure. We note, however, that the linear PCP we construct is instance-dependent (i.e., the verifier’s query depends on the statement being verified). As such, applying the [BCI+13] compiler yields a 2-message laconic argument where the prover’s message consists of 2 group elements.
Previously, Groth [Gro16] ruled out the possibility of 2-message linear interactive proofs with a linear decision procedure for languages that are hard on average. Implicit in his lower bound is the assumption that the underlying proof satisfies perfect completeness (or more generally, has sufficiently small completeness error). Our 1-query linear PCP construction has a small, but noticeable, o(1) completeness error which avoids this lower bound. We discuss this in greater detail in the full version of this paper.
Our linear PCP construction relies on the hardness of approximation for the gap minimum weight solution problem (\(\mathsf {GapMWSP} \)) [KPV12]. At a high level, a problem instance for \(\mathsf {GapMWSP} _\beta \) is a triple \((\mathbf {A}, \mathbf {b}, d)\) where \(\mathbf {A}\in \mathbb {F}^{\ell \times n}\), \(\mathbf {b}\in \mathbb {F}^\ell \), \(d \in \mathbb {N}\), and \(\mathbb {F}\) is a finite field. The goal is to decide whether there exists a solution \(\mathbf {x}\in \mathbb {F}^n\) with Hamming weight at most d such that \(\mathbf {A}\mathbf {x}= \mathbf {b}\), or, alternatively, if all solutions \(\mathbf {x}\in \mathbb {F}^n\) to the linear system \(\mathbf {A}\mathbf {x}= \mathbf {b}\) have Hamming weight at least \(\beta \cdot d\), where \(\beta = \mathsf {polylog}(n)\) is the approximation factor. While this problem is traditionally formulated over the binary field \(\mathbb {F}_2\), we show that the same \(\mathsf {NP} \)-hardness reduction (from the \(\mathsf {GapLabelCover} \) problem [Raz95]) extends to general finite fields.
We can construct a linear PCP for the \(\mathsf {GapMWSP} \) problem in a straightforward manner (this in turn yields a linear PCP for \(\mathsf {NP} \) by first applying a Karp-Levin reduction to \(\mathsf {GapMWSP} \)). The linear PCP query for an instance \((\mathbf {A}, \mathbf {b}, d)\) consists of a random vector \(\mathbf {r}{\mathop {\leftarrow }\limits ^{\textsc {r}}}\mathbb {F}^\ell \) and a sparse vector \(\mathbf {e}\in \mathbb {F}^n\) where each component of \(\mathbf {e}\) is either uniform over \(\mathbb {F}\) or 0. The query is the vector \(\mathbf {q}^\mathsf {T}= \mathbf {r}^\mathsf {T}\mathbf {A}+ \mathbf {e}^\mathsf {T}\in \mathbb {F}^n\). The proof for an instance \((\mathbf {A}, \mathbf {b}, d)\) is a vector \(\varvec{\pi }\in \mathbb {F}^n\) where \(\mathbf {A}\varvec{\pi }= \mathbf {b}\) and \(\varvec{\pi }\) has small Hamming weight \(\mathsf {wt}(\varvec{\pi }) \le d\). Finally, given a response \(a \in \mathbb {F}\), the verifier simply checks whether \(a = \mathbf {r}^\mathsf {T}\mathbf {b}\). Suppose that \(\mathbf {A}\varvec{\pi }= \mathbf {b}\). Then, \(\mathbf {q}^\mathsf {T}\varvec{\pi }= \mathbf {r}^\mathsf {T}\mathbf {A}\varvec{\pi }+ \mathbf {e}^\mathsf {T}\varvec{\pi }= \mathbf {r}^\mathsf {T}\mathbf {b}+ \mathbf {e}^\mathsf {T}\varvec{\pi }\). Completeness follows as long as \(\mathbf {e}^\mathsf {T}\varvec{\pi }= 0\). This happens with \(1 - o(1)\) probability since both \(\mathbf {e}\) and \(\varvec{\pi }\) are sparse (i.e., \(\mathbf {e}^\mathsf {T}\varvec{\pi }\) is nonzero only if both \(\mathbf {e}\) and \(\varvec{\pi }\) have a nonzero component in the same coordinate, which happens with small, but noticeable, probability over the randomness of \(\mathbf {e}\)). Conversely, for a no instance, all solutions to the linear system \(\mathbf {A}\mathbf {x}= \mathbf {b}\) have Hamming weight at least \(\beta d\). In this case, for any proof vector \(\varvec{\pi }\), either \(\mathbf {A}\varvec{\pi }\ne \mathbf {b}\) (in which case, the verifier rejects except with probability  over the randomness of \(\mathbf {r}\)) or if \(\mathbf {A}\varvec{\pi }= \mathbf {b}\), then \(\varvec{\pi }\) has large Hamming weight and \(\mathbf {e}^\mathsf {T}\varvec{\pi }\) will be nonzero with overwhelming probability over the choice of \(\mathbf {e}\). Hence, we obtain an instance-dependent 1-query linear PCP with a linear decision procedure from the \(\mathsf {GapMWSP} \) problem, and correspondingly, a 2-message laconic argument with negligible soundness and where the proof size consist of just 2 group elements by invoking the
[BCI+13] compiler with ElGamal encryption. We provide the full description and analysis in Sect. 4.
over the randomness of \(\mathbf {r}\)) or if \(\mathbf {A}\varvec{\pi }= \mathbf {b}\), then \(\varvec{\pi }\) has large Hamming weight and \(\mathbf {e}^\mathsf {T}\varvec{\pi }\) will be nonzero with overwhelming probability over the choice of \(\mathbf {e}\). Hence, we obtain an instance-dependent 1-query linear PCP with a linear decision procedure from the \(\mathsf {GapMWSP} \) problem, and correspondingly, a 2-message laconic argument with negligible soundness and where the proof size consist of just 2 group elements by invoking the
[BCI+13] compiler with ElGamal encryption. We provide the full description and analysis in Sect. 4.
From laconic arguments to witness encryption. Given a laconic argument where the proof consists of just two group elements, a natural question to ask is whether we can have an argument that is even shorter: namely, a laconic argument with just a single group element. From a conceptual perspective, this question has a similar flavor to the notion of a “1-bit SNARG” introduced in [BISW18]. There, they showed that a 1-bit SNARG for a hard language is in fact “predictable” (i.e., the verifier can predict the value of an accepting proof), and by leveraging the result from [FNV17], implies a witness encryptionFootnote 7 scheme for the underlying language. As it turns out, laconic arguments where the prover’s message is a single group element and where the verification algorithm only consists of generic group operations are similarly powerful. As we show in the full version of this paper, any 1-element laconic argument that has negligible soundness error and a “generic” verification algorithm (i.e., it only performs algebraic operations over group elements) implies witness encryption for the underlying language. This means that improving our 2-element laconic argument to a 1-element laconic argument provides a promising new path towards realizing witness encryption from more traditional and well-understood cryptographic assumptions.
1-element laconic argument from hardness of approximation. It is not clear how to leverage our 1-query linear PCP from the \(\mathsf {GapMWSP} \) problem to obtain a laconic argument where the proof consists of just a single group element. Indeed, any application of the [BCI+13] compiler with ElGamal would yield an argument system where the proof consists of at least 2 group elements (since the proof will contain at least one ElGamal ciphertext). However, we show that assuming a conceptually-similar, but yet-unproven hypothesis on the hardness of approximating the minimal distance of linear codes, we can leverage similar ideas used to construct our linear PCP from \(\mathsf {GapMWSP} \) to directly construct a 1-element laconic argument with negligible soundness in the generic group model. The resulting argument is predictable in the sense of [FNV17] (even without applying our generic transformation above), and thus, implies a witness encryption scheme for \(\mathsf {NP} \) in the generic group model. While the hypothesis we rely on is unproven, there are no known barriers for extending the current hardness of approximation results for the minimal distance problem to the more challenging parameter regime needed for our construction [Kho20].
Our 1-element laconic argument relies on the hardness of approximating the minimal distance of a linear code (\(\mathsf {GapMDP} \)). For an approximation factor \(\beta > 0\), a \(\mathsf {GapMDP} _\beta \) instance \((\mathbf {A}, d)\) consists of a matrix \(\mathbf {A}\) (over a finite field \(\mathbb {F}\)) and a distance \(d \in \mathbb {N}\) and the problem is to decide whether the minimum distance (under the Hamming metric) of the code generated by \(\mathbf {A}\) is less than d or greater than \(\beta \cdot d\). Equivalently, we can formulate the problem as distinguishing between the following two possibilities with respect to the parity-check matrix \(\mathbf {H}\in \mathbb {F}^{\ell \times k}\) of the code generated by \(\mathbf {A}\).
-
There exists a nonzero vector \(\mathbf {0}\ne \mathbf {v}\in \mathbb {F}_p^\ell \) with Hamming weight at most d such that \(\mathbf {H}\mathbf {v}= \mathbf {0}\).
-
For all nonzero vectors \(\mathbf {0}\ne \mathbf {v}\in \mathbb {F}_p^\ell \) with Hamming weight up to \(\beta \cdot d\), \(\mathbf {H}\mathbf {v}\ne \mathbf {0}\).
When \(\beta = \omega (\log n)\), it is not difficult to construct a 1-element laconic argument for the \(\mathsf {GapMDP} _\beta \) language with negligible soundness. We use the same principles we used to construct the 1-query linear PCP for \(\mathsf {GapMWSP} _\beta \). The construction operates over a group \(\mathbb {G}\) of prime order p with generator g (which we will model as a generic group for the security analysis). The construction works as follows:
-
Query generation: The verifier samples random vectors \(\mathbf {c}{\mathop {\leftarrow }\limits ^{\textsc {r}}}\mathbb {F}_p^k\) \(\mathbf {r}{\mathop {\leftarrow }\limits ^{\textsc {r}}}\mathbb {F}_p^k\) and a scalar \(s {\mathop {\leftarrow }\limits ^{\textsc {r}}}\mathbb {F}_p\). It also samples a noise vector \(\mathbf {e}\in \mathbb {F}_p^k\), where the entries of \(\mathbf {e}\) are either 0 or uniform over \(\mathbb {F}_p\). The density of \(\mathbf {e}\) is chosen to balance the completeness and soundness requirements. The verifier computes \(\mathbf {z}^\mathsf {T}= \mathbf {r}^\mathsf {T}\mathbf {H}+ s \mathbf {c}^\mathsf {T}+ \mathbf {e}^\mathsf {T}\in \mathbb {F}_p^k\). The query is the pair \((\mathbf {c}, g^{\mathbf {z}})\) where \(g^\mathbf {z}\) denotes the vector of group elements \(g^{z_1}, \ldots , g^{z_k}\), and \(\mathbf {z}= (z_1, \ldots , z_k)\).
-
Prover’s response: For an \(\textsc {yes} \) instance to the \(\mathsf {GapMDP} \) problem, the witness is a vector \(\mathbf {v}\in \mathbb {F}_p^k\) such that \(\mathbf {H}\mathbf {v}= \mathbf {0}\) and \(\mathbf {v}\) has low Hamming weight. On input the query \(\mathbf {c}\) and \(g^{\mathbf {z}}\) and the witness \(\mathbf {v}\in \mathbb {F}_p^k\), the prover computes \(t = (\mathbf {c}^\mathsf {T}\mathbf {v})^{-1}\) and replies with the single group element \(g^{t \cdot \mathbf {z}^\mathsf {T}\mathbf {v}}\).
-
Verification: To verify the proof \(\pi \), the verifier checks that \(\pi = g^{s}\).
We now informally describe the completeness and soundness analysis:
-
Completeness: For a \(\textsc {yes} \) instance, the witness \(\mathbf {v}\) satisfies \(\mathbf {H}\mathbf {v}= \mathbf {0}\) and moreover \(\mathbf {v}\) has low Hamming weight. If the noise vector \(\mathbf {e}\) is sufficiently sparse, then with high probability, \(\mathbf {e}^\mathsf {T}\mathbf {v}= 0\). Thus,
$$\begin{aligned} \mathbf {z}^\mathsf {T}\mathbf {v}= \mathbf {r}^\mathsf {T}\mathbf {H}\mathbf {v}+ s \mathbf {c}^\mathsf {T}\mathbf {v}+ \mathbf {e}^\mathsf {T}\mathbf {v}= s \mathbf {c}^\mathsf {T}\mathbf {v}. \end{aligned}$$In this case, \(g^{t \cdot \mathbf {z}^\mathsf {T}\mathbf {v}} = g^{s}\) since \(t = (\mathbf {c}^\mathsf {T}\mathbf {v})^{-1}\). Note that \(\mathbf {c}\) is uniform (and independent of \(\mathbf {v}\)), so the quantity \(\mathbf {c}^\mathsf {T}\mathbf {v}\) is nonzero with overwhelming probability (and thus, invertible).
-
Soundness: For the soundness analysis, we model the group as a generic group. Since the prover only has an encoding \(g^{\mathbf {z}}\) of \(\mathbf {z}\in \mathbb {F}_p^k\), in the generic group model, the only components that it can construct are of the form \(g^{\mathbf {z}^\mathsf {T}\varvec{\alpha }+ \beta }\) for some choice of \(\varvec{\alpha }\in \mathbb {F}_p^k\) and \(\beta \in \mathbb {F}_p\). The prover succeeds if it is able to find \(\varvec{\alpha }, \beta \) such that \(\mathbf {z}^\mathsf {T}\varvec{\alpha }+ \beta = \mathbf {r}^\mathsf {T}\mathbf {H}\varvec{\alpha }+ s \mathbf {c}^\mathsf {T}\varvec{\alpha }+ \mathbf {e}^\mathsf {T}\varvec{\alpha }= s\). We consider two possibilities:
-
If the Hamming weight of \(\varvec{\alpha }\) is less than \(\beta \cdot d\) and we have a \(\textsc {no} \) instance, then \(\mathbf {H}\varvec{\alpha }\ne \mathbf {0}\). In this case, over the randomness of \(\mathbf {r}\), the value of \(\mathbf {r}^\mathsf {T}\mathbf {H}\varvec{\alpha }\ne 0\) is uniform over \(\mathbb {F}_p\).
-
Alternatively, if \(\varvec{\alpha }\) has Hamming weight larger than \(\beta \cdot d\), and \(\mathbf {e}\) is sufficiently dense, then with overwhelming probability, there is some component \(e_i\) such that \(e_i \alpha _i \ne 0\), and so \(\mathbf {e}^\mathsf {T}\varvec{\alpha }\ne 0\). In this case, the value of \(\mathbf {e}^\mathsf {T}\varvec{\alpha }\) is uniform over \(\mathbb {F}_p\).
This means that for any choice of \(\varvec{\alpha }, \beta \) that the prover chooses, with overwhelming probability, either \(\mathbf {r}^\mathsf {T}\mathbf {H}\varvec{\alpha }\) or \(\mathbf {e}^\mathsf {T}\varvec{\alpha }\) is uniform over \(\mathbb {F}_p\) (and independent of s). The probability that \(\mathbf {z}^\mathsf {T}\varvec{\alpha }+ \beta = s\) is negligible.
-
Observe that in the above analysis, we require \(\mathbf {e}\) to be sufficiently sparse for completeness to hold with high probability and sufficiently dense for soundness to hold with overwhelming probability. For this reason, we require that the gap \(\beta \) be large enough so as to satisfy both constraints. In particular, taking \(\beta = \omega (\log n)\) suffices for our analysis. We provide the full description of the scheme and its analysis in Sect. 5.1.
To obtain a 1-element laconic argument for \(\mathsf {NP} \) (and correspondingly, a witness encryption scheme for all of \(\mathsf {NP} \)), we need to assume that the above \(\mathsf {GapMDP} _\beta \) problem is \(\mathsf {NP}\text {-}\mathsf {hard} \) for some choice of \(\beta = \omega (\log n)\) and \(\mathbb {F}_p\) is a finite field of super-polynomial size. More precisely, we require that there is a deterministic polynomial-time Karp-Levin reduction from \(\mathsf {NP} \) to \(\mathsf {GapMDP} _\beta \). Existing hardness of approximation results show that over polynomial-size fields, the \(\mathsf {GapMDP} \) problem is \(\mathsf {NP}\text {-}\mathsf {hard} \) for constant approximation factors \(\beta = O(1)\), and \(\mathsf {NP}\text {-}\mathsf {hard} \) under a deterministic quasi-polynomial time reduction for “almost-polynomial” approximation factors \(\beta = 2^{\log ^{1-\varepsilon }(n)}\). Thus, proving our hypothesis (Hypothesis 5.2) requires strengthening existing hardness results in two directions: (1) arguing \(\mathsf {NP} \)-hardness for some \(\beta = \omega (\log n)\) under a polynomial-time reduction; and (2) extending the hardness result to exponential-size prime order fields. As mentioned above, while our existing techniques do not seem sufficient, there are also no known barriers to showing the hardness of approximation results we require [Kho20]. If our hypothesis is true, then we obtain an unconditional construction of witness encryption for \(\mathsf {NP} \) in the generic group model.
2 Preliminaries
For a positive integer \(n \in \mathbb {N}\), we write [n] to denote the set  . We write \(\mathbb {F}\) to denote a finite field. We will use bold lowercase letters (e.g., \(\mathbf {v}, \mathbf {w}\)) to denote vectors and bold uppercase letters (e.g., \(\mathbf {A}, \mathbf {B}\)) to denote matrices. For a vector \(\mathbf {v}\in \mathbb {F}^n\), \(\mathsf {wt}(\mathbf {v})\) denotes the Hamming weight of \(\mathbf {v}\) (i.e., the number of nonzero entries in \(\mathbf {v}\)). For a matrix \(\mathbf {A}\in \mathbb {F}^{n\times m}\), we write \(\mathsf {dist} (\mathbf {A})\) to denote the minimum distance of the code generated by \(\mathbf {A}\). (i.e., the minimum Hamming weight of a nonzero codeword generated by \(\mathbf {A}\)).
. We write \(\mathbb {F}\) to denote a finite field. We will use bold lowercase letters (e.g., \(\mathbf {v}, \mathbf {w}\)) to denote vectors and bold uppercase letters (e.g., \(\mathbf {A}, \mathbf {B}\)) to denote matrices. For a vector \(\mathbf {v}\in \mathbb {F}^n\), \(\mathsf {wt}(\mathbf {v})\) denotes the Hamming weight of \(\mathbf {v}\) (i.e., the number of nonzero entries in \(\mathbf {v}\)). For a matrix \(\mathbf {A}\in \mathbb {F}^{n\times m}\), we write \(\mathsf {dist} (\mathbf {A})\) to denote the minimum distance of the code generated by \(\mathbf {A}\). (i.e., the minimum Hamming weight of a nonzero codeword generated by \(\mathbf {A}\)).
We write \(\lambda \) to denote a security parameter. We say that a function f is negligible in \(\lambda \), denoted \(\mathsf {negl} (\lambda )\) if \(f(\lambda ) = o(1/\lambda ^c)\) for all \(c \in \mathbb {N}\). We say an event happens with negligible probability if the probability of the event happening is negligible, and that it happens with overwhelming probability if its complement occurs with overwhelming probability. We say an algorithm is efficient if it runs in probabilistic polynomial time in the length of its input. We write \(\mathsf {poly} (\lambda )\) to denote a function that is bounded by a fixed polynomial in \(\lambda \) and \(\mathsf {polylog}(\lambda )\) to denote a function that is bounded by \(\mathsf {poly} (\log \lambda )\). We say that two families of distributions  and
and  are computationally indistinguishable (denoted \(\mathcal {D}_1 {\mathop {\approx }\limits ^{c}}\mathcal {D}_2\)) if no efficient adversary can distinguish samples from \(\mathcal {D}_1\) and \(\mathcal {D}_2\) except with negligible probability. We say that \(\mathcal {D}_1\) and \(\mathcal {D}_2\) are statistically indistinguishable (denoted \(\mathcal {D}_1 {\mathop {\approx }\limits ^{s}}\mathcal {D}_2\)) if the statistical distance between \(\mathcal {D}_1\) and \(\mathcal {D}_2\) is negligible. We review additional preliminaries in the full version of this paper.
are computationally indistinguishable (denoted \(\mathcal {D}_1 {\mathop {\approx }\limits ^{c}}\mathcal {D}_2\)) if no efficient adversary can distinguish samples from \(\mathcal {D}_1\) and \(\mathcal {D}_2\) except with negligible probability. We say that \(\mathcal {D}_1\) and \(\mathcal {D}_2\) are statistically indistinguishable (denoted \(\mathcal {D}_1 {\mathop {\approx }\limits ^{s}}\mathcal {D}_2\)) if the statistical distance between \(\mathcal {D}_1\) and \(\mathcal {D}_2\) is negligible. We review additional preliminaries in the full version of this paper.
Arithmetic circuit satisfiability. A central part of this work is constructing succinct argument systems for the language of Boolean circuit satisfiability. When describing some of our constructions however, it will oftentimes be more natural to consider the more general language of arithmetic circuit satisfiability which we recall formally below. Throughout this paper, an arithmetic circuit \(C :\mathbb {F}^n \times \mathbb {F}^h \rightarrow \mathbb {F}^\ell \) over a finite field \(\mathbb {F}\) consists of a collection of addition gates with unbounded fan-in and multiplication gates with fan-in 2. Both types of gates can have unbounded fan-out. As noted in [BCI+13], Boolean circuit satisfiability can be reduced to arithmetic circuit satisfiability over any finite field \(\mathbb {F}\) with constant overhead.
Definition 2.1
(Arithmetic Circuit Satisfiability). Let \(\mathbb {F}\) be a finite field. For an arithmetic circuit \(C :\mathbb {F}^n \times \mathbb {F}^h \rightarrow \mathbb {F}^t\) over \(\mathbb {F}\), the arithmetic circuit satisfiability problem is defined by the relation  . We write \(\mathcal {L}_C\) to denote the corresponding language. For a family of arithmetic circuits
. We write \(\mathcal {L}_C\) to denote the corresponding language. For a family of arithmetic circuits  , we write \(\mathcal {R}_{\mathcal {C}}\) and \(\mathcal {L}_{\mathcal {C}}\) to denote the infinite relation \(\mathcal {R}_{\mathcal {C}} = \bigcup _{\ell \in \mathbb {N}} \mathcal {R}_{C_\ell }\) and infinite language \(\mathcal {L}_\mathcal {C}= \bigcup _{\ell \in \mathbb {N}} \mathcal {L}_{C_\ell }\). The special case of Boolean circuit satisfiability is the problem of arithmetic circuit satisfiability over the binary field \(\mathbb {F}= \mathbb {F}_2\) (in this case, the output of C can be taken to be a single bit (i.e., \(\ell = 1\)) without loss of generality).
, we write \(\mathcal {R}_{\mathcal {C}}\) and \(\mathcal {L}_{\mathcal {C}}\) to denote the infinite relation \(\mathcal {R}_{\mathcal {C}} = \bigcup _{\ell \in \mathbb {N}} \mathcal {R}_{C_\ell }\) and infinite language \(\mathcal {L}_\mathcal {C}= \bigcup _{\ell \in \mathbb {N}} \mathcal {L}_{C_\ell }\). The special case of Boolean circuit satisfiability is the problem of arithmetic circuit satisfiability over the binary field \(\mathbb {F}= \mathbb {F}_2\) (in this case, the output of C can be taken to be a single bit (i.e., \(\ell = 1\)) without loss of generality).
2.1 Linear PCPs
We begin by recalling the definition of linear PCPs (LPCP) from [BCI+13]. Our definition combines features from a “fully linear PCP” introduced in [BBC+19] with the traditional notion of a linear PCP. First, recall that in a fully linear PCP, the verifier does not have direct access to the statement \(\mathbf {x}\in \mathbb {F}^n\) and instead is given linear query access to the vector \([\varvec{\pi }, \mathbf {x}]\) that includes the proof \(\varvec{\pi }\) together with the statement \(\mathbf {x}\). To simplify the definition (and still capture existing constructions of linear PCPs), in a k-query linear PCP, we allow the verifier to make a single “free” linear query to the statement \(\mathbf {x}\) and up to k linear queries to the proof vector \(\varvec{\pi }\). We give our definition below:
Definition 2.2
(Linear PCP
[BCI+13, BBC+19, adapted]). Let  be a binary relationFootnote 8 (with associated language \(\mathcal {L}\)) over a finite field \(\mathbb {F}\). A k-query linear PCP for \(\mathcal {R}\) with query length \(\ell \) and soundness error \(\varepsilon \) is a tuple of algorithms \(\varPi _{\mathsf {LPCP}} = (\mathcal {Q}_{\mathsf {LPCP}}, \mathcal {P}_{\mathsf {LPCP}}, \mathcal {D}_{\mathsf {LPCP}})\) with the following properties:
be a binary relationFootnote 8 (with associated language \(\mathcal {L}\)) over a finite field \(\mathbb {F}\). A k-query linear PCP for \(\mathcal {R}\) with query length \(\ell \) and soundness error \(\varepsilon \) is a tuple of algorithms \(\varPi _{\mathsf {LPCP}} = (\mathcal {Q}_{\mathsf {LPCP}}, \mathcal {P}_{\mathsf {LPCP}}, \mathcal {D}_{\mathsf {LPCP}})\) with the following properties:
-
The verifier’s query algorithm \(\mathcal {Q}_{\mathsf {LPCP}}\) outputs a query \(\mathbf {q}_{\mathsf {inp}}\in \mathbb {F}^n\), a query matrix \(\mathbf {Q}\in \mathbb {F}^{\ell \times k}\), and a verification state \(\mathsf {st}\). We can also consider an input-dependent linear PCP where the query algorithm also takes as input a statement \(\mathbf {x}\in \mathbb {F}^n\).
-
The prover algorithm \(\mathcal {P}_{\mathsf {LPCP}}\) takes a statement \(\mathbf {x}\in \mathbb {F}^n\) and a witness \(\mathbf {w}\in \mathbb {F}^h\) as input and outputs a proof \(\varvec{\pi }\in \mathbb {F}^{\ell }\).
-
The verifier’s decision algorithm \(\mathcal {D}_{\mathsf {LPCP}}\) takes as input the verification state \(\mathsf {st}\), an input-dependent response \(a_{\mathsf {inp}}\in \mathbb {F}\), and a vector of responses \(\mathbf {a}\in \mathbb {F}^k\), and outputs a bit
 .
.
In addition, \(\varPi _{\mathsf {LPCP}}\) should satisfy the following properties:
-
Completeness: For all \(\mathbf {x}\in \mathbb {F}^n\) and \(\mathbf {w}\in \mathbb {F}^h\) where \(\mathcal {R}(\mathbf {x}, \mathbf {w}) = 1\),
$$ \Pr [\mathcal {D}_{\mathsf {LPCP}}(\mathsf {st}, \mathbf {q}_{\mathsf {inp}}^\mathsf {T}\mathbf {x}, \mathbf {Q}^\mathsf {T}\varvec{\pi }) = 1\mid (\mathsf {st}, \mathbf {q}_{\mathsf {inp}}, \mathbf {Q}) \leftarrow \mathcal {Q}_{\mathsf {LPCP}}, \varvec{\pi }\leftarrow \mathcal {P}_{\mathsf {LPCP}}(\mathbf {x}, \mathbf {w})] = 1$$ -
Soundness: For every \(\mathbf {x}\notin \mathcal {L}\) and every \(\varvec{\pi }^* \in \mathbb {F}^\ell \), \(\varvec{\delta }^* \in \mathbb {F}^k\),
$$ \Pr [\mathcal {D}_{\mathsf {LPCP}}(\mathsf {st}, \mathbf {q}_{\mathsf {inp}}^\mathsf {T}\mathbf {x}, \mathbf {Q}^\mathsf {T}\varvec{\pi }^* + \varvec{\delta }^*) = 1 \mid (\mathsf {st}, \mathbf {q}_{\mathsf {inp}}, \mathbf {Q}) \leftarrow \mathcal {Q}_{\mathsf {LPCP}}] \le \varepsilon . $$ -
\(\delta \)-Honest-verifier zero-knowledge (\(\delta \)-\(\mathsf {HVZK}\)): There exists an efficient simulator \(\mathcal {S}_{\mathsf {LPCP}}\) such that for all \(\mathbf {x}\in \mathcal {L}\), the following distributions are \(\delta \)-close (i.e., their statistical distance is at most \(\delta \)):

If these two distributions are identically distributed, we say that \(\mathsf {LPCP} \) satisfies perfect honest-verifier zero-knowledge.Footnote 9
In the full version of this paper, we recall additional properties on linear PCPs.
3 1-Query Linear PCPs via Packing
In this section, we begin by introducing the notion of a bounded linear PCP over the finite field \(\mathbb {F}_p\). Throughout this section, we will view elements \(x \in \mathbb {F}_p\) as both field elements over \(\mathbb {F}_p\) as well as integers in the interval \([-p/2, p/2]\). We first show in Construction 3.2 how to pack k-query bounded linear PCPs into a 1-query linear PCP. In the full version of this paper, we describe how to construct a 2-query linear PCP based on the Hadamard linear PCP [ALM+98, IKO07]. In conjunction with our query-packing transformation, we obtain 1-query linear PCPs for \(\mathsf {NP} \). Then, by invoking the compiler from [BCI+13] with the ElGamal encryption scheme, we obtain a SNARG where the proof consists of a single ElGamal ciphertext (i.e., two group elements). Then, in Sects. 3.2 and 3.3, we show how to optimize the concrete efficiency of our ElGamal-based SNARG (by leveraging structural properties of our 1-query linear PCP).
Definition 3.1
(Bounded Linear PCP). A k-query linear PCP \(\varPi _{\mathsf {LPCP}} = (\mathcal {Q}_{\mathsf {LPCP}}, \mathcal {P}_{\mathsf {LPCP}}, \mathcal {D}_{\mathsf {LPCP}})\) for a relation  over a finite field \(\mathbb {F}_p\) is bounded with respect to bound functions \(b_1, \ldots , b_k :\mathbb {N}\rightarrow \mathbb {N}\) if \(\mathcal {Q}_{\mathsf {LPCP}}\) and \(\mathcal {P}_{\mathsf {LPCP}}\) take as input an additional bound parameter \(\tau \in \mathbb {N}\) and for any \(\mathbf {x}, \mathbf {w}\) where \(\mathcal {R}(\mathbf {x}, \mathbf {w}) = 1\), we have for all \(i \in [k]\),
over a finite field \(\mathbb {F}_p\) is bounded with respect to bound functions \(b_1, \ldots , b_k :\mathbb {N}\rightarrow \mathbb {N}\) if \(\mathcal {Q}_{\mathsf {LPCP}}\) and \(\mathcal {P}_{\mathsf {LPCP}}\) take as input an additional bound parameter \(\tau \in \mathbb {N}\) and for any \(\mathbf {x}, \mathbf {w}\) where \(\mathcal {R}(\mathbf {x}, \mathbf {w}) = 1\), we have for all \(i \in [k]\),
where \(\mathbf {q}_i\) denotes the \({i}^{\mathrm {th}}\) column on \(\mathbf {Q}\) and the inner product is computed over the integers. We say that \(\varPi _{\mathsf {LPCP}}\) is bounded with respect to bound functions \(b_1, \ldots , b_k\) with probability \(\varepsilon \) if Eq. (3.1) holds with probability \(\varepsilon \). Moreover, when defining \(\delta \)-\(\mathsf {HVZK} \) for bounded linear PCPs, we additionally provide the bound parameter \(\tau \) as input to \(\mathcal {Q}_{\mathsf {LPCP}}\) and \(\mathcal {P}_{\mathsf {LPCP}}\) in the real distribution and the simulator \(\mathcal {S}_{\mathsf {LPCP}}\) in the simulated distribution (in addition to the input x). In this case, we also allow the bound function to depend on both the bound parameter \(\tau \) as well as the zero-knowledge parameter \(\delta \).
We refer to the full version of this paper for the definition of strong soundness as it pertains to bounded linear PCPs.
Construction 3.2
(Bounded Linear PCP Packing). Let \(\varPi _{\mathsf {LPCP}}' = (\mathcal {Q}_{\mathsf {LPCP}}', \mathcal {P}_{\mathsf {LPCP}}', \mathcal {D}_{\mathsf {LPCP}}')\) be a k-query bounded LPCP for a binary relation  over \(\mathbb {F}_p\) with bound functions \(b_1', \ldots , b_k' :\mathbb {N}\rightarrow \mathbb {N}\) and soundness error \(\varepsilon '\). We will assume that \(\mathcal {D}_{\mathsf {LPCP}}'\) strictly enforces the bound on the responses (namely, given a set of responses \(a_1, \ldots , a_k\), \(\mathcal {D}_{\mathsf {LPCP}}'\) accepts only if \(a_i \in [-b_i'(\tau ), b_i'(\tau )]\) for each \(i \in [k]\); see the full version of this paper for more discussion). We construct a 1-query bounded LPCP \(\varPi _{\mathsf {LPCP}} = (\mathcal {Q}_{\mathsf {LPCP}}, \mathcal {P}_{\mathsf {LPCP}}, \mathcal {D}_{\mathsf {LPCP}})\) as follows:
over \(\mathbb {F}_p\) with bound functions \(b_1', \ldots , b_k' :\mathbb {N}\rightarrow \mathbb {N}\) and soundness error \(\varepsilon '\). We will assume that \(\mathcal {D}_{\mathsf {LPCP}}'\) strictly enforces the bound on the responses (namely, given a set of responses \(a_1, \ldots , a_k\), \(\mathcal {D}_{\mathsf {LPCP}}'\) accepts only if \(a_i \in [-b_i'(\tau ), b_i'(\tau )]\) for each \(i \in [k]\); see the full version of this paper for more discussion). We construct a 1-query bounded LPCP \(\varPi _{\mathsf {LPCP}} = (\mathcal {Q}_{\mathsf {LPCP}}, \mathcal {P}_{\mathsf {LPCP}}, \mathcal {D}_{\mathsf {LPCP}})\) as follows:
-
\(\mathcal {Q}_{\mathsf {LPCP}}(\tau )\): On input the bound parameter \(\tau \), \(\mathcal {Q}_{\mathsf {LPCP}}\) proceeds as follows:
-
1.
Run \((\mathsf {st}', \mathbf {q}_{\mathsf {inp}}', \mathbf {Q}') \leftarrow \mathcal {Q}_{\mathsf {LPCP}}'(\tau )\). Set \(\mathbf {q}_{\mathsf {inp}}= \mathbf {q}_{\mathsf {inp}}'\).
-
2.
Define \(B_{\mathsf {min}}= \min _{i \in [k]} b_i'(\tau )\), \(B_{\mathsf {max}}= \max _{i \in [k]} b_{i}'(\tau )\), and \(B_{\mathsf {mul}}= \prod _{i \in [k]} b_i'(\tau )\). Set \(r_1 = 1\) and sample \(r_{2}, \ldots , r_{k} {\mathop {\leftarrow }\limits ^{\textsc {r}}}\left[ 4 B_{\mathsf {max}}+ 1, B_{\mathsf {mul}}\cdot 2^{k+2} / \varepsilon ' \right] \). Without loss of generality, we will assume that \(B_{\mathsf {min}}= b_k'(\tau )\).
-
3.
Compute \(\mathsf {st}\leftarrow (\mathsf {st}', b_1'(\tau ), \ldots , b_k'(\tau ), r_1, \ldots , r_k)\), and compute the query vector \(\mathbf {q}\in \mathbb {F}_p^{\ell }\) as
$$\begin{aligned} \mathbf {q}= \sum _{i \in [k]}{\mathbf {q}_{i}'\Bigg (\prod _{j \in [i]}{r_{j}}\Bigg )} \in \mathbb {F}_p^\ell , \end{aligned}$$where \(\mathbf {q}_1', \ldots , \mathbf {q}_k' \in \mathbb {Z}^\ell \) denote the k columns of \(\mathbf {Q}'\).
Output \((\mathsf {st}, \mathbf {q}_{\mathsf {inp}}, \mathbf {q})\).
-
1.
-
\(\mathcal {P}_{\mathsf {LPCP}}(\tau , \mathbf {x}, \mathbf {w})\): On input a statement \(\mathbf {x}\in \mathbb {F}_p^n\) and a witness \(\mathbf {w}\in \mathbb {F}_p^h\), output the proof \(\varvec{\pi }\leftarrow \mathcal {P}_{\mathsf {LPCP}}(\tau , \mathbf {x}, \mathbf {w})\).
-
\(\mathcal {D}_{\mathsf {LPCP}}(\mathsf {st}, a_{\mathsf {inp}}, a)\): On input the state \(\mathsf {st}= (\mathsf {st}', b_1', \ldots , b_k', r_1, \ldots , r_k)\), an input-dependent response \(a_{\mathsf {inp}}\in \mathbb {F}_p\), and a response \(a \in \mathbb {F}_p\), compute \(a_1', \ldots , a_k' \in \mathbb {F}_p\) so that \(a = \sum _{i \in [k]} a_{i}' \prod _{j \in [i]}{r_{j}}\) and each \(a_i'\) satisfies \(a_i' \in [-b_i', b_i']\). This can be done as follows:
-
For each \(i = k, k - 1, \ldots , 1\), compute
 and update \(a \leftarrow a - a_i' \cdot \prod _{j \in [i]} r_j\), where all of these operations happen over the integers (namely, the algorithm interprets the values a and \(a_1', \ldots , a_k'\) as integers in the interval \([-p/2, p/2]\)).
and update \(a \leftarrow a - a_i' \cdot \prod _{j \in [i]} r_j\), where all of these operations happen over the integers (namely, the algorithm interprets the values a and \(a_1', \ldots , a_k'\) as integers in the interval \([-p/2, p/2]\)).
If the above procedure does not produce \(a_1', \ldots , a_k' \in \mathbb {F}_p\) satisfying the above requirements, output 0. Otherwise, output \(\mathcal {D}_{\mathsf {LPCP}}'(\mathsf {st}', a_{\mathsf {inp}}, (a_1', \ldots , a_k'))\).
-
We argue completeness, soundness, and zero-knowledge of Construction 3.2 in the full version of this paper and just state the main corollary below.
Corollary 3.3
(Linear PCP Packing). Let \(\varPi _{\mathsf {LPCP}}'\) be a k-query bounded LPCP over \(\mathbb {F}_p\) for a binary relation \(\mathcal {R}\) with bound functions \(b_1', \ldots , b_k'\), soundness error (resp., strong soundness error) \(\varepsilon '\), and which satisfies \(\delta \)-\(\mathsf {HVZK} \). Let \(B_{\mathsf {min}}' = \min _{i \in [k]} b_i'\), \(B_{\mathsf {mul}}' = \prod _{i \in [k]} b_i'\), and \(B = 2 B_{\mathsf {min}}' \left( B_{\mathsf {mul}}' 2^{k+2} / \varepsilon \right) ^{k-1}\). If \(p > 2B\), then there exists a 1-query bounded LPCP over \(\mathbb {F}_p\) for \(\mathcal {R}\) with bound B, soundness error (resp., strong soundness error) \((k + 1)/2 \varepsilon '\), and which satisfies \(\delta \)-\(\mathsf {HVZK} \).
3.1 Constructing 1-Query Bounded Linear PCPs
As noted in [BCI+13], a simple extension of the Hadamard PCP from [ALM+98, IKO07] to arbitrary finite fields \(\mathbb {F}\) yields a 3-query linear PCP for arithmetic circuit satisfiability over \(\mathbb {F}\). In the full version of this paper, we note that a simple adaptation of the construction yields a 2-query linear PCP. Then, applying our linear PCP packing construction (Corollary 3.3), we obtain the following construction of a 1-query linear PCP:
Corollary 3.4
(1-Query Bounded LPCP). Let  be a Boolean circuit of size s, and let \(\mathbb {F}_p\) be a finite field. Let \(\tau \in \mathbb {N}\) be a bound parameter and \(\delta > 0\) be a zero-knowledge parameter. There exist 1-query bounded linear PCPs over \(\mathbb {F}_p\) for \(\mathcal {R}_C\) with the following properties:
be a Boolean circuit of size s, and let \(\mathbb {F}_p\) be a finite field. Let \(\tau \in \mathbb {N}\) be a bound parameter and \(\delta > 0\) be a zero-knowledge parameter. There exist 1-query bounded linear PCPs over \(\mathbb {F}_p\) for \(\mathcal {R}_C\) with the following properties:
-
Perfect completeness, strong soundness error \(3 / \tau \), query length \((s^2 + 3s) / 2\), and bound function \(b(\tau ) = 4s^4 \tau ^5 / 3\), provided that \(p > 2b(\tau )\); and
-
Perfect completeness, soundness error \(3 / \tau \), query length \((s^2 + 3s) / 2\), \(\delta \)-honest-verifier zero knowledge, and bound function \(b(\tau , \delta ) = 64\tau (s \tau / 2 + 2\tau \sqrt{s/2 \ln (4/\delta )} / \delta )^4 / 3\), provided that \(p > 2b(\tau , \delta )\).
Additionally, the query-generation algorithm \(\mathcal {Q}_{\mathsf {LPCP}}\) and the prover algorithm \(\mathcal {P}_{\mathsf {LPCP}}\) runs in time \(O(s^2) \cdot \mathsf {polylog}(p)\). The verifier’s decision algorithm \(\mathcal {D}_{\mathsf {LPCP}}\) runs in time \(\mathsf {polylog}(p)\).
3.2 SNARGs Based on ElGamal
In this section, we describe how to efficiently compile our 1-query bounded linear PCP from Corollary 3.4 to obtain a designated-verifier SNARG in the preprocessing model where the proof size consists of 2 group elements and where the verification complexity is sublinear in the cost of the classic \(\mathsf {NP} \) verifier. While it is possible to directly invoke the [BCI+13] compiler on our 1-query bounded linear PCP together with ElGamal encryption, the verification complexity of the resulting scheme is quadratic in the size of the classic \(\mathsf {NP} \) verifier. This is because the additively-homomorphic version of ElGamal encryption scheme encodes the messages in the exponent, and decryption requires solving a discrete log. When the responses are bounded in an interval of size B, this can be done in time \(O(\sqrt{B})\) using generic algorithms (e.g., [Pol78]). While a bounded linear PCP seems like a natural choice to use in conjunction with ElGamal, the bounds in Corollary 3.4 scale with \(s^4\), where s is the circuit size of the classic \(\mathsf {NP} \) verifier. Instantiating with ElGamal then yields an unacceptable verification complexity that is quadratic in the circuit size. In this section, we will leverage the structure of our packed 2-query bounded linear PCP to obtain an asymptotically-faster (worst-case verification complexity that scales with \(\widetilde{O}(\sqrt{s})\)) and concretely-efficient designated-verifier SNARG based on ElGamal. Compared with a direct instantiation of the [BCI+13] compiler with ElGamal encryption, our proofs are either 4 times more succinct (2 group elements vs. 8 group elements) or much more concretely efficient (relying on linear PCPs rather than classic PCPs).
The ElGamal instantiation. Before describing how we optimize the verification procedure for our ElGamal-based SNARG, we begin with an explicit description of the construction. We assume a 1-query bounded linear PCP, in which case we obtain a direct construction from any linear-only encryption scheme:
Construction 3.5
(SNARG based on ElGamal). Let  be a Boolean circuit of size s. Let \(\mathsf {GroupGen}\) be a prime-order group generator that outputs a group \(\mathbb {G}\) of prime order p. Let \(\varPi _{\mathsf {LPCP}} = (\mathcal {Q}_{\mathsf {LPCP}}, \mathcal {P}_{\mathsf {LPCP}}, \mathcal {D}_{\mathsf {LPCP}})\) be a 1-query bounded linear PCP with bound \(B = B(\tau )\) and bound parameter \(\tau \) for the relation \(\mathcal {R}_C\) over \(\mathbb {F}_p\). We construct a SNARG \(\varPi _{\mathsf {SNARG}} = (\mathcal {S}_{\mathsf {SNARG}}, \mathcal {P}_{\mathsf {SNARG}}, \mathcal {V}_{\mathsf {SNARG}})\)
be a Boolean circuit of size s. Let \(\mathsf {GroupGen}\) be a prime-order group generator that outputs a group \(\mathbb {G}\) of prime order p. Let \(\varPi _{\mathsf {LPCP}} = (\mathcal {Q}_{\mathsf {LPCP}}, \mathcal {P}_{\mathsf {LPCP}}, \mathcal {D}_{\mathsf {LPCP}})\) be a 1-query bounded linear PCP with bound \(B = B(\tau )\) and bound parameter \(\tau \) for the relation \(\mathcal {R}_C\) over \(\mathbb {F}_p\). We construct a SNARG \(\varPi _{\mathsf {SNARG}} = (\mathcal {S}_{\mathsf {SNARG}}, \mathcal {P}_{\mathsf {SNARG}}, \mathcal {V}_{\mathsf {SNARG}})\)
-
\(\mathcal {S}_{\mathsf {SNARG}}(1^\lambda )\): On input the security parameter \(\lambda \), the setup algorithm samples a group description \((\mathbb {G}, p, g) \leftarrow \mathsf {GroupGen}(1^\lambda )\) and a linear PCP query \((\mathsf {st}', \mathbf {q}_{\mathsf {inp}}, \mathbf {q}) \leftarrow \mathcal {Q}_{\mathsf {LPCP}}(\tau ) \in \mathbb {F}_p^\ell \). The setup algorithm samples a secret key \(\alpha {\mathop {\leftarrow }\limits ^{\textsc {r}}}\mathbb {F}_p\), and computes the ElGamal public key \(h \leftarrow g^\alpha \). The setup algorithm samples \(\mathbf {r}{\mathop {\leftarrow }\limits ^{\textsc {r}}}\mathbb {F}_p^\ell \), and computes the ciphertexts \((g^\mathbf {r}, h^\mathbf {r}g^\mathbf {q})\), where for a vector \(\mathbf {r}\), we write \(g^{\mathbf {r}}\) to denote the vector of group elements \((g^{r_1}, \ldots , g^{r_\ell })\). The setup algorithm outputs the common reference string \(\mathsf {crs}\) and verification state \(\mathsf {st}\):
$$ \mathsf {crs}= \big ( (\mathbb {G}, p, g), h, (g^{\mathbf {r}}, h^{\mathbf {r}} g^{\mathbf {q}}), \tau \big ) \text { and } \mathsf {st}= (\mathsf {st}', \alpha ). $$ -
\(\mathcal {P}_{\mathsf {SNARG}}(\mathsf {crs}, x, w)\): On input a common reference string \(\mathsf {crs}= \big ( (\mathbb {G}, p, g), h,\) \((g^{\mathbf {r}}, g^{\mathbf {s}}), \tau \big )\), a statement
 , and a witness
, and a witness  , the prover algorithm computes a proof \(\varvec{\pi }\leftarrow \mathcal {P}_{\mathsf {LPCP}}(\tau , x, w) \in \mathbb {F}_p^\ell \). It computes the proof as \(\pi = (g^{\mathbf {r}^\mathsf {T}\varvec{\pi }}, g^{\mathbf {s}^\mathsf {T}\varvec{\pi }})\).
, the prover algorithm computes a proof \(\varvec{\pi }\leftarrow \mathcal {P}_{\mathsf {LPCP}}(\tau , x, w) \in \mathbb {F}_p^\ell \). It computes the proof as \(\pi = (g^{\mathbf {r}^\mathsf {T}\varvec{\pi }}, g^{\mathbf {s}^\mathsf {T}\varvec{\pi }})\). -
\(\mathcal {V}_{\mathsf {SNARG}}(\mathsf {st}, x, \pi )\): On input the verification state \(\mathsf {st}= (\mathsf {st}', \mathbf {q}_{\mathsf {inp}}, \alpha )\), the statement
 , and a proof \(\pi = (g_1, g_2)\), the verifier computes \(h' = g_2 / g_1^{\alpha }\), and checks if there exists \(a \in [-B, B]\) such that \(h' = g^a\). It outputs \(\mathcal {D}_{\mathsf {LPCP}}(\mathsf {st}', \mathbf {q}_{\mathsf {inp}}^\mathsf {T}x, a)\).
, and a proof \(\pi = (g_1, g_2)\), the verifier computes \(h' = g_2 / g_1^{\alpha }\), and checks if there exists \(a \in [-B, B]\) such that \(h' = g^a\). It outputs \(\mathcal {D}_{\mathsf {LPCP}}(\mathsf {st}', \mathbf {q}_{\mathsf {inp}}^\mathsf {T}x, a)\).
Assuming that the ElGamal encryption scheme satisfies linear targeted malleability with respect to the target set \([-B, B]\), then Construction 3.5 is a designated-verifier SNARG in the preprocessing model where the proof size consists of exactly 2 group elements. The bottleneck is the expensive verification procedure. As stated, the verification algorithm has to compute the discrete log of \(h' = g^a\) where a is the linear PCP response. This can be computed in time \(\widetilde{O}(\sqrt{B})\), which for the linear PCP from Corollary 3.4, is quadratic in the circuit size s.
Optimizing the verification procedure. We now describe how to more efficiently implement the verification procedure in Construction 3.5 to obtain a SNARG whose worst-case verification complexity is O(s). Moreover, if we allow for a negligible completeness error (as opposed to perfect completeness), we give a procedure whose worst-case verification complexity is \(\widetilde{O}(\sqrt{s})\). Our optimization will rely on specific properties of the linear PCP from Corollary 3.4. Namely, the 1-query linear PCP from Corollary 3.4 was obtained by packing together a 2-query linear PCP.
-
The 2-query linear PCP has the property that the verifier accepts a response \((a_1, a_2) \in \mathbb {F}_p^2\) only if \(a_1^2 + a_2 = a_{\mathsf {inp}}+ u_C\), where \(a_{\mathsf {inp}}, u_C \in \mathbb {F}_p\) are scalars that are known to the verifier.
-
If \(\mathbf {q}_1, \mathbf {q}_2 \in \mathbb {F}_p^\ell \) are the two queries the verifier makes, then the packed query in Construction 3.2 satisfies \(\mathbf {q}= \mathbf {q}_1 + r \cdot \mathbf {q}_2\) for some \(r \in \mathbb {F}_p\) known to the verifier. This means that the honest prover’s response satisfies \(a = \mathbf {q}^\mathsf {T}\varvec{\pi }= \mathbf {q}_1^\mathsf {T}\varvec{\pi }+ r \cdot \mathbf {q}_2^\mathsf {T}\varvec{\pi }= a_1 + r \cdot a_2\).
-
Finally, for an accepting proof, the first response \(a_1\) satisfies \(a_1 \in [-b_1(\tau ), b_1(\tau )] = [-s \tau / 2, s \tau / 2]\).
Equivalently, this means the linear PCP verifier accepts only if there exists \(a_1 \in [-b_1(\tau ), b_1(\tau )]\) such that the following two relations hold:
or equivalently, if there exists \(a_1 \in [-b_1(\tau ), b_1(\tau )]\) such that
In the SNARG from Construction 3.5, the verifier first computes \(g^a\). Now, instead of recovering a by solving discrete log, the verifier instead checks whether there exists \(a_1 \in [-b_1(\tau ), b_1(\tau )]\) where
This can be done by performing a brute force search over all of the possible \(2 b_1(\tau )\) values for \(a_1\) and seeing if Eq. (3.2) holds. We can also rewrite Eq. (3.2) as checking whether there exists \(a_1\) where
Observe now that the right-hand side of the expression depends only on the value of \(a_1\) and r, and in particular, is independent of the statement. Since r is sampled by the setup algorithm \(\mathcal {S}_{\mathsf {SNARG}}\), the verifier can actually precompute a table of values \(g^{a_1 - r a_1^2}\) for each possible value of \(a_1\). Then, to verify a proof \(\pi = (g_1, g_2)\), the verifier computes \(u = g^a g^{-r (a_\mathsf {inp} + u_C)}\), which requires a constant number of group operations, and finally, checks to see whether u is contained in the table or not. This yields a substantially faster verification procedure. Even without this optimization, we obtain a SNARG where the verification complexity is O(s). We summarize this in the following corollary:
Corollary 3.6
(SNARG from ElGamal with Perfect Completeness). Let  be a Boolean circuit of size s. Let \(\varepsilon > 0\) be a soundness parameter and \(\delta > 0\) be a zero-knowledge parameter. Assuming the ElGamal encryption scheme (over a prime order group \(\mathbb {G}\) of order p) satisfies linear targeted malleability with respect to a target message space \([-B, B]\) for \(B = \mathsf {poly} (s, 1 / \varepsilon , 1 / \delta )\), there exist a designated-verifier SNARGs for \(\mathcal {R}_C\) with perfect completeness, non-adaptive soundness error \(\varepsilon \), and proofs of size
be a Boolean circuit of size s. Let \(\varepsilon > 0\) be a soundness parameter and \(\delta > 0\) be a zero-knowledge parameter. Assuming the ElGamal encryption scheme (over a prime order group \(\mathbb {G}\) of order p) satisfies linear targeted malleability with respect to a target message space \([-B, B]\) for \(B = \mathsf {poly} (s, 1 / \varepsilon , 1 / \delta )\), there exist a designated-verifier SNARGs for \(\mathcal {R}_C\) with perfect completeness, non-adaptive soundness error \(\varepsilon \), and proofs of size  . The CRS has size \(O(s^2)\). The setup algorithm and prover run in time \(O(s^2)\) and the verifier runs in time \(O(s / \varepsilon )\). Moreover, the SNARG can be extended to satisfy \(\delta \)-\(\mathsf {HVZK} \). In this case, the verifier runs in time \(O(\sqrt{s} / \varepsilon \cdot (\sqrt{s} + \sqrt{\log (1 / \delta )} / \delta ))\); the setup and prover complexity remain unchanged. All of the running times are up to \(\mathsf {polylog}(p)\) factors.
. The CRS has size \(O(s^2)\). The setup algorithm and prover run in time \(O(s^2)\) and the verifier runs in time \(O(s / \varepsilon )\). Moreover, the SNARG can be extended to satisfy \(\delta \)-\(\mathsf {HVZK} \). In this case, the verifier runs in time \(O(\sqrt{s} / \varepsilon \cdot (\sqrt{s} + \sqrt{\log (1 / \delta )} / \delta ))\); the setup and prover complexity remain unchanged. All of the running times are up to \(\mathsf {polylog}(p)\) factors.
Sublinear verification. We can further reduce the verification complexity by having the verifier only accept proofs where the first response \(a_1\) is contained in a much shorter interval. In the full version of this paper, we show that with overwhelming probability, \(a_1 \in [-b_1'(\tau ), b_1'(\tau )]\) where \(b_1'(\tau ) = \widetilde{O}(\tau \sqrt{s})\). We now modify the verification procedure \(\mathcal {V}_{\mathsf {SNARG}}\) to only accept if there exists \(a_1 \in [-b_1'(\tau ), b_1'(\tau )]\) such that Eq. (3.3) holds. Since the subset of proofs the verifier accepts is now a strict subset of the proofs it accepted in the original scheme, (single-theorem) soundness is preserved. The trade-off is that the verifier may now reject some honestly-generated proofs, but this can only happen with negligible probability over the verifier’s randomness. This yields the following theorem:
Corollary 3.7
(SNARG from ElGamal with Sublinear Verification). Let  be a Boolean circuit of size s. Let \(\varepsilon > 0\) be a soundness parameter and \(\delta > 0\) be a zero-knowledge parameter. Assuming the ElGamal encryption scheme (over a prime order group \(\mathbb {G}\) of order p) satisfies linear targeted malleability with respect to a target message space \([-B, B]\) for \(B = \mathsf {poly} (s, 1 / \varepsilon , 1 / \delta )\), there exists a designated-verifier SNARG for \(\mathcal {R}_C\) with statistical completeness and non-adaptive soundness error \(\varepsilon \), and proofs of size
be a Boolean circuit of size s. Let \(\varepsilon > 0\) be a soundness parameter and \(\delta > 0\) be a zero-knowledge parameter. Assuming the ElGamal encryption scheme (over a prime order group \(\mathbb {G}\) of order p) satisfies linear targeted malleability with respect to a target message space \([-B, B]\) for \(B = \mathsf {poly} (s, 1 / \varepsilon , 1 / \delta )\), there exists a designated-verifier SNARG for \(\mathcal {R}_C\) with statistical completeness and non-adaptive soundness error \(\varepsilon \), and proofs of size  . The CRS has size \(O(s^2)\). The setup algorithm and prover run in time \(O(s^2)\) and the verifier runs in time \(\widetilde{O}(\sqrt{s} / \varepsilon )\). Moreover, the SNARG can be extended to satisfy \(\delta \)-\(\mathsf {HVZK} \). In this case, the verifier runs in time \(\widetilde{O}(\sqrt{s \log (1 / \delta )} / (\delta \varepsilon ))\); the setup and prover complexity remain unchanged. All of the running times are up to \(\mathsf {polylog}(p)\) factors.
. The CRS has size \(O(s^2)\). The setup algorithm and prover run in time \(O(s^2)\) and the verifier runs in time \(\widetilde{O}(\sqrt{s} / \varepsilon )\). Moreover, the SNARG can be extended to satisfy \(\delta \)-\(\mathsf {HVZK} \). In this case, the verifier runs in time \(\widetilde{O}(\sqrt{s \log (1 / \delta )} / (\delta \varepsilon ))\); the setup and prover complexity remain unchanged. All of the running times are up to \(\mathsf {polylog}(p)\) factors.
A preprocessing variant. As mentioned above, the verification relation in Eq. (3.3) is very amenable to preprocessing. Namely, the verifier can perform a one-time setup and precompute all of the accepting values of \(g^{a_1 - r a_1^2}\) and store them in a table. Applying the sublinear verification approach described above, this will only require \(\widetilde{O}(\sqrt{s})\) space when verifying circuits of size s. In the online phase, to check a proof, the verifier needs to perform a single ElGamal decryption, followed by computing the left-hand side of Eq. (3.3), and finally, a single table lookup. The overall computation comes out to just 2 exponentiations and 2 multiplications, followed by the table lookup. This yields the following corollary:
Corollary 3.8
(SNARG from ElGamal with Preprocessing). Let  be a Boolean circuit of size s. Let \(\varepsilon > 0\) be a soundness parameter and \(\delta > 0\) be a zero-knowledge parameter. Assuming the ElGamal encryption scheme (over a prime order group \(\mathbb {G}\) of order p) satisfies linear targeted malleability with respect to a target message space \([-B, B]\) for \(B = \mathsf {poly} (s, 1 / \varepsilon , 1 / \delta )\), there exists a designated-verifier SNARG for \(\mathcal {R}_C\) with statistical completeness, non-adaptive soundness error \(\varepsilon \), and proofs of size
be a Boolean circuit of size s. Let \(\varepsilon > 0\) be a soundness parameter and \(\delta > 0\) be a zero-knowledge parameter. Assuming the ElGamal encryption scheme (over a prime order group \(\mathbb {G}\) of order p) satisfies linear targeted malleability with respect to a target message space \([-B, B]\) for \(B = \mathsf {poly} (s, 1 / \varepsilon , 1 / \delta )\), there exists a designated-verifier SNARG for \(\mathcal {R}_C\) with statistical completeness, non-adaptive soundness error \(\varepsilon \), and proofs of size  . The CRS has size \(O(s^2)\). The setup algorithm runs in time \(\widetilde{O}(s^2 + \sqrt{s} / \varepsilon )\) and outputs a table \(\mathsf {T}\) of size \(\widetilde{O}(\sqrt{s} / \varepsilon )\). The prover runs in time \(O(s^2)\) and the verifier runs in time \(\widetilde{O}(1)\) given access to the precomputed table \(\mathsf {T}\). If we extend the SNARG to provide \(\delta \)-\(\mathsf {HVZK} \), the setup algorithm now runs in time \(O(s^2 + \sqrt{s \log (1 / \delta )}/(\delta \varepsilon ))\) and outputs a table \(\mathsf {T}\) of size \(O(\sqrt{s \log (1 / \delta )}/(\delta \varepsilon ))\). Given access to the precomputed table, the verifier’s runtime is \(\widetilde{O}(1)\). All of the running times and table sizes are up to \(\mathsf {polylog}(p)\) factors.
. The CRS has size \(O(s^2)\). The setup algorithm runs in time \(\widetilde{O}(s^2 + \sqrt{s} / \varepsilon )\) and outputs a table \(\mathsf {T}\) of size \(\widetilde{O}(\sqrt{s} / \varepsilon )\). The prover runs in time \(O(s^2)\) and the verifier runs in time \(\widetilde{O}(1)\) given access to the precomputed table \(\mathsf {T}\). If we extend the SNARG to provide \(\delta \)-\(\mathsf {HVZK} \), the setup algorithm now runs in time \(O(s^2 + \sqrt{s \log (1 / \delta )}/(\delta \varepsilon ))\) and outputs a table \(\mathsf {T}\) of size \(O(\sqrt{s \log (1 / \delta )}/(\delta \varepsilon ))\). Given access to the precomputed table, the verifier’s runtime is \(\widetilde{O}(1)\). All of the running times and table sizes are up to \(\mathsf {polylog}(p)\) factors.
Remark 3.9
(Arguments of Knowledge). The SNARG constructions in Corollaries 3.6 to 3.8 are all arguments of knowledge (i.e., “SNARKs”) since the underlying linear PCPs provide knowledge soundness and Construction 3.2 preserves the knowledge soundness of the underlying linear PCP.
3.3 Concrete Efficiency of the ElGamal-Based SNARG
In the full version of this paper, we provide an overview of our methodology for estimating the concrete efficient of our ElGamal-based SNARG. A summary of the main results is provided in Table 2.
4 1-Query Linear PCP from Hardness of Approximation
In the full version of this paper, we show how to construct a 1-query instance-dependent linear PCP with a linear decision procedure and negligible soundness error. Combined with the compiler from [BCI+13], and assuming linear targeted malleability of ElGamal encryption, we obtain the first laconic argument with negligible soundness error where the proof consists of a single ElGamal ciphertext. Note that we do not obtain a SNARG because the verifier’s first message (i.e., the verifier’s query) depends on the statement. We refer to Sect. 1.2 for a high-level overview of the construction.
5 1-Element Laconic Arguments and Witness Encryption
In the full version of this paper, we show that any laconic argument system for an \(\mathsf {NP} \) language \(\mathcal {L}\) (with negligible soundness error) where the proof consists of a single group element (i.e., a “1-element laconic argument”) and where the verification algorithm can be modeled as a “generic” algorithm implies a witness encryption scheme for \(\mathcal {L}\). Note that since the prover is restricted to sending a single group element, this effectively restricts the prover to sending at most one message in the protocol. Thus, it suffices to just consider 2-message laconic arguments here. Our construction of witness encryption proceeds in two steps. We first show that any laconic argument satisfying the above properties must be predictable [FNV17]. We then invoke the Faonio et al. [FNV17] compiler on the predictable argument to obtain a witness encryption scheme.
Next, we show that under a new hypothesis on the hardness of approximating the minimum distance of a linear code [DMS99] (Hypothesis 5.2), we can construct a laconic element for \(\mathsf {NP} \) where the proof consists of a single group element in the generic group model. Thus, under our hypothesis, we obtain a witness encryption scheme for \(\mathsf {NP} \) in the generic group model.
5.1 1-Element Laconic Argument from Hardness of Approximation
In this section, we show that under a hardness of approximation hypothesis for the minimum distance problem [DMS99], we can construct a 1-element laconic argument for general \(\mathsf {NP} \) languages. We begin by recalling the minimum distance problem and then stating our hardness of approximation hypothesis.
Definition 5.1
(Gap Minimum Distance Problem (\(\mathsf {GapMDP} \)) [DMS99, Definition 1]). For an approximation factor \(\beta \), an instance of \(\mathsf {GapMDP} _\beta \) is a pair \((\mathbf {A}, d)\) where \(\mathbf {A}\in \mathbb {F}^{n \times k}\) for some finite field \(\mathbb {F}\) and \(d \in \mathbb {N}\) such that
-
\((\mathbf {A}, d)\) is a yes instance if \(\mathsf {dist} (\mathbf {A}) \le d\).
-
\((\mathbf {A}, d)\) is a no instance if \(\mathsf {dist} (\mathbf {A}) \ge \beta \cdot d\).
Here, \(\mathsf {dist} (\mathbf {A})\) is the minimum distance (under the Hamming metric) of the code generated by \(\mathbf {A}\). A witness for a \(\textsc {yes} \) instance \((\mathbf {A}, d)\) is a nonzero codeword \(\mathbf {0}\ne \mathbf {v}\in \mathbb {F}^k\) (in the code generated by \(\mathbf {A}\)) where \(\mathsf {wt}(\mathbf {v}) \le d\).
Hypothesis 5.2
(Hardness of Approximation for \(\mathsf {GapMDP} \)). For some \(\beta = \omega (\log n)\), the \(\mathsf {GapMDP} _\beta \) problem is \(\mathsf {NP}\text {-}\mathsf {hard} \) for any choice of finite field \(\mathbb {F}\) where  . Specifically, there exists a deterministic Karp-Levin reduction from \(\mathsf {SAT} \) to \(\mathsf {GapMDP} _\beta \), where the reduction algorithm takes a target field \(\mathbb {F}\) as an explicit input and outputs an instance \((\mathbf {A}, d)\) over \(\mathbb {F}\) in time
. Specifically, there exists a deterministic Karp-Levin reduction from \(\mathsf {SAT} \) to \(\mathsf {GapMDP} _\beta \), where the reduction algorithm takes a target field \(\mathbb {F}\) as an explicit input and outputs an instance \((\mathbf {A}, d)\) over \(\mathbb {F}\) in time  .
.
Existing hardness results on \(\mathsf {GapMDP} \). Dumer et al. [DMS99] showed that the \(\mathsf {GapMDP} \) was \(\mathsf {NP}\text {-}\mathsf {hard} \) for any constant approximation factor \(\beta = O(1)\) (over any polynomial-size field) via a randomized reduction. Subsequently, Cheng and Wan [CW09] as well as Austrin and Khot [AK14] gave a deterministic reduction for the same parameter regimes. The latter results additionally give a deterministic quasi-polynomial time reduction from \(\mathsf {NP} \) to the \(\mathsf {GapMDP} _\beta \) for any \(\beta = 2^{\log ^{1-\varepsilon }(n)}\) (i.e., unless \(\mathsf {NP} \subseteq \mathsf {DTIME} (2^{\mathsf {polylog}(n)})\), there is no polynomial-time algorithm for \(\mathsf {GapMDP} _\beta \)). In our setting, we need to strengthen the existing hardness of approximation results in two different directions: (1) Hypothesis 5.2 requires a deterministic polynomial time reduction to \(\mathsf {GapMDP} \) while the existing reductions in the super-constant regime are all quasi-polynomial; and (2) we require that the reduction applies to large prime characteristic fields (i.e., fields that are super-polynomial in the instance size). While existing reductions are agnostic about the choice of the field, the running time of existing reductions scale polynomially in the characteristic of the field, so they do not directly generalize to super-polynomial size fields.Footnote 10 While existing techniques do not suffice for proving Hypothesis 5.2, there are no known barriers to doing so [Kho20]
Construction 5.3
(Laconic Argument for \(\mathsf {GapMDP} \)). Let \(\lambda \) be a security parameter, \(\varepsilon > 0\) be a completeness parameter, and \(\beta > 0\) be the approximation factor. Let \(\mathsf {GroupGen}\) be a prime-order group generator, and let \(p = p(\lambda )\) be the order of the group output by \(\mathsf {GroupGen}\). We construct a two-message laconic argument \(\varPi _{\mathsf {LA}} = (\mathcal {Q}_{\mathsf {LA}}, \mathcal {P}_{\mathsf {LA}}, \mathcal {V}_{\mathsf {LA}})\) for \(\mathsf {GapMDP} _\beta \) (for instances over \(\mathbb {F}_p\)):
-
\(\mathcal {Q}_{\mathsf {LA}}(1^{\lambda }, (\mathbf {A}, d))\): On input the security parameter \(\lambda \) and an \(\mathsf {GapMDP} _\beta \) instance \((\mathbf {A}, d)\) over \(\mathbb {F}_p\), the query algorithm samples \((\mathbb {G}, p, g) \leftarrow \mathsf {GroupGen}(1^\lambda )\). Let \(\mathbf {H}\in \mathbb {F}_p^{\ell \times k}\) be the parity check matrix for the code generated by \(\mathbf {A}\). Then the verifier constructs the following components:
-
Sample a random vector \(\mathbf {e}\in \mathbb {F}_p^k\) where each component \(e_i = 0\) with probability \(1 - \varepsilon / d\) and \(e_i {\mathop {\leftarrow }\limits ^{\textsc {r}}}\mathbb {F}_p\) otherwise.
-
Sample \(\mathbf {c}{\mathop {\leftarrow }\limits ^{\textsc {r}}}\mathbb {F}_p^k\), \(\mathbf {r}{\mathop {\leftarrow }\limits ^{\textsc {r}}}\mathbb {F}_p^\ell \), \(s {\mathop {\leftarrow }\limits ^{\textsc {r}}}\mathbb {F}_p\) and compute \(\mathbf {z}^\mathsf {T}= \mathbf {r}^\mathsf {T}\mathbf {H}+ s \mathbf {c}^\mathsf {T}+ \mathbf {e}^\mathsf {T}\in \mathbb {F}_p^k\).
The algorithm outputs \(((\mathbb {G}, p, g), \mathbf {c}, g^{\mathbf {z}})\) as its query and \(\mathsf {st}= g^{s}\) as its state. Here, we write \(g^{\mathbf {z}}\) to denote the vector of group elements \((g^{z_1}, \ldots , g^{z_k})\), where \(z_1, \ldots , z_k\) are the components of \(\mathbf {z}\).
-
-
\(\mathcal {P}_{\mathsf {LA}}(q, x, w)\): On input a query \(q = ((\mathbb {G}, p, g), \mathbf {c}, g^{\mathbf {z}})\), a \(\mathsf {GapMDP} \) instance \((\mathbf {A}, d)\) and a witness \(\mathbf {v}\in \mathbb {F}_p^k\), the prover algorithm does the following:
-
If \(\mathbf {c}^\mathsf {T}\mathbf {v}= 0\), then the prover aborts with output \(\bot \). Otherwise, let \(t = (\mathbf {c}^\mathsf {T}\mathbf {v})^{-1}\).
-
Output the proof \(\pi = g^{t \cdot \mathbf {z}^\mathsf {T}\mathbf {v}}\) (which can be computed from t, \(\mathbf {v}\), and \(g^{\mathbf {z}}\)).
-
-
\(\mathcal {V}_{\mathsf {LA}}(\mathsf {st}, \pi )\): On input the verification state \(\mathsf {st}\in \mathbb {G}\) and a proof \(\pi \in \mathbb {G}\), output 1 if \(\mathsf {st}= \pi \), and 0 otherwise.
Completeness and soundness analysis. We now state the completeness and soundness theorems for Construction 5.3 as well as the resulting implication to 1-element laconic arguments and witness encryption for \(\mathsf {NP} \) in the generic group model. We defer the completeness and soundness proofs to the full version of this paper.
Theorem 5.4
(Completeness). Construction 5.3 has completeness error \(\varepsilon \).
Theorem 5.5
(Soundness). If \(\varepsilon \beta = \omega (\log n)\) and \(\mathsf {GroupGen}\) is modeled as a generic group, then Construction 5.3 has soundness error \(\mathsf {negl} (\lambda )\).
Corollary 5.6
(1-Element Laconic Argument for \(\mathsf {NP} \)). Let \(\lambda \) be a security parameter. Under Hypothesis 5.2, there exists a predictable laconic argument for \(\mathsf {NP} \) in the generic group model with completeness error o(1) and soundness error \(\mathsf {negl} (\lambda )\) and where the prover’s message consists of a single group element.
Proof
Let \(\beta (\lambda ) = f(\lambda ) \log \lambda \) where \(f(\lambda ) = \omega (1)\) for which Hypothesis 5.2 holds. Take \(\varepsilon = 1 / \sqrt{f(\lambda )} = o(1)\). By instantiating Construction 5.3 with this choice of \(\beta , \varepsilon \) and appealing to Theorems 5.4 and 5.5, we obtain a laconic argument for \(\mathsf {GapMDP} _\beta \) with completeness error \(\varepsilon = o(1)\) and soundness error \(\mathsf {negl} (\lambda )\). In addition, Construction 5.3 is predictable by construction. Finally, by Hypothesis 5.2, there exists a deterministic polynomial-time Karp-Levin reduction from \(\mathsf {NP} \) to \(\mathsf {GapMDP} _\beta \), and so we can use our laconic argument for \(\mathsf {GapMDP} _\beta \) to obtain a laconic argument for any \(\mathsf {NP} \) language.
Corollary 5.7
(Hypothetical Witness Encryption for \(\mathsf {NP} \) in the Generic Group Model). Under Hypothesis 5.2, there exists a witness encryption scheme for \(\mathsf {NP} \) in the generic group model.
Proof
Follows by instantiating the general compiler from [FNV17] with the predictable laconic argument from Corollary 5.6. We provide more details in the full version of this paper.
Notes
- 1.
As we discuss in greater detail in Sect. 1.1, our constructions naturally extend via standard techniques to provide zero-knowledge and arguments of knowledge (namely, they are “zkSNARKs”). For simplicity of exposition, we just focus on SNARGs here.
- 2.
- 3.
Technically, a weaker property called linear targeted malleability [BSW12] suffices for a basic version of the compiler. For ease of exposition, we present everything here using the concept of linear-only encryption. We formally define linear targeted malleability in the full version of this paper.
- 4.
Indeed, by flipping one bit of an honestly-generated PCP, a malicious prover can mount a selective failure attack that makes the verifier reject with high probability if this bit is being queried.
- 5.
While we present the general ideas using linear PCPs over the integers, the construction in Sect. 3 embeds the integer operations over a large finite field \(\mathbb {F}_p\).
- 6.
If the packing transformation requires the use of a larger field than that of the underlying linear PCP, this can negate the benefit of the packing.
- 7.
In a witness encryption scheme [GGSW13], the prover can encrypt a message to an \(\mathsf {NP} \) statement x such that anyone with knowledge of the witness w is able to decrypt and recover the message. This is a very powerful notion of encryption whose only instantiations rely on conjectures related to indistinguishability obfuscation [GGH+13], multilinear maps [GGSW13, GLW14, CVW18], or new and relatively unexplored algebraic structures [BIJ+20].
- 8.
We can also define integer linear PCPs for an (infinite) family of relations \(\mathcal {R}= \bigcup _{\kappa \in \mathbb {N}} \mathcal {R}_\kappa \). In this case, the inputs to the query-generation and proving algorithms would additionally take the relation index \(1^\kappa \) as input, and the parameters \(n, h, k, \ell , B, \varepsilon \) can all be functions of \(\kappa \).
- 9.
We can consider a stronger notion of zero-knowledge where the simulator does not have access to the statement \(\mathbf {x}\). This is the setting considered in fully linear PCPs [BBC+19] and has applications to constructing proofs on committed values or secret-shared values. This stronger notion can also be relevant in our setting where a verifier is checking proofs from multiple provers (who may each hold a secret share of a distributed database), and the goal is to minimize proof size or verifier complexity.
- 10.
We formulate the hypothesis for
 , although any field of super-polynomial size would also suffice.
, although any field of super-polynomial size would also suffice.
References
Austrin, P., Khot, S.: A simple deterministic reduction for the gap minimum distance of code problem. IEEE Trans. Inf. Theory 60(10), 6636–6645 (2014)
Aumann, Y., Lindell, Y.: Security against covert adversaries: efficient protocols for realistic adversaries. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 137–156. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_8
Arora, S., Lund, C., Motwani, R., Sudan, M., Szegedy, M.: Proof verification and the hardness of approximation problems. J. ACM 45(3), 501–555 (1998)
Bünz, B., Bootle, J., Boneh, D., Poelstra, A., Wuille, P., Maxwell, G.: Bulletproofs: short proofs for confidential transactions and more. In: IEEE SP (2018)
Boneh, D., Boyle, E., Corrigan-Gibbs, H., Gilboa, N., Ishai, Y.: Zero-knowledge proofs on secret-shared data via fully linear PCPs. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 67–97. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_3
Backes, M., Barbosa, M., Fiore, D., Reischuk, R.M.: ADSNARK: nearly practical and privacy-preserving proofs on authenticated data. In: IEEE SP (2015)
Ben-Sasson, E., Bentov, I., Horesh, Y., Riabzev, M.: Scalable zero knowledge with no trusted setup. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 701–732. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_23
Bitansky, N., Chiesa, A.: Succinct arguments from multi-prover interactive proofs and their efficiency benefits. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 255–272. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_16
Brassard, G., Chaum, D., Crépeau, C.: Minimum disclosure proofs of knowledge. J. Comput. Syst. Sci. 37(2), 156–189 (1988)
Bootle, J., Cerulli, A., Chaidos, P., Groth, J., Petit, C.: Efficient zero-knowledge arguments for arithmetic circuits in the discrete log setting. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 327–357. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_12
Bitansky, N., et al.: The hunting of the SNARK. J. Cryptol. 30(4), 989–1066 (2017)
Bitansky, N., Canetti, R., Chiesa, A., Tromer, E.: From extractable collision resistance to succinct non-interactive arguments of knowledge, and back again. In: ITCS (2012)
Ben-Sasson, E., Chiesa, A., Genkin, D., Tromer, E., Virza, M.: SNARKs for C: verifying program executions succinctly and in zero knowledge. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 90–108. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_6
Ben-Sasson, E., et al.: Zerocash: decentralized anonymous payments from bitcoin. In: IEEE SP (2014)
Bitansky, N., Chiesa, A., Ishai, Y., Paneth, O., Ostrovsky, R.: Succinct non-interactive arguments via linear interactive proofs. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 315–333. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_18
Berman, I., Degwekar, A., Rothblum, R.D., Vasudevan, P.N.: From laconic zero-knowledge to public-key cryptography. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 674–697. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_23
Bernstein, D.J.: Curve25519: new Diffie-Hellman speed records. In: Yung, M., Dodis, Y., Kiayias, A., Malkin, T. (eds.) PKC 2006. LNCS, vol. 3958, pp. 207–228. Springer, Heidelberg (2006). https://doi.org/10.1007/11745853_14
Boppana, R.B., Håstad, J., Zachos, S.: Does co-NP have short interactive proofs? Inf. Process. Lett. 25(2), 127–132 (1987)
Bartusek, J., Ishai, Y., Jain, A., Ma, F., Sahai, A., Zhandry, M.: Affine determinant programs: a framework for obfuscation and witness encryption. In: ITCS (2020)
Boneh, D., Ishai, Y., Sahai, A., Wu, D.J.: Lattice-based SNARGs and their application to more efficient obfuscation. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 247–277. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_9
Boneh, D., Ishai, Y., Sahai, A., Wu, D.J.: Quasi-optimal SNARGs via linear multi-prover interactive proofs. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 222–255. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_8
Boneh, D., Segev, G., Waters, B.: Targeted malleability: homomorphic encryption for restricted computations. In: ITCS (2012)
Di Crescenzo, G., Lipmaa, H.: Succinct NP Proofs from an extractability assumption. In: Beckmann, A., Dimitracopoulos, C., Löwe, B. (eds.) CiE 2008. LNCS, vol. 5028, pp. 175–185. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-69407-6_21
Canetti, R., Ostrovsky, R.: Secure computation with honest-looking parties: what if nobody is truly honest? In: STOC (1999)
Chen, Y., Vaikuntanathan, V., Wee, H.: GGH15 beyond permutation branching programs: proofs, attacks, and candidates. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 577–607. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_20
Cheng, Q., Wan, D.: A deterministic reduction for the gap minimum distance problem: [extended abstract]. In: STOC (2009)
Danezis, G., Fournet, C., Groth, J., Kohlweiss, M.: Square span programs with applications to succinct NIZK arguments. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 532–550. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_28
Dumer, I., Micciancio, D., Sudan, M.: Hardness of approximating the minimum distance of a linear code. In: FOCS (1999)
ElGamal, T.: A public key cryptosystem and a signature scheme based on discrete logarithms. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 10–18. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_2
Faonio, A., Nielsen, J.B., Venturi, D.: Predictable arguments of knowledge. In: PKC (2017)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS (2013)
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_37
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In: STOC (2013)
Goldreich, O., Håstad, J.: On the complexity of interactive proofs with bounded communication. Inf. Process. Lett. 67(4), 205–214 (1998)
Gentry, C., Lewko, A., Waters, B.: Witness encryption from instance independent assumptions. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 426–443. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_24
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof-systems (extended abstract). In: STOC (1985)
Goldreich, O.: Candidate one-way functions based on expander graphs. Electron. Colloquium Comput. Complex. (ECCC) 7(90) (2000)
Groth, J.: Short pairing-based non-interactive zero-knowledge arguments. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 321–340. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_19
Groth, J.: On the size of pairing-based non-interactive arguments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 305–326. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_11
Goldreich, O., Vadhan, S., Wigderson, A.: On interactive proofs with a laconic prover. In: Orejas, F., Spirakis, P.G., van Leeuwen, J. (eds.) ICALP 2001. LNCS, vol. 2076, pp. 334–345. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-48224-5_28
Gentry, C., Wichs, D.: Separating succinct non-interactive arguments from all falsifiable assumptions. In: STOC (2011)
Ishai, Y., Kushilevitz, E., Ostrovsky, R.: Efficient arguments without short PCPs. In: CCC (2007)
Khot, S.: Personal communication (2020)
Kilian, J.: A note on efficient zero-knowledge proofs and arguments. In: STOC (1992)
Kilian, J., Micali, S., Ostrovsky, R.: Minimum resource zero-knowledge proofs. In: FOCS (1989)
Khot, S., Popat, P., Vishnoi, N.K.: 2\(^{\text{log1-}\varepsilon \,\,{n}}\) hardness for the closest vector problem with preprocessing. In: STOC (2012)
Lipmaa, H.: Progression-free sets and sublinear pairing-based non-interactive zero-knowledge arguments. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 169–189. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_10
Micali, S.: Computationally sound proofs. SIAM J. Comput. 30(4), 1253–1298 (2000)
Mie, T.: Polylogarithmic two-round argument systems. J. Math. Cryptol. 2(4), 343–363 (2008)
Mahmoody, M., Mohammed, A., Nematihaji, S., Pass, R., Shelat, A.: Lower bounds on assumptions behind indistinguishability obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 49–66. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_3
Mahmoody, M., Mohammed, A., Nematihaji, S., Pass, R., Shelat, A.: A note on black-box complexity of indistinguishability obfuscation. IACR Cryptol. ePrint Arch., 2016, 316 (2016)
Nechaev, V.I.: Complexity of a determinate algorithm for the discrete logarithm. Math. Notes 55, 165–172 (1994)
Parno, B., Howell, J., Gentry, C., Raykova, M.: Pinocchio: nearly practical verifiable computation. In: IEEE SP (2013)
Pollard, J.M.: Monte carlo methods for index computation (mod p). Math. Comput. 32(143), 918–924 (1978)
Papakonstantinou, P.A., Rackoff, C., Vahlis, Y.: How powerful are the DDH hard groups? IACR Cryptol. ePrint Arch., 2012 (2012)
Raz, R.: A parallel repetition theorem. In: STOC, pp. 447–456 (1995)
SCIPR Lab. libsnark: a C++ library for zkSNARK proofs (2020). https://github.com/scipr-lab/libsnark
Shoup, V.: Lower bounds for discrete logarithms and related problems. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 256–266. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_18
Wee, H.: On round-efficient argument systems. In: Caires, L., Italiano, G.F., Monteiro, L., Palamidessi, C., Yung, M. (eds.) ICALP 2005. LNCS, vol. 3580, pp. 140–152. Springer, Heidelberg (2005). https://doi.org/10.1007/11523468_12
Acknowledgments
We thank Henry Corrigan-Gibbs, Subhash Khot, and Sam Kim for insightful discussions and pointers. We thank the anonymous reviewers for helpful feedback on the presentation.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Barta, O., Ishai, Y., Ostrovsky, R., Wu, D.J. (2020). On Succinct Arguments and Witness Encryption from Groups. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12170. Springer, Cham. https://doi.org/10.1007/978-3-030-56784-2_26
Download citation
DOI: https://doi.org/10.1007/978-3-030-56784-2_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56783-5
Online ISBN: 978-3-030-56784-2
eBook Packages: Computer ScienceComputer Science (R0)


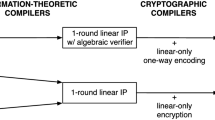

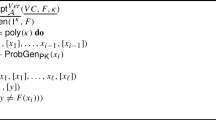
 .
.
 and update
and update  , and a witness
, and a witness  , the prover algorithm computes a proof
, the prover algorithm computes a proof  , and a proof
, and a proof  , although any field of super-polynomial size would also suffice.
, although any field of super-polynomial size would also suffice.