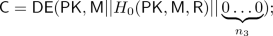Abstract
We initiate the study of indifferentiability for public key encryption and other public key primitives. Our main results are definitions and constructions of public key cryptosystems that are indifferentiable from ideal cryptosystems, in the random oracle model. Cryptosystems include:
-
Public key encryption;
-
Digital signatures;
-
Non-interactive key agreement.
Our schemes are based on relatively standard public key assumptions. By being indifferentiable from an ideal object, our schemes automatically satisfy a wide range of security properties, including any property representable as a single-stage game, and can be composed to operate in higher-level protocols.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
When designing a cryptographic system, it is difficult to predict how it will be used in practice and what security properties will be required of it. For example, if the larger system produces certain error messages, this can lead to chosen ciphertext attacks [6]. Perhaps a message is encrypted using random coins which themselves are derived from the message, as is used for de-duplication [28]. Maybe the secret key itself will be encrypted by the system, as is sometimes used in disk encryption. Or perhaps there was bad randomness generation on the hardware device, leading to secret keys or encryption randomness that is low-entropy or correlated across many instances.
Cryptographers have devised different security models to capture each of the scenarios above and more, each requiring different constructions to satisfy. However, seldom are these different security models considered in tandem, meaning that each application scenario may require a different scheme. Even worse, there are many potential security models that have yet to be considered; after all, it is difficult to predict the various applications devised by software developers that may deviate from the existing provably secure uses.
With the above in mind, our goal is to develop a single construction for a given cryptographic concept that simultaneously captures any reasonable security property and can be composed to work in any reasonable larger protocol. As such, only a single instance of the scheme needs to be developed and then deployed in a variety of use cases, even those that have not yet been discovered.
Ideal Hash Functions: The Random Oracle Model. Our inspiration will be the random oracle model (ROM) [4], a common heuristic used in cryptography. Here, a hash function is assumed to be so well designed that the only reasonable attacks simply evaluate the hash function as a black box and gain nothing by trying to exploit the particular design. To capture this, the hash function is modeled as a truly random function, accessible by making queries to the function.
A random oracle truly is the “ideal” hash function: it is trivially one-way and collision resistant, the standard security notions for hash functions. But it is also much stronger: it is correlation intractable [7], a good extractor even for computational sources, and much more. When used in a larger system, random oracles can yield provably secure schemes even when standard security properties for hash functions are insufficient. In fact, the most efficient schemes in practice are often only known to be secure using random oracles. As such, the ROM is ubiquitous in cryptography.
Other idealized models have been studied before. Examples include the ideal cipher model [25], the generic group model [26], and more recently ideal symmetric key encryption [2]. However, no prior work considers idealized models for public key cryptosystems.
Ideal Public Key Cryptosystems. In this work, we define and construct the first ideal public key cryptosystems such as public key encryption and digital signatures. By being ideal, our schemes will immediately satisfy a wide class of security properties, including most studied in the literature. Our schemes will be proven to be ideal in the random oracle model using Maurer’s indifferentiability framework [20], under general computational assumptions. We also show that certain classic relations among cryptographic objects also hold in the ideal setting, while discussing cases where such relations fail.
Our goal comes with interesting challenges: on one hand, public key schemes tend to require number-theoretic structure in order to attain the necessary functionality. On the other hand, ideal schemes by definition have essentially no structure. Therefore, our results require novel techniques, including bringing indifferentiability into the public key setting.
1.1 What Is an Ideal Public Key Scheme?
Now, we turn to our results. Our first result is to define, precisely, what an “ideal” public key cryptosystem is. For simplicity, in the following discussion, we will consider the case of two-party non-interactive key exchange (NIKE). Such a scheme consists of two algorithms. \(\mathsf {KEYGEN}\) is a key generation algorithm run by each of two users. We will adopt the convention that the input to \(\mathsf {KEYGEN}\) is the user’s secret key \(\mathsf {SK}\), and the output is the corresponding public key \(\mathsf {PK}\). The two users then exchange their public keys. They then run \(\mathsf {SHAREDKEY}\) to extract a common shared key. \(\mathsf {SHAREDKEY}\) will take as input the public key for one user and the secret key for the other, and output a shared key K. The correctness requirement is that both users arrive at the same key:
whenever \({\mathsf {\MakeUppercase {PK}}}_1={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}}_1)\) and \({\mathsf {\MakeUppercase {PK}}}_2={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}}_2)\).
Any NIKE scheme will have the syntax above and the same correctness requirement. On the other hand, any given NIKE scheme may have additional structural properties that make it insecure in certain settings. For example, if multiple shared keys are generated using the same public key \({\mathsf {\MakeUppercase {PK}}}\) for a given user, the resulting shared keys may be correlated in some algebraic way. In order to be secure in the widest variety of settings, an ideal NIKE scheme should therefore not have any such additional structure over the minimum needed to ensure correctness.
In the case of existing idealized models, the idealization is simply a uniformly random choice of procedures subject to the mandatory correctness requirements. For example, a hash function has no correctness requirement except for determinism; as such its idealization is a random oracle. Likewise, a block cipher must be a (keyed) permutation, and the decryption functionality must be its inverse. As such, the ideal cipher is a random keyed permutation and its inverse.
Therefore, the natural way to model an ideal NIKE scheme is to have all algorithms be random functions. Of course, the correctness requirement means that there will be correlations between the algorithms. We take an ideal NIKE scheme to be two oracles \({\mathsf {\MakeUppercase {KEYGEN}}}\), \({\mathsf {\MakeUppercase {SHAREDKEY}}}\) such that:
-
\({\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})\) is a random injection;
-
\({\mathsf {\MakeUppercase {SHAREDKEY}}}({\mathsf {\MakeUppercase {PK}}},{\mathsf {\MakeUppercase {SK}}})\) is a random function, except that \({\mathsf {\MakeUppercase {SHAREDKEY}}}({\mathsf {\MakeUppercase {PK}}}_1, {\mathsf {\MakeUppercase {SK}}}_2)= {\mathsf {\MakeUppercase {SHAREDKEY}}}({\mathsf {\MakeUppercase {PK}}}_2, {\mathsf {\MakeUppercase {SK}}}_1)\) whenever \({\mathsf {\MakeUppercase {PK}}}_1={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}}_1)\) and \({\mathsf {\MakeUppercase {PK}}}_2={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}}_2)\)Footnote 1.
We emphasize that all functions are public and visible to the attacker and the formal definition for ideal NIKE is given in Sect. 3.1.
1.2 Indifferentiability
Of course, just like a random oracle/generic group/ideal cipher, ideal NIKE cannot exist in the real world. This then begs the question: how do we design and rigorously argue that a NIKE scheme is so well designed that it can be treated as an ideal NIKE scheme in applications?
Barbosa and Farshim [2] offer one possible answer. They build a symmetric key encryption scheme from a hash function. Then, they show, roughly, that if the hash function is ideal (that is, a random oracle), then so is their scheme. Our goal in this work will be to do the same for public key schemes: to build an ideal NIKE scheme assuming that a hash function H is a random oracle.
As in [2], formal justification of ideal security requires care. Suppose we have a construction of an ideal NIKE scheme \(({\mathsf {\MakeUppercase {KEYGEN}}},{\mathsf {\MakeUppercase {SHAREDKEY}}})\) in the random oracle model, meaning each of the algorithms makes queries to a random function H. In the case where H is hidden to the adversary, such a construction is almost trivial, and would essentially reduce to building symmetric key encryption from a PRF. However, Maurer, Renner, and Holenstein [20] observed that this is not enough, since H is a public function and the adversary can query H as well.
Clearly, any construction \(({\mathsf {\MakeUppercase {KEYGEN}}},{\mathsf {\MakeUppercase {SHAREDKEY}}})\) will now be distinguishable from the idealized algorithms, since the adversary can evaluate the algorithms for himself by making queries to H, and checking if the results are consistent with the oracles provided. Instead, what is needed is the stronger notion of indifferentiability, which says that when \(({\mathsf {\MakeUppercase {KEYGEN}}},{\mathsf {\MakeUppercase {SHAREDKEY}}})\) are ideal, it is possible to simulate H by a simulator S which can make queries to \(({\mathsf {\MakeUppercase {KEYGEN}}},{\mathsf {\MakeUppercase {SHAREDKEY}}})\). In the real world, \(({\mathsf {\MakeUppercase {KEYGEN}}},{\mathsf {\MakeUppercase {SHAREDKEY}}})\) are constructed from H per the specification. In the ideal world, \(({\mathsf {\MakeUppercase {KEYGEN}}},{\mathsf {\MakeUppercase {SHAREDKEY}}})\) are the idealized objects, and H is simulated by making queries to the ideal objects. Indifferentiability requires that the two worlds are indistinguishable to an adversary that gets access to all the oracles.
Maurer, Renner, and Holenstein shows that indifferentiability has many desirable properties: it composes well and will be as good as the ideal object in many settings (see Sect. 1.3 below for some limitations).
Therefore, our goal will be to build NIKE which is indifferentiable from ideal NIKE in the random oracle model. As indifferentiability has mostly been used in the symmetric key setting, this will require new techniques to bring indifferentiability into the public key world. Indeed, most works on indifferentiability build ideal objects with minimal correctness requirements: none in the case of random oracles, and bijectivity/injectivity in the case of ideal ciphers/symmetric key encryption. The case of public key cryptosystems requires significantly more structure for correctness. In fact, we face an immediate theoretical barrier: Impagliazzo and Rudich [17] demonstrate that a random oracle is incapable of constructing something as structured as public key encryption, even ignoring the strong indifferentiability requirement.
Instead, we will obtain our needed structure using public key tools. However, public key tools come with too much structure: every term has an algebraic meaning which is not present in the idealized setting. Therefore, our goal will actually be to employ a novel combination of public key techniques together with random oracles in order to eliminate this extra structure. The result will be an indifferentiable NIKE scheme.
1.3 Discussion
Limitations. Before giving our constructions in detail, we briefly discuss limitations. Most importantly, idealized cryptosystems do not exist in the real world. Even more, Canetti, Goldreich, and Halevi [7] demonstrate that no concrete instantiation in the standard model is “as good as” an ideal object. Therefore, idealizations of cryptographic primitives are only heuristic evidence for security.
Nevertheless, the counter-examples are usually somewhat contrived, and do not apply in typical real-world settings. Indeed, in the case of hash functions, significant resources have been invested in analyzing their security, and the best attacks typically treat the hash function as a random oracleFootnote 2. As such, the random oracle appears to be a reasonable approximation to the real world in most settings. By building schemes from such strong hash functions and proving security using indifferentiability, such schemes are essentially “as good as” the ideal schemes, assuming the underlying hash function is ideal.
In fact, the random oracle model is widely used for the construction of new cryptosystems, as it allows security to be justified where no obvious concrete security property for hash functions would suffice. In these cases, the system is typically proven to satisfy the single security property considered. In our case, we are able to rely on the same heuristic treatment of hash functions, and attain ideal security.
Now, Ristenpart, Shacham, and Shrimpton [22] demonstrate the limitations of the indifferentiability framework. In particular, they show that indifferentiability is insufficient for proving security properties defined by multi-stage games. While this potentially precludes certain applications, indifferentiability is still sufficient to prove many security properties such as CCA-security, key-dependent-message and circular security in restricted settings (see [2] for discussion), bounded leakage resilience, and more. We also note that if all but one of the stages are independent of the ideal primitives, then indifferentiability is sufficient. This captures, for example, the usual modeling of deterministic public key encryption in the random oracle model [3]. Even more, in the case where multiple stages depend on the ideal primitives, Mittelbach [21] shows that indifferentiability is sufficient in some settings.
We leave as an interesting direction for future work building ideal public key schemes that can be proven secure in stronger models of indifferentiability such as reset indifferentiability [22] or context-restricted indifferentiability [19].
1.4 Constructing Ideal NIKE
We now turn to our constructions. Our goal will be to combine a standard model NIKE \((\mathsf {keygen},\mathsf {sharedkey})\)—one with concrete mild security properties that are easy to instantiate—with random oracles to obtain an ideal model NIKE \(({\mathsf {\MakeUppercase {KEYGEN}}},{\mathsf {\MakeUppercase {SHAREDKEY}}})\).
Making \({\mathsf {\MakeUppercase {KEYGEN}}}\) indifferentiable. First, we will focus just on \({\mathsf {\MakeUppercase {KEYGEN}}}\), which on its own must be indifferentiable from a random injection. Of course, we could just set \({\mathsf {\MakeUppercase {KEYGEN}}}\) to be a random oracleFootnote 3, but we want to somehow incorporate \(\mathsf {keygen}\) so that it can provide the structure needed when we turn to construct \(\mathsf {SHAREDKEY}\). Nevertheless, a random oracle (or some other idealized object) is needed somewhere in the construction. As a first attempt, we could consider defining \({\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})=H(\mathsf {keygen}({\mathsf {\MakeUppercase {SK}}}))\), hashing the output of \(\mathsf {keygen}\) to eliminate any structure on the public keys. This, unfortunately, does not work. For example, \(\mathsf {keygen}\) may not be collision resistant, and any collision for \(\mathsf {keygen}\) will therefore give a collision for \({\mathsf {\MakeUppercase {KEYGEN}}}\). The resulting \({\mathsf {\MakeUppercase {KEYGEN}}}\) would then clearly be distinguishable from a random function without even making queries to H.
Attack 1. Even if we assume \(\mathsf {keygen}\) was collision resistant, the scheme would still not be indifferentiable. Indeed, the attacker can query \({\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})\), evaluate \(\mathsf {pk}=\mathsf {keygen}({\mathsf {\MakeUppercase {SK}}})\) for itself, and then query H on \(\mathsf {pk}\). The simulator now has to simulate H, and for indifferentiability to hold it must know how to set \(H(\mathsf {pk})={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})\). However, the simulator only gets to see \(\mathsf {pk}\) and somehow must query \({\mathsf {\MakeUppercase {KEYGEN}}}\) on \({\mathsf {\MakeUppercase {SK}}}\). Extracting \({\mathsf {\MakeUppercase {SK}}}\) from \(\mathsf {pk}\) involves breaking the original NIKE, which is presumably intractable.
A different approach would be to define \({\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})=\mathsf {keygen}(H({\mathsf {\MakeUppercase {SK}}}))\). The problem here is that \(\mathsf {keygen}\) may output very structured public keys, which are clearly distinguishable from random. One possibility is to assume \(\mathsf {keygen}\) has pseudorandom public keys; that is, that \(\mathsf {keygen}\) applied to uniformly random coins gives a pseudorandom output.
Attack 2. However, we still have a problem. Indeed, suppose the adversary queries \({\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})\), which in the ideal world will give a random string. Then the adversary queries \(H({\mathsf {\MakeUppercase {SK}}})\). In the ideal world, the simulator must set \(H({\mathsf {\MakeUppercase {SK}}})=r\) such that \(\mathsf {keygen}(r)={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})\). This may be flat out impossible (in the case where the range of \(\mathsf {keygen}\) is sparse), and at a minimum requires inverting \(\mathsf {keygen}\), again breaking the security of the NIKE scheme.
A third approach which does work is to combine the two: \({\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})=H_1(\mathsf {keygen}(H_0({\mathsf {\MakeUppercase {SK}}})))\). Now both \(H_0, H_1\) are random oracles that are simulated by the simulator. This actually gives indifferentiability: when the adversary queries \(H_0({\mathsf {\MakeUppercase {SK}}})\), the simulator will program \(H_0({\mathsf {\MakeUppercase {SK}}})=r\) for a randomly chosen r. Then it will program \(H_1(\mathsf {keygen}(r))={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})\) by querying \({\mathsf {\MakeUppercase {KEYGEN}}}\). The only way a problem can arise is if the input \(\mathsf {keygen}(r)\) was already programmed in \(H_1\). All that we need to exclude such a possibility is that \(\mathsf {keygen}\) is well-spread: that the distribution of outputs given a uniformly random input has high min-entropy. This follows easily from the security of the NIKE protocol.
The takeaway from the above discussion is that inputs and outputs for a standard-model scheme must be processed by idealized objects; this is the only way that the simulator can obtain enough information to be indifferentiable.
Making \({\mathsf {\MakeUppercase {SHAREDKEY}}}\) Indifferentiable. Next, we move to define \({\mathsf {\MakeUppercase {SHAREDKEY}}}\) in a way to make the joint oracles \(({\mathsf {\MakeUppercase {KEYGEN}}},{\mathsf {\MakeUppercase {SHAREDKEY}}})\) indifferentiable from an ideal NIKE protocol.
Unfortunately, we immediately run into problems. We somehow need to design the shared-key algorithm \({\mathsf {\MakeUppercase {SHAREDKEY}}}\) to take as input one public key \({\mathsf {\MakeUppercase {PK}}}_1=H_1(\mathsf {keygen}(H_0({\mathsf {\MakeUppercase {SK}}}_1)))\), as well as another secret key \({\mathsf {\MakeUppercase {SK}}}_2\). It will output a shared key K. Importantly, we need to maintain the correctness requirement that \({\mathsf {\MakeUppercase {SHAREDKEY}}}( {\mathsf {\MakeUppercase {PK}}}_1,{\mathsf {\MakeUppercase {SK}}}_2)={\mathsf {\MakeUppercase {SHAREDKEY}}}({\mathsf {\MakeUppercase {PK}}}_2,{\mathsf {\MakeUppercase {SK}}}_1)\) whenever \({\mathsf {\MakeUppercase {PK}}}_1={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}}_1)\) and \({\mathsf {\MakeUppercase {PK}}}_2={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}}_2)\).
Guided by Impagliazzo and Rudich’s [17] barrier, we cannot rely on the functionalities of the random oracles \(H_0, H_1\) for this. Instead, we must use the functionality provided by \((\mathsf {keygen}, \mathsf {sharedkey})\). However, \(\mathsf {sharedkey}\) expects output from \(\mathsf {keygen}\), and this value has been completely scrambled by the hash function \(H_1\), which is un-invertible. Therefore, \({\mathsf {\MakeUppercase {SHAREDKEY}}}\) has no way to apply \(\mathsf {sharedkey}\) in a meaningful way.
So we need some way to preserve the structure of the output \(\mathsf {keygen}\) while still allowing for an indifferentiability proof. But at the same time, we cannot just expose the output of \(\mathsf {keygen}\) in the clear, as explained above.
Our solution is to replace \(H_1\) with a random permutation P such that both P and \(P^{-1}\) are publicly accessible (we discuss instantiating the random permutation below). We then have that
Then we can define \({\mathsf {\MakeUppercase {SHAREDKEY}}}({\mathsf {\MakeUppercase {PK}}},{\mathsf {\MakeUppercase {SK}}})=\mathsf {sharedkey}(P({\mathsf {\MakeUppercase {PK}}}),H_0({\mathsf {\MakeUppercase {SK}}}))\). Note that, defining \({\mathsf {\MakeUppercase {SHAREDKEY}}}\) in this way achieves the desired correctness guarantee, which follows simply from the correctness of \((\mathsf {keygen, sharedkey})\).
Attack 3. However, by allowing the permutation P to be invertible, we have invalidated our indifferentiability proof above for \({\mathsf {\MakeUppercase {KEYGEN}}}\). Suppose for example that \(\mathsf {keygen}\)’s outputs are easily distinguishable from random. Then an attacker can compute \({\mathsf {\MakeUppercase {PK}}}={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})\), and then query P on either \({\mathsf {\MakeUppercase {PK}}}\) or a random string r. In the case of a random string, P(r) will itself be essentially a random string. On the other hand, \(P({\mathsf {\MakeUppercase {PK}}})\) will be an output of \(\mathsf {keygen}\), and hence distinguishable from random. The problem is that the simulator defining P only gets to see r and has no way to know whether r came from \({\mathsf {\MakeUppercase {KEYGEN}}}\) or was just a random string. Therefore, the attacker can fool the simulator, leading to a distinguishing attack.
To avoid this problem, we will assume the standard-model NIKE protocol has pseudorandom public keys. In this case, the simulator will always respond to a P using a fresh random output of \(\mathsf {keygen}\). In the case where the query to P was on a random r, the result will look random to the adversary. On the other hand, if the query was on a \({\mathsf {\MakeUppercase {PK}}}={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})\), the simulator is ready to program any subsequent \(H_0({\mathsf {\MakeUppercase {SK}}})\) query to satisfy \(P({\mathsf {\MakeUppercase {PK}}})=\mathsf {keygen}(H_0({\mathsf {\MakeUppercase {SK}}}))\).
Attack 4. Many more problems still arise, similar to the problems above faced when trying to define \({\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}})=\mathsf {keygen}(H({\mathsf {\MakeUppercase {SK}}}))\). Namely, the adversary could first call the query \(k={\mathsf {\MakeUppercase {SHAREDKEY}}}({\mathsf {\MakeUppercase {PK}}}',{\mathsf {\MakeUppercase {SK}}})\), which in the ideal world will give a random string. Then the adversary makes queries to \(P, H_0\) and computes \(\mathsf {sharedkey}(P({\mathsf {\MakeUppercase {PK}}}'),H_0({\mathsf {\MakeUppercase {SK}}}))\) for itself. In the ideal world, the simulator must set \(P({\mathsf {\MakeUppercase {PK}}}')=r\) and \(H_0({\mathsf {\MakeUppercase {SK}}})=s\) such that \(\mathsf {sharedkey}(r,s)=k\). But this involves inverting \(\mathsf {sharedkey}\) on k, which may be computationally infeasible. Worse yet, the adversary could do this for \({\mathsf {\MakeUppercase {PK}}}_1',\dots ,{\mathsf {\MakeUppercase {PK}}}_\ell '\) and \({\mathsf {\MakeUppercase {SK}}}_1,\dots ,{\mathsf {\MakeUppercase {SK}}}_\ell \), obtaining \(\ell ^2\) different random and independent \(k_{i,j}\) values from \({\mathsf {\MakeUppercase {SHAREDKEY}}}\) by considering all possible \({\mathsf {\MakeUppercase {PK}}}_i',{\mathsf {\MakeUppercase {SK}}}_j\) pairs. The simulator then needs to somehow find \(r_1,\dots ,r_\ell ,s_1,\dots ,s_\ell \) such that \(\mathsf {sharedkey}(r_i,s_j)=k_{i,j}\), where \(k_{i,j}\) are each random independent strings. This is clearly impossible for large enough \(\ell \), since it would allow for compressing an \(O(\ell ^2)\)-bit random string into \(O(\ell )\) bits.
Our solution is to apply one more hash function, this time to the output of \(\mathsf {sharedkey}\): \({\mathsf {\MakeUppercase {SHAREDKEY}}}({\mathsf {\MakeUppercase {PK}}}_1,{\mathsf {\MakeUppercase {SK}}}_2)=H_1(\mathsf {sharedkey}(P({\mathsf {\MakeUppercase {PK}}}_1),H_0({\mathsf {\MakeUppercase {SK}}}_2)))\). Now, all we need is that \(\mathsf {sharedkey}(r_i,s_j)\) are all distinct for different i, j pairs, which follows with high probability from the security of the NIKE scheme. Then we can simply program \(H_1(\mathsf {sharedkey}(r_i,s_j))=k_{i,j}\).
Attack 5. This construction unfortunately is still insecure: the adversary first samples \(\mathsf {sk_1}\) and \(\mathsf {SK_2}\), then it queries \(\mathsf {PK_2} = \mathsf {KEYGEN}(\mathsf {SK_2}), \mathsf {pk_2} = P(\mathsf {PK_2})\), then calculates \(k = \mathsf {sharedkey}(\mathsf {pk_2, sk_1})\) and queries \(H_1(k)\). After that, the adversary calculates \(\mathsf {pk_1} = \mathsf {keygen}(\mathsf {sk_1})\), and queries \(\mathsf {PK_1} = P^{-1}(\mathsf { pk_1})\). Next it calls \(k'= \mathsf {SHAREDKEY}(\mathsf {PK_1, SK_2} )\) and finally tests \(k' \overset{?}{=} H_1(k)\). In the real world, the test always passes, while to achieve indifferentiability, the simulator has to output a proper \(H_1(k)\). Unfortunately, until the query \(H_1(k)\), simulator knows nothing of \((\mathsf {sk_1, SK_2})\) (it only has \(\mathsf {KEYGEN(SK_2)}\)), which means that it cannot program \(H_1(k)\) to be \(k'\). Therefore test fails with overwhelming probability in the ideal world. To get prevent this attack, we present our final construction:
where \({\mathsf {\MakeUppercase {PK}}}_2={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}}_2)=P^{-1}(\mathsf {keygen}(H_0({\mathsf {\MakeUppercase {SK}}}_2)))\)Footnote 4. How does this help? We note that, in the final construction, by including \({\mathsf {\MakeUppercase {PK}}}_1,{\mathsf {\MakeUppercase {PK}}}_2\) in the \(H_1\) queries, we force the adversary to query \(\mathsf {PK_1} = P^{-1}(\mathsf {pk_1})\) before the \(H_1\) query. This allows the simulator to program \(P^{-1}\) in a way that allows it to correctly answer the later \(H_1\) query. In particular, it samples \(\mathsf { SK_1}\) itself and responds to the \(P^{-1}\) query with \(\mathsf {PK_1}= \mathsf {KEYGEN}(\mathsf {SK_1})\). Afterward, when then adversary makes the query \(H_1(\{{\mathsf {\MakeUppercase {PK}}}_1, {\mathsf {\MakeUppercase {PK}}}_2\}, k)\), the simulator will respond with \(\mathsf {SHAREDKEY}(\mathsf {PK_2, SK_1})\), which is always identical to \(\mathsf {SHAREDKEY}(\mathsf {PK_1, SK_2})\).
Attack 6. Even with our final construction, we must be careful. Suppose that it was possible for the adversary to choose a public key \(\mathsf {pk}^*\) such that it can guess the value of \(\mathsf {sharedkey}(\mathsf {pk}^*,\mathsf {sk})\) for a random (hidden) \(\mathsf {sk}\), then there is still an attack. Namely, the adversary queries \({\mathsf {\MakeUppercase {PK}}}^*=P^{-1}(\mathsf {pk}^*)\) and \({\mathsf {\MakeUppercase {PK}}}=\mathsf {KEYGEN}({\mathsf {\MakeUppercase {SK}}})\) for a random \({\mathsf {\MakeUppercase {SK}}}\). It then guesses the value \(t^*_0\) of \(\mathsf {sharedkey}(\mathsf {pk}^*,H_0({\mathsf {\MakeUppercase {SK}}}))\), without ever actually querying \(H_0\), then it randomly samples an additional string \(t^*_1\) such that the simulator fails to distinguish \(t^*_0\) from \(t^*_1\) with high probability. Finally, it flips a coin b, and queries \(k=H_1(\{{\mathsf {\MakeUppercase {PK}}}^*,{\mathsf {\MakeUppercase {PK}}}\},t^*_b)\); if \(b = 0\) it checks that the result is equal to \({\mathsf {\MakeUppercase {SHAREDKEY}}}({\mathsf {\MakeUppercase {PK}}}^*,{\mathsf {\MakeUppercase {SK}}})\) and else it checks that the result is not equal to \({\mathsf {\MakeUppercase {SHAREDKEY}}}({\mathsf {\MakeUppercase {PK}}}^*,{\mathsf {\MakeUppercase {SK}}})\). In the real world, if \(b = 0\), this check will pass as long as the guess \(t^*_0\) is correct, and if \(b=1\), it will pass as long as no collision occurs. On the other hand, in the ideal world, although the simulator can simulate \(k=H_1(\{{\mathsf {\MakeUppercase {PK}}}^*,{\mathsf {\MakeUppercase {PK}}}\},t^*_0)\) correctly without knowing \({\mathsf {\MakeUppercase {SK}}}\) (the technique in Attack 5), it doesn’t know the query corresponds to \(t^*_0\) or \(t^*_1\). As a result, the check would fail with a noticeable probability. Our solution is to add another security requirement for the NIKE scheme, which we call entropic shared keys, insisting that for any \(\mathsf {pk}^*\) of the adversary’s choosing, the adversary cannot guess \(\mathsf {sharedkey}(\mathsf {pk}^*,\mathsf {sk})\) except for negligible probability.
Attack 7. One last attack strategy: the attacker could first query \({\mathsf {\MakeUppercase {PK}}}_1={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}}_1), {\mathsf {\MakeUppercase {PK}}}_2={\mathsf {\MakeUppercase {KEYGEN}}}({\mathsf {\MakeUppercase {SK}}}_2),k={\mathsf {\MakeUppercase {SHAREDKEY}}}({\mathsf {\MakeUppercase {PK}}}_1,{\mathsf {\MakeUppercase {SK}}}_2)\). Then, it could query \(r_1=P({\mathsf {\MakeUppercase {PK}}}_1),r_2=P({\mathsf {\MakeUppercase {PK}}}_2)\). Finally, it could treat \(r_1,r_2\) as the messages in the standard-model NIKE protocol, and guess the shared key t for the protocol. Then it could query \(H_1\) on t (and \(\{{\mathsf {\MakeUppercase {PK}}}_1,{\mathsf {\MakeUppercase {PK}}}_2\}\)). In the real world, the result \(H_1(\{{\mathsf {\MakeUppercase {PK}}}_1,{\mathsf {\MakeUppercase {PK}}}_2\},t)\) would be equal to k, so the simulator in the ideal world needs to be able to set \(H_1(\{{\mathsf {\MakeUppercase {PK}}}_1,{\mathsf {\MakeUppercase {PK}}}_2\},t)=k\). At this point, the simulator has \({\mathsf {\MakeUppercase {PK}}}_1,{\mathsf {\MakeUppercase {PK}}}_2,t\). But the simulator has no knowledge of \({\mathsf {\MakeUppercase {SK}}}_1\) or \({\mathsf {\MakeUppercase {SK}}}_2\). Therefore it has no way of guessing the correct input to \({\mathsf {\MakeUppercase {SHAREDKEY}}}\) to obtain k, as doing so requires recovering either \({\mathsf {\MakeUppercase {SK}}}_1\) or \({\mathsf {\MakeUppercase {SK}}}_2\) by inverting \({\mathsf {\MakeUppercase {KEYGEN}}}\).
Of course, this attack requires the adversary to guess the shared key t from the public messages \(r_1,r_2\) in the standard-model NIKE scheme, which should be impossible. One difficulty is that, in our construction, the adversary implicitly has access to a kind of verification oracle for the standard-model NIKE, which allows it to input \(r_1,r_2\) as well as a guess \(k'\) for k, and learn if the guess was correct. One of the \(r_1,r_2\) can even be chosen by the adversary. To see how such an oracle arises, imagine the adversary queried \({\mathsf {\MakeUppercase {KEYGEN}}}( sk _1)\) to get \({\mathsf {\MakeUppercase {PK}}}_1\) and \(P({\mathsf {\MakeUppercase {PK}}}_1)\) to get \(r_1\). Then for an \(r_2\) of its choice, it queries \(P^{-1}(r_2)\) to get \({\mathsf {\MakeUppercase {PK}}}_2\). Next, it queries \({\mathsf {\MakeUppercase {SHAREDKEY}}}({\mathsf {\MakeUppercase {PK}}}_2,{\mathsf {\MakeUppercase {SK}}}_1)\) to get K, and \(H_1({\mathsf {\MakeUppercase {PK}}}_2,{\mathsf {\MakeUppercase {PK}}}_1,k')\) to get \(K'\). The correctness of our algorithms implies that \(K'=K\) if and only if \(k'=k\).
Thus, if our NIKE scheme is only secure against passive attacks, it might be vulnerable to this attack vector. Concretely, if the underlying standard-model NIKE is the isogeny-based scheme of [18], then the active attack of [16] can be mounted against our scheme. Instead, we will require a stronger notion of NIKE security for the standard-model scheme, which we call semi-active unpredictable shared keys. Here, we require that the shared key is unpredictable, even if the adversary is given the verification oracles as described above. Such NIKE can easily be constructed under standard assumptions.
While we have protected against certain natural attacks, we need to argue indifferentiability against all possible attacks. To do so we use a careful simulation strategy for \(H_0, H_1, P, P^{-1}\), and prove indifferentiability through a careful sequence of hybrids. In essence, each step in the hybrid argument corresponds roughly to one of the attack strategies discussed above, and our proof shows that these attacks do not work, demonstrating the indistinguishability of the hybrids.
Constructing \(P, P^{-1}\). Our random permutation \(P, P^{-1}\) can easily be instantiated using the ideal cipher model in the setting where the key space contains only a single element. We note that indifferentiable ideal ciphers can be constructed from random oracles [10].
Therefore, all we need for our construction is three random oracles. Multiple random oracles can easily be built from a single random oracle by prefixing the oracle index to the input. Finally, an indifferentiable random oracle of any domain/range can be constructed from a fixed-size random oracle [8].
The Role of P in the Proof. It is natural to wonder what role P plays in the actual security of our scheme. After all, since \(P^{-1}\) is publicly invertible using P, the adversary can easily undo the application of \(P^{-1}\) to the output of \({\mathsf {\MakeUppercase {KEYGEN}}}\). So it may seem that P is a superfluous artifact of the proof.
There are multiple ways to address this question. One answer is that without P, there would be no way to have a computationally efficient simulator as discussed above. One could consider an inefficient simulator, but this would correspond to a weaker notion of indifferentiability. This notion of indifferentiability would be useless when composing with protocols that have computational rather than statistical security. What’s more, we would actually be unable to prove even this weaker form. Indeed, our proof crucially relies on the computational security of the standard-model NIKE protocol. Since the inefficient simulator would essentially have to break the security of the NIKE protocol, it would be impossible to carry out the proof.
A higher-level answer is that by including P—which is under full control of the simulator—the simulator gets to learn extra information about what values the adversary is interested in. In particular, in order to relate the ideal oracles to the standard-model scheme, the adversary must always send a query to the simulator. This extra information provided by making such queries is exactly what the simulator needs for the proof to go through. This is a common phenomenon in random-oracle proofs, where hashing sometimes has no obvious role except to provide a reduction/simulator with necessary information.
Yet another answer is that, if P is omitted, the scheme is actually insecure in some settings. For example, an ideal NIKE satisfies the property that an adversary, given Alice’s secret key and half of Bob’s public key, cannot compute the shared key between Alice and Bob. Now, consider the case where the standard model NIKE does not satisfy this requirement. Then if we do not include P, our construction does not satisfy the requirement either. Instead, by including P, an adversary who gets half of Bob’s ideal public key cannot invert the permutation to recover any information about the corresponding standard-model public key. It then follows that the adversary cannot guess the shared key.
1.5 Extending to Other Idealized Cryptosystems
We now turn our attention to extending the above results to other cryptosystems. First, we use our ideal NIKE scheme to construct ideal public key encryption (PKE). Note that ideal public key encryption is in particular CCA secure, whereas the standard way to turn a NIKE scheme into a PKE scheme is never CCA secure. In order to make the scheme CCA secure, a natural starting point is the Fujisaki-Okamoto (FO) transform [15]. While this transformation applied to our ideal NIKE certainly achieves CCA security, it unfortunately is not indifferentiable when applied to our NIKE. The reasons are several-fold, and should come as no surprise given that FO was never designed to achieve indifferentiability.
For starters, recall from our NIKE discussion that all inputs and outputs of the algorithms need to be passed through ideal objects under the simulator’s control. In the FO transformation, this is not the case. Another reason why FO does not give indifferentiability is that the FO transform allows for encryption randomness to be recovered during decryption; in fact, this is a crucial feature of the CCA security proof. On the other hand, such encryption schemes cannot be ideal, since ideal encryption schemes guarantee that the encryption randomness is hidden even to the decrypterFootnote 5.
To overcome these issues, we first show a careful transformation from our ideal NIKE into ideal deterministic public key encryption (DPKE). By focusing first on DPKE, we side-step the randomness issue. Our transformation is inspired by the FO transform, but in order to ensure that all inputs/outputs are passed through oracles under the simulator’s control, we employ our random permutation trick again.
Finally, we turn to convert ideal DPKE into ideal PKE. The usual conversion (simply including the encryption randomness as part of the message) does not suffice, again because the usual conversion allows the decrypter to recover the encryption randomness. We instead essentially hide the randomness by hashing with a random oracle. This, however, requires care in order to enable a complete indifferentiability proof.
Ideal Signatures. Finally, we investigate constructing ideal signatures. While in the standard model signatures can in principle be built from one-way functions and therefore random oracles, we observe that the situation for ideal signatures is much more challenging. For example, an ideal signature scheme will be unique, meaning for any message/public key, only a single signature will verify. On the other hand, constructing unique signatures even under standard security notions is difficult, and the only known constructions require strong number-theoretic tools such as bilinear maps.
We instead assume a building block as a standard-model signature scheme with unique signatures, as well as some other mild security properties which can be easily instantiated using bilinear maps. We show that such a scheme can, in fact, be turned into ideal signatures using similar ideas to the above.
1.6 Instantiations
Our NIKE schemes require a standard-model NIKE. Unfortunately, we cannot use a truly arbitrary standard model NIKE, as in addition to the semi-active unpredictable shared keys, we also need pseudorandom public keys and entropic shared keys. As such, we need to make sure such a scheme can be instantiated. Our other results similarly require standard-model schemes where various outputs of the schemes are pseudorandom bit strings.
We note that the entropic shared key requirement is satisfied by all constructions we are aware of and the semi-active unpredictable shared keys can be achieved on cryptographic groups or bilinear maps [14], under doubly-strong CDH assumption. On the other hand, the requirement of pseudorandom public keys is slightly non-trivial. Many number-theoretic constructions have public keys that are elements in \({{\mathbb {Z}}}_q^k\) for some modulus k; even if the public keys are pseudorandom in these sets, there may be no way to represent a random element of \({{\mathbb {Z}}}_q^k\) as a random bit string (which we need in order to apply the ideal permutation P), since \(q^k=|{{\mathbb {Z}}}_q^k|\) may be far from a power of 2.
However, it will usually be easy to map such public keys to random strings in \(\{0,1\}^n\) for some integer n. For example, in the case \(k=1\), suppose we are given a (pseudo)random element \(\mathsf {pk}\in {{\mathbb {Z}}}_q\). Let n be some integer such that \(n\ge \lambda +\log _2 q\) for a security parameter \(\lambda \). Let \(t=\lfloor 2^n/q\rfloor \) be the largest integer such that \(tq\le 2^n\). Then we can extend \(\mathsf {pk}\) into a random element \(\mathsf {pk}'\) in \({{\mathbb {Z}}}_{tq}\) by setting \(\mathsf {pk}'=\mathsf {pk}+a q\), where a is a random integer in \({{\mathbb {Z}}}_t\). Finally, we note that a random integer in \({{\mathbb {Z}}}_{tq}\) is distributed exponentially close (in \(\lambda \)) to a random integer in \({{\mathbb {Z}}}_{2^n}\).
We can similarly handle the case \(k>1\) by bijecting public keys into \({{\mathbb {Z}}}_{q^k}\) in the standard way. Such conversions can be applied to Diffie-Hellman key agreement. The result that we attain our NIKE results under doubly-strong-CDH, whereas our signature scheme requires CDH in bilinear map groups. The full details can be found in [27].
2 Background
Notation. Throughout this paper, \(\lambda \in \mathbb {N}\) denotes the security parameter. We let \(\mathbb {N}\) be the set of non-negative integers, including zero and \(\{0,1\}^*\) denote the set of all finite-length bit strings, including the empty string \(\epsilon \) (\(\{0,1\}^0 = \epsilon \)). For two bit strings, X and Y, X||Y denotes string concatenation and (X, Y) denotes a uniquely decodable encoding of X and Y. The length of a string X is denoted by |X|.
For a finite set \(\mathcal {S}\), we denote \(s \leftarrow \mathcal {S}\) the process of sampling s uniformly from \(\mathcal {S}\). For a probabilistic algorithm A, we denote \(y \leftarrow A(x;R)\) the process of running A on inputs x and randomness R, and assigning y the result. We let \(\mathcal {R}_A\) denote the randomness space of A; we require \(\mathcal {R}_A\) to be the form \(\mathcal {R}_A = \{0,1\}^r\). We write \(y \leftarrow A(x)\) for \(y \leftarrow A(x, R)\) with uniformly chosen \(R \in \mathcal {R}_A\), and we write \(y_1, \ldots , y_m \leftarrow A(x)\) for \(y_1 \leftarrow A(x), \ldots , y_m \leftarrow A(x)\) with fresh randomness in each execution. If A’s running time is polynomial in \(\lambda \), then A is called probabilistic polynomial-time (PPT). We say a function \(\mu (n)\) is negligible if \(\mu \in o(n^{-\omega (1)})\), and is non-negligible otherwise. We let \(\mathsf {negl}(n)\) denote an arbitrary negligible function. If we say some p(n) is \(\mathsf {poly}\), we mean that there is some polynomial q such that for all sufficiently large n, \(p(n) \le q(n)\). We say a function \(\rho (n)\) is noticeable if the inverse \(1/\rho (n)\) is \(\mathsf {poly}\). We use boldface to denote vector, i.e. \({\textit{\textbf{m}}}\); we denote \({\textit{\textbf{m}}}_i\) as the i-th component of \({\textit{\textbf{m}}}\) and \(|{\textit{\textbf{m}}}|\) as the length of \({\textit{\textbf{m}}}\).
Random Oracle Model (ROM). Random oracle model is an idealized model proposed by Bellare and Rogaway [4]. ROM formalizes a model (a theoretical black box) which responds to any unique query with a truly random string, and if the query is repeated, the response would be consistent. More concretely, a random oracle model has a publicly accessible hash function \(H: \{0,1\}^* \rightarrow \{0,1\}^n\) such that:
-
1.
for any x, every bit of H(x) is truly random;
-
2.
for any \(x \ne y\), H(x) and H(y) are independent.
Ideal Cipher Model (ICM). The ideal cipher model is another idealized model which is firstly proposed by Shannon [25] and then formalized by Black [5]. This model also responds to any unique query with a truly random string. While, instead of having a publicly accessible random function, ideal cipher model has a publicly accessible ideal cipher \(E : \{0,1\}^k \times \{0,1\}^n \rightarrow \{0, 1\}^{n}\). Specifically, E is an ideal cipher along with a k-bit key and n-bit input/output such that:
-
1.
for any pair (k, x), every bit of E(k, x) is truly random;
-
2.
for any fix key k, \(E(k, *)\) is a random permutation;
-
3.
for any \(k_1 \ne k_2\) and (x, y), \(E(k_1, x)\) and \(E(k_2, y)\) are independent.
Moreover, any adversary interacting with an ideal cipher model would be given access to both the cipher and its inverse. The following definitions in this part highly rely on [2] and we roughly use its text here.
Games. An n-adversary game \(\mathcal {G}\) is a Turing machine, denoted as \(\mathcal {G}^{\varSigma , \mathcal {A}_1, \ldots , \mathcal {A}_n}\), where \(\varSigma \) is a system and \(\mathcal {A}_i\) are adversarial algorithms that can keep full local state but might only communicate with each other through \(\mathcal {G}\). If we say a n-adversary game \(\mathcal {G}_n \) is reducible to an m-adversary game \(\mathcal {G}_m \), we mean that, for any \((\mathcal {A}_1, \ldots , \mathcal {A}_n)\), there are \((\mathcal {A}_1', \ldots , \mathcal {A}_m')\) such that for any system \(\varSigma \) we have that \(\mathcal {G}_n^{\varSigma , \mathcal {A}_1, \ldots , \mathcal {A}_n} = \mathcal {G}_m^{\varSigma , \mathcal {A}_1', \ldots , \mathcal {A}_m' }\). A game \(\mathcal {G}\) is called a n-stage game [22] if \(\mathcal {G}\) is an n-adversary game and it cannot be reducible to any m-adversary game, where \(m <n \). In particular, for any single-stage game \(\mathcal {G}_{\varSigma , \mathcal {A}}\), we can trivially rewrite it as \(\overline{\mathcal {A}}^{\overline{\mathcal {G}}^{\varSigma } }\), where \(\overline{\mathcal {G}}\) is an oracle machine and \(\overline{\mathcal {A}}\) is an adversarial algorithm, and \(\overline{\mathcal {A}}\) is compatible with this oracle machine \(\overline{\mathcal {G}}\). Moreover, we say two games are equivalent if they are reducible in both directions.
Random Functions. Let \(\mathcal X\) and \(\mathcal Y\) be two finite sets, we denote \(\mathcal {F}[\mathcal {X} \rightarrow \mathcal {Y}]\) to be the set of all functions that map from \(\mathcal X\) to \(\mathcal Y\). If we say a function \(F: \mathcal {X}\rightarrow \mathcal {Y}\) is a random function, we mean that F is uniformly sampled from \(\mathcal {F}[\mathcal {X} \rightarrow \mathcal {Y}]\). Moreover, if F grants oracle accesses to all parties (honest and adversarial) in a black-box manner, then we treat F as an idealized model.
Random Injections. Similarly, let \(\mathcal{X}\) and \(\mathcal{Y}\) be two sets such that \(|\mathcal{X}| \le |\mathcal{Y}|\), we define \(\mathcal {I}[\mathcal{X}\rightarrow \mathcal{Y}]\) to be the set of all injections that map from \(\mathcal{X}\) to \(\mathcal{Y}\). If we say a function \(F: \mathcal {X}\rightarrow \mathcal {Y}\) is a random injection, we mean that F is uniformly sampled from \(\mathcal {I}[\mathcal {X} \rightarrow \mathcal {Y}]\).
Lazy Samplers. Lazy samplers are algorithmic procedures, to simulate various ideal objects along with arbitrary domain and range, by lazily sampling function at each point. Those ideal objects include: random oracle model, ideal cipher model, random functions and random injections [24].
2.1 Public Key Primitives
In this part, we recall the definitions of the public key primitives that we consider in our work.
Non-Interactive Key Exchange (NIKE) [11]. NIKE is a cryptographic primitive which enables two parties, who know the public keys of each other, to agree on a symmetric shared key without requiring any interaction. It consists of two algorithms: \( \mathsf {NIKE{.}keygen}\) and \(\mathsf {NIKE{.}sharedkey}\) together with a shared key space \(\mathcal {SHK}\).
-
\( \mathsf {NIKE{.}keygen{:}}\) Given input a secret key \(\mathsf {sk}\), the algorithm outputs a public key \(\mathsf { pk}\);
-
\(\mathsf {NIKE{.}sharedkey}\) Given inputs a public key \(\mathsf { pk_1}\) and a secret key \(\mathsf { sk_2}\), the algorithm outputs a shared key \(\mathsf {shk} \in \mathcal {SHK} \).
For correctness, we require that, for any two key pairs \((\mathsf {pk_1, sk_1}), (\mathsf {pk_2, sk_2})\), the system satisfies:

Public Key Encryption (PKE) [11]. A public-key encryption scheme consists of three algorithms: \(\mathsf { PKE{.}keygen, PKE{.}enc, PKE{.}dec}\) together with a message space \(\mathcal{M}\). Formally,
-
\(\mathsf {PKE{.}keygen}\) Given input a secret key \(\mathsf {sk}\), the algorithm outputs a public key \(\mathsf {pk}\);
-
\(\mathsf {PKE{.}enc}\) Given inputs a public key \(\mathsf { pk}\) and \(m \in \mathcal{M}\), the algorithm outputs a ciphertext \(\mathsf {c} = \mathsf {PKE{.}enc}(\mathsf {pk}, \mathsf {m}) \);
-
\(\mathsf {PKE{.}dec}\) Given inputs a secret key \(\mathsf { sk}\) and a ciphertext \(\mathsf { c}\), the algorithm outputs either a plaintext \(\mathsf { m}\) or \(\perp \).
For correctness, we require that, for any key pair \((\mathsf {pk, sk})(\mathsf {pk} = \mathsf {PKE{.}keygen(sk)})\) and \(\mathsf { m} \in \mathcal M\), the scheme satisfies:

Digital Signature [23]. A digital signature scheme consists of three algorithms: \(\mathsf {Sig{.}keygen, Sig{.}sign, Sig{.}ver}\) along with a message space \(\mathcal {M}\). Formally,
-
\(\mathsf { Sig{.}keygen}\) Given input a sign key \(\mathsf { sk}\), the algorithm outputs a verification key \(\mathsf { vk}\);
-
\(\mathsf { Sig{.}sign}\) Given inputs a sign key \(\mathsf { sk}\) and a message \(\mathsf { m} \in \mathcal{M}\), the algorithm outputs a signature \(\sigma = \mathsf {Sig{.}sign(sk, m)}\);
-
\(\mathsf { Sig{.}ver}\) Given inputs a signature \(\sigma \), a message and a verification key \(\mathsf { vk}\), outputs either 1 or 0.
For correctness, we require that, for any key pair \((\mathsf {sk}, \mathsf {vk}) (\mathsf {vk} = \mathsf {Sig{.}keygen}(\mathsf {sk}))\) and \(\mathsf {m} \leftarrow \mathcal M\), the signature scheme satisfies:

2.2 Indifferentiability
For indifferentiability, significant parts of the discussion in this section is based on [2]. In [20], Maurer, Renner and Holenstein (MRH) propose the indifferentiability framework, which formalizes a set of necessary and sufficient conditions for one system to securely be replaced with another one in a wide class of environments. This framework has been used to prove the structural soundness of a number of cryptographic primitives, which includes hash functions [8, 12], blockciphers [1, 10, 13], domain extenders [9] and authenticated encryption with associated data [2]. In the following, we first recall the definition of indifferentiability.
A random system \(\mathrm{\Sigma := (\Sigma {.}hon, \Sigma {.}adv)}\) is accessible via two interfaces \(\mathrm{\Sigma {.}hon}\) and \(\mathrm{\Sigma {.}adv}\), where \(\mathrm{\Sigma {.}hon}\) provides a honest interface through which the system can be accessed by all parties and \(\mathrm{\Sigma {.}adv}\) models the adversarial access to the inner working part of \(\mathrm \Sigma \). Typically, a system implements either some ideal objects \(\mathcal{F}\), or a construction \(C^{\mathcal{F}'}\), which applies some underlying ideal objects \(\mathcal{F}'\).
Definition 1
(Indifferentiability [2, 20]). Let \(\mathrm \Sigma _1\) and \(\mathrm \Sigma _2\) be two systems and \(\mathcal{S}\) be a simulator. The indifferentiability advantage of a differentiator \(\mathcal D\) against \((\mathrm \Sigma _1, \Sigma _2)\) with respect to \(\mathcal S\) is
where games \(\mathrm { Real}_{\varSigma _1, \mathcal D} \) and \(\mathrm {Ideal}_\mathrm{\Sigma _2, \mathcal S, D}\) are defined in Fig. 1. We say \(\varSigma _1\) is indifferentiable from \(\varSigma _2\), if there exists an efficient simulator \(\mathcal{S}\) such that for any probabilistic polynomial time differentiator \(\mathcal{D}\), the advantage above is negligible. Moreover, we say \( \varSigma _1\) is weakly indifferentiable from \(\varSigma _2\), if for any probabilistic polynomial time differentiator \(\mathcal{D}\), there exists an efficient simulator \(\mathcal {S_D}\) such that the advantage above is negligible.
In the rest of the paper, we also use the notations in [2] and consider the definition above to two systems with interfaces as:
where \(\mathcal {F}_1\) and \(\mathcal {F}_2\) are two ideal objects sampled from their distributions and \(\mathrm {C}^{\mathcal {F}_1}\) is a construction of \(\mathcal {F}_2\) by calling \(\mathcal {F}_1\).
Next, we recall composition theorem for indifferentiability. In [20], MRH give out the composition theorem for indifferentiability, and then Ristenpart, Shacham and Shrimpton (RSS) [22] propose a game-based version for the theorem.
Theorem 2
(Indifferentiability Composition [2, 22]). Let \(\mathrm \Sigma _1 := (\mathrm {C}^{\mathcal {F}_1}, \mathcal {F}_1)\) be a system that is indifferentiable from \(\mathrm \Sigma _2 := (\mathcal {F}_2, \mathcal {F}_2)\) along with simulator \(\mathcal{S}\). Let \(\mathcal G\) be a single-stage game. Then for any adversary \(\mathcal{A}\), there exists an adversary \(\mathcal B\) and a differentiator \(\mathcal D\) such that
However, RSS prove that the composition theorem above does not extend to multi-stage games as the simulator has to keep the local state for consistency. While, Barbosa and Farshim [2] observe that if allowing some relaxations on the games, we could rewrite some multi-stage games as equivalent to single-stage games. Essentially, for an n-adversary game \(\mathcal {G}_n^{C^\mathcal{F}, \mathcal {A}_1, \ldots , \mathcal {A}_n}\), if only one adversary (say \(\mathcal {A}_1\)) can call the ideal objects \(\mathcal F\) directly and the rest can only call \(C^\mathcal{F}\), then \(\mathcal {G}_n\) can be rewritten as a single-stage game, because the game \(\mathcal {G}_n\) itself, of course, has access to \(C^\mathcal{F}\). Then in [2], BF formalize this observation in the following theorem.
Theorem 3
(Multi-stage Game Composition [2]). Let \(\mathrm \Sigma _1 := (\mathrm {C}^{\mathcal {F}_1}, \mathcal {F}_1)\) be a system that is indifferentiable from \(\mathrm \Sigma _2 := (\mathcal {F}_2, \mathcal {F}_2)\) along with simulator \(\mathcal{S}\). Let \(\mathcal {G}\) be an n-adversary game and \(\mathcal{A}:= (\mathcal{A}_1, \ldots , \mathcal{A}_n)\) be a n-tuple of adversaries where \(\mathcal{A}_1\) can access \(\mathcal {F}_1\) but \(\mathcal{A}_i\) (\(i>1\)) can only access \(\mathrm {C}^{\mathcal{F}_1}\). Then there is an n-adversary \(\mathcal{B}\) and a differentiator \(\mathcal D\) such that
Remark. Barbosa and Farshim [2] give a strong motivation for the relaxation imposed on the class of games above. To our best of knowledge, the related-key attack (key-dependent message attack) game is not known to be equivalent to any single-stage game. As a result, it would be insufficient to prove a system is related-key attack secure as follows: 1) there is another system, say \(\mathrm \Sigma _2\), such that \(\mathrm \Sigma _1\) is indifferentiable from \(\mathrm \Sigma _2\); 2) \(\mathrm \Sigma _2\) is related-key attack secure. However, if allowing the relaxation, the proof follows trivially, hence from a practical point of view (by adding this specific relaxation on games), composition extends well beyond 1-adversary games.
3 Indifferentiable NIKE
In this section, we propose the notion of “ideal NIKE” and then build an indifferentiable non-interactive key exchange scheme from simpler ideal primitives and a standard-model NIKE scheme.
3.1 What Is Ideal NIKE?
In this part we give the rigorous description of ideal NIKE, formally:
Definition 4
(Ideal NIKE). Let \(\mathcal X, Y, W\) be three sets such that \(|\mathcal {X}|\ge 2^{\omega (\log \lambda )}, |\mathcal {Y}|\ge 2^{\omega (\log \lambda )}, |\mathcal {W}| \ge 2^{\omega (\log \lambda )}\), \(|\mathcal {X}| \le |\mathcal {Y}|\) and \(|\mathcal {X}| \times |\mathcal {Y}| \le |\mathcal {W}|\). We denote \(\mathcal{F}[\mathcal {X} \rightarrow \mathcal {Y}]\) as the set of all injections that map \(\mathcal X\) to \(\mathcal Y\) and \(\mathcal{G}[\mathcal {X} \times \mathcal {Y} \rightarrow \mathcal {W} ]\) as the set of the functions that map \(\mathcal {X}\times \mathcal {Y}\) to \(\mathcal W\). We define \(\mathcal {T}\) as the set of all function pairs (F, G) such that: 1) \(F \in \mathcal {F}, G \in \mathcal{G}\); 2) \(\forall x, y \in \mathcal {X}, G(x, F(y)) = G(y, F(x) )\); 3) \(G(x_1, y_1) = G(x_2, y_2)\Rightarrow (x_1 = x_2 \wedge y_1 = y_2) \vee (y_1 = F(x_2)\wedge y_2 = F(x_1))\).
We say that a NIKE scheme  , associated with secret key space \(\mathcal X\), public key space \(\mathcal Y\) and shared key space \(\mathcal W\), is an ideal NIKE if \((\mathsf {NIKE{.}KEYGEN, NIKE{.}SHAREDKEY})\) is sampled from \(\mathcal T\) uniformly.
, associated with secret key space \(\mathcal X\), public key space \(\mathcal Y\) and shared key space \(\mathcal W\), is an ideal NIKE if \((\mathsf {NIKE{.}KEYGEN, NIKE{.}SHAREDKEY})\) is sampled from \(\mathcal T\) uniformly.
It’s trivial to note that, due to an information-theoretic argument, an ideal NIKE achieves related-key attack security, leakage-resiliency and so forth. Next, we show how to construct an indifferentiable NIKE scheme from simpler primitives.
3.2 Construction
In this section, we build an indifferentiable NIKE scheme from simpler ideal primitives (namely random oracles and ideal ciphers) along with a standard-model (that is, non-ideal) NIKE scheme.
Building Blocks. Our scheme consists of several building blocks:
-
A standard-model NIKE scheme \(\mathsf {\Pi }_{\mathsf {SM-NIKE}} = (\mathsf {keygen}, \mathsf {sharedkey})\) with secret key space \(\mathcal {X}\), public key space \(\mathcal {Y}\), and shared key space \(\mathcal {Z}\);
-
\(H_0:= \{0,1\}^* \rightarrow \mathcal {X}\) is a random oracle whose co-domain matches the secret key space of \(\varPi \).
-
\(H_1 := \{0,1\}^* \rightarrow \mathcal {W}\) is a random oracle, where \(|\mathcal {X}| \times |\mathcal {Y}| \le |\mathcal {W}| \);
-
\(P:= \mathcal {Y} \rightarrow \mathcal {Y} \) is a random permutation on the public key space of \(\varPi \), and \(P^{-1}\) is P’s inverse.
Note that, the random permutations typically operate on bit strings, which means \(\mathcal {Y}=\{0,1\}^n\) for some natural number \(n \ge \omega (\log \lambda )\). Moreover, the shared key space in the standard model NIKE \(\mathcal Z\) and in our construction \(\mathcal W\) might be not equivalent, because it’s unnecessarily correct that \(|\mathcal X| \times |\mathcal Y| \le |\mathcal Z|\). And if not, then setting \(\mathcal {W} = \mathcal {Z}\) would give a differentiator directly, by just checking whether \(|\mathcal X| \times |\mathcal Y| \le |\mathcal W|\).
Construction. Now we are ready to build an indifferentiable NIKE scheme, denoted as \(\mathsf {\Pi }_{\mathsf {NIKE}} = (\mathsf {NIKE{.}KEYGEN, NIKE{.}SHAREDKEY})\), from the building blocks above. Formally,
-
\(\mathsf {NIKE{.}KEYGEN}(\mathsf {SK}){:}\) Given input \(\mathsf {SK}\), the algorithm runs \(\mathsf {keygen}(H_0(\mathsf {SK}) )\), and outputs the public key \(\mathsf {PK} = P^{-1}(\mathsf {keygen}(H_0(\mathsf {SK})) ) \);
-
\(\mathsf {NIKE{.}SHAREDKEY}(\mathsf {PK}_1, \mathsf {SK}_2){:}\) Given inputs \( (\mathsf {PK}_1, \mathsf {SK}_2)\), the algorithm computes \(\mathsf {PK}_2 = \mathsf {NIKE{.}KEYGEN}(\mathsf {SK}_2 )\) and \(\mathsf {sharedkey}(P( \mathsf {PK}_1 ), H_0(\mathsf {SK}_2) )\). If \(\mathsf {PK}_1 \le \mathsf {PK}_2\), then it outputs the shared key as
$$\begin{aligned} \mathsf {SHK} = H_1 ( \mathsf {PK}_1, \mathsf {PK}_2, \mathsf {sharedkey}(P( \mathsf {PK}_1 ), H_0(\mathsf {SK}_2) ) ), \end{aligned}$$else, it outputs
$$\begin{aligned} \mathsf {SHK} = H_1 ( \mathsf {PK}_2, \mathsf {PK}_1, \mathsf {sharedkey}(P( \mathsf {PK}_1 ), H_0(\mathsf {SK}_2) ) ). \end{aligned}$$
Correctness of the scheme easily follows, and what’s more interesting is its indifferentiability. Next, we prove our scheme is indifferentiable from an ideal NIKE. Before that, we first specify the security properties of the standard-model NIKE.
Property 1
Semi-active unpredictable shared key. We say the shared key, for a NIKE scheme, is semi-active unpredictable, if there is \(\epsilon _1\) such that for any PPT adversary \(\mathcal A\), the advantage
where \(\mathsf {pk}_i = \mathsf {keygen}(\mathsf {sk}_i), \mathsf {sk}_i \leftarrow \mathcal {X}\) and \(\mathcal {O}_i\) is a predicate oracle such that takes \((\mathsf {pk_i, shk})\) as input and outputs a bit (the public key \(\mathsf {pk}\) here might be malicious). Concretely, the oracle \(\mathcal {O}_i\) outputs “1” iff \(\mathsf {shk} = \mathsf {sharedkey}(\mathsf {sk_i, pk})\). This is the standard security game for NIKE schemes against active adversary, except that we relax the notion on two pieces: 1) we only require unpredictability of the shared key, rather than indistinguishability from random; 2) the oracles take both public key \(\mathsf {pk}\) and shared key \(\mathsf {shk}\) as input and tell whether \(\mathsf {shk}\) is a valid shared key, rather than taking the public key \(\mathsf {pk}\), and outputting the corresponding shared key \(\mathsf {shk}\).
The next two properties are mild additional security properties that are not usually required for NIKE schemes, but are achieved by most natural schemes. We require these properties in order to prove the ideal security of our construction.
Property 2
entropic shared keys. We say the shared key, for a NIKE scheme is entropic, if there is \(\epsilon _2\) s.t. for any PPT adversary \(\mathcal A\), the advantage
Note that the entropic shared keys property tells us that if the adversary only knows one public key (even it’s chosen by the adversary), it cannot predict the shared key if the other secret key is random and hidden. In other words, this property guarantees that there is no way to make the shared key have low min-entropy.
Property 3
pseudorandom public keys. We say the public key, for a NIKE scheme, is pseudorandom, if there is \(\epsilon _3\) s.t. for any PPT adversary \(\mathcal A\), the advantage
where \(\mathsf {sk} \leftarrow \mathcal {X}, R \leftarrow \mathcal {Y}\). We immediately observe that as \(\mathcal {Y}=\{0,1\}^n\), our standard-model NIKE must have public keys that are pseudorandom bit strings. And we say a NIKE scheme is \(\mathsf {Good}\) if it satisfies the three properties above.
Theorem 5
(Indifferentiable NIKE). \(\mathsf {\Pi }_{\mathsf {NIKE}}\) is indifferentiable from an ideal NIKE if \(\mathsf {\Pi }_{\mathsf {SM-NIKE}}\) is \(\mathsf {Good}\). More precisely, there exists a simulator \(\mathcal {S}\) such that for all \((q_{H_0}, q_{H_0}, q_{H_0}, q_{H_0})\)-query PPT differentiator \(\mathcal {D}\) with \(q_{H_0}+q_{P}+q_{P^{-1}}+q_{H_1} \le q\), we have
The simulator makes at most q queries to its oracles.
Proof Sketch. According to the definition of indifferentiability, we immediately observe that any PPT adversary has two honest interfaces (\(\mathsf {NIKE{.}KEYGEN}\), \(\mathsf {NIKE{.}SHAREDKEY}\)) (below we will denote \(\mathsf {(NKG, NSK)}\) for ease) and four adversarial interfaces (\(H_0, P, P^{-1}, H_1\)). Therefore, we need to build an efficient simulator \(\mathcal S\) that can simulate the four adversarial interfaces \(H_0, P, P^{-1}\) and \(H_1\) properly, which means, for any PPT differentiator \(\mathcal D\), the view of \(\mathcal D\) in the real game is computationally close to the view in the ideal game. In the following, we illustrate the description of our simulator (similar form as in [2]) in Fig. 2 and then we give the high-level intuition of our proof strategy (here we only give the proof sketch and the intuition of the simulator, and please refer to [27] for full details).
Simulator for NIKE in terms of four sub-simulators associated with two oracles \((\mathsf {NKG, NSK})\). These four sub-simulators share four tables (\(T_{H_0}, T_{P}, T_{P^{-1}}, T_{H_1}\)) as joint state (which are initialized empty). The commands, e.g. “\(\exists (\mathsf {SK, sk, pk, PK}) \in T_{H_0}\)”, go through the table in some well-defined order.
We immediately observe that, our simulator makes at most q queries to \((\mathsf {NKG, NSK})\), and it keeps four tables and the size of each table is at most q, referring to \(\mathcal S\) is efficient. In the following, we present the intuitive idea that why \(\mathcal S\) works. Note that, in the real game, \(H_0, H_1\) are random oracles, P is a random permutation associated with its inverse \(P^{-1}\). Hence, the responses of a proper simulator should follow the following rules:
-
1.
The responses of \(H_0,H_1\) are computational close to uniform distribution;
-
2.
The responses of \(P, P^{-1}\) are computational close to a random permutation;
-
3.
There do not exist \( (\mathsf {PK_1\ne PK_2}), (\mathsf {pk_1 \ne pk_2})\) such that \(P^( \mathsf {PK_1}) = P^( \mathsf {PK_2}) \) or \( P^{-1}( \mathsf {pk_1}) = P^{-1}( \mathsf {pk_2}) \);
-
4.
\(\mathsf {NKG}(\mathsf {SK}) = P^{-1}(\mathsf {keygen}(H_0(\mathsf {SK})) ) \);
-
5.
\(\mathsf {NSK}(\mathsf {SK_1, PK_2}) = \mathsf {NSK}(\mathsf {SK_2, PK_1}) = H_1(\{\mathsf {PK_1, PK_2}\}\)Footnote 6, \(\mathsf {sharedkey}(\mathsf {sk_1, pk_2})) \).
Next, we illustrate why and how \(\mathcal S\) achieves these five rules.
Rule 1. Easy to note that the response of any \(H_0\) query (\(H_0(\mathsf {SK})\)) is well-formed. Roughly, \(\mathcal S\) responds to it using \(T_{H_0}\), \(T_{P}\) (the second term of the corresponding tuple) or with a random string \(\mathsf {sk} \in \mathcal X\). Moreover, note that the second term in every tuple from table \(T_{H_0}\) or \(T_{P}\) is uniformly sampled, referring to \(H_0(\mathsf {SK})\) is uniformly distributed. For \(H_1\) query, say \(H_1(\mathsf {PK_1, PK_2, shk})\), the simulator responds to it with either \(\mathsf {NSK(SK_1, PK_2)}\) (if the tests pass) or a random string \(\mathsf {w} \in \mathcal W\). And we note that \((\mathsf {NKG, NSK})\) is an ideal NIKE, which means that \(\mathsf {NSK(SK_1, PK_2)}\) is uniformly distributed.
Rule 2. For P query, say \(P(\mathsf {PK})\), the simulator responds to the query in four cases: 1) using \(T_P\); 2) using \(T_{P^{-1}}\); 3) using \(T_{H_0}\); 4) randomly sampling a secret key and outputting the corresponding public key. Easy to note that, in case 1, 3, and 4, \(\mathcal S\) always returns a random public key, and due to the pseudo-random public keys, we have that the response is computational close to uniform. For Case 2, note that if \(\mathsf {PK} \in \mathsf {T}_{\mathsf {P}^{\textsf {-1}}} \), then we know that the adversary has made a query \(P^{-1}(\mathsf {pk})\) previously. For that \(P^{-1}\) query, \(\mathcal S\) samples \(\mathsf {SK} \in \mathcal X\) and responds to it with \(\mathsf {PK} = \mathsf {NKG(SK)}\). As \((\mathsf {NKG, NSK})\) is an ideal NIKE, we have that \(\mathsf {PK}\) is close to uniform in \(\mathcal Y\) and the response of \(P^{-1}(\mathsf {pk})\) is well distributed. As a result, when making a query \(P(\mathsf {PK})\), \(\mathsf {pk}\) is the proper answer. Moreover, \(P^{-1}\) is P’s inverse, which means the responses of \(P^{-1}\) are also well-distributed.
Rule 3. This rule indicates that P and \(P^{-1}\) must be bijective. For \(\mathcal S\), note that there are four bad cases that break the rule:
-
1.
\(\mathsf {pk}\)-collision: \(\mathcal {A}\) makes a query \(P(\mathsf {pk^*})\) with response \(\mathsf {PK_1^*}\), and then it makes another query \(P^{-1}(\mathsf {PK_2^*})\) with response \(\mathsf {pk^*}\);
-
2.
\(\mathsf {PK}\)-collision: \(\mathcal {A}\) makes a query \(P(\mathsf {PK^*})\) with response \(\mathsf {pk_1^*}\), and then it makes another query \(P(\mathsf {pk_2^*})\) with response \(\mathsf {NKG(SK^*)} = \mathsf {PK^*}\);
-
3.
Guessed-\(H_0(\mathsf {SK})\)-on-\(\mathsf { pk^*}\): adversary makes a query \(P^{-1}(\mathsf {PK^*})\) with response \(\mathsf {keygen(sk^*)}\), and \(\mathcal A\) also makes a query \(H_0(\mathsf {SK})\) such that \(\mathsf {keygen}(H_0(\mathsf {SK^*})) = \mathsf {keygen(sk^*)}\) and \(\mathsf {NKG(SK)} \ne \mathsf {PK^*}\);
-
4.
Guessed-\(\mathsf {SK^*}\)-on-\(\mathsf {PK^*}\): \(\mathcal {A}\) makes a query \(P(\mathsf {pk^*})\) with response \(\mathsf {NKG}(\mathsf {SK^*})\), and \(\mathcal {A}\) also makes a query \(H_0(\mathsf {SK^*})\) such that \(\mathsf {keygen}(H_0(\mathsf {SK^*})) \ne \mathsf {pk^*}\).
For case 1, due to pseudorandom random public keys, it occurs with negligible probability. For case 2, as \(\mathsf {NKG}\) is ideal NIKE oracle, collision never happens except with negligible probability.
For case 3, as the simulator samples \(\mathsf {sk^*}\), which is independent of \(\mathcal A\)’s view, the probability of \(\mathcal A\) outputs a proper \(\mathsf {SK}\) \((H_0(\mathsf {SK}) = \mathsf {sk^*}\)) is bounded by pseudorandom public keys. Analogously, in case 4 \(\mathcal A\) cannot guess \(\mathsf {SK^*}\) correctly except for negligible probability.
Rule 4. Note that if the adversary first makes a query \(H_0({\mathsf {SK}})\), then the equation holds for certain when it requests \(P^{-1}\). Hence, the only chance that \(\mathcal A\) violates this rule is case 3 in Rule 3 occurs, referring to Rule 4 holds as long as Rule 3 holds.
Rule 5. Firstly, we note that the responses of \(H_1\) queries are independent of the ones of \(H_0, P, P^{-1}\) queries, and the only consistency \(\mathcal S\) has to preserve is the equation in this rule. Immediately observe that, if and only if, the inputs of the \(H_1\) are in a good form (say, \(\mathsf {PK_1} = \mathsf {PK_2}\) and \(\mathsf {shk}\) is a valid shared key of \(\mathsf {pk_1}\) and \(\mathsf {pk_2}\)), the response should be consistent to \(\mathsf {NSK}\)-oracle (if the inputs are not in a good form, then the response is independent of \(\mathsf {NSK}\)-oracle with high probability).
Easy note that, except for the last case (associated with underline), \(\mathcal S\) responds to \(H_1\) queries properly: \(\mathcal S\) calls \(\mathsf {NSK}\)-oracle when the input is within good form and otherwise returns a string \(\mathsf {w} \in \mathcal W\). While, for the last one, the simulator just responds with \(\mathsf {w}\) without checking whether the inputs are good or not. Hence, we hope that, for the last case, either the inputs are not in a good form or \(\mathsf {NSK(SK_1, PK_2)}\) is independent of \(\mathcal A\)’s view. In fact, there are three bad cases that might break it:
-
1.
A known secret key and another random public key: \(\mathcal A\) chooses \(\mathsf {sk_1}\) and makes a query \(P^{-1}(\mathsf {keygen(sk_1}))\) with response \(\mathsf {PK_1}= \mathsf {NKG}(\mathsf {SK_1})\), while \(\mathsf {PK_2} \notin T_{P}\cup T_{P^{-1}} \cup T_{H_0}\);
-
2.
Two known secret keys in \(T_{P^{-1}}\): Adversary chooses \(\mathsf {sk_1, sk_2}\) and makes queries \(P^{-1}(\mathsf {keygen(sk_1)}), P^{-1}(\mathsf {keygen(sk_2}))\) with responses \(\mathsf {NKG}(\mathsf {SK_1}), \mathsf {NKG}(\mathsf {SK_2})\);
-
3.
Two known public keys without secret key keys: \(\mathcal A\) chooses \(\mathsf {SK_1, SK_2}\) and makes queries \(P(\mathsf {NKG(SK_1)}), P(\mathsf {NKG(SK_2)})\) with responses \(\mathsf {pk_1} = \mathsf {keygen}(\mathsf {sk_1}), \mathsf {pk_2} = \mathsf { keygen(sk_2)}\).
For case 1, we note that \(\mathsf {PK_2}\) never appears in tables \(T_P, T_{P^{-1}}\) and \(T_{H_0}\), which means \(P(\mathsf {PK_2} ) \) is independent of \(\mathcal A\)’s view. Hence, the probability that \(\mathsf {shk}\) is a valid shared key is bounded by the entropic shared keys (illustrated in Attack 6), which is negligible.
For case 2, we observe that \(\mathcal A\) chooses the two secret keys itself; hence \(\mathsf {shk}\) would be a valid shared key if \(\mathcal A\) wants. However, \(\mathsf {SK_1}\) and \(\mathsf {SK_2}\) are independent of \(\mathcal A\)’s view, which refers to that \(\mathsf {NSK}(\mathsf {SK_1, PK_2})\) is also independent of \(\mathcal A\)’s view.
For case 3, \(\mathcal A\) knows \(\mathsf {pk_1}\) and \(\mathsf {pk_2}\) while the corresponding secret keys \(\mathsf {sk_1}\) and \(\mathsf { sk_2}\) are independent of \(\mathcal A\)’s view. Meanwhile, the adversary might implement \((\mathsf {NKG}, \mathsf {NSK})\) into oracles and use those oracles as an additional helper to predict the shared key (illustrated in Attack 7). Fortunately, \(\mathsf {(NKG, NSK)}\) is an ideal NIKE; thus the only thing the adversary can do is equality test, which means the oracles adversary implements is the best helper it can count on. Hence, the probability that \(\mathsf {shk}\) is a valid shared key is bounded by the semi-active unpredictable shared keys.
4 Indifferentiable Public Key Encryption
In this section, we propose the notion of “ideal PKE” and then build an indifferentiable public key encryption scheme from ideal NIKE and random oracles. Roughly, our strategy consists of two steps: first, we construct an indifferentiable deterministic public key encryption (DPKE) from an ideal NIKE, and then build an indifferentiable PKE from an ideal DPKE.
4.1 What Is Ideal PKE?
In this part, we give the rigorous description of ideal PKE, formally:
Definition 6
(Ideal PKE). Let \(\mathcal{X, Y, M, R, C}\) be five sets such that: 1) \(|\mathcal {X}|\ge 2^{\omega (\log \lambda )}, |\mathcal {Y}|\ge 2^{\omega (\log \lambda )}, |\mathcal {R}|\ge 2^{\omega (\log \lambda )}\) and \(|\mathcal {C}| \ge 2^{\omega (\log \lambda )}\); 2) \(|\mathcal {X}| \le |\mathcal {Y}|\); 3) \(|\mathcal {Y}| \times |\mathcal {M}| \times |\mathcal {R} | \le |\mathcal {C}|\). We denote \(\mathcal {F}[\mathcal {X} \rightarrow \mathcal {Y}]\) as the set of all injections that map \(\mathcal {X}\) to \(\mathcal {Y}\); \(\mathcal {E} [\mathcal {Y}\times \mathcal {M} \times \mathcal {R} \rightarrow \mathcal {C}] \) as the set of all injections that map \(\mathcal {Y}\times \mathcal {M} \times \mathcal {R}\) to \(\mathcal {C}\) and \(\mathcal {D} [\mathcal {C} \times \mathcal {X} \rightarrow \mathcal {M} \cup \perp ]\) as the set of all functions that map \(\mathcal {X}\times \mathcal {C}\) to \(\mathcal {M}\cup \perp \). We define \(\mathcal {T}\) as the set of all function tuples (F, E, D) such that:
-
\(F \in \mathcal {F}, E \in \mathcal {E}\) and \(D \in \mathcal {D}\);
-
\(\forall x \in \mathcal {X}, m \in \mathcal {M}\) and \( r \in \mathcal {R} \), \(D (x, E(F(x), m, r ) ) = m\);
-
\( \forall x \in \mathcal {X}, c \in \mathcal {C}\), if there is no \((m, r) \in \mathcal {M} \times \mathcal {R}\) such that \(E(F(x), m, r) = c \), then \(D(x, c) = \perp \).
We say that a PKE scheme \(\mathsf {\Pi }_{\mathsf {PKE}} = (\mathsf {PKE{.}KEYGEN, PKE{.}ENC, PKE{.}DEC } )\), associated with secret key space \(\mathcal {X}\), public space \(\mathcal {Y}\), message space \(\mathcal {M}\), nonce space space \(\mathcal {R}\), and ciphertext space \(\mathcal {C}\), is an ideal PKE if \(\varPi _{\mathsf {PKE}}\) is sampled from \(\mathcal {T}\) uniformly. Moreover, if the nonce space is empty, then we say such a scheme is an ideal DPKE.
4.2 Construction for Deterministic PKE
In this section, we build an indifferentiable deterministic PKE (DPKE) from simpler ideal primitives (namely random oracles and ideal ciphers) along with an ideal NIKE. We firstly present our first attempt of the construction and then illustrate a differentiator to break it (this attack also indicates a difficulty of building indifferentiable PKE). Next, we give our solution to get rid of the attack and establish the proof.
First Attempt to Build an Indifferentiable DPKE. Given an ideal NIKE \(\mathsf {\Pi }_{\mathsf {NIKE}}\), a natural way to build an indifferentiable DPKE is the following: 1) convert this ideal NIKE into a PKE scheme; 2) apply the Fujisaki-Okamoto transformation [15], which combines with a random oracle to give at least CCA-2 security. The hope is that this transformation would give us an indifferentiable DPKE. Specifically, let \(\mathsf {\Pi _{NIKE}} = (\mathsf {NKG, NSK} )\) be an ideal NIKE, associated with secret key space \(\mathcal {X}\), public key space \(\mathcal {Y}\) and shared key space \(\mathcal {Z}\), and we denote \(\mathsf {sk, pk, shk}\) to be the secret key, public key and shared key of \(\mathsf {\Pi }_{\mathsf {NIKE}}\), respectively. For an easy exposition, we always denote the inputs of component primitives (for instance, in the standard model NIKE in Sect. 3 or the ideal NIKE in this section) as the lower-case and inputs of the target primitives as the upper-case. Let \(\mathsf {H_0, H_1} := \{0,1\}^* \rightarrow \mathcal {X}; \mathsf {H_2} := \{0,1\}^* \rightarrow \mathcal {Z}; \mathsf {H_3} := \{0,1\}^* \rightarrow \mathcal {M}\), then applying FO-transform, we have the following DPKE scheme: \(\mathsf {\Pi _{DPKE}} = (\mathsf {DPKE{.}KEYGEN, DPKE{.}ENC,} \mathsf {DPKE{.}DEC})\).
-
\(\mathsf {DPKE{.}KEYGEN}(\mathsf {SK})\): On inputs secret key \(\mathsf {SK}\), the algorithm outputs public key \(\mathsf {PK} = \mathsf {NKG}(H_0(\mathsf {SK} ))\);
-
\(\mathsf {DPKE{.}ENC}(\mathsf {PK,M} )\): On inputs public key \(\mathsf {PK}\) and message \(\mathsf {M}\), the algorithm computes \(\delta = H_2(\mathsf {PK||M})\), and outputs ciphertext \(\mathsf {C}\) as
$$\begin{aligned} \mathsf {C} = (\mathsf {C_1, C_2,C_3}) = (\mathsf {NKG}(H_1(\mathsf {PK||M}) ), \delta \oplus \mathsf {NSK}( \mathsf {PK}, H_1(\mathsf {PK||M} ) ), H_3(\mathsf {PK}, \delta ) \oplus \mathsf {M} ); \end{aligned}$$ -
\(\mathsf {DPKE{.}DEC}(\mathsf {SK, C})\): On inputs secret key \(\mathsf {SK}\) and ciphertext \(\mathsf {C} = (\mathsf {C_1, C_2, C_3})\), the algorithm computes:
$$\begin{aligned}&\mathsf {PK} = \mathsf {DPKE{.}KEYGEN}(\mathsf {SK}); \mathsf {A_1} = \mathsf {NSK}(\mathsf {C_1}, H_0(\mathsf {SK}) ); \\&\mathsf {A_2} = \mathsf {C_2} \oplus \mathsf {A_1}; \mathsf {A_3} = \mathsf {C_3} \oplus H_3(\mathsf {PK}||\mathsf {A_2}). \end{aligned}$$Then it tests whether \(\mathsf {C} \overset{?}{ = } \mathsf {DPKE{.}ENC(PK||M)} \). If yes, then outputs \(\mathsf {A_3}\), else aborts.
Correctness easily follows, but this scheme is not indifferentiable. Next we present a differentiator to break it.
Differentiator for FO Transform. Due to definition, \(\mathcal {D}\) has three honest interfaces (\(\mathsf { DPKE{.}KEYGEN, DPKE{.}ENC, DPKE{.}DEC}\)) (below, we will denote (\(\mathsf { DKG, DE, DD}\)) for short) and six adversarial interfaces (\(H_0, H_1, H_2, H_3,{\mathsf {Pg}}{} \mathsf {NKG}, \mathsf {NSK} \)), and we build \(\mathcal {D}\) as in Fig. 3:
We immediately observe that, in the real game, \(\mathsf {A}\) and \((\mathsf {B_1,B_2,B_3})\) are the corresponding public key and ciphertext, respectively. Moreover, due to \( \mathsf {\Pi }_{\mathsf {NIKE}}\)’s correctness, we have
which means that \(\mathcal {D}\) always outputs 1. However, in the ideal game, the simulator knows nothing of queries to the honest interfaces, and the only information it has is: \((\mathsf {SK, A, B_1, B_2})\) (other information such like  and
and  are simulated by \(\mathcal S\) itself). Therefore, without decryption oracle, \(\mathsf {M}\) is independent of simulator’s view. And the decryption oracle always aborts except \(\mathcal S\) hands in a valid ciphertext, which consists of three elements \((\mathsf {B_1, B_2, B_3} )\). Moreover, in the ideal world, the honest interface \(\mathsf {DPKE{.}ENC}\) is a random injection, hence \( \Pr [ \mathcal {S} \ \hbox {outputs a valid} \ \mathsf {B_3} ] \le \frac{\mathsf {poly}(\lambda )}{|\mathcal {M}|}. \)
are simulated by \(\mathcal S\) itself). Therefore, without decryption oracle, \(\mathsf {M}\) is independent of simulator’s view. And the decryption oracle always aborts except \(\mathcal S\) hands in a valid ciphertext, which consists of three elements \((\mathsf {B_1, B_2, B_3} )\). Moreover, in the ideal world, the honest interface \(\mathsf {DPKE{.}ENC}\) is a random injection, hence \( \Pr [ \mathcal {S} \ \hbox {outputs a valid} \ \mathsf {B_3} ] \le \frac{\mathsf {poly}(\lambda )}{|\mathcal {M}|}. \)
Our Solution. To prevent the attack above, the only hope is \(\mathcal S\) can always output a valid ciphertext itself. Our trick is, instead of using random oracles, we use an ideal cipher model P, with inverse. Specifically, let \(\mathcal {Z} = \mathcal {Y} \times \mathcal {M}\) (we specify the shared key space of \(\mathsf {\Pi }_{\mathsf {NIKE}}\) to be \(\mathcal {Y} \times \mathcal {M}\) and \(|\mathcal {X}| \le |\mathcal {M}|\)), and \(P := \mathcal {Z} \rightarrow \mathcal {Z}\). Now, we denote \(\delta = P(\mathsf {PK}||\mathsf {M})\), and modify the ciphertext as \(C = (\mathsf {NKG}(\mathsf {H_1}(\mathsf {PK||M}) ), \delta \oplus \mathsf {NSK}( \mathsf {PK}, \mathsf {H_1}(\mathsf {PK||M}) ) ) )\). Formally:
-
\(\mathsf {DPKE{.}KEYGEN}(\mathsf {SK})\): On inputs secret key \(\mathsf {SK}\), the algorithm outputs public key \(\mathsf {PK} = \mathsf {NKG}(H_0(\mathsf {SK} ))\);
-
\(\mathsf {DPKE{.}ENC}(\mathsf {PK,M} )\): On inputs public key \(\mathsf {PK}\) and message \(\mathsf {M}\), the algorithm computes \(\delta = P(\mathsf {PK||M})\), and outputs ciphertext \({\mathsf {C}}\) as
$$ \mathsf {C} = (\mathsf {C_1, C_2}) = (\mathsf {NKG}(H_1(\mathsf {PK||M}) ), \delta \oplus \mathsf {NSK}( \mathsf {PK}, \mathsf {H_1(PK,M)} ) ); $$ -
\(\mathsf {DPKE{.}DEC}(\mathsf {SK, C})\): On inputs secret key \(\mathsf {SK}\) and ciphertext \(\mathsf {C} = (\mathsf {C_1, C_2})\), the algorithm computes:
$$\begin{aligned}&\mathsf {PK} = \mathsf {DPKE{.}KEYGEN}(\mathsf {SK}); \mathsf {A_1} = \mathsf {NSK}(\mathsf {C_1}, H_0(\mathsf {SK}) ); \\&\mathsf {A_2} = \mathsf {C_2} \oplus \mathsf {A_1}; \mathsf {A_3} = P^{-1}(A_2), \mathsf {A_4} = \mathsf {A_3} / \mathsf {PK} . \end{aligned}$$Then it tests whether \(\mathsf {C} \overset{?}{ = } \mathsf {DPKE{.}ENC(A_3)} \). If yes, then outputs \(\mathsf {A_4}\)Footnote 7, else aborts.
In our new setting, we immediately observe that the ciphertext only consists of two elements, which means \(\mathcal S\) can always hand in the valid ciphertext to the decryption oracle. As a result, our new scheme prevents the attack above. Apparently, this is only an evidence that our new scheme prevents this specific differentiator. And to prove it’s an indifferentiable DPKE, we need to show that our scheme can prevent all kind of efficient differentiators.
Theorem 7
(Indifferentiable DPKE). \(\mathsf {\Pi }_{\mathsf {DPKE}}\) is indifferentiable from an ideal DPKE if \(\mathsf {\Pi }_{\mathsf {NIKE}} = (\mathsf {NKG, NSK})\) is an ideal NIKE. More precisely, there exists a simulator \(\mathcal {S}\) such that for all \((q_{H_0}, q_{H_1}, q_{P}, q_{P^{-1}}, q_\mathsf {NKG}, q_\mathsf {NSK})\)-query PPT differentiator \(\mathcal {D}\) with \(q_{H_0}+q_{H_1}+q_{P}+q_{P^{-1}}+q_{\mathsf {NKG}}+q_\mathsf {NSK}\le q\), we have
The simulator makes at most \(q^2\) queries to its oracles.
4.3 Construction for PKE
In this section, we complete the construction by building an indifferentiable PKE from ideal DPKE and random oracles. Similarly as in Sect. 4.2, we firstly present two attempts and then illustrate the corresponding differentiators to break the schemes. Then we give the modified solution to get rid of those attacks and complete the proof.
First Attempt to Build an Indifferentiable PKE. Immediately to observe that we cannot build our scheme in the trivial way, say, treating the random nonce as part of the message and discarding it in the decryption procedure, because this construction loss the information of the randomness and that would induce a differentiator which trivially tests the validity of the randomness. To prevent it, we again apply the hash technique (\(H_0:= \{0,1\}^* \rightarrow \mathcal R\)); we first hash the nonce and then use the hashed value as the randomness. Specifically,
-
\({\mathsf {PKE{.}KEYGEN} (\mathsf {SK}) = \mathsf {DKG}(\mathsf {SK})}\);
-
 ;
; -
\(\mathsf {PKE{.}DEC}(\mathsf {SK, C} ) \): On inputs a secret key \(\mathsf {SK}\) and a ciphertext \(\mathsf {C}\), the algorithm runs \(\mathsf {DD}(\mathsf {SK, C})\). If \(\mathsf {DD}\) aborts then the algorithm aborts, else let
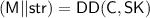 , it outputs \(\mathsf {M}\).
, it outputs \(\mathsf {M}\).
However, the scheme would not achieve indifferentiability if the random oracle is not well-designed, and the following we give out a differentiator to break our first attempt in Fig. 4:
Easy to note that, in real game, \(\Pr [\mathcal {D}=1 ]=1 \). Meanwhile, in ideal game, we claim that, with noticeable probability, the decryption would abort. In fact, the decryption procedure outputs \(\mathsf {M}\) if and only if there exists a nonce \(\mathsf {R} \in \mathcal R\) such that \(H_0(\mathsf {PK, M, R}) = \mathsf {r}\). Moreover, \(\mathsf {R, r} \in \mathcal R \), and \(H_0\) is a random oracle, we have that \( \Pr [ \forall \mathsf {R} \in \mathcal {R}, H_0(\mathsf {PK, M, R} ) \ne r ] \approx 1/e, \) referring to \(\Pr [\mathcal {D} =1 ] \le 1 - 1/e \approx 0.6\).
Our Solution. To prevent this attack, we have to shorten the size of \(H_0\)’s range, to make sure that every element in \(H_0\)’s range has pre-image with high probability. Meanwhile, to make sure the ciphertext space is sufficiently large, we also need to pad some dummy strings. Specifically, let \(\mathsf {\Pi }_{\mathsf {DPKE}}\) be an ideal DPKE, associated with secret key space \(\mathcal X\), public key space \(\mathcal {Y} = \{0,1\}^{n_1}\), message space \(\mathcal {M} = \{0,1\}^{n_2+ 2n_3}\), and ciphertext space \(\mathcal {C}\), and let \(H_0 := \{0,1\}^* \rightarrow \{0,1\}^{n_3}\), where \(n_2 > 0\) and \(n_1, n_3 \ge \omega (\log \lambda )\), then we build our scheme as:
-
\(\mathsf {PKE{.}KEYGEN}(\mathsf {SK}) = \mathsf {DKG}(\mathsf {SK}) \):
-
\(\mathsf {PKE{.}ENC}(\mathsf {PK, M, R})\): On inputs public key \(\mathsf {PK}\), message \(\mathsf {M} \in \{0,1\}^{n_2}\) and nonce \(\mathsf {R} \in \{0,1\}^{2n_3}\), the algorithm outputs ciphertext:
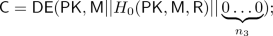
-
\(\mathsf {PKE{.}DEC}(\mathsf {SK,C} )\): On inputs secret key \(\mathsf {SK}\) and ciphertext \(\mathsf {C}\), the algorithm runs \(\mathsf {A} = \mathsf {D}_{\mathsf {DPKE}}(\mathsf {SK,C})\). If \(\mathsf {A} = \perp \) or the last \(n_3\) bits are not \(0^{n_3}\), then it aborts, else the algorithm outputs the first \(n_2\) bits.
Correctness follows easily, and the rest is to show its indifferentiability.
Theorem 8
(Indifferentiable PKE). \(\mathsf {\Pi }_{\mathsf {PKE}}\) is indifferentiable from an ideal PKE if \(\mathsf {\Pi }_{\mathsf {DPKE}} = (\mathsf {DKG, DE, DD})\) is an ideal DPKE. More precisely, there exists a simulator such that for all (\(q_{H_0}, q_{\mathsf {DKG}}, q_{\mathsf {DE}}, q_{\mathsf {DD}}\))-query PPT differentiator \(\mathcal {D}\) with \(q_{H_0}+q_{\mathsf {DKG}}+q_{\mathsf {DE}}+q_{\mathsf {DD}}\le q\), we have
The simulator makes at most \(q^2\) queries to its oracles.
5 Indifferentiable Digital Signatures
In this section, we extend our result to the digital signature scheme. We propose the notion of “Ideal Signature”, and then build an indifferentiable signature scheme from simpler ideal primitives (random oracle model and ideal cipher model) and a stand-model signature scheme.
5.1 What Is “Ideal Signature”?
In this part, we give the rigorous description of ideal signature, formally:
Definition 9
(Ideal Signature). Let \(\mathcal {X, Y, M}, \varSigma \) be four sets such that: 1) \(|\mathcal {X}|\ge 2^{\omega (\log \lambda )}, |\mathcal {Y}|\ge 2^{\omega (\log \lambda )}, |\mathcal {M}|\ge 2^{\omega (\log \lambda )}\) and \( |\varSigma | \ge 2^{\omega (\log \lambda )}\); 2) \(|\mathcal {X}| \le |\mathcal {Y}|\); 3) \(|\mathcal {X}| \times |\mathcal {M}| \le |\varSigma |\). We denote \(\mathcal {F}[\mathcal {X} \rightarrow \mathcal {Y}]\) as the set of all injections that map \(\mathcal {X}\) to \(\mathcal {Y}\); \(\mathcal {S} [\mathcal {X}\times \mathcal {M} \rightarrow \varSigma ] \) as the set of all injections that map \(\mathcal {X}\times \mathcal {M}\) to \(\varSigma \) and \(\mathcal {V} [\mathcal {Y} \times \mathcal {M} \times \varSigma \rightarrow \{0,1\}]\) as the set of all functions that map \(\mathcal {Y}\times \mathcal {M} \times \varSigma \) to a bit. We define \(\mathcal {T}\) as the set of all function tuples (F, S, V) such that:
-
\(F \in \mathcal {F}, S \in \mathcal {S}\) and \(V \in \mathcal {V}\);
-
\(\forall x \in \mathcal {X}, m \in \mathcal {M}\), \(V(F(x), m, S(x, m ) ) =1\);
-
\(\forall x \in \mathcal {X}, m \in \mathcal {M}\) and \(\sigma \in \varSigma \), if \(\sigma \ne \mathsf {sign}(x,m )\), then \(V(F(x), m, \sigma ) =0\);
-
\(\forall x \in \mathcal {X}, m \in \mathcal {M}\) and \(\sigma _1, \sigma _2 \in \varSigma \), \(V(F(x), m, \sigma _1) = V(F(x), m, \sigma _2) = 1\Rightarrow \sigma _1 = \sigma _2 \).
We say that a digital signature scheme \(\mathsf {\Pi }_{\mathsf {Sig}} = (\mathsf {Sig{.}KEYGEN, Sig{.}SIGN, Sig{.}VER} )\), associated with secret key space \(\mathcal {X}\), public key space \(\mathcal {Y}\), message space \(\mathcal {M}\) and signature space \(\varSigma \), is an ideal digital signature, if \(\mathsf {\Pi }_{\mathsf {Sig}}\) is sampled from \(\mathcal {T}\) uniformly.
5.2 Construction
In this section, we build our indifferentiable signature scheme from random oracle model and a standard-model signature scheme.
Difficulty of Building an Indifferentiable Signature. To achieve indifferentiability, we note that the signature \(\sigma \) would be masked by an idealized primitive, say \(\varSigma = P^{-1}(\sigma )\) as above. In the verification algorithm, the scheme inverts \(\varSigma \) and uses \(\sigma \) to proceed. Unfortunately, this P-technique is insufficient here. In fact, given \(\varSigma \) (it is either a valid signature or a random string), the simulator cannot call \(\mathsf {Ver}\) (the ideal signature) for help, as it does not know the public key and message. So the simulator cannot respond to \(P(\varSigma )\) properly. To get rid of this difficulty, we would apply an ideal cipher model \((E, E^{-1})\) instead, where we set \((\mathsf {PK, M})\) as its secret key. How does it help? We note that we force the adversary to hand it the public key and message to the simulator when inverting \(\varSigma \); as a result, the simulator can call \(\mathsf {Ver}\) and simulate \(E(\varSigma )\) properly. Concretely,
Building Blocks. Our scheme will consist of several building blocks:
-
A standard-model signature scheme \(\mathsf {\Pi }_{\mathsf {SM-Sig}} = (\mathsf {keygen, sign, ver} )\) with secret key space \(\mathcal X\), public key space \(\mathcal {Y} = \{0,1\}^{n_1}\), message space \(\mathcal {M} = \{0,1\}^{n_2}\) and signature space \(\mathcal {Z} \subset \{0,1\}^{n_3}\);
-
\(H_0 := \{0,1\}^* \rightarrow \mathcal {X}; H_1 := \{0,1\}^* \rightarrow \mathcal {M}\);
-
\(P:= \{0,1\}^{n_1} \rightarrow \{0,1\}^{n_1} \) is a random permutation and \(P^{-1}\) is P’s inverse,
-
\(E: = \{0,1\}^{n_1+n_2} \times \{0,1\}^{n_3} \rightarrow \{0,1\}^{n_3}\) is an ideal cipher model, where \(\{0,1\}^{n_1+n_2}\) is its key space and \(E^{-1}\) is its inverse.
Construction. Now we are ready to build an indifferentiable signature scheme, denoted as \(\mathsf {\Pi }_{\mathsf {Sig}} = (\mathsf {Sig{.}KEYGEN, Sig{.}SIGN, Sig{.}VER} )\), from the building blocks above. Formally,
-
\(\mathsf {Sig{.}KEYGEN}(\mathsf {SK})\): On inputs secret key \(\mathsf {SK}\), the algorithm outputs public key \(\mathsf {PK} = P^{-1}(\mathsf {keygen}(H_0(\mathsf {SK}) ) )\);
-
\(\mathsf {Sig{.}SIGN}(\mathsf {SK, M} )\): On inputs secret key \(\mathsf {SK}\) and message \(\mathsf {M}\), the algorithm computes \(\mathsf {PK} = \mathsf {Sig{.}KEYGEN}(\mathsf {SK})\) and outputs the signature
$$\begin{aligned} \varSigma = E^{-1}((\mathsf {PK}||\mathsf {M}), \mathsf {sign}( H_0(\mathsf {SK}), H_1(\mathsf {M}) ) ), \end{aligned}$$ -
\(\mathsf {Sig{.}VER}(\mathsf {PK,M}, \varSigma )\): On inputs public key \(\mathsf {PK}\), message \(\mathsf {M}\) and the signature \(\sigma \), the algorithm outputs a bit \(b = \mathsf {ver}(P(\mathsf {PK}), H_1(\mathsf {M}), E( (\mathsf {PK}||\mathsf {M}), \varSigma ) )\).
Correctness easily follows, and the rest is to prove its indifferentiability. Before that, we specify several security properties of the standard-model signature.
Property 1
uniqueness. We say a signature achieves uniqueness, if \(\forall (\mathsf {pk,sk}) \leftarrow \mathsf {keygen}, \mathsf {m} \in \mathcal {M}, \sigma _1, \sigma _2 \in \varSigma \), we have,
Property 2
random-message attack (RMA). We say a signature scheme is RMA-secure if there is \(\epsilon _1\) such that for any PPT adversary \(\mathcal A\), the advantage
where  and \(\mathsf {m^*}\) was not previously signed.
and \(\mathsf {m^*}\) was not previously signed.
Property 3
pseudorandom public key. We say the public key is pseudorandom, if there is \(\epsilon _2\) such that for any PPT adversary \(\mathcal A\), \(r \leftarrow \mathcal {X}, R \leftarrow \mathcal {Y}\).
We say a signature scheme is \(\mathsf {Good}\) if it satisfies the three properties above.
Theorem 10
(Indifferentiable Signatures). \(\mathsf {\Pi }_{\mathsf {Sig}}\) is indifferentiable from an ideal digital signature if \(\mathsf {\Pi }_{\mathsf {SM-Sig}}\) is \(\mathsf {Good}\). More preciously, there exists a simulator \(\mathcal S\) such that for all \((q_{H_0}, q_{H_1}, q_{P}, q_{P^{-1}}, q_{E}, q_{E^{-1}})\)-query PPT differentiator \(\mathcal D\) with \(q_{H_0}+q_{H_1}+q_{P}+q_{P^{-1}}+q_{E}+q_{E^{-1}} \le q\), we have
The simulator makes at most \(q^2\) queries to its oracles.
Notes
- 1.
By the injectivity of \({\mathsf {\MakeUppercase {KEYGEN}}}\), this is still a well-defined function.
- 2.
There are actually several exceptions, for instance, the length-extension attacks against various Merkle-Damgard-based hash functions, such as MD5.
- 3.
By having the random oracle be sufficiently expanding, it will be an injection with high probability.
- 4.
Here, \(\{{\mathsf {\MakeUppercase {PK}}}_1,{\mathsf {\MakeUppercase {PK}}}_2\}\) means the un-ordered set containing \({\mathsf {\MakeUppercase {PK}}}_1\) and \({\mathsf {\MakeUppercase {PK}}}_2\), so that \(\{{\mathsf {\MakeUppercase {PK}}}_1,{\mathsf {\MakeUppercase {PK}}}_2\}=\{{\mathsf {\MakeUppercase {PK}}}_2,{\mathsf {\MakeUppercase {PK}}}_1\}\).
- 5.
One can define a different idealization of PKE where the ideal decryption functionality does output the encryption randomness. However, this stronger functionality corresponds to weaker security guarantees.
- 6.
If \(\mathsf {PK_1 \le PK_2}\), \(\{\mathsf {PK_1, PK_2}\} = (\mathsf {PK_1, PK_2})\), and else \(\mathsf {PK_1 \le PK_2} =(\mathsf {PK_2, PK_1})\).
- 7.
We note that \(\mathsf {A_3} = \mathsf {PK}||\mathsf {M}\), and by \(\mathsf {A_3}/\mathsf {PK}\), we mean removing \(\mathsf {PK}\) from \(\mathsf {A_3}\).
References
Andreeva, E., Bogdanov, A., Dodis, Y., Mennink, B., Steinberger, J.P.: On the indifferentiability of key-alternating ciphers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 531–550. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_29
Barbosa, M., Farshim, P.: Indifferentiable authenticated encryption. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10991, pp. 187–220. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_7
Bellare, M., Boldyreva, A., O’Neill, A.: Deterministic and efficiently searchable encryption. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 535–552. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_30
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Proceedings of the 1st ACM Conference on Computer and Communications Security, pp. 62–73. ACM (1993)
Black, J.: The ideal-cipher model, revisited: an uninstantiable blockcipher-based hash function. In: Robshaw, M. (ed.) FSE 2006. LNCS, vol. 4047, pp. 328–340. Springer, Heidelberg (2006). https://doi.org/10.1007/11799313_21
Bleichenbacher, D.: Chosen ciphertext attacks against protocols based on the RSA encryption standard PKCS #1. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 1–12. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055716
Canetti, R., Goldreich, O., Halevi, S.: The random oracle methodology, revisited. J. ACM 51(4), 557–594 (2004)
Coron, J.-S., Dodis, Y., Malinaud, C., Puniya, P.: Merkle-Damgård revisited: how to construct a hash function. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 430–448. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_26
Coron, J.-S., Dodis, Y., Mandal, A., Seurin, Y.: A domain extender for the ideal cipher. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 273–289. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_17
Coron, J.-S., Holenstein, T., Künzler, R., Patarin, J., Seurin, Y., Tessaro, S.: How to build an ideal cipher: the indifferentiability of the Feistel construction. J. Cryptol. 29(1), 61–114 (2016). https://doi.org/10.1007/s00145-014-9189-6
Diffie, W., Hellman, M.: New directions in cryptography. IEEE Trans. Inf. Theory 22(6), 644–654 (1976)
Dodis, Y., Ristenpart, T., Shrimpton, T.: Salvaging Merkle-Damgård for practical applications. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 371–388. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_22
Dodis, Y., Stam, M., Steinberger, J., Liu, T.: Indifferentiability of confusion-diffusion networks. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 679–704. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_24
Freire, E.S.V., Hofheinz, D., Kiltz, E., Paterson, K.G.: Non-interactive key exchange. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 254–271. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_17
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. J. Cryptol. 26(1), 80–101 (2011). https://doi.org/10.1007/s00145-011-9114-1
Galbraith, S.D., Petit, C., Shani, B., Ti, Y.B.: On the security of supersingular isogeny cryptosystems. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 63–91. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_3
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 8–26. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_2
Jao, D., De Feo, L.: Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. In: Yang, B.-Y. (ed.) PQCrypto 2011. LNCS, vol. 7071, pp. 19–34. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25405-5_2
Jost, D., Maurer, U.: Security definitions for hash functions: combining UCE and indifferentiability. In: Catalano, D., De Prisco, R. (eds.) SCN 2018. LNCS, vol. 11035, pp. 83–101. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98113-0_5
Maurer, U., Renner, R., Holenstein, C.: Indifferentiability, impossibility results on reductions, and applications to the random oracle methodology. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 21–39. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_2
Mittelbach, A.: Salvaging indifferentiability in a multi-stage setting. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 603–621. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_33
Ristenpart, T., Shacham, H., Shrimpton, T.: Careful with composition: limitations of the indifferentiability framework. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 487–506. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_27
Rivest, R.L., Shamir, A., Adleman, L.: A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21(2), 120–126 (1978)
Rogaway, P., Shrimpton, T.: A provable-security treatment of the key-wrap problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 373–390. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_23
Shannon, C.E.: Communication theory of secrecy systems. Bell Syst. Tech. J. 28(4), 656–715 (1949)
Shoup, V.: Lower bounds for discrete logarithms and related problems. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 256–266. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_18
Zhandry, M., Zhang, C.: Indifferentiability for public key cryptosystems. Cryptology ePrint Archive, Report 2019/370 (2019). https://eprint.iacr.org/2019/370
Zhu, B., Li, K., Patterson, H.: Avoiding the disk bottleneck in the data domain deduplication file system. In: Proceedings of the 6th USENIX Conference on File and Storage Technologies, FAST 2008, pp. 18:1–18:14. USENIX Association, Berkeley (2008)
Acknowledgments
We thank Prof. Martin Albrecht for navigating the revisions of our paper as a shepherd. We thank the anonymous reviewers of Eurocrypt’2020 for pointing out a proof flaw in our earlier version. Mark Zhandry is supported by the Defense Advanced Research Projects Agency through the ARL under Contract W911NF-15-C-0205 and NSF grant 1616442. The views expressed are those of the authors and do not reflect the official policy or position of the Department of Defense or the National Science Foundation.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Zhandry, M., Zhang, C. (2020). Indifferentiability for Public Key Cryptosystems. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12170. Springer, Cham. https://doi.org/10.1007/978-3-030-56784-2_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-56784-2_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56783-5
Online ISBN: 978-3-030-56784-2
eBook Packages: Computer ScienceComputer Science (R0)








 ;
;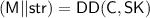 , it outputs
, it outputs