Abstract
We give a framework for relating the concrete security of a “reference” protocol (say, one appearing in an academic paper) to that of some derived, “real” protocol (say, appearing in a cryptographic standard). It is based on the indifferentiability framework of Maurer, Renner, and Holenstein (MRH), whose application has been exclusively focused upon non-interactive cryptographic primitives, e.g., hash functions and Feistel networks. Our extension of MRH is supported by a clearly defined execution model and two composition lemmata, all formalized in a modern pseudocode language. Together, these allow for precise statements about game-based security properties of cryptographic objects (interactive or not) at various levels of abstraction. As a real-world application, we design and prove tight security bounds for a potential TLS 1.3 extension that integrates the SPAKE2 password-authenticated key-exchange into the handshake.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The recent effort to standardize TLS 1.3 [44] was remarkable in that it leveraged provable security results as part of the drafting process [40]. Perhaps the most influential of these works is Krawczyk and Wee’s OPTLS authenticated key-exchange (AKE) protocol [35], which served as the basis for an early draft of the TLS 1.3 handshake. Core features of OPTLS are recognizable in the final standard, but TLS 1.3 is decidedly not OPTLS. As is typical of the standardization process, protocol details were modified in order to address deployment and operational desiderata (cf. [40, §4.1]). Naturally, this raises the question of what, if any, of the proven security that supported the original AKE protocol is inherited by the standard. The objective of this paper is to answer a general version of this question, quantitatively:
Given a reference protocol \(\tilde{\varPi }\) (e.g., OPTLS), what is the cost, in terms of concrete security [7], of translating \(\tilde{\varPi }\) into some real protocol \(\varPi \) (e.g., TLS 1.3) with respect to the security notion(s) targeted by \(\tilde{\varPi }\)?
Such a quantitative assessment is particularly useful for standardization because real-world protocols tend to provide relatively few choices of security parameters; and once deployed, the chosen parameters are likely to be in use for several years [33].
A more recent standardization effort provides an illustrative case study. At the time of writing, the CFRGFootnote 1 was in the midst of selecting a portfolio of password-authenticated key-exchange (PAKE) protocols [10] to recommend to the IETFFootnote 2 for standardization. Among the selection criteria [51] is the suitability of the PAKE for integration into existing protocols. In the case of TLS, the goal would be to standardize an extension (cf. [44, §4.2]) that specifies the usage of the PAKE in the handshake, thereby enabling defense-in-depth for applications in which (1) passwords are available for use in authentication, and (2) sole reliance on the web PKI for authentication is undesirable, or impossible. Tight security bounds are particularly important for PAKEs, since their security depends so crucially on the password’s entropy. Thus, the PAKE’s usage in TLS (i.e., the real protocol \(\varPi \)) should preserve the concrete security of the PAKE itself (i.e., the reference protocol \(\tilde{\varPi }\)), insofar as possible.
The direct route to quantifying this gap is to re-prove security of the derived protocol \(\varPi \) and compare the new bound to the existing one. This approach is costly, however: particularly when the changes from \(\tilde{\varPi }\) to \(\varPi \) seem insignificant, generating a fresh proof is likely to be highly redundant. In such cases it is common to instead provide an informal security argument that sketches the parts of the proof that would need to be changed, as well as how the security bound might be affected (cf. [35, §5]). Yet whether or not this approach is reasonable may be hard to intuit. Our experience suggests that it is often difficult to estimate the significance of a change before diving into the proof.
Another difficulty with the direct route is that the reference protocol’s concrete security might not be known, at least with respect to a specific attack model and adversarial goal. Simulation-style definitions, such as those formalized in the UC framework [20], define security via the inability of an environment (universally quantified, in the case of UC) to distinguish between attacks against the real protocol and attacks against an ideal protocol functionality. While useful in its own right, a proof of security relative to such a definition does not immediately yield concrete security bounds for a particular attack model or adversarial goal.
This work articulates an alternative route in which one argues security of \(\varPi \) by reasoning about the translation of \(\tilde{\varPi }\) into \(\varPi \) itself. Its translation framework (described in §2 and introduced below) provides a formal characterization of translations that are “safe”, in the sense that they allow security for \(\varPi \) to be argued by appealing to what is already known (or assumed) to hold for \(\tilde{\varPi }\). The framework is very general, and so we expect it to be broadly useful. In this work we will demonstrate its utility for standards development by applying it to the design and analysis of a TLS extension for SPAKE2 [3], one of the PAKEs considered by the CFRG for standardization. Our result (Theorem 1) precisely quantifies the security loss incurred by this usage of SPAKE2, and does so in a way that directly lifts existing results for SPAKE2 [1, 3, 6] while being largely agnostic about the targeted security notions.
The full version [42]. This article is the extended abstract of our paper. The full version includes all deferred proofs, as well as additional results, remarks, and discussion.
Overview. Our framework begins with a new look at an old idea. In particular, we extend the notion of indifferentiability of Maurer, Renner, and Holenstein [38] (hereafter MRH) to the study of cryptographic protocols.
Indifferentiability has become an important tool for provable security. Most famously, it provides a precise way to argue that the security in the random oracle model (ROM) [12] is preserved when the random oracle (RO) is instantiated by a concrete hash function that uses a “smaller” idealized primitive, such as a compression function modeled as an RO. Coron et al. [26] were the first to explore this application of indifferentiability, and due to the existing plethora of ROM-based results and the community’s burgeoning focus on designing replacements for SHA-1 [53], the use of indifferentiability in the design and analysis of hash functions has become commonplace.
Despite this focus, the MRH framework is more broadly applicable. A few works have leveraged this, e.g.: to construct ideal ciphers from Feistel networks [27]; to define security of key-derivation functions in the multi-instance setting [11]; to unify various security goals for authenticated encryption [4]; or to formalize the goal of domain separation in the ROM [8]. Yet all of these applications of indifferentiability are about cryptographic primitives (i.e., objects that are non-interactive). To the best of our knowledge, ours is the first work to explicitly consider the application of indifferentiability to protocols. That said, we will show that our framework unifies the formal approaches underlying a variety of prior works [17, 31, 41].
Our conceptual starting point is a bit more general than MRH. In particular, we define indifferentiability in terms of the world in which the adversary finds itself, so named because of the common use of phrases like “real world”, “ideal world”, and “oracle worlds” when discussing security definitions. Formally, a world is a particular kind of object (defined in §2.1) that is constructed by connecting up a game [15] with a scheme, the former defining the security goal of the latter. The scheme is embedded within a system that specifies how the adversary and game interact with it, i.e., the scheme’s execution environment.
Intuitively, when a world and an adversary are executed together, we can measure the probability of specific events occurring as a way to define adversarial success. Our  security experiment, illustrated in the left panel of Fig. 1, captures this. The outcome of the experiment is 1 (“true”) if the adversary A “wins”, as determined by the output w of world W, and predicate \(\psi \) on the transcript \( tx \) of the adversary’s queries also evaluates to 1. Along the lines of “penalty-style” definitions
[47], the transcript predicate determines whether or not A’s attack was valid, i.e., whether the attack constitutes a trivial win. (For example, if W captures IND-CCA security of an encryption scheme, then \(\psi \) would penalize decryption of challenge ciphertexts.)
security experiment, illustrated in the left panel of Fig. 1, captures this. The outcome of the experiment is 1 (“true”) if the adversary A “wins”, as determined by the output w of world W, and predicate \(\psi \) on the transcript \( tx \) of the adversary’s queries also evaluates to 1. Along the lines of “penalty-style” definitions
[47], the transcript predicate determines whether or not A’s attack was valid, i.e., whether the attack constitutes a trivial win. (For example, if W captures IND-CCA security of an encryption scheme, then \(\psi \) would penalize decryption of challenge ciphertexts.)
Shared-Resource Indifferentiability and The Lifting Lemma. Also present in the experiment is a (possibly empty) tuple of resources \(\vec {R}\), which may be called by both the world W and the adversary A. This captures embellishments to the base security experiment that may be used to prove security, but are not essential to the definition of security itself. An element of \(\vec {R}\) might be an idealized object such as an RO [12], ideal cipher [27], or generic group [43]; it might be used to model global trusted setup, such as distribution of a common reference string [22]; or it might provide A (and W) with an oracle that solves some hard problem, such as the DDH oracle in the formulation of the Gap DH problem [39].
The result is a generalized notion of indifferentiability that we call shared-resource indifferentiability. The  experiment, illustrated in the right panel of Fig. 1, considers an adversary’s ability to distinguish some real world/resource pair \(W/\vec {R}\) (read “W with \(\vec {R}\)”) from a reference world/resource pair \(V/\vec {Q}\) when the world and the adversary share access to the resources. The real world W exposes two interfaces to the adversary, denoted by subscripts \(W_1\) and \(W_2\), that we will call the main and auxiliary interfaces of W, respectively. The reference world V also exposes two interfaces (with the same monikers), although the adversary’s access to the auxiliary interface of V is mediated by a simulator S. Likewise, the adversary has direct access to resources \(\vec {R}\) in the real experiment, and S-mediated access to resources \(\vec {Q}\) in the reference experiment.
experiment, illustrated in the right panel of Fig. 1, considers an adversary’s ability to distinguish some real world/resource pair \(W/\vec {R}\) (read “W with \(\vec {R}\)”) from a reference world/resource pair \(V/\vec {Q}\) when the world and the adversary share access to the resources. The real world W exposes two interfaces to the adversary, denoted by subscripts \(W_1\) and \(W_2\), that we will call the main and auxiliary interfaces of W, respectively. The reference world V also exposes two interfaces (with the same monikers), although the adversary’s access to the auxiliary interface of V is mediated by a simulator S. Likewise, the adversary has direct access to resources \(\vec {R}\) in the real experiment, and S-mediated access to resources \(\vec {Q}\) in the reference experiment.
The auxiliary interface captures what changes as a result of translating world \(V/\vec {Q}\) into \(W/\vec {R}\): the job of the simulator S is to “fool” the adversary into believing it is interacting with \(W/\vec {R}\) when in fact it is interacting with \(V/\vec {Q}\). Intuitively, if for a given adversary A there is a simulator S that successfully “fools” it, then this should yield a way to translate A’s attack against \(W/\vec {R}\) into an attack against \(V/\vec {Q}\). This intuition is captured by our “lifting” lemma (Lemma 1, §2.3), which says that if \(V/\vec {Q}\) is  -secure and \(W/\vec {R}\) is indifferentiable from \(V/\vec {Q}\) (as captured by
-secure and \(W/\vec {R}\) is indifferentiable from \(V/\vec {Q}\) (as captured by  ), then \(W/\vec {R}\) is also
), then \(W/\vec {R}\) is also  -secure.
-secure.
Games and The Preservation Lemma. For all applications in this paper, a world is specified in terms of two objects: the intended security goal of a scheme, formalized as a (single-stage [45]) game; and the system that specifies the execution environment for the scheme. In §2.4 we specify a world \(W=\mathbf{Wo} (G, X)\) whose main interface allows the adversary to “play” the game G and whose auxiliary interface allows it to interact with the system X.
The world’s auxiliary interface captures what “changes” from the reference experiment to the real one, and the main interface captures what stays the same. Intuitively, if a system X is indifferentiable from Y, then it ought to be the case that world \(\mathbf{Wo} (G, X)\) is indifferentiable from \(\mathbf{Wo} (G, Y)\), since in the former setting, the adversary might simply play the game G in its head. Thus, by Lemma 1, if Y is secure in the sense of G, then so is X. We formalize this intuition via a simple “preservation” lemma (Lemma 2, §2.4), which states that the indifferentiability of X from Y is “preserved” when access to X’s (resp. Y’s) main interface is mediated by a game G. As we show in §2.4, this yields the main result of MRH as a corollary (cf. [38, Theorem 1]).
Updated Pseudocode. An important feature of our framework is its highly expressive pseudocode. MRH define indifferentiability in terms of “interacting systems” formalized as sequences of conditional probability distributions (cf. [38, §3.1]). This abstraction, while extremely expressive, is much harder to work with than conventional cryptographic pseudocode. A contribution of this paper is to articulate an abstraction that provides much of the expressiveness of MRH, while preserving the level of rigor typical of game-playing proofs of security [15]. In §2.1 we formalize objects, which are used to define the various entities that run in security experiments, including games, adversaries, systems, and schemes.
Execution Environment for eCK-Protocols. Finally, in order define indifferentiability for cryptographic protocols we need to precisely specify the system X (i.e., execution environment) in which the protocol runs. In §3.1 we specify the system \(X=\mathbf{eCK} (\varPi )\) that captures the interaction of the adversary with protocol \(\varPi \) in the extended Canetti-Krawczyk (eCK) model [37]. The auxiliary interface of X is used by the adversary to initiate and execute sessions of \(\varPi \) and corrupt parties’ long-term and per-session secrets. The main interface of X is used by the game in order to determine if the adversary successfully “attacked” \(\varPi \).
Note that our treatment breaks with the usual abstraction boundary. In its original presentation [37], the eCK model encompasses both the execution environment and the intended security goal; but in our setting, the full model is obtained by specifying a game G that codifies the security goal and running the adversary in world \(W=\mathbf{Wo} (G,\mathbf{eCK} (\varPi ))\). As we discuss in §3.1, this allows us to use indifferentiability to prove a wide range of security goals without needing to attend to the particulars of each goal.
Case Study: Design of a PAKE Extension for TLS. Our framework lets us make precise statements of the following form: “protocol \(\varPi \) is \(G^{}\)-secure if protocol \(\tilde{\varPi }\) is \(G^{}\)-secure and the execution of \(\varPi \) is indifferentiable from the execution of \(\tilde{\varPi }\).” This allows us to argue that \(\varPi \) is secure by focusing on what changes from \(\tilde{\varPi }\) to \(\varPi \). In §3.2 we provide a demonstration of this methodology in which we design and derive tight security bounds for a TLS extension that integrates SPAKE2 [3] into the handshake. Our proposal is based on existing Internet-Drafts [5, 36] and discussions on the CFRG mailing list [18, 55].
Our analysis (Theorem 1) unearths some interesting and subtle design issues. First, existing PAKE-extension proposals [5, 54] effectively replace the DH key-exchange with execution of the PAKE, feeding the PAKE’s output into the key schedule instead of the usual shared secret. As we will discuss, whether this usage of the output is “safe” depends on the particular PAKE and its security properties. Second, our extension adopts a “fail closed” posture, meaning if negotiation of the PAKE fails, then the client and server tear down the session. Existing proposals allow them to “fail open” by falling back to standard, certificate-only authentication. There is no way to account for this behavior in the proof of Theorem 1, at least not without relying on the security of the standard authentication mechanism. But this in itself is interesting, as it reflects the practical motivation for integrating a PAKE into TLS: it makes little sense to fail open if one’s goal is to reduce reliance on the web PKI.
Partially Specified Protocols. TLS specifies a complex protocol, and most of the details are irrelevant to what we want to prove. The Partially Specified Protocol (PSP) framework of Rogaway and Stegers [46] offers an elegant way to account for these details without needing to specify them exhaustively. Their strategy is to divide a protocol’s specification into two components: the protocol core (PC), which formalizes the elements of the protocol that are essential to the security goal; and the specification details (SD), which captures everything else. The PC, fully specified in pseudocode, is defined in terms of calls to an SD oracle. Security experiments execute the PC, but it is the adversary who is responsible for answering SD-oracle queries. This formalizes a very strong attack model, but one that yields a rigorous treatment of the standard itself, rather than a boiled down version of it.
We incorporate the PSP framework into our setting by allowing the world to make calls to the adversary’s auxiliary interface, as shown in Fig. 1. In addition, the execution environment \(\mathbf{eCK} \) and world-builder \(\mathbf{Wo} \) are specified so that the protocol’s SD-oracle queries are answered by the adversary.
Related Work. Our formal methodology was inspired by a few seemingly disparate results in the literature, but which fit fairly neatly into the translation framework. Recent work by the authors
[41] considers the problem of secure key-reuse
[31], where the goal is design cryptosystems that safely expose keys for use in multiple applications. They formalize a condition (GAP1, cf.
[41, Def. 5]) under which the G-security of a system X implies that G-security of X holds even when X’s interface is exposed to additional, insecure, or even malicious applications. This condition can be formulated as a special case of  security, and their composition theorem (cf.
[41, Theorem 1]) as a corollary of our lifting lemma. The lifting lemma can also be thought of as a computational analogue of the main technical tool in Bhargavan et al. ’s treatment of downgrade resilience (cf.
[17, Theorem 2]). We discuss this connection in detail in the full version.
security, and their composition theorem (cf.
[41, Theorem 1]) as a corollary of our lifting lemma. The lifting lemma can also be thought of as a computational analogue of the main technical tool in Bhargavan et al. ’s treatment of downgrade resilience (cf.
[17, Theorem 2]). We discuss this connection in detail in the full version.
The UC Framework. MRH point out (cf. [38, §3.3]) that the notion of indifferentiability is inspired by ideas introduced by the UC framework [20]. There are conceptual similarities between UC (in particular, the generalized UC framework that allows for shared state [21]) and our framework, but the two are quite different in their details. We do not explore any formal relationship between frameworks, nor do we consider how one might modify UC to account for things that are naturally handled by ours (e.g., translation and partially specified behavior [46]). Such an exploration would make interesting future work.
Provable Security of SPAKE2. The SPAKE2 protocol was first proposed and analyzed in 2005 by Abdalla and Pointcheval [3], who sought a simpler alternative to the seminal encrypted key-exchange (EKE) protocol of Bellovin and Merritt [16]. Given the CFRG’s recent interest in SPAKE2 (and its relative SPAKE2+ [25]), there has been a respectable amount of recent security analysis. This includes concurrent works by Abdalla and Barbosa [1] and Becerra et al. [6] that consider the forward secrecy of (variants of) SPAKE2, a property that Abdalla and Pointcheval did not address. Victor Shoup [49] provides an analysis of a variant of SPAKE2 in the UC framework [20], which has emerged as the de facto setting for studying PAKE protocols (cf. OPAQUE [32] and (Au)CPace [30]). Shoup observes that the usual notion of UC-secure PAKE [23] cannot be proven for SPAKE2, since the protocol on its own does not provide key confirmation. Indeed, many variants of SPAKE2 that appear in the literature add key confirmation in order to prove it secure in a stronger adversarial model (cf. [6, §3]).
A recent work by Skrobot and Lancrenon [50] characterizes the general conditions under which it is secure to compose a PAKE protocol with an arbitrary symmetric key protocol (SKP). While their object of study is similar to ours—a PAKE extension for TLS might be viewed as a combination of a PAKE and the TLS record layer protocol—our security goals are different, since in their adversarial model the adversary’s goal is to break the security of the SKP.
2 The Translation Framework
This section describes the formal foundation of this paper. We begin in §2.1 by defining objects, our abstraction of the various entities run in a security experiment; in §2.2 we define our base experiment and formalize shared-resource indifferentiability; in §2.3 we state the lifting lemma, the central technical tool of this work (we defer a proof to the full version); and in §2.4 we formalize the class of security goals to which our framework applies.
Notation. When X is a random variable we let \(\Pr \big [\,X=v\,\big ]\) denote the probability that X is equal to v; we write \(\Pr \big [\,X\,\big ]\) as shorthand for \(\Pr \big [\,X=1\,\big ]\). We let \(x\leftarrow y\) denote assignment of the value of y to variable x. When \(\mathcal {X}\) is a finite set we let  denote random assignment of an element of \(\mathcal {X}\) to x according to the uniform distribution.
denote random assignment of an element of \(\mathcal {X}\) to x according to the uniform distribution.
A string is an element of \(\{0,1\}^*\); a tuple is a finite sequence of symbols separated by commas and delimited by parentheses. Let \(\varepsilon \) denote the empty string, \((\,)\) the empty tuple, and (z, ) the singleton tuple containing z. We sometimes (but not always) denote a tuple with an arrow above the variable (e.g., \(\vec {x}\) ). Let |x| denote the length of a string (resp. tuple) x. Let \(x_i\) and x[i] denote the i-th element of x. Let \(x \, \Vert \,y\) denote concatenation of x with string (resp. tuple) y. We write \(x \preceq y\) if string x is a prefix of string y, i.e., there exists some r such that \(x\, \Vert \,r = y\). Let \(y \;\%\;x\) denote the “remainder” r after removing the prefix x from y; if \(x \not \preceq y\), then define \(y \;\%\;x=\varepsilon \) (cf. [19]). When x is a tuple we let \(x \,.\,z = (x_1, \ldots , x_{|x|}, z)\) so that z is “appended” to x. We write \(z \in x\) if \((\exists \,i)\,x_i=z\). Let [i..j] denote the set of integers \(\{i, \ldots , j\}\); if \(j < i\), then define [i..j] as \(\emptyset \). Let \([n] = [1..n]\).
For all sets \(\mathcal {X}\) and functions \(f, g : \mathcal {X}\rightarrow \{0,1\}\), define function \(f \wedge g\) as the map \([f \wedge g](x) \mapsto f(x)\wedge g(x)\) for all \(x\in \mathcal {X}\). We denote a group as a pair \((\mathcal {G},*)\), where \(\mathcal {G}\) is the set of group elements and \(*\) denotes the group action. Logarithms are base-2 unless otherwise specified.
2.1 Objects
Our goal is to preserve the expressiveness of the MRH framework [38] while providing the level of rigor of code-based game-playing arguments [15]. To strike this balance, we will need to add a bit of machinery to standard cryptographic pseudocode. Objects provide this.
Each object has a specification that defines how it is used and how it interacts with other objects. We first define specifications, then describe how to call an object in an experiment and how to instantiate an object. Pseudocode in this paper will be typed (along the lines of Rogaway and Stegers [46]), so we enumerate the available types in this section. We finish by defining various properties of objects that will be used in the remainder.
Specifications. The relationship between a specification and an object is analogous to (but far simpler than) the relationship between a class and a class instance in object-oriented programming languages like Python or
 . A specification defines an ordered sequence of variables stored by an object—these are akin to attributes in Python—and an ordered sequence of operators that may be called by other objects—these are akin to methods. We refer to the sequence of variables as the object’s state and to the sequence of operators as the object’s interface.
. A specification defines an ordered sequence of variables stored by an object—these are akin to attributes in Python—and an ordered sequence of operators that may be called by other objects—these are akin to methods. We refer to the sequence of variables as the object’s state and to the sequence of operators as the object’s interface.
Specification of a random oracle (RO) object. When instantiated, variables \(\mathcal {X}\) and \(\mathcal {Y}\) determine the domain and range of the RO, and integers q and p determine, respectively, the maximum number of distinct RO queries, and the maximum number of RO-programming queries (via the
 ), (cf. Definition 6).
), (cf. Definition 6).
We provide an example of a specification in Fig. 2. (We give a detailed description of the syntax in the full version.) Spec \(\mathbf{Ro} \) is used throughout this work to model functions as random oracles (ROs)
[12]. It declares seven variables, \(\mathcal {X}\), \(\mathcal {Y}\), q, p, T, i, and j, as shown on lines 1–2 in Fig. 2. (We will use shorthand for line references in the remainder, e.g., “2:1–2” rather than “lines 1–2 in Fig. 2”.) Each variable has an associated type: \(\mathcal {X}\) and \(\mathcal {Y}\) have type \(\mathbf{set} \), q, p, i, and j have type \(\mathbf{int} \), and T has type \(\mathbf{table} \). Variable declarations are denoted by the keyword “var”, while operator definitions are denoted by the keyword “
 ”. Spec \(\mathbf{Ro} \) defines three operators: the first, the
”. Spec \(\mathbf{Ro} \) defines three operators: the first, the
 -operator (2:3), initializes the RO’s state; the second operator (2:4–8) responds to standard RO queries; and the third, the
-operator (2:3), initializes the RO’s state; the second operator (2:4–8) responds to standard RO queries; and the third, the
 -operator (2:9–14), is used to “program” the RO
[29].
-operator (2:9–14), is used to “program” the RO
[29].
Calling an Object. An object is called by providing it with oracles and passing arguments to it. An oracle is always an interface, i.e., a sequence of operators defined by an object. The statement “\( out \leftarrow obj ^{\,\mathbf{I} _1,\ldots ,\mathbf{I} _m}( in _1, \ldots , in _n)\)” means to invoke one of \( obj \)’s operators on input of \( in _1, \ldots , in _n\) and with oracle access to interfaces \(\mathbf{I} _1,\ldots ,\mathbf{I} _m\) and set variable \( out \) to the value returned by the operator. Objects will usually have many operators, so we must specify the manner in which the responding operator is chosen. For this purpose we will adopt a convention inspired by “pattern matching” in functional languages like Haskell and Rust. A pattern is comprised of a tuple of literals, typed variables, and nested tuples. A value is said to match a pattern if they have the same type and the literals are equal. For example, value \( val \) matches pattern \((\,\underline{}\;\mathbf{elem} _{\mathcal {X}})\) if \( val \) has type \(\mathbf{elem} _{\mathcal {X}}\). (The symbol “\(\,\underline{}\)” contained in the pattern denotes an anonymous variable.) Hence, if object R is specified by \(\mathbf{Ro} \) and x has type \(\mathbf{elem} _{\mathcal {X}}\), then the expression “R(x)” calls R’s second operator (2:4–8). We write “\( val \sim pat \)” if the value of variable \( val \) matches pattern \( pat \).
Calls to objects are evaluated as follows. In the order in which they are defined, check each operator of the object’s specification if the input matches the operator’s pattern. If so, then execute the operator until a return statement is reached and assign the return value to the output. If no return statement is reached, or if \( val \) does not match an operator, then return \(\bot \).
Let us consider an illustrative example. Let \(\varPi \) be an object that implements Schnorr’s signature scheme
[48] for a group \((\mathcal {G}, \cdot )\) as specified in Figure 3. The expression
 calls \(\varPi \)’s first operator, which generates a fresh key pair. If \(s\in \mathbb {Z}\) and \( msg \in \{0,1\}^*\), then expression
calls \(\varPi \)’s first operator, which generates a fresh key pair. If \(s\in \mathbb {Z}\) and \( msg \in \{0,1\}^*\), then expression
 evaluates the third operator, which computes a signature (x, t) of message \( msg \) under secret key s (we will often write the first argument as a subscript). The call to interface oracle \(\mathcal {H}\) on line 3:5 is answered by object H. (Presumably, H is a hash function with domain \(\mathcal {G} \times \{0,1\}^*\) and range \(\mathbb {Z}_{|\mathcal {G}|}\).) If \( P\!K \in \mathcal {G}\), \( msg \in \{0,1\}^*\), and \(x,t\in \mathbb {Z}\), then expression
evaluates the third operator, which computes a signature (x, t) of message \( msg \) under secret key s (we will often write the first argument as a subscript). The call to interface oracle \(\mathcal {H}\) on line 3:5 is answered by object H. (Presumably, H is a hash function with domain \(\mathcal {G} \times \{0,1\}^*\) and range \(\mathbb {Z}_{|\mathcal {G}|}\).) If \( P\!K \in \mathcal {G}\), \( msg \in \{0,1\}^*\), and \(x,t\in \mathbb {Z}\), then expression
 evaluates the second operator. On an input that does not match any of these patterns—in particular, one of
evaluates the second operator. On an input that does not match any of these patterns—in particular, one of
 ,
,
 , or
, or
 —the object returns \(\bot \). For example,
—the object returns \(\bot \). For example,
 for any \(\mathbf{I} _1, \ldots , \mathbf{I} _m\).
for any \(\mathbf{I} _1, \ldots , \mathbf{I} _m\).
It is up to the caller to ensure that the correct number of interfaces is passed to the operator. If the number of interfaces passed is less than the number of oracles named by the operator, then calls to the remaining oracles are always answered with \(\bot \); if the number of interfaces is more than the number of oracles named by the operator, then the remaining interfaces are simply ignored by the operator.
Explanation. We will see examples of pattern matching in action throughout this paper. For now, the important takeaway is that calling an object results in one (or none) of its operators being invoked: which one is invoked depends on the type of input and the order in which the operators are defined.
Because these calling conventions are more sophisticated than usual, let us take a moment to explain their purpose. Theorem statements in this work will often quantify over large sets of objects whose functionality is unspecified. These conventions ensure that doing so is always well-defined, since any object can be called on any input, regardless of the input type. We could have dealt with this differently: for example, in their adaptation of indifferentiability to multi-staged games, Ristenpart et al. require a similar convention for functionalities and games (cf. “unspecified procedure” in [45, §2]). Our hope is that the higher level of rigor of our formalism will ease the task of verifying proofs of security in our framework.
Instantiating an Object. An object is instantiated by passing arguments to its specification. The statement “\( obj \leftarrow \mathbf{Object} ( in _1, \ldots , in _m)\)” means to create a new object \( obj \) of type \(\mathbf{Object} \) and initialize its state by setting \( obj . var _1 \leftarrow in _1\), ..., \( obj . var _m \leftarrow in _m\), where \( var _1, \ldots , var _m\) are the first m variables declared by \(\mathbf{Object} \). If the number of arguments passed is less than the number of variables declared, then the remaining variables are uninitialized. For example, the statement “\(R \leftarrow \mathbf{Ro} (\mathcal {X},\mathcal {Y}, q, p, [\,], 0, 0)\)” initializes R by setting \(R.\mathcal {X}\leftarrow \mathcal {X}\), \(R.\mathcal {Y}\leftarrow \mathcal {Y}\), \(R.q\leftarrow q\), \(R.p \leftarrow p\), \(R.T \leftarrow [\,]\), \(R.i \leftarrow 0\), and \(R.j \leftarrow 0\). The statement “\(R \leftarrow \mathbf{Ro} (\mathcal {X}, \mathcal {Y}, q, p)\)” sets \(R.\mathcal {X}\leftarrow \mathcal {X}\), \(\mathcal {R}.\mathcal {Y}\leftarrow \mathcal {Y}\), \(R.q\leftarrow q\), and \(R.p \leftarrow p\), but leaves T, i, and j uninitialized. Object can also be copied: the statement “\( new \leftarrow obj \)” means to instantiate a new object \( new \) with specification \(\mathbf{Object} \) and set \( new . var _1 \leftarrow obj . var _1, \ldots , new . var _n \leftarrow obj . var _n\), where \( var _1, \ldots , var _n\) is the sequence of variables declared by \( obj \)’s specification.
Types. We now enumerate the types available in our pseudocode. An object has type \(\mathbf{object} \). A set of values of type \(\mathbf{any} \) (defined below) has type \(\mathbf{set} \); we let \(\emptyset \) denote the empty set. A variable of type \(\mathbf{table} \) stores a table of key/value pairs, where keys and values both have type \(\mathbf{any} \). If T is a table, then we let \(T_k\) and T[k] denote the value associated with key k in T; if no such value exists, then \(T_k =\bot \). We let \([\,]\) denote the empty table.
When the value of a variable x is an element of a computable set \(\mathcal {X}\), we say that x has type \(\mathbf{elem} _{\mathcal {X}}\). We define type \(\mathbf{int} \) as an alias of \(\mathbf{elem} _{\mathbb {Z}}\), type \(\mathbf{bool} \) as an alias of \(\mathbf{elem} _{\{0,1\}}\), and type \(\mathbf{str} \) as an alias of \(\mathbf{elem} _{\{0,1\}^*}\). We define type \(\mathbf{any} \) recursively as follows. A variable x is said to have type \(\mathbf{any} \) if: it is equal to \(\bot \) or \((\,)\); has type \(\mathbf{set} \), \(\mathbf{table} \), or \(\mathbf{elem} _{\mathcal {X}}\) for some computable set \(\mathcal {X}\); or it is a tuple of values of type \(\mathbf{any} \).
Specifications declare the type of each variable of an object’s state. The types of variables that are local to the scope of an operator need not be explicitly declared, but their type must be inferable from their initialization (that is, the first use of the variable in an assignment statement). If a variable is assigned a value of a type other than the variable’s type, then the variable is assigned \(\bot \). Variables that are declared but not yet initialized have the value \(\bot \). For all \(\mathbf{I} _1,\ldots ,\mathbf{I} _m, in _1, \ldots , in _n\) the expression “\(\bot ^\mathbf{I _1,\ldots ,\mathbf{I} _m}( in _1, \ldots , in _n)\)” evaluates to \(\bot \). We say that \(x = \bot \) or \(\bot = x\) if variable x was previously assigned \(\bot \). For all other expressions, our convention will be that whenever \(\bot \) is an input, the expression evaluates to \(\bot \).
Properties of Operators and Objects. An operator is called deterministic if its definition does not contain a random assignment statement; it is called stateless if its definition contains no assignment statement in which one of the object’s variables appears on the left-hand side; and an operator is called functional if it is deterministic and stateless. Likewise, an object is called deterministic (resp. stateless or functional) if each operator, with the exception of the
 , is deterministic (resp. stateless or functional). (We make an exception for the
, is deterministic (resp. stateless or functional). (We make an exception for the
 in order to allow trusted setup of objects executed in our experiments. See §2.2 for details.)
in order to allow trusted setup of objects executed in our experiments. See §2.2 for details.)
Resources. Let \(t\in \mathbb {N}\). An operator is called t-time if it always halts in t time steps regardless of its random choices or the responses to its queries; we say that an operator is halting if it is t-time for some \(t < \infty \). Our convention will be that an operator’s runtime includes the time required to evaluate its oracle queries. Let \(\vec {q}\in \mathbb {N}^*\). An operator is called \(\vec {q}\)-query if it makes at most \(\vec {q}_1\) calls to its first oracle, \(\vec {q}_2\) to its second, and so on. We extend these definitions to objects, and say that an object is t-time (resp. halting or \(\vec {q}\)-query) if each operator of its interface is t-time (resp. halting or \(\vec {q}\)-query).
Exported Operators. An operator \(f_1\) is said to shadow operator \(f_2\) if: (1) \(f_1\) appears first in the sequence of operators defined by the specification; and (2) there is some input that matches both \(f_1\) and \(f_2\). For example, an operator with pattern \((x\;\mathbf{any} )\) would shadow an operator with pattern \((y \;\mathbf{str} )\), since y is of type \(\mathbf{str} \) and \(\mathbf{any} \). An object is said to export a \( pat \)-\( type \)-operator if its specification defines a non-shadowed operator that, when run on an input matching pattern \( pat \), always returns a value of type \( type \).
2.2 Experiments and Indifferentiability
This section describes our core security experiments. An experiment connects up a set of objects in a particular way, giving each object oracle access to interfaces (i.e., sequences of operators) exported by other objects. An object’s i-interface is the sequence of operators whose patterns are prefixed by literal i. We sometimes write i as a subscript, e.g., “\(X_i(\,\cdots )\)” instead of “\(X(i, \cdots )\)” or “\(X(i, (\,\cdots ))\)”. We refer to an object’s 1-interface as its main interface and to its 2-interface as its auxiliary interface.
A resource is a halting object. A simulator is a halting object. An adversary is a halting object that exports a
 -operator, which means that on input of
-operator, which means that on input of
 to its main interface, it outputs a bit. This operator is used to in order to initiate the adversary’s attack. The attack is formalized by the adversary’s interaction with another object, called the world, which codifies the system under attack and the adversary’s goal. Formally, a world is a halting object that exports a functional
to its main interface, it outputs a bit. This operator is used to in order to initiate the adversary’s attack. The attack is formalized by the adversary’s interaction with another object, called the world, which codifies the system under attack and the adversary’s goal. Formally, a world is a halting object that exports a functional
 -\(\mathbf{bool} \)-operator, which means that on input of
-\(\mathbf{bool} \)-operator, which means that on input of
 to its main interface, the world outputs a bit that determines if the adversary has won. The operator being functional means this decision is made deterministically and in a “read-only” manner, so that the object’s state is not altered. (These features are necessary to prove the lifting lemma in §2.3.)
to its main interface, the world outputs a bit that determines if the adversary has won. The operator being functional means this decision is made deterministically and in a “read-only” manner, so that the object’s state is not altered. (These features are necessary to prove the lifting lemma in §2.3.)
MAIN Security. Security experiments are formalized by the execution of procedure \(\mathbf{Real} ^{{}}\) defined in Fig. 4 for adversary A in world W with shared resources \(\vec {R}=(R_1,\ldots ,R_u)\). In addition, the procedure is parameterized by a function \(\varPhi \). The experiment begins by “setting up” each object by running
 ,
,
 , and
, and
 for each \(i\in [u]\). This allows for trusted setup of each object before the attack begins. Next, the procedure runs A with oracle access to procedures \(\mathbf{W} _1\), \(\mathbf{W} _2\), and \(\mathbf{R} \), which provide A with access to, respectively, W’s main interface, W’s auxiliary interface, and the resources \(\vec {R}\).
for each \(i\in [u]\). This allows for trusted setup of each object before the attack begins. Next, the procedure runs A with oracle access to procedures \(\mathbf{W} _1\), \(\mathbf{W} _2\), and \(\mathbf{R} \), which provide A with access to, respectively, W’s main interface, W’s auxiliary interface, and the resources \(\vec {R}\).
Figure 1 illustrates which objects have access to which interfaces. The world W and adversary A share access to the resources \(\vec {R}\). In addition, the world has access to the auxiliary interface of A (4:5), which allows us to formalize security properties in the PSP setting
[46]. Each query to \(\mathbf{W} _1\) or \(\mathbf{W} _2\) by A is recorded in a tuple \( tx \) called the experiment transcript (4:5). The outcome of the experiment is \(\varPhi ( tx , a, w)\), where a is the bit output by A and w is the bit output by W. The  security notion, defined below, captures an adversary’s advantage in “winning” in a given world, where what it means to “win” is defined by the world itself. The validity of the attack is defined by a function \(\psi \), called the transcript predicate: in the
security notion, defined below, captures an adversary’s advantage in “winning” in a given world, where what it means to “win” is defined by the world itself. The validity of the attack is defined by a function \(\psi \), called the transcript predicate: in the  experiment, we define \(\varPhi \) so that \(\mathbf{Real} ^{{\varPhi }}_{W/\vec {R}}(A)=1\) holds if A wins and \(\psi ( tx )=1\) holds.
experiment, we define \(\varPhi \) so that \(\mathbf{Real} ^{{\varPhi }}_{W/\vec {R}}(A)=1\) holds if A wins and \(\psi ( tx )=1\) holds.
Definition 1
(\(\mathbf {MAIN}^{\psi }\) security). Let W be a world, \(\vec {R}\) be resources, and A be an adversary. Let \(\psi \) be a transcript predicate, and let \(\mathsf {win}^\psi ( tx ,a,w)\,:=\,(\psi ( tx )=1)\wedge (w\!=\!1)\). The \(\text {MAIN}^{\psi }\) advantage of A in attacking \(W/\vec {R}\) is

Informally, we say that \(W/\vec {R}\) is \(\psi \)-secure if the \(\text {MAIN}^{\psi }\) advantage of every efficient adversary is small. Note that advantage for indistinguishability-style security notions is defined by normalizing \(\text {MAIN}^{\psi }\) advantage (e.g., Definition 11 in the full version). \(\square \)
This measure of advantage is only meaningful if \(\psi \) is efficiently computable, since otherwise a computationally bounded adversary may lack the resources needed to determine if its attack is valid. Following Rogaway-Zhang (cf. computability of “fixedness” in [47, §2]) we will require \(\psi ( tx )\) to be efficiently computable given the entire transcript, except the response to the last query. Intuitively, this exception ensures that, at any given moment, the adversary “knows” whether its next query is valid before making it.
Definition 2
(Transcript-predicate computability). Let \(\psi \) be a transcript predicate. Object F computes \(\psi \) if it is halting, functional, and \(F(\bar{ tx })=\psi ( tx )\) holds for all transcripts \( tx \), where \(\bar{ tx } = ( tx _1, \ldots , tx _{q-1}, (i_q, x_q,\bot )) \,,\) \(q = | tx |\), and \((i_q, x_q, \,\underline{}\,) = tx _{q}\). We say that \(\psi \) is computable if there is an object that computes it. We say that \(\psi \) is t-time computable if there is a t-time object F that computes it. Informally, we say that \(\psi \) is efficiently computable if it is t-time computable for small t. \(\square \)
Shorthand. In the remainder we write “\(W/\vec {R}\)” as “\(W/H\)” when “\(\vec {R}=(H,)\)”, i.e., when the resource tuple is a singleton containing H. Similarly, we write “\(W/\vec {R}\)” as “W” when \(\vec {R}=(\,)\), i.e., when no shared resources are available. We write “\(\mathsf {win}\)” instead of “\(\mathsf {win}^\psi \)” whenever \(\psi \) is defined so that \(\psi ( tx )=1\) for all transcripts \( tx \). Correspondingly, we write “MAIN” for the security notion obtained by letting \(\varPhi =\mathsf {win}\).
SR-INDIFF Security. The \(\mathbf{Real} ^{{}}\) procedure executes an adversary in a world that shares resources with the adversary. We are interested in the adversary’s ability to distinguish this “real” experiment from a “reference” experiment in which we change the world and/or resources with which the adversary interacts. To that end, Fig. 4 also defines the \(\mathbf {Ref}\) procedure, which executes an adversary in a fashion similar to \(\mathbf{Real} ^{{}}\) except that a simulator S mediates the adversary’s access to the resources and the world’s auxiliary interface. In particular, A’s oracles \(\mathbf{W} _2\) and \(\mathbf{R} \) are replaced with \(\mathbf{S} _2\) and \(\mathbf{S} _3\) respectively (4:7 and 10), which run S with access to \(\mathbf{W} _2\) and \(\mathbf{R} \) (4:13).  advantage, defined below, measures the adversary’s ability to distinguish between a world \(W/\vec {R}\) in the real experiment and another world \(V/\vec {Q}\) in the reference experiment.
advantage, defined below, measures the adversary’s ability to distinguish between a world \(W/\vec {R}\) in the real experiment and another world \(V/\vec {Q}\) in the reference experiment.
Definition 3
(  security). Let W, V be worlds, \(\vec {R}, \vec {Q}\) be resources, A be an adversary, and S be a simulator. Let \(\psi \) be a transcript predicate and let \(\mathsf {out}^\psi ( tx ,a,w) \,:=\,(\psi ( tx )=1)\wedge (a\!=\!1)\). Define the
security). Let W, V be worlds, \(\vec {R}, \vec {Q}\) be resources, A be an adversary, and S be a simulator. Let \(\psi \) be a transcript predicate and let \(\mathsf {out}^\psi ( tx ,a,w) \,:=\,(\psi ( tx )=1)\wedge (a\!=\!1)\). Define the
 advantage of adversary A in differentiating \(W/\vec {R}\) from \(V/\vec {Q}\) relative to S as
advantage of adversary A in differentiating \(W/\vec {R}\) from \(V/\vec {Q}\) relative to S as

By convention, the runtime of A is the runtime of \(\mathbf{Real} ^{{\mathsf {out}^\psi }}_{W/\vec {R}}(A)\). Informally, we say that \(W/\vec {R}\) is \(\psi \)-indifferentiable from \(V/\vec {Q}\) if for every efficient A there exists an efficient S for which the  advantage of A is small. \(\square \)
advantage of A is small. \(\square \)
Shorthand. We write “\(\mathsf {out}\)” instead of “\(\mathsf {out}^\psi \)” when \(\psi \) is defined so that \(\psi ( tx )=1\) for all \( tx \). Correspondingly, we write “SR-INDIFF” for the security notion obtained by letting \(\varPhi =\mathsf {out}\).
Non-Degenerate Adversaries. When defining security, it is typical to design the experiment so that it is guaranteed to halt. Indeed, there are pathological conditions under which \(\mathbf{Real} ^{{\varPhi }}_{W/\vec {R}}(A)\) and \(\mathbf{Ref} ^{{\varPhi }}_{W/\vec {R}}(A, S)\) do not halt, even if each of the constituent objects is halting (as defined in §2.1). This is because infinite loops are possible: in response to a query from adversary A, the world W is allowed to query the adversary’s auxiliary interface \(A_2\); the responding operator may call W in turn, which may call \(A_2\), and so on. Consequently, the event that \(\mathbf{Real} ^{{\varPhi }}_{W/\vec {R}}(A)=1\) (resp. \(\mathbf{Ref} ^{{\varPhi }}_{W/\vec {R}}(A,S)=1\)) must be regarded as the event that the real (resp. reference) experiment halts and outputs 1. Defining advantage this way creates obstacles for quantifying resources of a security reduction, so it will be useful to rule out infinite loops.
We define the class of non-degenerate (n.d.) adversaries as those that respond to main-interface queries using all three oracles—the world’s main interface, the world’s aux.-interface, and the resources—but respond to aux.-interface queries using only the resource oracle. To formalize this behavior, we define n.d. adversaries in terms of an object that is called in response to main-interface queries, and another object that is called in response to aux.-interface queries.
Definition 4
(Non-degenerate adversaries). An adversary A is called non-degenerate (n.d.) if there exist a halting object M that exports an
 -operator and a halting, functional object \( S\!D \) for which \(A=\mathbf{NoDeg} (M, S\!D )\) as specified in Fig. 5. We refer to M as the main algorithm and to \( S\!D \) as the auxiliary algorithm. \(\square \)
-operator and a halting, functional object \( S\!D \) for which \(A=\mathbf{NoDeg} (M, S\!D )\) as specified in Fig. 5. We refer to M as the main algorithm and to \( S\!D \) as the auxiliary algorithm. \(\square \)
Observe that we have also restricted n.d. adversaries so that the main and auxiliary algorithms do not share state; and we have required that the auxiliary algorithm is functional (i.e., deterministic and stateless). These measures are not necessary, strictly speaking, but they will be useful for security proofs. Their purpose is primarily technical, as they do not appear to be restrictive in a practical sense. (They do not limit the primary application considered in this work (§3.2). Incidentally, we note that Rogaway and Stegers make similar restrictions in [46, §5].)
2.3 The Lifting Lemma
The main technical tool of our framework is its lifting lemma, which states that if \(V/\vec {Q}\) is \(\psi \)-secure and \(W/\vec {R}\) is \(\psi \)-indifferentiable from \(V/\vec {Q}\), then \(W/\vec {R}\) is also \(\psi \)-secure. This is a generalization of the main result of MRH, which states that if an object X is secure for a given application and X is indifferentiable from Y, then Y is secure for the same application. In §2.4 we give a precise definition of “application” for which this statement holds.
The Random Oracle Model (ROM). The goal of the lifting lemma is to transform a \(\psi \)-attacker against \(W/\vec {R}\) into a \(\psi \)-attacker against \(V/\vec {Q}\). Indifferentiability is used in the following way: given \(\psi \)-attacker A and simulator S, we construct a \(\psi \)-attacker B and \(\psi \)-differentiator D such that, in the real experiment, D outputs 1 if A wins; and in the reference experiment, D outputs 1 if B wins. Adversary B works by running A in the reference experiment with simulator S: intuitively, if the simulation provided by S “looks like” the real experiment, then B should succeed whenever A succeeds.
This argument might seem familiar, even to readers who have no exposure to the notion of indifferentiability. Indeed, a number of reductions in the provable security literature share the same basic structure. For example, when proving a signature scheme is unforgettable under chosen message attack (UF-CMA), the first step is usually to transform the attacker into a weaker one that does not have access to a signing oracle. This argument involves exhibiting a simulator that correctly answers the UF-CMA adversary’s signing-oracle queries using only the public key (cf. [14, Theorem 4.1]): if the simulation is efficient, then we can argue that security in the weak attack model reduces to UF-CMA. Similarly, to prove a public-key encryption (PKE) scheme is indistinguishable under chosen ciphertext attack (IND-CCA), the strategy might be to exhibit a simulator for the decryption oracle in order to argue that IND-CPA reduces to IND-CCA.
Given the kinds of objects we wish to study, it will be useful for us to accommodate these types of arguments in the lifting lemma. In particular, Lemma 1 considers the case in which one of the resources in the reference experiment is an RO that may be “programmed” by the simulator. (As we discuss in the full version (§A), this capability is commonly used when simulating signing-oracle queries.) In our setting, the RO is programmed by passing it an object M via its
 -operator (2:9–14), which is run by the RO in order to populate the table. Normally we will require M to be an entropy source with the following properties.
-operator (2:9–14), which is run by the RO in order to populate the table. Normally we will require M to be an entropy source with the following properties.
Definition 5
(Sources). Let \(\mu , \rho \ge 0\) be real numbers and \(\mathcal {X}, \mathcal {Y}\) be computable sets. An \(\mathcal {X}\)-source is a stateless object that exports a \((\,)\)-\(\mathbf{elem} _{\mathcal {X}}\)-operator. An \((\mathcal {X}, \mathcal {Y})\)-source is a stateless object that exports a \((\,)\)-\((\mathbf{elem} _{\mathcal {X}\times \mathcal {Y}}, \mathbf{any} )\)-operator. Let M be an \((\mathcal {X},\mathcal {Y})\)-source and let \(((X, Y), \varSigma )\) be random variables distributed according to M. (That is, run \(((x,y), \sigma ) \leftarrow M(\,)\) and assign \(X\leftarrow x\), \(Y\leftarrow y\), and \(\varSigma \leftarrow \sigma \).) We say that M is \((\mu , \rho )\)-min-entropy if the following conditions hold:
-
(1)
For all x and y it holds that \(\Pr \big [\, X = x \,\big ] \le 2^{-\mu }\) and \(\Pr \big [\, Y = y \,\big ] \le 2^{-\rho }\).
-
(2)
For all y and \(\sigma \) it holds that \(\Pr \big [\, Y = y \,\big ] = \Pr \big [\, Y = y \mid \varSigma = \sigma \,\big ]\).
We refer to \(\sigma \) as the auxiliary information (cf. “source” in [9, §3]). \(\square \)
A brief explanation is in order. When a source is executed by an RO, the table T is programmed with the output point (x, y) so that \(T[x]=y\). The auxiliary information \(\sigma \) is returned to the caller (2:14), allowing the source to provide the simulator a “hint” about how the point was chosen. Condition (1) is our min-entropy requirement for sources. We also require condition (2), which states that the range point programmed by the source is independent of the auxiliary information.
Definition 6
(The ROM). Let \(\mathcal {X},\mathcal {Y}\) be computable sets where \(\mathcal {Y}\) is finite, let \(q,p\ge 0\) be integers, and let \(\mu ,\rho \ge 0\) be real numbers. A random oracle from \(\mathcal {X}\) to \(\mathcal {Y}\) with query limit (q, p) is the object \(R=\mathbf{Ro} (\mathcal {X},\mathcal {Y},q,p)\) specified in Fig. 2. This object permits at most q unique RO queries and at most p RO-programming queries. If the query limit is unspecified, then it is \((\infty ,0)\) so that the object permits any number of RO queries but no RO-programming queries. Objects program the RO by making queries matching the pattern
 . An object that makes such queries is called \((\mu , \rho )\)-\((\mathcal {X}, \mathcal {Y})\)-min-entropy if, for all such queries, the object M is always a \((\mu ,\rho )\)-min-entropy \((\mathcal {X},\mathcal {Y})\)-source. An object that makes no queries matching this pattern is not RO-programming (n.r.). \(\square \)
. An object that makes such queries is called \((\mu , \rho )\)-\((\mathcal {X}, \mathcal {Y})\)-min-entropy if, for all such queries, the object M is always a \((\mu ,\rho )\)-min-entropy \((\mathcal {X},\mathcal {Y})\)-source. An object that makes no queries matching this pattern is not RO-programming (n.r.). \(\square \)
To model a function H as a random oracle in an experiment, we revise the experiment by replacing each call of the form “\(H(\,\cdots )\)” with a call of the form “\(\mathcal {R}_i(\,\cdots )\)”, where i is the index of the RO in the shared resources of the experiment, and \(\mathcal {R}\) is the name of the resource oracle. When specifying a cryptographic scheme whose security analysis is in the ROM, we will usually skip this rewriting step and simply write the specification in terms of \(\mathcal {R}_i\)-queries: to obtain the standard model experiment, one would instantiate the i-th resource with H instead of an RO.
We are now ready to state and prove the lifting lemma. Our result accommodates indifferentiability arguments in which the RO might be programmed by the simulator.
Lemma 1 (Lifting)
Let \(\vec {I}=(I_1,\ldots ,I_u),\vec {J}=(J_1,\ldots ,J_v)\) be resources; let \(\mathcal {X},\mathcal {Y}\) be computable sets, where \(\mathcal {Y}\) is finite; let \(N=|\mathcal {Y}|\); let \(\mu ,\rho \ge 0\) be real numbers for which \(\log N\ge \rho \); let \(q,p\ge 0\) be integers; let R and P be random oracles for \(\mathcal {X},\mathcal {Y}\) with query limits \((q+p,0)\) and (q, p) respectively; let W, V be n.r. worlds; and let \(\psi \) be a transcript predicate. For every \(t_A\)-time, \((a_1,a_2,a_r)\)-query, n.d. adversary A and \(t_S\)-time, \((s_2, s_r)\)-query, \((\mu , \rho )\)-\((\mathcal {X}, \mathcal {Y})\)-min-entropy simulator S, there exist n.d. adversaries D and B for which

where \(\varDelta = p\left[ (p+q)/2^{-\mu }+ \sqrt{N/2^{\rho } \cdot \log (N/2^\rho )}\right] \), D is \(O(t_A)\)-time and \((a_1\!+\!1, a_2, a_r)\)-query, and B is \(O(t_At_S)\)-time and \((a_1, a_2s_2, (a_2+a_r)s_r)\)-query.
We leave the proof to the full version of this paper. Apart from dealing with RO programmability, which accounts for the \(\varDelta \)-term in the bound, the proof is essentially the same argument as the sufficient condition in [38, Theorem 1] (cf. [45, Theorem 1]). The high min-entropy of domain points programmed by the simulator ensures that RO-programming queries are unlikely to collide with standard RO queries. However, we will need that range points are statistically close to uniform; otherwise the \(\varDelta \)-term becomes vacuous. Note that \(\varDelta =0\) whenever programming is disallowed.
2.4 Games and the Preservation Lemma
Lemma 1 says that indifferentiability of world W from world V means that security of V implies security of W. This starting point is more general than the usual one, which is to first argue indifferentiability of some system X from another system Y, then use the composition theorem of MRH in order to argue that security of Y for some application implies security of X for the same application. Here we formalize the same kind of argument by specifying the construction of a world from a system X and a game G that defines the system’s security.
A game is a halting object that exports a functional
 -operator. A system is a halting object. Figure 6 specifies the composition of a game G and system X into a world \(W = \mathbf{Wo} (G, X)\) in which the adversary interacts with G’s main interface and X’s auxiliary interface, and G interacts with X’s main interface. The system X makes queries to G’s auxiliary interface, and G in turn makes queries to the adversary’s auxiliary interface. As shown in right hand side of Fig. 6, it is the game that decides whether the adversary has won: when the real experiment calls
-operator. A system is a halting object. Figure 6 specifies the composition of a game G and system X into a world \(W = \mathbf{Wo} (G, X)\) in which the adversary interacts with G’s main interface and X’s auxiliary interface, and G interacts with X’s main interface. The system X makes queries to G’s auxiliary interface, and G in turn makes queries to the adversary’s auxiliary interface. As shown in right hand side of Fig. 6, it is the game that decides whether the adversary has won: when the real experiment calls
 on line 4:4, this call is answered by the operator defined by \(\mathbf{Wo} \) on line 6:3, which returns
on line 4:4, this call is answered by the operator defined by \(\mathbf{Wo} \) on line 6:3, which returns
 .
.
Definition 7
(\(G^{\psi }\) security). Let \(\psi \) be a transcript predicate, G be a game, X be a system, \(\vec {R}\) be resources, and A be an adversary. We define the \(G^{\psi }\) advantage of A in attacking \(X/\vec {R}\) as

We write \(\mathbf{Adv} ^{{G}}_{X/\vec {R}}(A)\) whenever \(\psi ( tx )=1\) for all \( tx \). Informally, we say that \(X/\vec {R}\) is \(G^{\psi }\)-secure if the \(G^{\psi }\) advantage of any efficient adversary is small. \(\square \)
World \(\mathbf{Wo} \) formalizes the class of systems for which we will define security in this paper. While the execution semantics of games and systems seems quite natural, we remark that other ways of capturing security notions are possible. We are restricted only by the execution semantics of the real experiment (Definition 1). Indeed, there are natural classes of security definitions we cannot capture, including those described by multi-stage games [45].
For our particular class of security notions we can prove the following useful lemma. Intuitively, the “preservation” lemma below states that if a system X is \(\psi \)-indifferentiable from Y, then \(\mathbf{Wo} (G,X)\) is \(\psi \)-indifferentiable from \(\mathbf{Wo} (G,Y)\) for any game G. We leave the simple proof to the full version. The main idea is that B in the real (resp. reference) experiment can precisely simulate A’s execution in its real (resp. reference) experiment by using G to answer A’s main-interface queries.
Lemma 2 (Preservation)
Let \(\psi \) be a transcript predicate, X, Y be objects, and \(\vec {R}, \vec {Q}\) be resources. For every \((g_1, \,\underline{}\,)\)-query game G, \(t_A\)-time, \((a_1, a_2, a_r)\)-query, n.d. adversary A, and simulator S there exists an n.d. adversary B such that

where \(W=\mathbf{Wo} (G,X)\), \(V=\mathbf{Wo} (G,Y)\), and B is \(O(t_A)\)-time and \((a_1g_1, a_2, a_r)\)-query.
3 Protocol Translation
In this section we consider the problem of quantifying the security cost of protocol translation, where the real system is obtained from the reference system by modifying the protocol’s specification. As a case study, we design and prove secure a TLS extension for SPAKE2 [3], which, at the time of writing, was one of the PAKEs considered by the CFRG for standardization.
We define security for PAKE in the extended Canetti-Krawczyk (eCK) model of LaMacchia et al. [37], a simple, yet powerful model for the study of authenticated key exchange. The eCK model specifies both the execution environment of the protocol (i.e., how the adversary interacts with it) and its intended goal (i.e., key indistinguishability [13]) in a single security experiment. Our treatment breaks this abstraction boundary.
Recall from the previous section that for any transcript predicate \(\psi \), game G, and systems X and \(\tilde{X}\), we can argue that X is \(G^{\psi }\)-secure (Definition 7) by proving that X is \(\psi \)-indifferentiable from \(\tilde{X}\) (Definition 3) and assuming \(\tilde{X}\) itself is \(G^{\psi }\)-secure. In this section, the system specifies the execution environment of a cryptographic protocol for which the game defines security. In §3.1 we specify a system \(\mathbf{eCK} (\varPi )\) that formalizes the execution of protocol \(\varPi \) in the eCK model. Going up a level of abstraction, running an adversary A in world \(W=\mathbf{Wo} (G,\mathbf{eCK} (\varPi ))\) in the  experiment (Definition 1) lets A execute \(\varPi \) via W’s auxiliary interface and “play” the game G via W’s main interface. The environment \(\mathbf{eCK} \) surfaces information about the state of the execution environment, which G uses to determine if A wins. Finally, transcript predicate \(\psi \) is used to determine if the attack is valid based on the sequence of \(W_1\)- and \(W_2\)-queries made by A.
experiment (Definition 1) lets A execute \(\varPi \) via W’s auxiliary interface and “play” the game G via W’s main interface. The environment \(\mathbf{eCK} \) surfaces information about the state of the execution environment, which G uses to determine if A wins. Finally, transcript predicate \(\psi \) is used to determine if the attack is valid based on the sequence of \(W_1\)- and \(W_2\)-queries made by A.
3.1 eCK-Protocols
The eCK model was introduced by LaMacchia et al. [37] in order to broaden the corruptive powers of the adversary in the Canetti-Krawczyk setting [24]. The pertinent change is to restrict the class of protocols to those whose state is deterministically computed from the player’s static key (i.e., its long-term secret), ephemeral key (i.e., the per-session randomness), and the sequence of messages received so far. This results in a far simpler formulation of session-state compromise. We embellish the syntax by providing the party with an initial input at the start of each session, allowing us to capture features like per-session configuration [17].
Definition 8
(Protocols). An (eCK-)protocol is a halting, stateless object \(\varPi \), with an associated finite set of identities \(\mathcal {I}\subseteq \{0,1\}^*\), that exports the following operators:
-
 : generates the static key and corresponding public key of each party so that \(( pk _i, sk _i)\) is the public/static key pair of party \(i\in \mathcal {I}\).
: generates the static key and corresponding public key of each party so that \(( pk _i, sk _i)\) is the public/static key pair of party \(i\in \mathcal {I}\). -
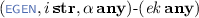 : generates an ephemeral key \( ek \) for party i with input \(\alpha \). The ephemeral key constitutes the randomness used by the party in a given session.
: generates an ephemeral key \( ek \) for party i with input \(\alpha \). The ephemeral key constitutes the randomness used by the party in a given session. -
 : computes the outbound message \( out \) and updated state \(\pi '\) of party i with static key \( sk \), ephemeral key \( ek \), input \(\alpha \), session state \(\pi \), and inbound message \( in \). This operator is deterministic.
: computes the outbound message \( out \) and updated state \(\pi '\) of party i with static key \( sk \), ephemeral key \( ek \), input \(\alpha \), session state \(\pi \), and inbound message \( in \). This operator is deterministic. -
 : indicates the maximum number of moves (i.e., messages sent) in an honest run of the protocol. This operator is deterministic. \(\square \)
: indicates the maximum number of moves (i.e., messages sent) in an honest run of the protocol. This operator is deterministic. \(\square \)
The execution environment for eCK-protocols is specified by \(\mathbf{eCK} \) in Fig. 7. The environment stores the public/static keys of each party (tables \( pk \) and \( sk \)) and the ephemeral key (\( ek \)), input (\(\alpha \)), and current state (\(\pi \)) of each session. As usual, the adversary is responsible for initializing and sending messages to sessions, which it does by making queries to the auxiliary interface (7:14–31). Each session is identified by a pair of strings (s, i), where s is the session index and i is the identity of the party incident to the session. The auxiliary interface exports the following operators:
-
 : initializes session (s, i) on input a by setting \(\alpha _s^i\leftarrow a\) and \(\pi _s^i\leftarrow \bot \). A session initialized in this way is said to be under active attack because the adversary controls its execution.
: initializes session (s, i) on input a by setting \(\alpha _s^i\leftarrow a\) and \(\pi _s^i\leftarrow \bot \). A session initialized in this way is said to be under active attack because the adversary controls its execution. -
 -\(( out \;\mathbf{any} )\): sends message \( in \) to a session (s, i) under active attack. Updates the session state \(\pi _s^i\) and returns the outbound message \( out \).
-\(( out \;\mathbf{any} )\): sends message \( in \) to a session (s, i) under active attack. Updates the session state \(\pi _s^i\) and returns the outbound message \( out \). -
 -\(( tr \;\mathbf{any} )\): executes an honest run of the protocol for initiator session \((s_1, i_1)\) on input \(a_1\) and responder session \((s_0, i_0)\) on input \(a_0\) and returns the sequence of exchanged messages \( tr \). A session initialized this way is said to be under passive attack because the adversary does not control the protocol’s execution.
-\(( tr \;\mathbf{any} )\): executes an honest run of the protocol for initiator session \((s_1, i_1)\) on input \(a_1\) and responder session \((s_0, i_0)\) on input \(a_0\) and returns the sequence of exchanged messages \( tr \). A session initialized this way is said to be under passive attack because the adversary does not control the protocol’s execution. -
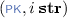 -\(( pk \;\mathbf{any} )\),
-\(( pk \;\mathbf{any} )\), 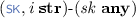 , and
, and
 : returns, respectively, the public key of party i, the static key of party i, and the ephemeral key of session (s, i).
: returns, respectively, the public key of party i, the static key of party i, and the ephemeral key of session (s, i).
Whenever the protocol is executed, it is given access to the adversary’s auxiliary interface (see interface oracle \(\mathcal {A}\) on lines 7:9, 11, 32, and 35). This allows us to formalize security goals for protocols that are only partially specified [46]. In world \(\mathbf{Wo} (G,X)\), system \(X=\mathbf{eCK} (\varPi )\) relays \(\varPi \)’s \(\mathcal {A}\)-queries to G: usually game G will simply forward these queries to the adversary, but the game must explicitly define this. (See the definition of KEY-IND security below in the full version for an example.)
The attack state (\( atk \)) records the sequence of actions carried out by the adversary. Specifically, it records whether each session is under active or passive attack (7:34), whether the adversary knows the ephemeral key of a given session (7:19), and which static keys are known to the adversary (7:17). These are used by the game to decide if the adversary’s attack was successful. In addition, the game is given access to the game state, which surfaces any artifacts computed by a session that are specific to the intended security goal: examples include the session key in a key-exchange protocol, the session identifier (SID) or partner identifier (PID)
[10], or the negotiated mode
[17]. The game state is exposed by the protocol’s
 -interface (e.g., lines 8:8–13). All told, the main interface (7:7–12) exports the following operators:
-interface (e.g., lines 8:8–13). All told, the main interface (7:7–12) exports the following operators:
-
 : initializes each party by running the static key generator and returns the table of public keys \( pk \).
: initializes each party by running the static key generator and returns the table of public keys \( pk \). -
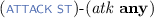 : returns the attack state \( atk \) to the caller.
: returns the attack state \( atk \) to the caller. -
 : provides access to the game state.
: provides access to the game state.
Attack Validity. For simplicity, our execution environment allows some behaviors that are normally excluded in security definitions. Namely, (1) the adversary might initialize a session before the static keys have been generated, or try to generate the static keys more than once; or (2) the adversary might attempt to re-initialize a session already in progress. The first of these is excluded by transcript predicate \(\phi _\mathrm {init}\) and the second by \(\phi _\mathrm {sess}\), both defined below.
Definition 9
(Predicates \(\phi _\mathrm {init}\) and \(\phi _\mathrm {sess}\)). Let \(\phi _\mathrm {init}( tx )=1\) if \(| tx |\ge 1\),
 , and for all \(1 < \alpha \le | tx |\) it holds that
, and for all \(1 < \alpha \le | tx |\) it holds that
 . Let \(\phi _\mathrm {sess}( tx )=0\) iff there exist \(1 \le \alpha < \beta \le | atk |\) such that \( atk _\alpha = (t_\alpha , s_\alpha , i_\alpha )\), \( atk _\beta = (t_\beta , s_\beta , i_\beta )\), \((s_\alpha , i_\alpha ) = (s_\beta , i_\beta )\), and
. Let \(\phi _\mathrm {sess}( tx )=0\) iff there exist \(1 \le \alpha < \beta \le | atk |\) such that \( atk _\alpha = (t_\alpha , s_\alpha , i_\alpha )\), \( atk _\beta = (t_\beta , s_\beta , i_\beta )\), \((s_\alpha , i_\alpha ) = (s_\beta , i_\beta )\), and
 , where \( atk \) is the attack state corresponding to transcript \( tx \). \(\square \)
, where \( atk \) is the attack state corresponding to transcript \( tx \). \(\square \)
3.2 Case Study: PAKE Extension for TLS 1.3
In order to support the IETF’s PAKE-standardization effort, we choose one of the protocols considered by the CFRG and show how to securely integrate it into the TLS handshake. By the time we began our study, the selection process had narrowed to four candidates [52]: SPAKE2 [3], OPAQUE [32], CPace [30], and AuCPace [30]. Of these four, only SPAKE2 has been analyzed in a game-based security model (the rest have proofs in the UC-framework [20]) and as such is the only candidate whose existing analysis can be lifted in our setting. Thus, we choose it for our study.
Existing proposals for PAKE extensions [5, 54] allow passwords to be used either in lieu of certificates or alongside them in order to “hedge” against failures of the web PKI. Barnes and Friel [5] propose a simple, generic extension for TLS 1.3 [44] (draft-barnes-tls-pake) that replaces the standard DH key-exchange with a 2-move PAKE. This straight-forward approach is, arguably, the best option in terms of computational overhead, modularity, and ease-of-implementation. Thus, our goal will be to instantiate draft-barnes-tls-pake with SPAKE2. We begin with an overview of the extension and the pertinent details of TLS. We then describe the SPAKE2 protocol and specify its usage in TLS. We end with our security analysis.
Usage of PAKE with TLS 1.3 (draft-barnes-tls-pake). The TLS handshake begins when the client sends its “ClientHello” message to the server. The server responds with its “ServerHello” followed by its parameters “EncryptedExtensions” and “CertificateRequest” and authentication messages “Certificate”, “CertificateVerify”, and “Finished”. The client replies with its own authentication messages “Certificate”, “CertificateVerify”, and “Finished”. The Hellos carry ephemeral DH key shares signed by the parties’ Certificates, and the signatures are carried by the CertificateVerify messages. Each party provides key confirmation by computing a MAC over the handshake transcript; the MACs are carried by the Finished messages.
The DH shared secret is fed into the “key schedule”
[44, §7.1] that defines the derivation of all symmetric keys used in the protocol. Key derivation uses the \( H\!K\!D\!F \) function
[34], which takes as input a “salt” string, the “initial key material (IKM)” (i.e., the DH shared secret), and an “information” string used to bind derived keys to the context in which they are used in the protocol. The output is used as a salt for subsequent calls to \( H\!K\!D\!F \). The first call is
 , where \(k\ge 0\) is a parameter of TLS called the hash length and \( psk \) is the pre-shared key. (If available, otherwise \( psk =0^k\).) Next, the parties derive the client handshake-traffic key \(K_1\leftarrow H\!K\!D\!F ( salt , dhe , info _1)\), the server handshake-traffic key \(K_0\leftarrow H\!K\!D\!F ( salt , dhe , info _0)\), and the session key
, where \(k\ge 0\) is a parameter of TLS called the hash length and \( psk \) is the pre-shared key. (If available, otherwise \( psk =0^k\).) Next, the parties derive the client handshake-traffic key \(K_1\leftarrow H\!K\!D\!F ( salt , dhe , info _1)\), the server handshake-traffic key \(K_0\leftarrow H\!K\!D\!F ( salt , dhe , info _0)\), and the session key
 . Variable \( dhe \) denotes the shared secret. Each information string encodes both Hellos and a string that identifies the role of the key:
. Variable \( dhe \) denotes the shared secret. Each information string encodes both Hellos and a string that identifies the role of the key:
 for the client and
for the client and
 for the server. The traffic keys are used for encrypting the parameter and authentication messages and computing the Finished MACs, and the session key is used for encrypting application data and computing future pre-shared keys.
for the server. The traffic keys are used for encrypting the parameter and authentication messages and computing the Finished MACs, and the session key is used for encrypting application data and computing future pre-shared keys.
Extensions. Protocol extensions are typically comprised of two messages carried by the handshake: the request, carried by the ClientHello; and the response, carried by the ServerHello or by one of the server’s parameter or authentication messages. Usually the request indicates support for a specific feature and the response indicates whether the feature will be used in the handshake. In draft-barnes-tls-pake, the client sends the first PAKE message in an extension request carried by its ClientHello; if the server chooses to negotiate usage of the PAKE, then it sends the second PAKE message as an extension response carried by its ServerHello. When the extension is used, the PAKE specifies the values of \( psk \) and \( dhe \) in the key schedule.
At first brush, it may seem “obvious” that the security of the extension follows immediately from the security of the PAKE, since the PAKE is run without modification. There are two important points to note here. The first is that the extension is underspecified: the output of a PAKE is generally a single session key, so it is up to the implementer to decide how the session key is mapped to the inputs of the key schedule (i.e., \( psk \) and \( dhe \)). The second point is that the PAKE is not only used to derive the session key (used to protect application data), but also to encrypt handshake messages and compute MACs. As a result, whether this usage is secure or not depends on the concrete protocol and how it is implemented in the extension.
Protocol \(\mathbf {SPake2}\text{- }\mathbf {AP}_{\mathbb {G}}^{\mathcal {C},\mathcal {S}}\), where \(\mathbb {G}=(\mathcal {G},\cdot )\) is a prime-order, cyclic group with generator g and \(\mathcal {S}, \mathcal {C}\subseteq \{0,1\}^*\) are finite, disjoint, non-empty sets. Object \( PW \) is a symmetric password generator for \(\mathcal {S}, \mathcal {C}, \mathcal {P}\) for some dictionary \(\mathcal {P}\subseteq \mathbb {Z}_{|\mathcal {G}|}\).
Protocol \(\mathbf {SPake2}\text{- }\mathbf {TLS}_\mathbb {G}^{\mathcal {C},\mathcal {S}}\), where \( PW \), \(\mathbb {G}=(\mathcal {G},\cdot )\), g, \(\mathcal {C}\), and \(\mathcal {S}\) are as defined in Fig. 8. Object \( en \) is a \(\left( \{0,1\}^*\times \{0,1\}^*\times \mathcal {G}\times \mathcal {G}\times \mathbb {Z}_{|\mathcal {G}|}\times \mathcal {G}\right) \)-encoder, where \(\mathcal {G}\) is a represented set (Definition 10).
The SPAKE2 Protocol. SPAKE2 is the eCK-protocol \(\mathbf {SPake2}\text{- }\mathbf {AP}^{\mathcal {C},\mathcal {S}}_\mathbb {G}( PW )\) in Fig. 8 (cf. [1, Figure 1]). (Refer to the full version for a detailed explanation.) Sets \(\mathcal {C}\) and \(\mathcal {S}\) denote the clients and servers respectively. Key derivation is carried out by a call to \(\mathcal {R}_1\). To obtain the concrete protocol, one would use the hash function H to instantiate the first resource in the experiment. However, since all existing analyses model H as an RO [1, 3, 6], we will also use an RO. (See Theorem 1 below.)
The protocol is parameterized by an object \( PW \) used to generate the static keys. Syntactically, we require that \( PW \) halts and outputs a table \( sk \) for which \( sk [s][c] = sk [c] \in \mathcal {P}\) for all \((c, s) \in \mathcal {C}\times \mathcal {S}\) and some set \(\mathcal {P}\subseteq \mathbb {Z}_{|\mathcal {G}|}\), called the dictionary. We refer to such an object as a symmetric password generator for \(\mathcal {C},\mathcal {S},\mathcal {P}\). Following Bellare et al. [10], each client c is in possession of a single password \( sk [c]\in \mathcal {P}\), used to authenticate to each server; and each server s is in possession of a table \( sk [s]\) that stores the password \( sk [s][c]\) shared with each client c. Generally speaking—and for SPAKE2 in particular [1, 3, 6]—passwords are assumed to be uniformly and independently distributed over the dictionary \(\mathcal {P}\). We call such a generator uniform.
Securely Instantiating draft-barnes-tls-pake with SPAKE2. In Fig. 9 we define a protocol \(\mathbf {SPake2}\text{- }\mathbf {TLS}^{\mathcal {C},\mathcal {S}}_\mathbb {G}( PW , const _1, const _0)\) that partially specifies the usage of SPAKE2 in TLS. We say “partially” because most of the details of TLS are provided by calls to interface oracle \(\mathcal {A}\), which are answered by the adversary’s auxiliary interface in the real experiment. Calls to \(\mathcal {R}_1\) and \(\mathcal {R}_2\) are answered by, respectively, an RO for \( H\!K\!D\!F \) and an RO for a function \(H_\mathbb {G}\), defined below. Before being passed to \( H\!K\!D\!F \), the input is first encoded using an object \( en \) with the following properties.
Definition 10
(Encoders and represented sets). A represented set is a computable set \(\mathcal {X}\) for which \(\bot \not \in \mathcal {X}\) (cf. “represented groups” in [2, §2.1]). Let \(\mathcal {X}\) be a represented set. An \(\mathcal {X}\)-encoder is a functional, halting object \( en \) that exports the following operators:
-
\((1, x\;\mathbf{elem} _{\mathcal {X}})\)-\((M \;\mathbf{str} )\): the encoding algorithm, returns the encoding M of x as a string.
-
\((0, M\;\mathbf{str} )\)-\((x\;\mathbf{elem} _{\mathcal {X}\cup \{\bot \}})\): the decoding algorithm, returns the element x of \(\mathcal {X}\) encoded by string M (or \(\bot \) if M does not encode an element of \(\mathcal {X}\)).
Correctness requires that \( en _0( en _1(x))=x\) for every \(x\in \mathcal {X}\). \(\square \)
The Hellos carry the SPAKE2 key-exchange messages. The first is encoded by the client on line 9:22 and decoded by the server on line 39, and the second is encoded by the server on line 42 and decoded by the client on line 28. Value \( ikm \) (the input to H in SPAKE2) is passed to procedure \(\mathbf{KDF} \) (54–65), which is used to derive the traffic and session keys. Oracle \(\mathcal {A}\) (which points to the adversary’s aux. interface in the security experiment) chooses the salt and information strings, subject to the constraint that the information strings are distinct.
We refer to the ClientHello as HELLO1 and to the ServerHello as HELLO0. Our spec lumps all other handshake messages into two: AUTH0 for the server’s parameter and authentication messages (EncryptedExtensions...Finished); and AUTH1 for the client’s authentication messages (Certificate...Finished). This consolidates all traffic-key dependent computations into four \(\mathcal {A}\)-queries: AUTH0 is computed on line 9:45 and verified on line 32 and AUTH1 is computed on line 33 and verified on line 50. In the full version we include a detailed explanation of Fig. 9 and design rationale for the extension. One notable feature is that instead of relying on trusted setup to generate the public parameters \(N_1, N_0 \in \mathbb {G}\), we pick two distinct constants \( const _1, const _0\in \{0,1\}^*\) and compute the parameters as \(N_1\leftarrow H_\mathbb {G}( const _1)\) and \(N_0\leftarrow H_\mathbb {G}( const _0)\), where \(H_\mathbb {G}:\{0,1\}^*\rightarrow \mathcal {G}\) is a hash function suitable for the given group \(\mathbb {G}=(\mathcal {G},\cdot )\) (e.g., a suitable “hash-to-curve” algorithm [28]).
Security. We now derive the concrete security of this usage of SPAKE2. Our analysis is in the weak corruption model of Bellare et al. [10], which assumes that only static keys (i.e., passwords) and not ephemeral keys can be revealed to the attacker. This is without loss of generality, as all existing analyses of SPAKE2 assume the same corruption model [1, 3, 6]. Our proof also uses the GDH assumption [39], defined below.
Definition 11
(Predicate \(\phi _\mathrm {wc}\)). Let
 . \(\square \)
. \(\square \)
Definition 12
(The GDH problem). Let \(\mathbb {G}= (\mathcal {G}, \cdot )\) be a cyclic group with generator \(g\in \mathcal {G}\). A DDH oracle for \(\mathbb {G}\) is a halting object \( D\!D\!H \) for which \( D\!D\!H (X,Y,Z)=1\) holds if and only if \(\log _g X \cdot \log _g Y = \log _g Z\) for all \(X,Y,Z\in \mathcal {G}\). Define
 to be the advantage of an adversary A in solving the GDH problem for \(\mathbb {G}\). Informally, we say the GDH problem is hard for \(\mathbb {G}\) if the advantage of every efficient adversary is small. \(\square \)
to be the advantage of an adversary A in solving the GDH problem for \(\mathbb {G}\). Informally, we say the GDH problem is hard for \(\mathbb {G}\) if the advantage of every efficient adversary is small. \(\square \)
Let \(k\ge 0\) be an integer; let \( const _1, const _0\) be distinct strings; let \(\mathbb {G}=(\mathcal {G}, \cdot )\) be a prime-order cyclic group; let \(\mathcal {C}, \mathcal {S}\subseteq \{0,1\}^*\) be finite, disjoint, non-empty sets; let \(\mathcal {P}\subseteq \mathbb {Z}_{|\mathcal {G}|}\) be a dictionary; and let \( PW \) be a uniform, symmetric password-generator for \(\mathcal {C}, \mathcal {S}, \mathcal {P}\). Define \(\mathcal {T}\) to be the set \(\{0,1\}^*\times \{0,1\}^*\times \mathcal {G}\times \mathcal {G}\times \mathbb {Z}_{|\mathcal {G}|}\times \mathcal {G}\). Let \(\varPi =\mathbf {SPake2}\text{- }\mathbf {TLS}_\mathbb {G}^{\mathcal {C},\mathcal {S}}( PW , const _1, const _0)\), \(\tilde{\varPi }=\mathbf {SPake2}\text{- }\mathbf {AP}_\mathbb {G}^{\mathcal {C},\mathcal {S}}( PW )\), \(X = \mathbf{eCK} (\varPi )\), and \(\tilde{X} = \mathbf{eCK} (\tilde{\varPi })\). Let \(\psi = \phi _\mathrm {init}\wedge \phi _\mathrm {sess}\wedge \phi _\mathrm {wc}\). The following says that for any game G, the \(G^{\psi }\)-security of X (in the ROM for \( H\!K\!D\!F \) and \(H_\mathbb {G}\)) follows from the \(G^{\psi }\)-security of \(\tilde{X}\) (in the ROM for H) under the GDH assumption.
Theorem 1
Let F be an RO from \((\{0,1\}^*)^3\) to \(\{0,1\}^k\), R be an RO from \(\{0,1\}^*\) to \(\mathcal {G}\), and H be an RO from \(\mathcal {T}\) to \(\{0,1\}^k\). Let \( D\!D\!H \) be a DDH oracle for \(\mathbb {G}\). For every game G and \(t_A\)-time, n.d. adversary A making \(q_r\) resource queries, \(q_s\)
 , and \(q_e\)
, and \(q_e\)
 -queries, there exist an n.d. adversary B and GDH-adversary C such that
-queries, there exist an n.d. adversary B and GDH-adversary C such that
where: \( D\!D\!H \) is \(t_{ D\!D\!H }\)-time; B runs in time \(O(\hat{T})\) and makes at most \(q_s\)
 , \(q_e\)
, \(q_e\)
 -queries, \(O(\hat{Q})\) \( D\!D\!H \)-queries, and \(q_r\) H-queries; C runs in time \(O(\hat{T})\) and makes at most \(O(\hat{Q})\) \( D\!D\!H \)-queries; \(\hat{T} = t_A(t_A + q_r \cdot t_{ D\!D\!H })\); and \(\hat{Q} = q_r(q_s+q_e)\).
-queries, \(O(\hat{Q})\) \( D\!D\!H \)-queries, and \(q_r\) H-queries; C runs in time \(O(\hat{T})\) and makes at most \(O(\hat{Q})\) \( D\!D\!H \)-queries; \(\hat{T} = t_A(t_A + q_r \cdot t_{ D\!D\!H })\); and \(\hat{Q} = q_r(q_s+q_e)\).
We leave the proof to the full version but sketch the main ideas here. The claim is proved by first applying Lemma 1, then applying Lemma 2 so that we can argue security using the \(\psi \)-indifferentiability of \(X/(F,R)\) from \(\tilde{X}/(H, D\!D\!H )\). The bound reflects the loss in security that results from using the PAKE to derive the traffic keys. The GDH-advantage term is used to bound the probability that derivation of one of these keys during an honest run of the protocol (via
 ) coincides with a previous RO query; the \(2q_s/|\mathcal {P}|\)-term is used to bound the probability of the same event occurring during an active attack (via
) coincides with a previous RO query; the \(2q_s/|\mathcal {P}|\)-term is used to bound the probability of the same event occurring during an active attack (via
 ). The simulator kills a session if the SID ever collides with another session other than the partner, which accounts for the final term.
). The simulator kills a session if the SID ever collides with another session other than the partner, which accounts for the final term.
Given a non-degenerate, \(\psi \)-differentiator D, the goal is to exhibit an efficient simulator S and GDH-adversary C that yield the result. Recall that S gets two oracles in the reference experiment: one for the aux. interface of \(\tilde{X}\), which is used to execute the reference protocol \(\tilde{\varPi }\); and another for resources \((H, D\!D\!H )\). Its job is to simulate aux./resource queries for \(X/(F,R)\). The central problem it must solve is that the adversary has direct access to the main interface of \(\tilde{X}\), which provides it with the game and attack state. Hence, the adversary needs to use its own oracles in a way that ensures the game and attack state are consistent with the adversary’s view of the execution.
Refer to S’s oracles as \(\mathcal {X}\) and \(\mathcal {R}\). Its strategy is to “embed” a run of the reference protocol into each simulation of the real one so that each
 or
or
 from the adversary is mapped to an
from the adversary is mapped to an
 or
or
 to \(\mathcal {X}\). RO queries are simulated by S itself, except that \(\mathcal {R}_1\) (points to H) is called whenever the query coincides with the derivation of a session key. The \( D\!D\!H \) oracle (pointed to by \(\mathcal {R}_2\)) is used to determine if this is the case. The difficult part is simulating computation of the traffic keys without knowing the password and/or shared secret. In a nutshell, the strategy is to “guess” that the adversary has not yet made an RO query that coincides with these, generate fresh keys, then back-patch the RO simulation in order to ensure consistency going forward.
to \(\mathcal {X}\). RO queries are simulated by S itself, except that \(\mathcal {R}_1\) (points to H) is called whenever the query coincides with the derivation of a session key. The \( D\!D\!H \) oracle (pointed to by \(\mathcal {R}_2\)) is used to determine if this is the case. The difficult part is simulating computation of the traffic keys without knowing the password and/or shared secret. In a nutshell, the strategy is to “guess” that the adversary has not yet made an RO query that coincides with these, generate fresh keys, then back-patch the RO simulation in order to ensure consistency going forward.
Notes
- 1.
Cryptography Forum Research Group.
- 2.
Internet Engineering Task Force.
References
Abdalla, M., Barbosa, M.: Perfect forward security of SPAKE2. Cryptology ePrint Archive, Report 2019/1194 (2019). https://eprint.iacr.org/2019/1194
Abdalla, M., Bellare, M., Rogaway, P.: The oracle Diffie-Hellman assumptions and an analysis of DHIES. In: Naccache, D. (ed.) CT-RSA 2001. LNCS, vol. 2020, pp. 143–158. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45353-9_12
Abdalla, M., Pointcheval, D.: Simple password-based encrypted key exchange protocols. In: Menezes, A. (ed.) CT-RSA 2005. LNCS, vol. 3376, pp. 191–208. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30574-3_14
Barbosa, M., Farshim, P.: Indifferentiable authenticated encryption. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10991, pp. 187–220. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_7
Barnes, R., Friel, O.: Usage of PAKE with TLS 1.3. Internet-Draft draft-barnes-tls-pake-04, Internet Engineering Task Force (2018). https://datatracker.ietf.org/doc/html/draft-barnes-tls-pake-04
Becerra, J., Ostrev, D., Škrobot, M.: Forward secrecy of SPAKE2. In: Baek, J., Susilo, W., Kim, J. (eds.) ProvSec 2018. LNCS, vol. 11192, pp. 366–384. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-01446-9_21
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: Proceedings 38th Annual Symposium on Foundations of Computer Science, pp. 394–403 (1997). https://doi.org/10.1109/SFCS.1997.646128
Bellare, M., Davis, H., Günther, F.: Separate your domains: NIST PQC KEMs, oracle cloning and read-only indifferentiability. Cryptology ePrint Archive, Report 2020/241 (2020). https://eprint.iacr.org/2020/241
Bellare, M., Keelveedhi, S., Ristenpart, T.: Message-locked encryption and secure deduplication. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 296–312. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_18
Bellare, M., Pointcheval, D., Rogaway, P.: Authenticated key exchange secure against dictionary attacks. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 139–155. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_11
Bellare, M., Ristenpart, T., Tessaro, S.: Multi-instance security and its application to password-based cryptography. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 312–329. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_19
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Proceedings of the 1st ACM Conference on Computer and Communications Security, CCS 1993, pp. 62–73. ACM, New York (1993)
Bellare, M., Rogaway, P.: Entity authentication and key distribution. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 232–249. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_21
Bellare, M., Rogaway, P.: The exact security of digital signatures-how to sign with RSA and Rabin. In: Maurer, U. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 399–416. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68339-9_34
Bellare, M., Rogaway, P.: Code-based game-playing proofs and the security of triple encryption. Cryptology ePrint Archive, Report 2004/331 (2004). https://eprint.iacr.org/2004/331
Bellovin, S.M., Merritt, M.: Encrypted key exchange: password-based protocols secure against dictionary attacks. In: Proceedings 1992 IEEE Computer Society Symposium on Research in Security and Privacy, pp. 72–84 (1992). https://doi.org/10.1109/RISP.1992.213269
Bhargavan, K., Brzuska, C., Fournet, C., Green, M., Kohlweiss, M., Zanella-Béguelin, S.: Downgrade resilience in key-exchange protocols. In: 2016 IEEE Symposium on Security and Privacy, pp. 506–525 (2016). https://doi.org/10.1109/SP.2016.37
Bhargavan, K.: Review of the balanced PAKE proposals. Mail to IRTF CFRG, September 2019 (2019). https://mailarchive.ietf.org/arch/msg/cfrg/5VhZLYGpzU8MWPlbMr2cf4Uc-nI
Boldyreva, A., Degabriele, J.P., Paterson, K.G., Stam, M.: Security of symmetric encryption in the presence of ciphertext fragmentation. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 682–699. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_40
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. Cryptology ePrint Archive, Report 2000/067 (2000). https://eprint.iacr.org/2000/067
Canetti, R., Dodis, Y., Pass, R., Walfish, S.: Universally composable security with global setup. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 61–85. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_4
Canetti, R., Fischlin, M.: Universally composable commitments. Cryptology ePrint Archive, Report 2001/055 (2001). https://eprint.iacr.org/2001/055
Canetti, R., Halevi, S., Katz, J., Lindell, Y., MacKenzie, P.: Universally composable password-based key exchange. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 404–421. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_24
Canetti, R., Krawczyk, H.: Analysis of key-exchange protocols and their use for building secure channels. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 453–474. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_28
Cash, D., Kiltz, E., Shoup, V.: The Twin Diffie-Hellman problem and applications. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 127–145. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_8
Coron, J.-S., Dodis, Y., Malinaud, C., Puniya, P.: Merkle-Damgård revisited: how to construct a hash function. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 430–448. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_26
Coron, J.S., Holenstein, T., Künzler, R., Patarin, J., Seurin, Y., Tessaro, S.: How to build an ideal cipher: the indifferentiability of the Feistel construction. J. Cryptol. 29(1), 61–114 (2016). https://doi.org/10.1007/s00145-014-9189-6
Faz-Hernandez, A., Scott, S., Sullivan, N., Wahby, R.S., Wood, C.A.: Hashing to elliptic curves. Internet-Draft draft-irtf-cfrg-hash-to-curve-07, Internet Engineering Task Force (2020). https://datatracker.ietf.org/doc/html/draft-irtf-cfrg-hash-to-curve-07
Fischlin, M., Lehmann, A., Ristenpart, T., Shrimpton, T., Stam, M., Tessaro, S.: Random oracles with(out) programmability. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 303–320. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_18
Haase, B., Labrique, B.: AuCPace: Efficient verifier-based PAKE protocol tailored for the IIoT. Cryptology ePrint Archive, Report 2018/286 (2018). https://eprint.iacr.org/2018/286
Haber, S., Pinkas, B.: Securely combining public-key cryptosystems. In: Proceedings of the 8th ACM Conference on Computer and Communications Security, CCS 2001, pp. 215–224. ACM, New York (2001)
Jarecki, S., Krawczyk, H., Xu, J.: OPAQUE: an asymmetric PAKE protocol secure against pre-computation attacks. Cryptology ePrint Archive, Report 2018/163 (2018). https://eprint.iacr.org/2018/163
Kotzias, P., Razaghpanah, A., Amann, J., Paterson, K.G., Vallina-Rodriguez, N., Caballero, J.: Coming of age: a longitudinal study of TLS deployment. In: Proceedings of the Internet Measurement Conference 2018, IMC 2018, pp. 415–428. Association for Computing Machinery, New York (2018). https://doi.org/10.1145/3278532.3278568
Krawczyk, D.H., Eronen, P.: HMAC-based extract-and-expand key derivation function (HKDF). RFC 5869 (2010). https://rfc-editor.org/rfc/rfc5869.txt
Krawczyk, H., Wee, H.: The OPTLS protocol and TLS 1.3. In: 2016 IEEE European Symposium on Security and Privacy, pp. 81–96 (2016). https://doi.org/10.1109/EuroSP.2016.18
Ladd, W., Kaduk, B.: SPAKE2, a PAKE. Internet-Draft draft-irtf-cfrg-spake2-10, Internet Engineering Task Force (2020). https://datatracker.ietf.org/doc/html/draft-irtf-cfrg-spake2-10
LaMacchia, B., Lauter, K., Mityagin, A.: Stronger security of authenticated key exchange. In: Susilo, W., Liu, J.K., Mu, Y. (eds.) ProvSec 2007. LNCS, vol. 4784, pp. 1–16. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-75670-5_1
Maurer, U., Renner, R., Holenstein, C.: Indifferentiability, impossibility results on reductions, and applications to the random oracle methodology. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 21–39. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_2
Okamoto, T., Pointcheval, D.: The gap-problems: a new class of problems for the security of cryptographic schemes. In: Kim, K. (ed.) PKC 2001. LNCS, vol. 1992, pp. 104–118. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44586-2_8
Paterson, K.G., van der Merwe, T.: Reactive and proactive standardisation of TLS. In: Chen, L., McGrew, D., Mitchell, C. (eds.) SSR 2016. LNCS, vol. 10074, pp. 160–186. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-49100-4_7
Patton, C., Shrimpton, T.: Security in the presence of key reuse: Context-separable interfaces and their applications. Cryptology ePrint Archive, Report 2019/519 (2019). https://eprint.iacr.org/2019/519
Patton, C., Shrimpton, T.: Quantifying the security cost of migrating protocols to practice. Cryptology ePrint Archive, Report 2020/573 (2020). https://eprint.iacr.org/2020/573
Pollard, J.M.: Kangaroos, monopoly and discrete logarithms. J. Cryptol. 13(4), 437–447 (2000). https://doi.org/10.1007/s001450010010
Rescorla, E.: The Transport Layer Security (TLS) protocol version 1.3. RFC 8446 (2018). https://rfc-editor.org/rfc/rfc8446.txt
Ristenpart, T., Shacham, H., Shrimpton, T.: Careful with composition: limitations of the indifferentiability framework. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 487–506. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_27
Rogaway, P., Stegers, T.: Authentication without elision: Partially specified protocols, associated data, and cryptographic models described by code. In: 2009 22nd IEEE Computer Security Foundations Symposium, pp. 26–39 (2009)
Rogaway, P., Zhang, Y.: Simplifying game-based definitions. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 3–32. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_1
Schnorr, C.P.: Efficient signature generation by smart cards. J. Cryptol. 4(3), 161–174 (1991). https://doi.org/10.1007/BF00196725
Shoup, V.: Security analysis of SPAKE2+. Cryptology ePrint Archive, Report 2020/313 (2020). https://eprint.iacr.org/2020/313
Skrobot, M., Lancrenon, J.: On composability of game-based password authenticated key exchange. In: 2018 IEEE European Symposium on Security and Privacy, pp. 443–457 (2018). https://doi.org/10.1109/EuroSP.2018.00038
Smyshlyaev, S.: Overview of existing PAKEs and PAKE selection criteria. IETF 104 (2019). https://datatracker.ietf.org/meeting/104/materials/slides-104-cfrg-pake-selection
Smyshlyaev, S.: Round 2 of the PAKE selection process. Mail to IRTF CFRG, September 2019 (2019). https://mailarchive.ietf.org/arch/msg/cfrg/-a1sW3jK_5avmb98zmFbCNLmpAs
Stevens, M., Bursztein, E., Karpman, P., Albertini, A., Markov, Y.: The first collision for full SHA-1. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 570–596. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_19
Sullivan, N., Krawczyk, D.H., Friel, O., Barnes, R.: Usage of OPAQUE with TLS 1.3. Internet-Draft draft-sullivan-tls-opaque-00, Internet Engineering Task Force (2019). https://datatracker.ietf.org/doc/html/draft-sullivan-tls-opaque-00, Work in progress
Tackmann, B.: PAKE review. Mail to IRTF CFRG, October 2019 (2019). https://mailarchive.ietf.org/arch/msg/cfrg/1sNu9USxo1lnFdzCL5msUFKBjzM
Acknowledgements
Funding for this work was provided by NSF grant CNS-1816375. We thank the anonymous reviewers of CRYPTO 2020 for their useful comments.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Patton, C., Shrimpton, T. (2020). Quantifying the Security Cost of Migrating Protocols to Practice. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12170. Springer, Cham. https://doi.org/10.1007/978-3-030-56784-2_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-56784-2_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56783-5
Online ISBN: 978-3-030-56784-2
eBook Packages: Computer ScienceComputer Science (R0)






 (Definition
(Definition  (Definition
(Definition 




 : generates the static key and corresponding public key of each party so that
: generates the static key and corresponding public key of each party so that 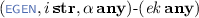 : generates an ephemeral key
: generates an ephemeral key  : computes the outbound message
: computes the outbound message  : indicates the maximum number of moves (i.e., messages sent) in an honest run of the protocol. This operator is deterministic.
: indicates the maximum number of moves (i.e., messages sent) in an honest run of the protocol. This operator is deterministic. 
 : initializes session (s, i) on input a by setting
: initializes session (s, i) on input a by setting  -
- -
-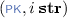 -
-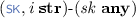 , and
, and
 : returns, respectively, the public key of party i, the static key of party i, and the ephemeral key of session (s, i).
: returns, respectively, the public key of party i, the static key of party i, and the ephemeral key of session (s, i). : initializes each party by running the static key generator and returns the table of public keys
: initializes each party by running the static key generator and returns the table of public keys 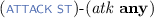 : returns the attack state
: returns the attack state  : provides access to the game state.
: provides access to the game state.

