Abstract
We describe two very efficient polynomial-time algorithms for reducing module lattices defined over arbitrary cyclotomic fields that solve the \(\gamma \)-Hermite Module-SVP problem. They both exploit the structure of tower fields and the second one also uses the symplectic geometry existing in these fields. We conjecture that a rank-2 module over a cyclotomic field of degree n with B-bit coefficients can be heuristically reduced within approximation factor \(2^{\widetilde{\text {O}}\left( n\right) }\) in time \(\widetilde{\text {O}}\left( n^2B\right) \). In the symplectic algorithm, if the condition number C of the input matrix is large enough, this complexity shrinks to \(\widetilde{\text {O}}\left( n^{\log _2 3}C\right) \). In cryptography, matrices are well-conditioned and we can take \(C=B\), but in the worst case, C can be as large as nB. This last result is particularly striking as for some matrices, we can go below the \(n^2B\) swaps lower bound given by the analysis of LLL based on the potential. These algorithms are parallel and we provide a full implementation. We apply them on multilinear cryptographic concrete parameters by reducing matrices of dimension 4096 with 6675-bit integers in 4 days. Finally, we give a quasicubic time for the Gentry-Szydlo algorithm and run it in dimension 1024. It requires efficient ideal multiplications which need fast lattice reductions.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Lenstra, Lenstra, and Lovász introduced in 1984 the lll-algorithm to reduce lattice basis over the euclidean ring \(\mathbf {Z}\) [27] in polynomial time. Nowadays, it is of utmost importance to extend it to non-euclidean rings. Indeed, most lattice-based cryptosystems proposed at the NIST Post-Quantum competition base their security on the assumed hardness of reducing structured lattices, a.k.a. ideal or module lattices [25, 29]. More specifically, they relies on the average-case/hard-case problems, learning with errors (lwe) [39] and short integer solution (sis) [1] problems, which have been proved to be as hard as solving worst-case instances of lattice problems, such as finding a god basis. Furthermore, these ideal or module lattices are usually defined over the integer rings \(\mathcal {O}_{\mathbf {K}}\) of a power of two cyclotomic number fields \(\mathbf {K}\) for efficiency and storage considerations. These structured lattices represent apparently easier instances than random lattice instances, but they also enjoy worst-case / average-case reductions. Module lattices are closer to random lattices than ideal lattices and allow better efficiency/security tradeoff. Currently, it is widely believed that there is no weakness in using structured lattices compared to random lattices.
An n-dimensional lattice is a discrete subgroup of \(\mathbf {R}^n\) and reducing a lattice consists of finding a basis with short and nearly orthogonal vectors. Reducing lattices of high dimensions is a notoriously hard problem and we do not know how to solve it efficiently. Many hard problems have been defined on lattices and even finding a shortest non-zero vector is difficult. The lll algorithm allows solving approximate versions of these two problems, Short Independent Vectors Problem (sivp) and Shortest Vector Problem (svp) within an exponential factor in the lattice dimension. In [27], Lenstra et al. show how to reduce lattices of dimension n by using a reduction algorithm for 2-dimensional lattices. For 2-dimensional euclidean lattice, Lagrange algorithm outputs optimal basis: the two output vectors achieve the minima of the lattice, smallest elements in independent directions. lll outputs a basis of (relatively) good quality in polynomial time and the first vector of the basis lies within an exponential factor approximation of a shortest non-zero vector. Yet, the approximation factor is very large, exponential in the dimension. Many algorithms such as bkz [41] or other reductions (hkz [20], slide [12]) have been proposed to improve the approximation factor of the basis. In another direction, some papers have improved the running time analysis of lll: starting from the quadratic lll algorithm of Nguyen and Stehlé [36] in \(O(n^3(n+B)B\cdot M(n))\), where M(k) is the complexity of multiplying k-bit integers, using a nice numerical analysis for floating-point arithmetic (the algorithm is quadratic in B the number of bits of the input matrix), to the quasi-linear complexity, \(O(n^{5+\epsilon }B+n^{\omega +1+\epsilon }B^{1+\epsilon })\), where \(\epsilon >0\) and \(\omega \) is the exponent for matrix multiplication of [37] and more recently the \(O(n^{4+\epsilon }B^{1+\epsilon })\) algorithm of Neumaier and Stehlé [35]. The two last algorithms do not only improve the analysis, they also make significant changes and are recursive algorithms. While [37] consider various precisions at each step of the algorithm, the way how we choose the sublattices to recurse also changes the behavior of the algorithm: for example [35] has a strategy close to bkz passes. Since the analysis follows bkz analysis [16], the upper bound is only given for the first vector and not all vectors. The main consequence is that we have a bound relative to the volume of the lattice and not the shortest vector.
In cryptography, we often need to reduce lattices of dimension several thousand with thousand of bits. Such lattices arise in Coppersmith cryptanalysis [8], in fhe or multilinear map. To reduce them, we absolutely need an lll implementation linear in the bitlength B and with the smallest exponent in the dimension. For fhe and multilinear map, the approximation factor is not the most important parameter and some fhe parameters have been set by using the lll complexity.
Reduction and cryptanalysis over number fields. The first generalization of lll for number fields has been proposed by Napias [33]. She described such an algorithm for norm-Euclidean rings or orders. It works for cyclotomic rings up to \(n=8\). This algorithm has been extended by Kim and Lee in [21] for biquadratic fields if their rings of integers are norm-Euclidean; meaning that it is a Euclidean domain for the algebraic norm.
For other number fields, the natural solution is the following. A 2-rank module is defined by a 2-by-2 matrix with coefficients in \(\mathcal {O}_{\mathbf {K}}\). Each coefficient in \(\mathcal {O}_{\mathbf {K}}\) can be transformed to a n-by-n matrix over \(\mathbf {Z}\) representing the multiplication by \(\alpha \) in \(\mathcal {O}_{\mathbf {K}}\). Therefore, the module can also be defined by a (2n)-dimensional matrix over \(\mathbf {Z}\). Once we get a lattice over \(\mathbf {Z}\), one can apply the lll algorithm which will output a \(2^{2n}\)-approximation of a shortest non-zero vector in polynomial time in n. The multiplication by n in the dimension rules out every practical computation for cryptographic instances. The problem with this approach is that it forgets completely the geometry of the underlying number fields. Our approach consists in reducing the matrix M directly over \(\mathcal {O}_{\mathbf {K}}\). In [26], Lee et al. show a reduction between the computation of d-dimensional modules and the apparently simpler task of reducing rank-2 modules in general number fields. It is well-known by cryptanalysts that the 2-dimensional case already captures the inherent difficulty since it is the basic case in ntru key recovery. By restricting to cyclotomic fields rather than general number fields as it is proposed in [26], we avoid one important problem: generally speaking, modules are not defined by basis but by pseudo-basis which makes things harder. Moreover, the use of cyclotomic fields always enables us to simplify some steps. In the reduction step, we have to find an element in \(\mathcal {O}_{\mathbf {K}}\) close to an element in \(\mathbf {K}\). Lee et al. propose a technique to circumvent this problem, while it is known that by using Cramer et al. result in cyclotomic fields [9], one can solve it efficiently.
The lattice reduction of ntru shares some interesting connections with the reduction of lattice defined over cyclotomic fields. First of all, Gama et al. in [11] propose a new lattice reduction algorithm for ntru lattice, called symplectic reduction. They observe that it is possible to speed up by a factor 2 the computation by using symmetries in the ntru basis as the second half of the basis can be obtained for free from the first part. Let \(J_{2n}\) be a 2-by-2 matrix:
This is a skew-symmetric matrix of determinant 1 such that \(J_{2n}^2=-\text {Id}_{2n}\). A (2n)-by-(2n) matrix M is symplectic if \(M^t J_{2n} M = J_{2n}\), i.e. the matrix M keep invariant the quadratic form \(J_{2n}\). The ntru public key is a symplectic matrix. In [11], they show that there exist transformations to reduce a basis that keeps the symplecticity of the matrix over \(\mathbf {Z}\). The speed-up factor comes from the fact that some computations can be avoided as the Gram-Schmidt vectors satisfy the relations: \(b^*_{2n+1-i}=\frac{1}{\Vert b_i^*\Vert }b_i^*J_{2n}\). This symmetry is present in all cyclotomic fields we considered and at each recursion level. Secondly, Albrecht et al. [2] show how one can exploit subfields to solve overstretched versions of the ntru cryptosystems used in fhe schemes. In [38], Pornin et Prest improve the runtime of ntru-based cryptosystems key generation by using a recursive algorithm in subfields. It is a generalization of the Extended Euclidean Algorithm to towers of cyclotomic fields and is a one-dimensional case of the lattice reduction problem.
Our contributions. In this work, we present two algorithms and conjecture their complexity. To assess these conjectures, we give a first rough analysis with more detailed information in [23]. We stress here that our aim is not to provide a full analysis of the running time in a floating-point computational model but to give evidence for the asymptotic behavior of our algorithms. To achieve these complexities, it is crucial to consider the precision used at each level of the recursion as when we descend in the recursion tree, the number of bits of the elements increases. The analysis follows the principle of the bkz analysis by Hanrot et al. [16] which explains why we solve the \(\gamma \)-Hermite Module-svp problem. Furthermore, we are interested in reducing matrices frequently encountered by cryptanalysts and not in worst-case instances. It is neither a worst-case analysis nor an average case, but these complexities are important to estimate the runtime on cryptographic instances. Besides, they conform rather well with our experiments and the size of the instances we have reduced. Finally, our implementation is in gp and is parallelized. If one is interested in the hidden constants in the big-O notation, it is worth implementing it in a low-level language.
Claim 1
(Informal). Over a cyclotomic field of degree n and sufficiently smooth conductor, one can reduce a rank-2 module represented as a 2-by-2 matrix M whose number of bits in the input coefficients is uniformly bounded by \(B>n\), in time \(\widetilde{\text {O}}\left( n^2B\right) \) heuristically. The first column of the reduced matrix has its coefficients uniformly bounded by

The second algorithm fully exploits the symplectic structure of these lattices. It is polynomial in the condition number of the input matrix, with a dimensional factor below the classical bound in \(n^2\). As the condition number is expected to be large, the second term component is negligible in most cases.
Claim 2
(Informal). For cyclotomic fields with power of prime q conductor n, with the smoothness condition \(q = \text {O}\left( \log n\right) \), we give a faster and heuristic symplectic lattice reduction algorithm with approximation factor \(2^{\widetilde{\text {O}}\left( n\right) }\) in time:
where C is a bound on the condition number of the input matrix. For a power of two cyclotomic fields and large enough C, this complexity is a polynomial \(\widetilde{\text {O}}\left( n^{\log _2(3)}C\right) \).
Practical impacts in cryptography. Our reduction algorithms run in polynomial time and only achieve an exponential approximation factor. They can not be used per se to reevaluate the security parameters of NIST candidates, as their security estimates are based on better algorithms such as thedbkz [31]. However, using the symplectic structure, one can halve the complexity of this algorithmFootnote 1.
We test our algorithms on a large instance coming from multilinear map candidates based on ideal lattices [3] where \(q\approx 2^{6675}\) and \(N=2^{16}\). It can be solved over the smaller field \(n=2^{11}\) in 13 core-days. If we compare this computation with the previous large computation with fplll [44], Albrecht et al. were able to compute with \(n=2^8\), \(q\approx 2^{240}\) in 120 h. As the complexity of their code is about \(n^4\log (q)^2\) one can estimate an improvement factor of 4 million.
We improve the running time of the Gentry-Szydlo algorithm [14] using better ideal arithmetic. Instead of the classical \(\mathbf {Z}\)-basis representation, we represent ideals with a small family of generators over the order of a subfield of \({\mathbf {K}}\). The product of two ideals is the family of all products of generators. To make this work we need to sample a bit more than \([\mathbf {L}: \mathbf {K}]\) random elements in the product so that with overwhelming probability the ideal generated by these elements is the product ideal itself. As this increases the size of the family, we need fast lattice reductions to reduce the family as this operation is called many times. The overall complexity is \(\widetilde{\text {O}}\left( n^3\right) \), while previous implementation runs in \(\text {O}\left( n^6\right) \). The algorithm run in dimension 1024 in 103 h.
High-level description of the algorithms. The two algorithms leverage on the recursive strategy of Novocin et al. [37] to change the precisions at each level, of Albrecht et al. [2, 38] to descend recursively in smaller subfields using the relative norm functions, and the approach of Villard to make the algorithm parallel. The symplectic algorithm deeply extends the work of Gama et al. [11] by mixing it with the recursion strategy. Our theorems are stated for 2-dimensional lattices, but the algorithms run for lattices of dimension d. The reason is that even though we begin with a 2-by-2 matrix, after one recursion step, if the relative extension degree is 2, we get a 4-by-4 matrix. Consequently, we have to deal with more general dimensions. A more general theorem is claimed in [23]. Figure 1 is a flowchart of the different subroutines used in the algorithms.
A module over \(\mathbf {K}\) of rank d can be defined by a d-dimensional matrix M with coefficients in \(\mathcal {O}_{\mathbf {K}}\). If \(M\in (\mathcal {O}_{\mathbf {K}})^{d\times d}\) reducing M means finding a unimodular matrix \(U \in (\mathcal {O}_{\mathbf {K}})^{d\times d}\) such that MU has short and nearly orthogonal vectors in \((\mathcal {O}_{\mathbf {K}})^d\). Unimodular matrices in \((\mathcal {O}_{\mathbf {K}})^{d\times d}\) form a multiplicative group whose determinants are units in \(\mathcal {O}_{\mathbf {K}}\). It turns out that in such ring, the number of units is usually much higher than in \(\mathbf {Z}\) where we only have \(\pm 1\). One can define orthogonality of vectors using a positive quadratic form as a generalization of the usual scalar product on \(\mathbf {R}^d\), with vectors over \(\mathbf {C}\). There is two natural representations of elements for \(\alpha =\sum _i a_i\zeta ^i \in \mathcal {O}_{\mathbf {K}}\) with \(a_i\in \mathbf {Z}\). The most simple one is the representation by coefficients \((a_0,\ldots ,a_{n-1})\). The second representation is better in theory and is more convenient since it allows efficient computations: multiplication and addition can be achieved coefficient-wise. It sends \(\alpha \) to all its conjugates: the evaluations at all nth primitive roots of unity (\(\exp (2i\pi k/n)\) with \(\gcd (k,n)=1\)) of the polynomial \(\alpha (X)=a_0+a_1X+\ldots +a_{n-1}X^{n-1}\). Finally, it is possible to define a geometric norm on the representation by evaluations, a.k.a. embeddings, by extending the norm over \(\mathbf {C}\) to vectors. This norm induces a distance between elements of \(\mathcal {O}_{\mathbf {K}}\).
As said in [26], the major challenges for reducing algebraic lattices is that the algebraic norm and embedding norm does not always coincide for algebraic lattices, contrary to the Euclidean case. Some operations in lll require to work with the algebraic norm, when the volume of the lattice is involved, while when we have to take care of the size, we rely on a geometric norm, and unfortunately the algebraic norm is not a geometric norm.
Reduction of rank-n. This algorithm described in Sect. 3.8 is the main function of the algorithm and its goal is to reduce a lattice of rank \(d=n\) at the beginning. It is a recursive function that at the leaves of the recursion tree (2-dimensional lattice over \(\mathbf {Z}\)) calls Schönhage algorithm. The idea is to progressively change the basis making its profile flatter step-by-step during \(\rho \) iterations. The value \(\rho \) hence controls the overall complexity. In dimension d for a precision p, \(\rho \) is in \(O(d^2\log p)\). The precision is estimated by the size of the ratio between the largest and smallest embeddings of the Gram-Schmidt at each of the \(\rho \) iterations. The best value for \(\rho \) is estimated via a dynamical system analysis, sharing similarities with the one of [16]. Interestingly, the complexity equation reminds the heat equation in physics, whose diffusion characteristic time is quadratic in the space diameter.
A single iteration is organized in the same way as in (classical) lll pass on the whole basis: first, the Gram-Schmidt orthogonalization process is called, followed by a reduction in size of the Gram-Schmidt values. We call the first stage QR-decomposition as most modern lll versions implement this algorithm. The size-reduction algorithm allows us to keep the manipulated matrices well-conditioned. The whole lll process aimed at making the basis well-conditioned, i.e. making the ratio between the largest and smallest Gram-Schmidt vector as low as possible. The idea of lll consists of pushing the weight of the heaviest Gram-Schmidt to the lightest ones using Lagrange reduction step of 2-dimensional lattices.
Then, the main loop of lll is applied on the whole basis by splitting the base in 2-dimensional sublattices. This loop is orchestrated with odd-even steps à la Villard
[45] depending on the parity of the iteration. Instead of reducing the vectors \((b_i, b_{i+1})\) for \(i=1\) to \(n-1\) in lll which is inherently a sequential process, Villard proposed to reduce vectors \((b_{2i+1},b_{2i+2})\) for \(i=0\) to \(n/2\,-\,1\) in odd passes and \((b_{2i},b_{2i+1})\) for \(i=1\) to \(n/2-1\) in even passes. Consequently, at each pass all 2-dimensional sublattices \(\{(b_{2i+1},b_{2i+2})\}_i\) or \(\{(b_{2i},b_{2i+1})\}_i\) can be reduced in parallel. According to some condition on consecutive Gram-Schmidt norms (similar to Lovász condition), we recurse on smaller sublattices by first calling the
 algorithm and then the
algorithm and then the
 Algorithm in smaller dimension. Once we go back, we lift the unimodular matrix to the above subfield and apply it on the basis matrix. At the end of this algorithm, all unimodular matrices that have been computed during the \(\rho \) steps are multiplied together to obtain the global unimodular transformation.
Algorithm in smaller dimension. Once we go back, we lift the unimodular matrix to the above subfield and apply it on the basis matrix. At the end of this algorithm, all unimodular matrices that have been computed during the \(\rho \) steps are multiplied together to obtain the global unimodular transformation.
The main parameter is how we define a Lovász condition for algebraic lattices. It is crucial to control the approximation factor of our algorithms and the slope of the profile is named \(\alpha \), the approximation factor will be in \(2^{\alpha d}\). As previously mentioned, the goal is to transfer the weight of the first vector to the second one. Each iteration transforms consecutive Gram-Schmidt norms \(R_{i,i}\) and \(R_{i+1,i+1}\) to their average. The caveat of our algorithms is that the approximation factor will be higher than the one of lll because when we lift the solution, the vectors will be a little larger. We are however able to keep it exponential in \(\tilde{O}(n)\). As it depends on the number of subfields, this parameter will be different in the standard and symplectic algorithms. Indeed, in the symplectic algorithm, we cannot take any subfields and they have to be denser. Therefore, we recurse more and the approximation factor becomes higher.
QR-decomposition. This algorithm is described in Sect. 2.4 and computes the Gram-Schmidt decomposition. Since it uses purely algebraic operations, it is easy to adapt it for algebraic lattices once the hermitian product and norm are defined.
Size-reduce. This algorithm is given in Sect. 3.2 and its goal is to reduce the size of the vectors. When the field is \(\mathbf {Q}\) in the classical lll, we just round the coefficients to the nearest integer. Rounding in cyclotomic fields is not as easy as in \(\mathbf {Z}\) as the \(\mathcal {O}_{\mathbf {K}}\) lattice is less orthogonal. The idea is that we have to solve an approx-cvp instance in the \(\mathcal {O}_{\mathbf {K}}\)-lattice. In theory, we need to compute a unit close to \(R_{i,i}\) as in
[9] which is easy since the unit-log lattice is nearly orthogonal in the cyclotomic case. In practice, it is not needed and as it is reported in
[38], it works well without it. This operation will not change the algebraic norm of the elements, but make the embedding coefficients all of the same sizes, so that it helps to make the matrix well-conditioned and avoid a blow-up in the precision. It is also very important in the
 algorithm for controlling the size of the elements.
algorithm for controlling the size of the elements.
Reduction of rank-2 projected sublattices. The reduction of rank-2 projected sublattices first extracts 2 column vectors
and according to Lovász condition \(\mathcal {N}_{\mathbf {K}_h/\mathbf {Q}}(R_{i,i}) \leqslant 2^{2(1+\varepsilon )\alpha n_h^2} \mathcal {N}_{\mathbf {K}_h/\mathbf {Q}}(R_{i+1,i+1})\), it continues the descent. The recursion to smaller subfields is composed of the Descend and
 algorithm explained in Sect. 3.4 and is mainly depacking/packing values. Once the recursion terminates, it calls back the Lift algorithm.
algorithm explained in Sect. 3.4 and is mainly depacking/packing values. Once the recursion terminates, it calls back the Lift algorithm.
Lift and Generalized Euclidean Algorithm. This algorithm is described in Sect. 3.7. This operation requires to be careful otherwise the size of the lifted vectors will explode. The reduction at the bottom of the tree will return a short vector in the module. We need to complete this vector so that they both generate the same rank-2 module as the one given at the level of the recursion. The idea is to use a generalization of the extended Euclidean (
 algorithm in cyclotomic fields since we know that the determinant of the unimodal transformation has a determinant equal to 1. In the end, we size-reduce the basis to make vectors of the same size with balanced coefficients. We show that the operation works if we start with two elements a and b in a subfield \(\mathbf {K}_h\) so that their absolute norms \(\mathcal {N}_{\mathbf {K}_h/\mathbf {Q}}(a)\) and \(\mathcal {N}_{\mathbf {K}_h/\mathbf {Q}}(b)\) in \(\mathbf {Z}\) are coprime.
algorithm in cyclotomic fields since we know that the determinant of the unimodal transformation has a determinant equal to 1. In the end, we size-reduce the basis to make vectors of the same size with balanced coefficients. We show that the operation works if we start with two elements a and b in a subfield \(\mathbf {K}_h\) so that their absolute norms \(\mathcal {N}_{\mathbf {K}_h/\mathbf {Q}}(a)\) and \(\mathcal {N}_{\mathbf {K}_h/\mathbf {Q}}(b)\) in \(\mathbf {Z}\) are coprime.
The lift operation can fail in some instances as when we lift small elements, they do not always generate the whole rank-2 module. We work around this problem by lifting many small elements. In practice, this heuristic always works.
Symplectic Algorithm. The algorithm is the same as the standard algorithm but it changes the size-reduction which is presented in Sect. 4. It uses operations that maintain the symplecticity of the matrix. We used the symplectic reduction [11] at each step of the recursion. To do this, we need to show that it is possible to define the symplectic geometry in all subfields when we descend the tower field.
Comparison with other works. More recently some independent line of research started to tackle the problem of reduction of algebraic lattices [26, 32]. These papers give polynomial time reduction from \(\gamma \)-module-svp (or \(\gamma \)-Hermite-svp) in arbitrary rank to the same problem in small rank for all number fields. In particular in [26], for rank-2 modules, they present a \(\gamma \)-svp heuristic algorithm with approximation factor is \(2^{(\log d)^{O(1)}}\) in cyclotomic rings with quantum polynomial time given a cvp oracle that only depends on K in dimension more than \(d^2\). Consequently, an implementation would rely on an actual oracle for the latter problem with running time \(2^{d^2}\).
Organization of the paper. The next section is devoted to a succinct presentation of the mathematical objects required in the presentation of our framework. In Sect. 3 we introduce an algorithm which reduces rank-2 modules. Then, in Sect. 4, we explain how to leverage a natural symplectic structure to obtain an even faster reduction. We give implementation details in Sect. 5 and some cryptographic applications in Sect. 6.
2 Background
2.1 Computational Model and Notations
We use the word-ram model with unit cost and logarithmic size register (see for instance [30, Section 2.2]). An integer \(n\in \mathbf {Z}\) is said log-smooth if all its prime factors are bounded by \(\log (n)\). For a field \(\mathbf {K}\), let us denote by \(\mathbf {K}^{d\times d}\) the space of square matrices of size d over \(\mathbf {K}\), \(\text {GL}_d(\mathbf {K})\) its group of invertibles. Denote classically the elementary matrices by \(T_{i,j}(\lambda )\) and \(D_i(\lambda )\) for respectively the transvection (or shear mapping) and the dilatation of parameter \(\lambda \). We extend the definition of the product for any pair of matrices (A, B): for every matrix C with compatible size with A and B, we set: \((A,B)\cdot C = (AC,BC)\). We will denote the \(L_2\) norm of a vector \(x=(x_1,\ldots x_d)\) by \(\Vert x\Vert =\sqrt{\sum _i x_i^2}\) and the Frobenius norm of matrices by \(\Vert A\Vert _2=\sqrt{\sum _i \sum _j |A_{i,j}|^2}\) for a matrix \(A=(A_{i,j})\). The condition number \(\kappa (A)=\Vert A\Vert _2\Vert A^{-1}\Vert _2\), where A is a real or complex matrix and the norm used here is the spectral norm. We adopt the following conventions for submatrix extraction: for any matrix \(A = (A_{i,j})\in \mathbf {K}^{d\times d}\) and \(1\leqslant i<j\leqslant d, 1\leqslant k<\ell \leqslant d\), define the submatrix \(A[i:j,k:\ell ] = \left( A_{u,v}\right) _{i\leqslant u\leqslant j, k\leqslant v\leqslant \ell }\), while \(A_u\) refers to the u-th column of A.
2.2 Cyclotomic Fields and Modules over \(\mathbf {Z}[\zeta _f]\)
Background on Algebraic number theory can be found in Neukirch’s book [34]. Let \(\varPhi _f \in \mathbf {Z}[X]\) be the f-th cyclotomic polynomial, the unique monic polynomial whose roots \(\zeta _f^k=\exp (2ik\pi /f)\) with \(\gcd (k,f)=1\) are the f-th primitive roots of the unity. Therefore it can be written as \(\varPhi _f = \prod _{k\in \mathbf {Z}_f^{\times }} (X-\zeta _f^k)\) and the cyclotomic field \(\mathbf {Q}(\zeta _f)\) is obtained by adjoining a primitive root \(\zeta _f\) to the rational numbers. As such, \(\mathbf {Q}(\zeta _f)\) is isomorphic to the field \(\mathbf {Q}[X]/(\varPhi _f)\). Its degree over \(\mathbf {Q}\) is \(\mathrm {deg} \ (\varPhi _f) = \varphi (f)\), the Euler totient of f. In this specific class of number fields, the ring of integers is precisely \(\mathbf {Z}[X]/(\varPhi _f) \cong \mathbf {Z}[\zeta _f]\) (see [34, Prop. 10.2]).
Canonical Hermitian structure. Let \(\mathcal {M}\) be a free module of rank d over the cyclotomic ring of integers \(\mathbf {Z}[\zeta _f]\). It is isomorphic to \(\bigoplus _{i=1}^d \alpha _i \mathbf {Z}[\zeta _f]\), for some linearly independent vectors \(\alpha _i = (\alpha _i^{(1)}, \ldots , \alpha _i^{(d)}) \in \mathbf {Q}(\zeta _f)^d\). The Hermitian structure of \(\mathbf {Q}(\zeta _f)^d\) lifts to \(\mathcal {M}{}\) as defined by  on the basis elements and extended by (bi)linearity. We denote by \(\Vert \cdot \Vert \) the corresponding norm. We use the same notation to denote the associated induced norm on endomorphisms (or associated matrices) over the vector space \(\mathbf {Q}(\zeta _f)^d\).
on the basis elements and extended by (bi)linearity. We denote by \(\Vert \cdot \Vert \) the corresponding norm. We use the same notation to denote the associated induced norm on endomorphisms (or associated matrices) over the vector space \(\mathbf {Q}(\zeta _f)^d\).
Relative structure of the ring of integers in a tower. Let \(\mathbf {K}\subseteq \mathbf {L}\) be a cyclotomic subfield of \(\mathbf {L}\) of index n. Then \(\mathcal {O}_{\mathbf {K}}\) is a subring of \(\mathcal {O}_\mathbf {L}\), so that \(\mathcal {O}_\mathbf {L}\) is a free module over \(\mathcal {O}_{\mathbf {K}}\)Footnote 2. Henceforth, the module \(\mathcal {M}\) can itself be viewed as a free module over \(\mathcal {O}_\mathbf {K}\) of rank dn. Indeed, consider \((\xi _1, \ldots , \xi _n)\) a basis of \(\mathcal {O}_\mathbf {K}\) over \(\mathcal {O}_{\mathbf {L}}\) and \((v_1, \ldots , v_d)\) a basis of \(\mathcal {M}\) over \(\mathcal {O}_\mathbf {K}\). For any \(1\leqslant i\leqslant d\), each coefficient of the vector \(v_i\) decomposes uniquely in the basis \((\xi _j)\). Grouping the corresponding coefficients yields a decomposition \(v_i = v_i^{(1)}\xi _1 + \cdots + v_i^{(n)} \xi _n\), where \(v_i^{(j)}\in \mathcal {O}_{\mathbf {L}}^{dn}\). The family \(\left( v_i^{(j)}\xi _j\right) _{1\leqslant i \leqslant d, 1\leqslant j\leqslant n}\) is a basis of \(\mathcal {M}\) viewed as \(\mathcal {O}_\mathbf {K}\)-module.
2.3 Unit Rounding in Cyclotomic Fields
The group of units of a number field is the group of invertible elements of its ring of integers. Giving the complete description of the units of a generic number field is a computationally hard problem in algorithmic number theory. However, in cyclotomic fields, it is possible to describe a subgroup of finite index of the unit group, called the cyclotomic units. This subgroup contains all the units that are products of elements of the form \(\zeta _f^i - 1\) for any \(1\leqslant i\leqslant f\). As these units are dense, structured and explicit we can use them to round an element. The following theorem is a quasilinear variant of the result of
[9, Theorem 6.3] which is proved in
[23] and
 is the corresponding algorithm.
is the corresponding algorithm.
Theorem 1
Let \(\mathbf {K}\) be the cyclotomic field of conductor f. There is a quasi-linear time randomized algorithm that given any element in \(x\in (\mathbf {R}\otimes \mathbf {K})^\times \) finds a unit \(u\in \mathcal {O}_\mathbf {K}^\times \) such that for any field embedding \(\sigma :\mathbf {K}\rightarrow \mathbf {C}\) we have
Remark 1
Since \(\frac{f}{\varphi (f)}=\text {O}\left( \log \log f\right) \) and \(n=\varphi (f)\) the absolute degree of \(\mathbf {K}\), the bound in Theorem 1 becomes \(2^{\text {O}\left( \sqrt{n\log n\log \log n}\right) }\mathcal {N}_{\mathbf {K}/\mathbf {Q}}(x)^{\frac{1}{n}}\).
2.4 \(\mathcal {O}_\mathbf {K}\)-lattices
We now generalize the notion of Euclidean lattice to the higher-degree context. Recall that a Euclidean lattice is a finitely generated free \(\mathbf {Z}\)-module \(\varLambda \) endowed with a Euclidean structure on its real ambient space \(\varLambda \otimes _\mathbf {Z}\mathbf {R}\). To extend this definition we replace the base-ring \(\mathbf {Z}\) by the ring of integer \(\mathcal {O}_\mathbf {K}\) of a number field \(\mathbf {K}\). In the present context, we will keep the freeness condition of the module, even if this setting is slightly too restrictive in general number fields.
Definition 1
(\(\mathcal {O}_\mathbf {K}\)-lattice). Let \(\mathbf {K}\) be a cyclotomic field. An \(\mathcal {O}_\mathbf {K}\)-lattice—or algebraic lattice over \(\mathcal {O}_\mathbf {K}\)—is a free \(\mathcal {O}_\mathbf {K}\)-module \(\varLambda \) endowed with a \(\mathbf {K}\otimes \mathbf {R}\)-linear positive definite self-adjoint form on the ambient vector space \(\varLambda \otimes _{\mathcal {O}_\mathbf {K}} \mathbf {R}\).
Orthogonalization process. Taking the basis \((m_1, \ldots , m_d)\) of \(\mathcal {M}\), one can construct an orthogonal family \((m_1^*, \ldots , m_d^*)\) such that the flag of subspaces \((\oplus _{i=1}^k b_i\mathbf {K})_{1\leqslant k\leqslant d}\) is preserved. This routine is exactly the same as for Euclidean lattices and is given in Algorithm 1,
 . We present it here in its matrix form, which generalizes to \(\text {GL}_d(\mathbf {K}\otimes \mathbf {R})\) QR-decomposition in \(\text {GL}_d(\mathbf {R})\). The volume of \(\mathcal {M}\) can be computed from the norms of the Gram-Schmidt stored in the matrix R as: \(\mathrm {vol} \ \left( {\mathcal {M}}\right) = \mathcal {N}_{\mathbf {K}/\mathbf {Q}}\left( \prod _{i=1}^d R_{i,i}\right) \), while over \(\mathbf {Z}\), it is \(\prod _{i=1}^d R_{i,i}\).
. We present it here in its matrix form, which generalizes to \(\text {GL}_d(\mathbf {K}\otimes \mathbf {R})\) QR-decomposition in \(\text {GL}_d(\mathbf {R})\). The volume of \(\mathcal {M}\) can be computed from the norms of the Gram-Schmidt stored in the matrix R as: \(\mathrm {vol} \ \left( {\mathcal {M}}\right) = \mathcal {N}_{\mathbf {K}/\mathbf {Q}}\left( \prod _{i=1}^d R_{i,i}\right) \), while over \(\mathbf {Z}\), it is \(\prod _{i=1}^d R_{i,i}\).

3 Reduction of \(\mathcal {O}_\mathbf {K}\)-Modules in Cyclotomic Fields
We describe now our first reduction for lattices over cyclotomic fields. Let h be a non-negative integer, a tower of log-smooth conductor cyclotomic fields
and \(1 = n_0< n_1< \cdots < n_h\) their respective degrees over \(\mathbf {Q}\). Then, we consider a free module \(\mathcal {M}\) of rank d over the upper field \(\mathbf {K}_h\), which is represented by a basis \((m_1, \ldots , m_d)\) given as the columns of a matrix \(M\in \mathcal {O}_{\mathbf {K}_h}^{d\times d}\). We denote by \(\langle a,b\rangle \) the \(\mathcal {O}_{\mathbf {K}_h}\)-module \(a\mathcal {O}_{\mathbf {K}_h}\oplus b\mathcal {O}_{\mathbf {K}_h}\). The reduction algorithm returns a unimodular transformation such that the basis
 has a small first vector.
has a small first vector.
3.1 Outer Iteration
To reduce the module \(\mathcal {M}\) we adopt an iterative strategy to progressively modify the basis. For \(\rho \) steps, a reduction pass over the current basis is performed, with \(\rho \) being a parameter whose value is computed to optimizeFootnote 3 the complexity of the whole algorithm while still ensuring the reduceness of the basis. As in the lll algorithm a size-reduction operation is conducted to control the size of the coefficients of the basis and ensure that the running time of the reduction remains polynomial. Note that for number fields this subroutine is adapted to deal with units of \(\mathcal {O}_{\mathbf {K}_h}\) when rounding. In a word, we make use of the numerous units of this field to shrink the discrepancy of the embeddings of the coefficients of the basis. This allows computation with less precision.
3.2 Unit-size-reduction for \(\mathcal {O}_{\mathbf {K}_h}\)-Modules
As indicated, in order to adapt the size-reduction process to the module setting, one needs to adjust the rounding function. When \(\mathbf {K}_h=\mathbf {Q}\), the rounding boils down to finding the closest element in \(\mathcal {O}_\mathbf {K}=\mathbf {Z}\), which is encompassed by the round function \(\lceil \cdot \rfloor \). In the higher-dimensional context, we need to approximate any element of \(\mathbf {K}_h\) by a close element of \(\mathcal {O}_{\mathbf {K}_h}\).

Note that finding the closest integral element is not efficiently doable. The naive approach consists of reducing the problem to the resolution of the closest integer problem in the Euclidean lattice of rank \(n_h\) given by \(\mathcal {O}_{\mathbf {K}_h}\) under the embedding.
Nonetheless, finding a target vector close enough to the target suffices for our application. We simply define the rounding of an element \(\alpha \in \mathbf {K}_h\) as the integral rounding on its coefficients when represented in the power base of \(\mathbf {K}_h\).
We add here an important and necessary modification to the size-reduction algorithm: before the actual size-reduction occurred, we compute a unit u using Theorem 1 close to \(R_{i,i}\). The vector \(M_i\) is then divided by u. While not changing the algebraic norms of the elements, this technicality forces the embeddings of the coefficients to be balanced and helps the reduced matrix to be well-conditioned. This avoids a blow-up of the precision required during the computation. This modified size-reduction is fully described in Algorithm 2,
 (the two technical modifications to the usual size-reduction are encompassed at line 3 for the reconditioning using the unit rounding and at line 7 where the approximate rounding is performed coefficient-wise).
(the two technical modifications to the usual size-reduction are encompassed at line 3 for the reconditioning using the unit rounding and at line 7 where the approximate rounding is performed coefficient-wise).
3.3 Step Reduction Subroutine
We now take a look at the step reduction pass, once the size-reduction has occurred. The lll algorithm reduces to the treatment of rank-2 modules and more precisely to iteratively reduce orthogonally projected rank-2 modules. We use the same idea and the step reduction pass over the current basis is a sequence of reductions of projected rank 2 \(\mathcal {O}_{\mathbf {K}_h}-\)modules. However on the contrary to the lll algorithm, we do not proceed progressively along the basis, but instead, reduce \(\lfloor d/2\rfloor \) independent rank 2 modules at each step. This design enables an efficient parallel implementation which reduces submodules simultaneously, in the same way that the classical lll algorithm can be parallelized [17, 45].
Formally, given the basis of \(\mathcal {M}\) collected in the matrix M, let us decompose it as \(M=QR\) with Q orthogonal and R upper triangular. For \(1\leqslant i\leqslant d-1\), denote by \(r_i\) the vector \(\left( R_{i,i}, R_{i+1,i}=0\right) \), and \(r'_{i}\) the vector \(\left( R_{i,i+1}, R_{i+1,i+1}\right) \). The module \(\mathcal {R}_{i}\) spanned by the vectors \(r_i\) and \(r'_i\) encodes exactly the projection of \(\mathcal {M}_i = \big \langle m_{i-1}, m_{i} \big \rangle \) over the orthogonal space to the first \(i-1\) vectors \((m_1, \ldots , m_{i-1})\). In order to recursively call the reduction algorithm on \(\mathcal {R}_i\) we need to descend it to the subfield \(\mathbf {K}_{h-1}\) first. This means seeing this \(\mathcal {O}_{\mathbf {K}_h}\)-module of rank 2 as an \(\mathcal {O}_{\mathbf {K}_{h-1}}\)-module of rank \(2[\mathbf {K}_h:\mathbf {K}_{h-1}]\).
3.4 Interlude: Descending to Cyclotomic Subfields
Remark now that since \(\mathbf {K}_h\) is a cyclotomic extension of the cyclotomic field \(\mathbf {K}_{h-1}\), there exists a root of unity \(\zeta \) such that \( \mathcal {O}_{\mathbf {K}_h} = \mathcal {O}_{\mathbf {K}_{h-1}} \oplus \zeta \mathcal {O}_{\mathbf {K}_{h-1}} \oplus \cdots \oplus \zeta ^{q_h-1} \mathcal {O}_{\mathbf {K}_{h-1}},\) for \(q_h=n_h/n_{h-1}\) being the relative degree of \(\mathbf {K}_h\) over \(\mathbf {K}_{h-1}\). As a consequence, the module \(\mathcal {R}_i\) decomposes over \(\mathcal {O}_{\mathbf {K}_{h-1}}\) as:
yielding a basis of \(\mathcal {R}_i\) viewed as a free \(\mathcal {O}_{\mathbf {K}_{h-1}}\)-module of rank \(2\times q_h\). This module can then be recursively reduced, this time over a tower of height \(h-1\). This conversion from an \(\mathcal {O}_{\mathbf {K}_h}-\)module to an \(\mathcal {O}_{\mathbf {K}_{h-1}}-\) module is referred as the function
 . Conversely, any vector \(u\in \mathcal {O}_{\mathbf {K}_{h-1}}^{2q_h}\) can be seen with this decomposition as a vector of \(\mathcal {O}_{\mathbf {K}_h}^2\) by grouping the coefficients as
. Conversely, any vector \(u\in \mathcal {O}_{\mathbf {K}_{h-1}}^{2q_h}\) can be seen with this decomposition as a vector of \(\mathcal {O}_{\mathbf {K}_h}^2\) by grouping the coefficients as
We denote by
 this conversion.
this conversion.
3.5 Back on the Step Reduction
We start by reducing (with a recursive call after descending) all \(\mathcal {O}_{\mathbf {K}_{h-1}}\)-modules \(\mathcal {R}_{2i} = \big \langle r_{2i-1}, r'_{2i} \big \rangle \) for \(1\leqslant i \leqslant \lfloor d/2 \rfloor \). By specification, each of these reductions allows to find a small element of the \(\mathcal {O}_{\mathbf {K}_h}\)-submodule \(\mathcal {M}_{2i} = \big \langle m_{2i-1}, m_{2i} \big \rangle \) which is then completedFootnote 4 in a basis of \(\mathcal {M}_{2i}\). But on the contrary to the classical lll reduction, this sequence of pairwise independent reductions does not mix the elements \(m_{2i}\) and \(m_{2i+1}\), in the sense that no reduction of the module projected from \(\langle m_{2i}, m_{2i+1}\rangle \) is performed. To do so, we then perform the same sequence of pairwise reductions but with all indices shifted by 1: we reduce the planes \(\big \langle r_{2i}, r'_{2i+1} \big \rangle \) for each \(1\leqslant i \leqslant \lfloor d/2 \rfloor \), as depicted in Fig. 2.
3.6 Reduction of the Leaves
As the recursive calls descend along the tower of number fields, the bottom of the recursion tree requires reducing \(\mathcal {O}_{\mathbf {K}_0} (= \mathcal {O}_\mathbf {Q}= \mathbf {Z})\)-modules, that is, Euclidean lattices. As a consequence, the step reduction performs calls to a reduction oracle for plane Euclidean lattices. For the sake of efficiency we adapt Schönhage’s algorithm
[42] to reduce these lattices, which is faster than the traditional Gauss’ reduction. This algorithm is an extension to the bidimensional case of the half-GCD algorithm, in the same way, that Gauss’ algorithm can be seen as a bidimensional generalization of the classical GCD computation. The original algorithm of Schönhage only deals with the reduction of binary quadratic forms, but can be straightforwardly adapted to reduce rank 2 Euclidean lattices, and to return the corresponding unimodular transformation matrix. In all of the following, we denote by
 this modified procedure.
this modified procedure.
3.7 The Lifting Phase
At this point, we recursively called the reduction procedure to reduce the descent of projected modules of rank 2 of the form \(\mathcal {R}_i = \langle r_i, r'_{i+1}\rangle \), over \(\mathbf {K}_{h-1}\). This yields a unimodular transformation \(U'\in \mathcal {O}_{\mathbf {K}_{h-1}}^{2q_h\times 2q_h}\) where \(q_h\) is the relative degree of \(\mathbf {K}_h\) over \(\mathbf {K}_{h-1}\). We now need to find a reduced basis of this projected sublattice over \(\mathcal {O}_{\mathbf {K}_h}\), so that we can apply the corresponding transformation on \(m_i\mathcal {O}_{\mathbf {K}_h}\oplus m_{i+1}\mathcal {O}_{\mathbf {K}_h}\) (like in the classical lll algorithm).
From \(U'\), we can find random short elements in the module (over \(\mathbf {K}_{h-1}\)) by computing a small linear combination of its first columns. By applying
 on one of them, we deduce some short \(x=a\cdot m_i+b\cdot m_{i+1}\). But then to replace \(m_i\) by x in the current basis, we need to complete this vector into a basis (x, y) of \(\mathcal {M}_i\) over \(\mathcal {O}_{\mathbf {K}_h}\). Saying differently, we want to complete a vector of \(\mathcal {O}_{\mathbf {K}_h}^2\) into a unimodular transformation. Indeed, suppose that such a vector y is found and denote by (v, u) its coordinates in the basis \((m_i, m_{i+1})\). By preservation of the volume we have:
on one of them, we deduce some short \(x=a\cdot m_i+b\cdot m_{i+1}\). But then to replace \(m_i\) by x in the current basis, we need to complete this vector into a basis (x, y) of \(\mathcal {M}_i\) over \(\mathcal {O}_{\mathbf {K}_h}\). Saying differently, we want to complete a vector of \(\mathcal {O}_{\mathbf {K}_h}^2\) into a unimodular transformation. Indeed, suppose that such a vector y is found and denote by (v, u) its coordinates in the basis \((m_i, m_{i+1})\). By preservation of the volume we have:
Therefore, finding the element y to complete x reduces to solving the Bézout equation in the unknown u and v \(au - bv = 1\) over the ring \(\mathcal {O}_{\mathbf {K}_h}\). Since this ring is in general not Euclidean we can not apply directly the Euclidean algorithm to solve this equation using the extended gcd algorithm. However, we can use the algebraic structure of the tower \(\mathbf {K}_h^\uparrow \) to recursively reduce the problem to the rational integers. This generalized Euclidean algorithm works as follows:
-
If \(\mathbf {K}_h = \mathbf {Q}\): The problem is then an instance of extended GCD search, which can be solved efficiently by the binary-GCD algorithm.
-
If the tower \(\mathbf {K}_h^\uparrow \) is not trivial: We make use of the structure of \(\mathbf {K}_h^\uparrow \) and first descend the problem to the subfield \(\mathbf {K}_{h-1}\) by applying the relative norm \(\mathcal {N}_{\mathbf {K}_h/\mathbf {K}_{h-1}}\): then, by recursive call on \(\mathcal {N}_{\mathbf {K}_h/\mathbf {K}_{h-1}}(a)\) and \(\mathcal {N}_{\mathbf {K}_h/\mathbf {K}_{h-1}}(b)\), we find two algebraic integers \(\mu \) and \(\nu \) of \(\mathcal {O}_{\mathbf {K}_{h-1}}\) fulfilling the equation:
$$\begin{aligned} \mu \mathcal {N}_{\mathbf {K}_h/\mathbf {K}_{h-1}}(a)-\nu \mathcal {N}_{\mathbf {K}_h/\mathbf {K}_{h-1}}(b) = 1. \end{aligned}$$(1)But now remark that for any element \(\alpha \in \mathcal {O}_{\mathbf {K}_h}\) we have, using the comatrix formula and the definition of the norm as a determinant that: \(\mathcal {N}_{\mathbf {K}_h/\mathbf {K}_{h-1}}(\alpha )\in \alpha \mathcal {O}_{\mathbf {K}_h}\), so that \(\alpha ^{-1}\mathcal {N}_{\mathbf {K}_h/\mathbf {K}_{h-1}}(\alpha )\in \mathcal {O}_{\mathbf {K}_h}\). Then, from Eq. (1):

-
Reduction of the size of solutions: The elements u, v found by the algorithm are not necessarily the smallest possible elements satisfying the Bézout equation. To avoid a blow-up in the size of the coefficients lifted, we do need to control the size of the solution at each step. Since the function
 preserves the determinant by construction and reduces the norm of the coefficients, we can use it to reduce the bitsize of u, v to (roughly) the bitsize of a and b.
preserves the determinant by construction and reduces the norm of the coefficients, we can use it to reduce the bitsize of u, v to (roughly) the bitsize of a and b.
The translation of this method is given in Algorithm 3,
 . The number of bits needed to represent the relative norms does not depend on the subfield, and the size-reduction forces the output vector to have the same bitsize as the input one. This is the main idea of the quasilinearity of the
. The number of bits needed to represent the relative norms does not depend on the subfield, and the size-reduction forces the output vector to have the same bitsize as the input one. This is the main idea of the quasilinearity of the
 algorithm. The algorithm needs \(\mathcal {N}_{\mathbf {K}_h/\mathbf {Q}}(a)\) to be prime with \(\mathcal {N}_{\mathbf {K}_h/\mathbf {Q}}(b)\). We assume that we can always find quickly such a, b with a short x. This will lead to Heuristic 1, and its validity is discussed in Sect. 5.4.
algorithm. The algorithm needs \(\mathcal {N}_{\mathbf {K}_h/\mathbf {Q}}(a)\) to be prime with \(\mathcal {N}_{\mathbf {K}_h/\mathbf {Q}}(b)\). We assume that we can always find quickly such a, b with a short x. This will lead to Heuristic 1, and its validity is discussed in Sect. 5.4.


Remark 2
This algorithm is related to the one proposed in
[38]. However, the claimed complexity of their algorithm is incorrect, as the size of the lifted solutions can not be controlled. This problem is resolved here by using the quasi-linear
 rounding algorithm. More generally the unit rounding is in a lll-type algorithm, at least theoretically, mandatory. In particular, a swap when the basis is not reduced with the definition in
[21] may not lead to a reduction in potential so that the proof of
[21, Theorem 3] is incorrect. We also point out that without a bound on the unit contributions, we have no polynomial bound on the number of bits used in their Algorithm 3. From a practical point of view, it does not seem to be a problem. If this is the case, our algorithm can be used every time we have a reasonable tower of number fields.
rounding algorithm. More generally the unit rounding is in a lll-type algorithm, at least theoretically, mandatory. In particular, a swap when the basis is not reduced with the definition in
[21] may not lead to a reduction in potential so that the proof of
[21, Theorem 3] is incorrect. We also point out that without a bound on the unit contributions, we have no polynomial bound on the number of bits used in their Algorithm 3. From a practical point of view, it does not seem to be a problem. If this is the case, our algorithm can be used every time we have a reasonable tower of number fields.
3.8 Wrapping-Up and Complexity
The lattice reduction algorithm is described in Algorithm 4. It is parametrized by two variables \(\varepsilon \) and \(\alpha \), which are related to the approximation factor of the reduction. The precise values of these constants depend on the conductor of the upper field. A more complete outline of the reduction is given in [23].
To express our complexity result, we introduce a mild heuristic, which claims that the size of the elements obtained after the
 function is not too large.
function is not too large.
Heuristic 1
(Size of lifting). Denote by \(R^{(i)}\) the R-part of the QR decomposition of the basis at the i-th step of the algorithm
 . For any \(1\leqslant i\leqslant \rho \) and any \(1\leqslant j \leqslant d\) where a call to
. For any \(1\leqslant i\leqslant \rho \) and any \(1\leqslant j \leqslant d\) where a call to
 happened:
happened:
A discussion on the validity of this heuristic is done in Sect. 5.4.
Claim 1
Let f be a log-smooth integer. Under Heuristic 1, the complexity of Algorithm
 on rank 2-modules over \(\mathbf {K}=\mathbf {Q}[x]/\varPhi _f(x)\), represented as a matrix M whose number of bits in the input coefficients is uniformly bounded by \(B>n\), is heuristically a \(\widetilde{\text {O}}\left( n^2B\right) \) with \(n=\varphi (f)\). The first column of the reduced matrix has its coefficients uniformly bounded by \(2^{\widetilde{\text {O}}\left( n\right) }\left( \mathrm {vol} \ M\right) ^{\frac{1}{2n}}\).
on rank 2-modules over \(\mathbf {K}=\mathbf {Q}[x]/\varPhi _f(x)\), represented as a matrix M whose number of bits in the input coefficients is uniformly bounded by \(B>n\), is heuristically a \(\widetilde{\text {O}}\left( n^2B\right) \) with \(n=\varphi (f)\). The first column of the reduced matrix has its coefficients uniformly bounded by \(2^{\widetilde{\text {O}}\left( n\right) }\left( \mathrm {vol} \ M\right) ^{\frac{1}{2n}}\).
A more technical analysis is given in
[23] and we present here the basic steps. First, remark that the input matrix can always be reconditioned using
 in time \(\widetilde{\text {O}}\left( n^2B\right) \) so that we might always suppose that its condition number is smaller than \(2^B\). We start by estimating the approximation factor of the reduction and deduce a bound in \(\text {O}\left( d^2\log p\right) \) on the number of rounds \(\rho \) required to achieve the reduction of the module \(\mathcal {M}\), where p is the precision needed to handle the full computation. We then prove that the limiting factor for the precision has to be large enough to represent the shortest embedding of the norm of the Gram-Schmidt orthogonalization of the initial basis. After that, we devise a bound by looking at the sum of all the bit sizes used in the recursive calls and conclude on the complexity. The critical part of the proof is to use the potential to show that dividing the degrees by \(\frac{d}{2}\) leads to a multiplication by a factor at most in \(\text {O}\left( d^2\right) \) of the sum of all the precisions in the recursive calls, instead of the obvious \(\text {O}\left( d^3\log p\right) \). This discrepancy in the number of bits actually needed by the reduction compared with the obvious bound allows to reduce at sufficiently low precision to diminish the overall complexity.
in time \(\widetilde{\text {O}}\left( n^2B\right) \) so that we might always suppose that its condition number is smaller than \(2^B\). We start by estimating the approximation factor of the reduction and deduce a bound in \(\text {O}\left( d^2\log p\right) \) on the number of rounds \(\rho \) required to achieve the reduction of the module \(\mathcal {M}\), where p is the precision needed to handle the full computation. We then prove that the limiting factor for the precision has to be large enough to represent the shortest embedding of the norm of the Gram-Schmidt orthogonalization of the initial basis. After that, we devise a bound by looking at the sum of all the bit sizes used in the recursive calls and conclude on the complexity. The critical part of the proof is to use the potential to show that dividing the degrees by \(\frac{d}{2}\) leads to a multiplication by a factor at most in \(\text {O}\left( d^2\right) \) of the sum of all the precisions in the recursive calls, instead of the obvious \(\text {O}\left( d^3\log p\right) \). This discrepancy in the number of bits actually needed by the reduction compared with the obvious bound allows to reduce at sufficiently low precision to diminish the overall complexity.
4 Symplectic Reduction
Here we demonstrate how to generate additional structure which is compatible the tower of number fields and how to exploit it to speed-up the size-reduction procedure of our algorithm, at every level of the recursion. This additional structure is in substance a generalization of the so-called symplectic group to tower of fields, which gives additional symmetries to lattices. In a word, we design a size-reduction which is compatible with this symplectic group, in the sense that it allows to perform the computation with only the first part of the basis and get the rest of the reduction for free, using these symmetries.
This technique can be thought as an algebraic generalization of the work [11] of Gama, Howgrave-Graham and Nguyen on lll-reduction for ntru lattices. In particular, we demonstrate that such techniques can be used for all towers of number fields. Where [11] gains a factor 2 for the reduction of structured lattices over \(\mathbf {Z}\), we gain a factor 2 at each level of the recursive calls of the reduction, which combines into an overall polynomial factor improvement.
After introducing the symplectic group and Darboux bases, we show how to generalize these constructions to tower of fields. Then we show that this tower of symplectic groups is compatible with the descent we use to recurse (namely the descent of a symplectic lattice over a subfield has to remain symplectic). Eventually, we the show that we can replace the
 sub-procedure by a tailored one for symplectic lattices.
sub-procedure by a tailored one for symplectic lattices.
4.1 On Symplectic Spaces and Symplectic Groups
We now briefly introduce the linear aspects of symplectic geometry and establish the parallel between the Euclidean and Symplectic spaces.
Definitions. A symplectic space is a finite dimensional vector space E endowed with an antisymmetric bilinear form \(J: E\times E\rightarrow E\). We can define a natural orthogonality relation between vectors \(x,y\in E\) as being \(J(x,y)=0\). The linear transformations of E letting the symplectic structure J invariant is a group, called the J-symplectic group(or symplectic group if the context makes J clear). This group plays a role similar to the orthogonal group for Euclidean spaces.
Darboux bases. Contrary to Euclidean spaces, a symplectic space does not possess an orthogonal basis, but instead a basis \(e_1, \ldots , e_d, f_1, \ldots , f_d\), so that for any indices \(i < j\) we have \(J(e_i, e_j) = 0, J(f_i, f_j) = 0, J(e_i, f_j) = 0 \) and \(J(e_i, f_i) = -J(f_i, e_i) > 0\), called a Darboux base. It implies in particular that any symplectic space has even dimension. Recall that by Gram-Schmidt orthogonalization, we can transform any basis of a Euclidean space in an orthogonal basis. This construction can be adapted to the symplectic case, to construct a Darboux base iteratively.
Symplectic lattice, size reduction. Given a lattice \(\varLambda \) and a symplectic form J, we say that \(\varLambda \) is J-symplectic if the matrix representing \(\varLambda \) let invariant the form J (as a comparison, if J was an inner product form, a lattice \(\varLambda \) preserving J would be represented with an orthonormal basis).
As mentioned in Sect. 3.2, an important tool to reduce lattices is the size-reduction procedure, which can be viewed as a discretization of the Gram-Schmidt orthogonalization. It aims at reducing the bitsize and the condition number of the lattice basis. When dealing with symplectic lattices, we can also discretize the process to obtain a basis which can be seen as a discretization of a Darboux basis. Using this process instead of the classical size-reduction would retrieve the situation of [11].
As we generalized the lattice formalism to \(\mathcal {O}_\mathbf {K}\)-modules in number fields, we now generalize the notions of symplectic lattices to the algebraic context.
4.2 J-Symplectic Group and Compatibility with Extensions
In all the following, we fix an arbitrary tower of number fields
For any \(1\leqslant i \leqslant h\) we denote by \(q_h\) the relative degree of \(\mathbf {K}_{h}\) over \(\mathbf {K}_{h-1}\). On any of these number fields, we can define a simple symplectic form, which derives from the determinant form.
Definition 2
Let \(\mathbf {K}\) be a field, and set J to be an antisymmetric bilinear form on \(\mathbf {K}^2\). A matrix \(M\in \mathbf {K}^{2\times 2}\) is said to be J-symplectic (or simply symplectic) if it lets the form J invariant, that is if \(J\circ M=J\).
Let us instantiate this definition in one of the fields of the tower \(\mathbf {K}_h^\uparrow \) on the \(2\times 2\)-determinant form. Let \(J_{h}\) be the antisymmetric bilinear form on \(\mathbf {K}_h^2\) which is given as the determinant of \(2\times 2\) matrices in \(\mathbf {K}_h\), i.e.
Remark 3
In the presented case, M is \(J_{h}\)-symplectic iff \(\det M=1\). Hence, we can always scale a basis so that this condition is verified.
At this point we have introduced a symplectic structure on \(\mathbf {K}_h\). But we want to have a symplectic structure at every level of the tower, so that we can use this structure at every level of the recursion when reducing a module. To do so, we need that the descent of a symplectic lattice over \(\mathbf {K}_h\) is also a symplectic lattice over all of these subfields. Formally, this corresponds to finding a form compatible with the descent of a symplectic matrix to \(\mathbf {K}_{h-1}\). Hence, we want to construct a form \(J_h'\) over \(\mathbf {K}_{h-1}\), such that the following lemma is true.
Lemma 1
Let M be a \(2\times 2\) matrix over \(\mathbf {K}_h\) which is \(J_{h}\)-symplectic, then its descent \(M'\in \mathbf {K}_{h-1}^{2q_h\times 2q_h}\) is \(J_{h}'\)-symplectic.
To do so, we descend the form \(J_{h}\) to \(\mathbf {K}_{h-1}\) by composition with a carefully constructed linear form \(\mathbf {K}_h \rightarrow \mathbf {K}_{h-1}\). We then extend the definition of symplectism to \(\mathbf {K}_{h-1}^{2q_h}\) by stating that a \(2q_h\times 2q_h\) matrix \(M'\) is symplectic if it preserves the \(J_{h}'\) form, that is if \(J'_h \circ M'=J'_h\).
But as the reduction is going, the current basis is subjected to transformations. In order to be able to continue to use the symmetries induced by the symplectism we need to ensure that the basis remains symplectic at every moment of the reduction. By induction, this boils down to show that every elementary transformations done by our algorithm
 preserves the symplectic structure.
preserves the symplectic structure.
4.3 Module Transformations Compatible With J-Symplectism
We treat here the slightly simpler case of Kummer-like extensions, which is the case we implemented in our proof-of-concept, as it encompasses the cryptographic cases. The general case is covered in the full version of this paper [23].
 We define \(R_{q_h}\) as the reverse diagonal of 1 in a square matrix of dimension \(q_h\). We use the notation \(A^s\) as a shorthand for \(R_{q_h}A^TR_{q_h}\), which corresponds to the reflection across the antidiagonal, that is exchanging the coefficients \(A_{i,j}\) with \(A_{q_h+1-i, q_h+1-j}\). We adapt here the work of Sawyer
[40].
We define \(R_{q_h}\) as the reverse diagonal of 1 in a square matrix of dimension \(q_h\). We use the notation \(A^s\) as a shorthand for \(R_{q_h}A^TR_{q_h}\), which corresponds to the reflection across the antidiagonal, that is exchanging the coefficients \(A_{i,j}\) with \(A_{q_h+1-i, q_h+1-j}\). We adapt here the work of Sawyer
[40].
Suppose that the defining polynomial of \(\mathbf {K}_h/\mathbf {K}_{h-1}\) is \(X^{q_h}+a\). Recall that \(J_{h}\) is the \(2\times 2\)-determinant form over \(\mathbf {K}_h^2\). We can compose it by the linear form

to obtain the matrix \(J'_{h}\), which becomes \(J_{h}' = \begin{pmatrix} 0 &{} R_{q_h} \\ -R_{q_h} &{} 0\end{pmatrix}\) in the power basis.
Lemma 2
Fix a basis of the symplectic space where the matrix corresponding to \(J'_h\) is \(\begin{pmatrix} 0 &{} R_{q_h} \\ -R_{q_h} &{} 0\end{pmatrix}\). For any M a \(J'_h\)-symplectic matrix and its QR-decomposition, Q and R are both \(J'_h\)-symplectic.
Proof
Direct from the explicit Iwasawa decomposition given by [40].
In the following, \(X^{-s}\) represents the matrix whose coefficients are the coefficients of \(X^{-1}\) exchanged over the antidiagonal.
Lemma 3
(Elementary \({\varvec{J}}_{{\varvec{h}}}'\) -symplectic matrices).
-
For any \(A\in \text {GL}(q_h,\mathbf {K}_h)\), \(\begin{pmatrix} A &{} 0 \\ 0 &{} A^{-s} \end{pmatrix}\) is \(J_{h}'\)-symplectic.
-
For any \(A\in \text {GL}(2,\mathbf {K}_h)\) with \(\det A=1\) the block matrix \(\small {\begin{pmatrix} \text {Id}_{q_h-1} &{} 0 &{} 0 \\ 0 &{} A &{} 0 \\ 0 &{} 0 &{} \text {Id}_{q_h-1} \end{pmatrix}}\) is \(J_{h}'\) symplectic.
We now turn to the shape of triangular \(J_{h}'\) symplectic matrices.
Lemma 4
Block triangular symplectic matrices are exactly the matrices of the form \( \begin{pmatrix} A &{} AU \\ 0 &{} A^{-s} \end{pmatrix} \) where \(U=U^s\).
As we know the elementary operations that preserve the symplectism, we can use these transformations to effectively reduce a symplectic lattice.
 Consider M a \(J_{h}'\)-symplectic matrix, we want to size-reduce using the symmetries existing by symplecticity. Let first take the R part of the QR-decomposition of M and make appear the factors A and U as in Lemma 4. Then, we can focus on the left-upper matrix A and size-reducing it into a matrix \(A'\). All elementary operations performed are also symmetrically applied on \(A^s\) to obtain \((A')^s\). Eventually the size reduction is completed by dealing with the upper-right block, which is done by computing a global multiplication by
Consider M a \(J_{h}'\)-symplectic matrix, we want to size-reduce using the symmetries existing by symplecticity. Let first take the R part of the QR-decomposition of M and make appear the factors A and U as in Lemma 4. Then, we can focus on the left-upper matrix A and size-reducing it into a matrix \(A'\). All elementary operations performed are also symmetrically applied on \(A^s\) to obtain \((A')^s\). Eventually the size reduction is completed by dealing with the upper-right block, which is done by computing a global multiplication by

The corresponding algorithm is given in Algorithm 5. The recursive lattice reduction algorithm using the symplecticity is the same algorithm as Algorithm 4, where the size-reduction call of line 4 is replaced by
 . The size reduction property on \(A'\) implies that both \(A'\) and \(A'^{-1}\) are small, and therefore it is easy to check that the same is true for the now reduced \(R'\) and of course for the corresponding size reduction of the matrix M itself.
. The size reduction property on \(A'\) implies that both \(A'\) and \(A'^{-1}\) are small, and therefore it is easy to check that the same is true for the now reduced \(R'\) and of course for the corresponding size reduction of the matrix M itself.

This approach admits several algorithmic optimizations:
-
Only the first half of the matrix R is actually needed to perform the computation since we can retrieve the other parts. Indeed, with the equation \(QR=M\), R is upper triangular and it only depends on the first half of Q.
-
We compute only the part above the antidiagonal of AU. This is actually enough to compute the part above the antidiagonal of \(A^{-1}(AU)\), which is persymmetric.
-
An interesting implication is that since we need to compute only half of the QR decomposition, we need (roughly) only half the precision.
Remark 4
To perform the fast size-reduction, we used the descended form \(J_h'\). However, the
 algorithm will then call reduction of some rank 2 modules over \(\mathbf {K}_{h-1}\). For the reduction of these modules, we will then use the form \(J_{h-1}\), and its descent \(J'_{h-1}\) over the field \(\mathbf {K}_{h-2}\) and so on.
algorithm will then call reduction of some rank 2 modules over \(\mathbf {K}_{h-1}\). For the reduction of these modules, we will then use the form \(J_{h-1}\), and its descent \(J'_{h-1}\) over the field \(\mathbf {K}_{h-2}\) and so on.
4.4 Improved Complexity
We analyze the algorithm of Sect. 3 with the size-reduction of Sect. 4.3. By Lemma 3, we can use the transition matrix found after a reduction in the first half of the matrix to directly reduce the second half of the matrix. This means that in the symplectic reduction, we have recursive calls only for the first \(q_h\) steps of the tour at the toplevel of reduction. These are the only modifications to append to our algorithm. Remark that, during the entire algorithm, the R-part of the QR decomposition of the currently reduced basis remains symplectic.
To estimate the analysis we use an experimentally validated heuristic on the repartition of the potential during the reduction, which can be stated as follows:
Heuristic 2
The half-potential \(\varPi =\sum _{i=1}^{q_h} \left( q_h+1-i\right) \log \mathcal {N}_{\mathbf {L}/\mathbf {Q}}(R_{i,i})\) is, at the end of
 , always larger than the potential of an orthogonal matrix with the same volume.
, always larger than the potential of an orthogonal matrix with the same volume.
Remark 5
Heuristic 2 hinges on the fact that the sequence of \(\mathcal {N}_{\mathbf {L}/\mathbf {Q}}(R_{i,i})\) is non-increasing, which is the case in practice for random lattices.
Claim 2
Let f a power of \(q=\text {O}\left( \log f\right) \) integer and \(n=\varphi (f)\). Under Heuristic 1 and 2, the complexity for reducing a 2-dimensional matrix M over \(\mathbf {L}=\mathbf {Q}[x]/\varPhi _f(x)\) with condition number C is

Moreover, the first column of the reduced matrix has coefficients bounded by

For \(C=n^{\omega (1)}\) and \(\varepsilon =\omega (1)\), we get a running time of \(n^{2+\frac{\log (1/2+1/2q)}{\log q}+o\left( 1\right) }C\).
Remark 6
This conjecture uses the condition number C instead of the classical bit length B of the matrix. In practice in cryptography, matrices are well-conditioned and we can take \(C=B\). This is in particular the case of Coppersmith matrices. In the worst case, C can be as large as nB. Since the number of operations is smaller than \(O(n^2B)\), a single step of linear algebra is more costly than these operations. The condition number is a finer measure of the complexity in linear algebra [15, 18] and we use Seysen algorithm [43] to compute the size-reduction more efficiently in [23].
5 Optimizations and Implementation
5.1 About the Implementation Used
The proof-of-concept program was written in the interpreted language Pari/gp [4]. It uses the native functions for multiplying field elements, which is not at all optimal, and even more so when we multiply matrices. Only the recursive calls were parallelized, and not the Gram-Schmidt orthogonalization nor the size reduction, which limits the speed-up we can achieve in this way. We used the Householder method for the QR decomposition. The symplectic optimization was used at each step and was not found to change the quality of the reduction. We now turn to two examples to showcase the efficiency of this program.
The algorithms given in Sect. 3 and Sect. 4 have been implemented and tested. Here, we give various optimizations and implementation choices, as well as an experimental assessment on the heuristics used in the complexity proofs.
5.2 On the Choice of the Base Case
Let \(h>0\) be a non-negative integer. The setting of the reduction is a tower of power-of-two cyclotomic fields \(\mathbf {K}_h^\uparrow = \left( \mathbf {Q}= \mathbf {K}_0 \subset \mathbf {K}_1 \subset \cdots \subset \mathbf {K}_h=\mathbf {L}\right) \).
Stopping the reduction before hitting Z. As stated before, the approximation factor increases quickly with the height of the tower. However, if we know how to perform a reduction over a number field above \(\mathbf {Q}\), say \(\mathbf {K}_1\) for instance, directly, then there is no need to reduce up to getting a \(\mathbf {Z}\)-module and we instead stop at this level. Actually, the largest the ring, the better the approximation factor becomes and the more efficient is the whole routine. It is well-known that it is possible to come up with a direct reduction algorithm for an algebraic lattice when the underlying ring of integer is norm-Euclidean, as first mentioned by Napias in [33]. The reduction algorithm over such a ring \(\mathcal {O}_\mathbf {K}\) can be done exactly as for the classical lll algorithm, by replacing the norm over \(\mathbf {Q}\) by the algebraic norm over \(\mathbf {K}\). Hence a natural choice would be \(\mathbf {Z}[x]/(x^n+1)\) with \(n\leqslant 8\) as these rings are proved to be norm-Euclidean.
 However, it turns out that while \(\mathbf {K}= \mathbf {Z}[x]/(x^{16}+1)\) is not norm-Euclidean, we can still use this as our base case. As such, we need to slightly change the algorithm in case of failure of the standard algorithm. We denote by \(\{x\}\), the fractional part of x. Given \(a,b\in \mathbf {K}\) given by an embedding representation with complex numbers, we can compute \(\sqrt{\{\mu \}}\) (computed coefficient-wise), with \(\mu =a/b\). We can compute the randomized unit rounding of \(\sqrt{\{\mu \}}\) using Theorem 1, which outputs a unit u such that \(u^2\{\mu \}\) is rounded. We change the Lovász condition to
However, it turns out that while \(\mathbf {K}= \mathbf {Z}[x]/(x^{16}+1)\) is not norm-Euclidean, we can still use this as our base case. As such, we need to slightly change the algorithm in case of failure of the standard algorithm. We denote by \(\{x\}\), the fractional part of x. Given \(a,b\in \mathbf {K}\) given by an embedding representation with complex numbers, we can compute \(\sqrt{\{\mu \}}\) (computed coefficient-wise), with \(\mu =a/b\). We can compute the randomized unit rounding of \(\sqrt{\{\mu \}}\) using Theorem 1, which outputs a unit u such that \(u^2\{\mu \}\) is rounded. We change the Lovász condition to
which is now randomized and we restart up to a hundred times if it fails. This algorithm restarts on average 0.7 times and fails every 50000 times. On failure, one can, for example, use a more complicated approach; but as long as the number of bits is not gigantic, we can simply stop there since the other reductions around the two Gram-Schmidt norms will randomize everything and the algorithm can smoothly continue. The terms a, b tend to slowly accumulate a unit contribution when \(n\geqslant 4\), and it is therefore needed to rebalance them using randomized rounding. For \(n=16\), this happens on average every 50 times.
Comparison between the base fields. We give in the Table 1 the properties of the various possible base cases between dimension 1 over \(\mathbf {Q}\)—that is \(\mathbf {Q}\) itself—and 16, as described above.
Remark 7
We need the base case to be (relatively) fast in our implementation. To speed-up the reduction, even more, we followed the standard divide-and-conquer strategy: we first reduce the input matrix with half the precision, apply the transition matrix, and reduce the rest with about half the precision.
5.3 Decreasing the Approximation Factor
In several applications, it is interesting to decrease the approximation factor. To do so our technique is, at the lowest level of recursion, and when the precision is sufficiently low, to use a lll-type algorithm. Each time the reduction is finished, we descend the matrix to a lower level where the approximation factor is lower. Since the basis is already reduced (over the upper field), it is in particular well-conditioned and the running-time of the this “over-reductions pass” is a fraction of the first reduction. In particular, in practice, we can recover the same approximation factor as the regular lll algorithm (over \(\mathbf {Z}\)) for approximately the same cost as doing the reduction over the upper tower. Hence, for practical applications, we can consider that the defect of approximation factor induced by our algorithm to be inexistent compare to lll.
Remark 8
This can be compared with some experimental strategies of the fplll [44] library where a first pass of reduction is performed at low precision and an over-pass is done right after to ensure the desired approximation factor.
5.4 Lifting a Reduction
One might expect that, as soon as the ideal generated by all the \(\mathcal {N}_{\mathbf {L}/\mathbf {K}}(a_i)\) and \(\mathcal {N}_{\mathbf {L}/\mathbf {K}}(b_i)\) is \(\mathcal {O}_\mathbf {K}\), that for most of the small \(x\in \mathcal {O}_\mathbf {L}\), we would have
There is, however, a profusion of counterexamples to this and the algorithm often stumbles on them. This implies that the lift of a short vector can actually be quite large, depending on the norm of the ideal generated by the elements \(\mathcal {N}_{\mathbf {L}/\mathbf {K}}({\langle {a}\,|\,{x} \rangle )}\) and \(\mathcal {N}_{\mathbf {L}/\mathbf {K}}({\langle {b}\,|\,{x} \rangle )}\). A solution that practically works is to increase the number of short vectors we consider in the lifting phase: instead of lifting one vector, we lift multiple of them. As such, the lift step never causes problem when we are reducing a random lattice. In our experiments with random lattices, the average number of lifted vectors is around 1.5. To understand why the number of repetition is so low, we can model the coefficients of the lifted vector in the original basis as being random elements of \(\mathcal {O}_\mathbf {L}\)Footnote 5. As such, since we need our lifted vector to be primitive, we want its coefficients to be coprime. It is knownFootnote 6 that the density of pairs of coprime algebraic integers is \(1/\zeta _\mathbf {L}(2)\) where \(\zeta _\mathbf {L}\) is the zeta function of the field \(\mathbf {L}\). For fields in which the reduction is tractable, this value is indeed sufficiently big so that the number of required repetitions is very small.
When the lattice is not random, for example with a short planted element, it sometimes completely fails: at each round in the algorithm, the lift will return a long vector even if the recursive reduction found plenty of short ones. While this may not be a problem for some applications – finding a short vector in a NTRU lattice implies an ability to decrypt – it is an important one for others. Our proposed solution to this difficulty is to use a pseudo-basis instead of a basis. Indeed, it is a standard fact that the first element can be lifted into a unimodular pseudo-basis [7, Corollary 1.3.5]. From that result, we can control precisely the norm of the lifted pseudo-element. However, as pseudo-bases consist of vectors and ideals, the elementary operations on this representation require ideal arithmetic in \(\mathcal {O}_\mathbf {K}\). As such, we need to have a fast ideal arithmetic in these rings or the bottleneck of the reduction would become these operations. Getting faster arithmetic from the reduction process itself is however not straightforward.
6 Applications
6.1 Attacks on Multilinear Maps
In 2013, a construction for cryptographic multilinear maps was announced [13] by Garg, Gentry and Halevi with a heuristic security claim. An implementation of an optimization of the scheme was later published [3] by Albrecht et al.; however some of its uses, in particular involving an encoding of zero, were broken [19] by Hu and Jia. Subsequently, subfield attacks showed that the previous choice of parameters was unsafe [2, 6, 24], but these attacks were only asymptotical due to the extremely large dimension and length of the integers involved.
The improved scheme [3] gives encoding of the form \(u_i=e_i/z \bmod q\) where \(\Vert e_i\Vert \) is around \(28\mathrm {e}N^4 \log (N)^{3/2} \sqrt{\pi \log (8N)}\) in the ring \(\mathbf {Z}[x]/(x^N+1)\) with N a power of two. The attack, attributed to Galbraith, consists in computing \(u_1/u_2=e_1/e_2\) and recovering short vectors in
which is manifestly solving a ntru-like problem.
The present work revisits the results of the attacks presented in [24]: many instances can be broken even with a high approximation factor. A simple instance is with \(N=2^{16}\) and \(q\approx 2^{6675}\), rated at the time at 56 bits of security [3, Table 1]. We compute the norm of \(e_1/e_2\) over \(\mathbf {Z}[x]/(x^n+1)\) with \(n=2^{11}\) and solve the lattice problem over this smaller field. It took 13 core-days and 4 wall-time days to compute a solution. There are few running times of lattice reduction with high approximation factor on hard instances in the literature. It was reported in 2016 [2, Table 6] that the same problem with \(n=2^8\) and \(q\approx 2^{240}\) takes 120 (single-threaded) hours with fplll [44]. As the complexity of their implementation is roughly proportional to \(n^4\log (q)^2\) we can estimate a running time of 40000 years, or 4000000 times slower than the algorithm presented in this work. This is the largest hard instanceFootnote 7 of lattice reduction that we found in the literature.
6.2 Gentry-Szydlo Algorithm
The fast reduction procedure for cyclotomic ideals can be used to build a fast implementation of the Gentry-Szydlo algorithm [14]. This algorithm retrieves, in polynomial time, a generator of a principal ideal \(f\mathcal {O}_\mathbf {K}\) given its relative norm \(f\overline{f}\) in cyclotomic fields, or more generally in CM fields. This algorithm is a combination of algebraic manipulations of ideals in the field and lattice reduction.
On the Gentry-Szydlo algorithm. The Gentry-Szydlo algorithm [14] aims at solving the following problem, presented in its whole generality:
Problem 1
(Principal ideal problem with known relative norm). Let \(\mathbf {L}\) be a CM-field, of conjugation \(x\mapsto \overline{x}\), and denote by \(\mathbf {L}^+\) its maximal totally real subfield. Let \(f\in \mathcal {O}_\mathbf {L}\) and set \(\mathfrak {f} = f\mathcal {O}_\mathbf {L}\), the ideal spanned by this algebraic integer. Given the relative norm \(\mathcal {N}_{\mathbf {L}/\mathbf {L}^+}(f) = f\overline{f}\) and a \(\mathbf {Z}\)-basis of the ideal \(\mathfrak {f}\), retrieve the element f.
It was proved by Lenstra and Silverberg that this problem can be solved in deterministic polynomial time [28]. Among the numerous applications of this algorithm, we shall highlight its use in cryptanalysis when some lattice-based scheme is leaking [2, 10, 14], for finding a generator of an ideal [5], and for solving geometric problems on ideals [13, 22].
The idea of this process can be exposed as follows: from \(\mathfrak {f}\) and \(f\overline{f}\) we start by reducing the \(\mathcal {O}_\mathbf {L}\)-lattice \(\frac{f\mathcal {O}_\mathbf {L}}{\sqrt{f\overline{f}}}\), of volume \(\sqrt{|\varDelta _\mathbf {L}|}\) and find an element of the shape fx where \(x\in \mathcal {O}_\mathbf {L}\) and is small (say \(\Vert x\Vert =2^{\widetilde{\text {O}}\left( n\right) }\)). Now we have that:
As \(x\overline{x}=\frac{fx\overline{fx}}{f\overline{f}}\), we have reduced the problem to the smaller instance \(\left( \overline{x}\mathcal {O}_\mathbf {L}, x\overline{x}\right) \).
For the sake of simplicity, we give here the outline of the remaining part of the algorithm for a cyclotomic field of conductor a power of two. The algorithm selects an integer e such that \(f^e \mod r\) is known with a large r. Binary exponentiation with the above reduction computes a \(x\mathcal {O}_\mathbf {L}\) with a short \(x\in \mathcal {O}_\mathbf {L}\) and such that \(f^e=Px\) with P known (and invertible) modulo r and \(q^k\). Now we can deduce \(x \bmod r\) and since x is small, we know x.
The last step is to extract an e-th root modulo \(q^k\). We choose q such that \(q\mathcal {O}_\mathbf {L}=\mathfrak {q}\mathfrak {\overline{q}}\) which always exists in power of two cyclotomic fields since the group \((\mathbf {Z}/2n\mathbf {Z})^\times /\{-1,1\}\) is cyclic. Extracting e-th root modulo \(\mathfrak {q}\) is easy, as e is smooth. There are \(\gcd (e,q^{n/2}-1)\) such roots, and we can choose q such that for each p|e with p not a Fermat prime, \(q^{n/2}\ne 1 \bmod p\). If we choose \(f \bmod \mathfrak {q}\) as a root, then we know \(\overline{f} \bmod \overline{\mathfrak {q}}\), and we also know \(f\overline{f}\) so we can deduce \(f \bmod \overline{\mathfrak {q}}\). As a result, we know \(f \bmod q\) and Hensel lifting leads to \(f \bmod q^k\). For k sufficiently large, we recover f.
We choose e to be the smallest multiple of 2n, so that r, the product of primes p such that \(2n|p-1|e\), is sufficiently large. One can show [22] that \(\log e=O(\log n \log \log n)\) is enough and heuristically taking e as the product of n and a primorial reaches this bound.
Faster multiplication using lattice reduction. The bottleneck of the Gentry-Szydlo algorithm is to accelerate the ideal arithmetic. We represent ideals with a small family of elements over the order of a subfield \(\mathcal {O}_{\mathbf {K}}\). One can represent the product of two ideals using the family of all products of generators. However, this leads to a blow-up in the size of the family. A reasonable approach is simply to sample a bit more than \([\mathbf {L}:\mathbf {K}]\) random elements in the product so that with overwhelming probability the ideal generated by these elements is the product ideal itself. It then suffices to reduce the corresponding module to go back to a representation with smaller generators.
An important piece is then the reduction of an ideal itself. Our practical approach is here to reduce a square matrix of dimension \([\mathbf {L}:\mathbf {K}]\), and every two rounds to add a new random element with a small Gram-Schmidt norm in the ideal at the last position. With these techniques, the overall complexity of the Gentry-Szydlo now becomes a \(\tilde{O}(n^3)\).
In our experiment, we reduce up to \(1.05^n\) (respectively \(1.1^n\)) the first ideal to accelerate the powering with \(n\leqslant 512\) (respectively \(n=1024\)). The smallest e such that this approximation works at the end was chosen. The other reductions are done with an approximation factor of \(2^{n/5}\) (respectively \(2^{n/3}\)) (Table 2).
We emphasize that the implementation hardly used all cores: for example, the total running time over all cores in the last case was 354 h.
7 Conclusion
In this article, we presented two very efficient reduction algorithms for reducing lattices defined over the ring of integers of cyclotomic fields, which exploit the recursive structure of tower of their subfields. The first algorithm has a complexity close to the number of swaps \(\text {O}\left( n^2B\right) \) in lll and the second one exploits the symplectic symmetries naturally present in such towers and goes even below this bound. One caveat of them is that their approximation factors are worse than the classical lll approximation factor. However, such algorithms are nonetheless useful for various applications, such as breaking graded encoding schemes or manipulating ideals, as in the Gentry-Szydlo algorithm. We implemented all our algorithms and their observed performances are close to the complexities that we estimate under some assumptions. In particular, our implementation reduces to large base cases, that is all power of two cyclotomic fields of dimension \(\leqslant 16\).
Our claims rely on some heuristics we introduce to justify their validity. It would be nice to provide a rigorous complexity analysis in a relevant computational model. It is possible to completely remove Heuristic 1 by using the pseudo-basis representation of modules over Dedekind rings. We also leave as future work the question of programming the algorithms in a more efficient language and to empirically compare our claimed complexities with the experimental ones.
Notes
- 1.
The approximation factor loss appearing with this technique is not increasing the approximation factor of the whole dbkz routine, as it acts only as a polynomial control of the bitsize of the elements and to transform generating families of lattices to bases without degrading the size of the vectors.
- 2.
In whole generality, it is not necessarily free, but imposing both fields to be cyclotomics is sufficient to imply this property.
- 3.
We defer the precise computation of this constant to [23].
- 4.
The precise definition of this completion and lifting is given in a dedicated paragraph.
- 5.
For a distribution which cannot be quantified in closed form, however.
- 6.
As a generalization of the fact that the density of coprime integers is \(1/\zeta (2)\).
- 7.
References
Ajtai, M.: Generating hard instances of lattice problems (extended abstract). In: 28th STOC, pp. 99–108. ACM, May 1996
Albrecht, M., Bai, S., Ducas, L.: A subfield lattice attack on overstretched NTRU assumptions - cryptanalysis of some FHE and graded encoding schemes. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part I. LNCS, vol. 9814, pp. 153–178. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_6
Albrecht, M.R., Cocis, C., Laguillaumie, F., Langlois, A.: Implementing candidate graded encoding schemes from ideal lattices. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015, Part II. LNCS, vol. 9453, pp. 752–775. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_31
Batut, C., Belabas, K., Bernardi, D., Cohen, H., Olivier, M.: PARI-GP (1998). ftp://megrez.math.u-bordeaux.fr/pub/pari
Biasse, J.-F., Espitau, T., Fouque, P.-A., Gélin, A., Kirchner, P.: Computing generator in cyclotomic integer rings - a subfield algorithm for the principal ideal problem in L\(_{|{{\varDelta }{\mathbb{K}|}}}(\frac{1}{2})\) and application to the cryptanalysis of a FHE scheme. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 60–88. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_3
Cheon, J.H., Jeong, J., Lee, C.: An algorithm for NTRU-problems, cryptanalysis of the GGH multilinear map without an encoding of zero. In: ANTS (2016)
Cohen, H.: Advanced topics in Computational Number Theory, vol. 193. Springer, Heidelberg (2012)
Coppersmith, D.: Small solutions to polynomial equations, and low exponent RSA vulnerabilities. J. Cryptol. 10(4), 233–260 (1997). https://doi.org/10.1007/s001459900030
Cramer, R., Ducas, L., Peikert, C., Regev, O.: Recovering short generators of principal ideals in cyclotomic rings. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 559–585. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_20
Espitau, T., Fouque, P.-A., Gérard, B., Tibouchi, M.: Side-channel attacks on BLISS lattice-based signatures: exploiting branch tracing against strongSwan and electromagnetic emanations in microcontrollers. In: Thuraisingham, B.M., Evans, D., Malkin, T., Xu, D. (eds.) CCS 2017, pp. 1857–1874. ACM (2017)
Gama, N., Howgrave-Graham, N., Nguyen, P.Q.: Symplectic lattice reduction and NTRU. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 233–253. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_15
Gama, N., Nguyen, P.Q.: Finding short lattice vectors within Mordell’s inequality. In: Ladner, R.E., Dwork, C. (eds.) 40th STOC, pp. 207–216. ACM (2008)
Garg, S., Gentry, C., Halevi, S.: Candidate multilinear maps from ideal lattices. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 1–17. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_1
Gentry, C., Szydlo, M.: Cryptanalysis of the revised NTRU signature scheme. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 299–320. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_20
Golub, G.H., Van Loan, C.F.: Matrix Computations, 3rd edn. The Johns Hopkins University Press, Baltimore (1996)
Hanrot, G., Pujol, X., Stehlé, D.: Analyzing blockwise lattice algorithms using dynamical systems. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 447–464. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_25
Heckler, C., Thiele, L.: Complexity analysis of a parallel lattice basis reduction algorithm. SIAM J. Comput. 27(5), 1295–1302 (1998)
Higham, N.J.: Accuracy and Stability of Numerical Algorithms. SIAM, Philadelphia (2002)
Hu, Y., Jia, H.: Cryptanalysis of GGH map. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part I. LNCS, vol. 9665, pp. 537–565. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_21
Kannan, R.: Improved algorithms for integer programming and related lattice problems. In: Johnson, D.S., et al. (eds.) Symposium on Theory of Computing, pp. 193–206. ACM (1983)
Kim, T., Lee, C.: Lattice reductions over Euclidean rings with applications to cryptanalysis. In: O’Neill, M. (ed.) IMACC 2017. LNCS, vol. 10655, pp. 371–391. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-71045-7_19
Kirchner, P.: Algorithms on ideal over complex multiplication order. Cryptology ePrint Archive, Report 2016/220 (2016)
Kirchner, P., Espitau, T., Fouque, P.-A.: Algebraic and euclidean lattices: optimal lattice reduction and beyond. Cryptology ePrint Archive, Report 2019/1436 (2019)
Kirchner, P., Fouque, P.-A.: Revisiting lattice attacks on overstretched NTRU parameters. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 3–26. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_1
Langlois, A., Stehlé, D.: Worst-case to average-case reductions for module lattices. Des. Codes Crypt. 75(3), 565–599 (2014). https://doi.org/10.1007/s10623-014-9938-4
Lee, C., Pellet-Mary, A., Stehlé, D., Wallet, A.: An LLL algorithm for module lattices. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019, Part II. LNCS, vol. 11922, pp. 59–90. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34621-8_3
Lenstra, A.K., Lenstra, H.W.J., Lovász, L.: Factoring polynomials with rational coefficients. Math. Ann. 261, 515–534 (1982)
Lenstra, H.W.J., Silverberg, A.: Testing isomorphism of lattices over CM-orders. SIAM J. Comput. 48(4), 1300–1334 (2019)
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_1
Mehlhorn, K., Sanders, P.: Algorithms and Data Structures: The Basic Toolbox. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-77978-0
Micciancio, D., Walter, M.: Practical, predictable lattice basis reduction. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part I. LNCS, vol. 9665, pp. 820–849. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_31
Mukherjee, T., Stephens-Davidowitz, N.: Lattice reduction for modules, or how to reduce Module-SVP to Module-SVP. Cryptology ePrint Archive, Report 2019/1142 (2019). Accepted to Crypto 2020
Napias, H.: A generalization of the LLL-algorithm over Euclidean rings or orders. J. théorie nombres Bordeaux 8(2), 387–396 (1996)
Neukirch, J.: Algebraic Number Theory. Springer, Heidelberg (1988)
Neumaier, A., Stehlé, D.: Faster LLL-type reduction of lattice bases, In: International Symposium on Symbolic and Algebraic Computation, ISSAC, pp. 373–380. ACM (2016)
Nguên, P.Q., Stehlé, D.: Floating-point LLL revisited. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 215–233. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_13
Novocin, A., Stehlé, D., Villard, G.: An LLL-reduction algorithm with quasi-linear time complexity: extended abstract. In: Fortnow, L., Vadhan, S.P. (eds.) 43rd STOC, pp. 403–412. ACM Press, June 2011
Pornin, T., Prest, T.: More efficient algorithms for the NTRU key generation using the field norm. In: Lin, D., Sako, K. (eds.) PKC 2019, Part II. LNCS, vol. 11443, pp. 504–533. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17259-6_17
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N., Fagin, R. (eds.) 37th STOC, pp. 84–93. ACM Press (2005)
Sawyer, P.: Computing Iwasawa decomposition of classical Lie groups of noncompact type using QR-decomposition. Linear Algebra Appl. 493, 573–579 (2016)
Schnorr, C., Euchner, M.: Lattice basis reduction: improved practical algorithms and solving subset sum problems. Math. Program. 66, 181–199 (1994). https://doi.org/10.1007/BF01581144
Schönhage, A.: Fast reduction and composition of binary quadratic forms. In: International Symposium on Symbolic and Algebraic Computation, ISSAC 1991, pp. 128–133. ACM (1991)
Seysen, M.: Simultaneous reduction of a lattice basis its reciprocal basis. Combinatorica 13(3), 363–376 (1993)
The FPLLL development team FPLLL, a lattice reduction library (2016). https://github.com/fplll/fplll
Villard, G.: Parallel lattice basis reduction. In: International Symposium on Symbolic and Algebraic Computation, ISSAC 1992, pp. 269–277. ACM (1992)
Acknowledgment
We would like to thank Bill Allombert for his help in the parallelization of the program and Léo Ducas and Damien Stehlé for interesting discussions. Part of this work was done while the authors were visiting the Simons Institute for the Theory of Computing in February 2020. This work is supported by the European Union H2020 program under grant agreements ERC-669891 and Prometheus Project-780701.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Kirchner, P., Espitau, T., Fouque, PA. (2020). Fast Reduction of Algebraic Lattices over Cyclotomic Fields. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12171. Springer, Cham. https://doi.org/10.1007/978-3-030-56880-1_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-56880-1_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56879-5
Online ISBN: 978-3-030-56880-1
eBook Packages: Computer ScienceComputer Science (R0)




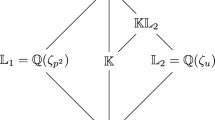



 preserves the determinant by construction and reduces the norm of the coefficients, we can use it to reduce the bitsize of u, v to (roughly) the bitsize of a and b.
preserves the determinant by construction and reduces the norm of the coefficients, we can use it to reduce the bitsize of u, v to (roughly) the bitsize of a and b.