Skip to main content
Springer Nature Link
Log in

A Batch Scheduling Problem of Automatic Drug Dispensing System in Outpatient Pharmacy

  • Conference paper
  • First Online:
Algorithmic Aspects in Information and Management (AAIM 2020)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 12290))

Included in the following conference series:

  • 943 Accesses

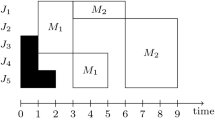
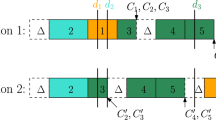
Abstract

This paper studies the batch scheduling problem with incompatible job families which can be applied to the automatic drug dispensing of outpatient pharmacies. We prove that the problem is strongly NP-hard even if the processing time and the weight of each job are same, and we propose a pseudo-polynomial time algorithm for the special case where the jobs of each family have a common due date.

Supported by the National Natural Science Foundation of China (No. 11601316) and discipline “Applied Mathematics” of Shanghai Polytechnic University (No. XXKPY1604).

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Liu, L., Tang, G., Fan, B., Wang, X.: Two-person cooperative games on scheduling problems in outpatient pharmacy dispensing process. J. Comb. Optim. 30(4), 938–948 (2015). https://doi.org/10.1007/s10878-015-9854-1

    Article  MathSciNet  MATH  Google Scholar 

  2. Fan, J., Lu, X.: Supply chain scheduling problem in the hospital with periodic working time on a single machine. J. Comb. Optim. 30(4), 892–905 (2015). https://doi.org/10.1007/s10878-015-9857-y

    Article  MathSciNet  MATH  Google Scholar 

  3. Wang, D., Liu, F., Yin, Y., Wang, J., Wang, Y.: Prioritized surgery scheduling in face of surgeon tiredness and fixed off-duty period. J. Comb. Optim. 30(4), 967–981 (2015). https://doi.org/10.1007/s10878-015-9846-1

    Article  MathSciNet  MATH  Google Scholar 

  4. Yang, Y., Shen, B., Gao, W., Liu, Y., Zhong, L.: A surgical scheduling method considering surgeons preferences. J. Comb. Optim. 30, 1016–1026 (2015)

    Article  MathSciNet  Google Scholar 

  5. Zhang, X., Wang, H., Wang, X.: Patients scheduling problems with deferred deteriorated functions. J. Comb. Optim. 30(4), 1027–1041 (2015). https://doi.org/10.1007/s10878-015-9852-3

    Article  MathSciNet  MATH  Google Scholar 

  6. Zhang, L., Zhang, Y., Bai, Q.: Two-stage medical supply chain scheduling with an assignable common due window and shelf life. J. Comb. Optim. 37(1), 319–329 (2017). https://doi.org/10.1007/s10878-017-0228-8

    Article  MathSciNet  MATH  Google Scholar 

  7. Li, W., Chai, X.: The medical laboratory scheduling for weighted flow-time. J. Comb. Optim. 37(1), 83–94 (2017). https://doi.org/10.1007/s10878-017-0211-4

    Article  MathSciNet  MATH  Google Scholar 

  8. Uzsoy, R.: Scheduling batch processing machines with incompatible job families. Int. J. Prod. Res. 33, 2685–2708 (1995)

    Article  Google Scholar 

  9. Mehta, S., Uzsoy, R.: Minimizing total tardiness on a batch processing machine with incompatible job families. IIE Trans. 30, 165–178 (1998)

    Google Scholar 

  10. Jolai, F.: Minimizing number of tardy jobs on a batch processing machine with incompatible job families. Eur. J. Oper. Res. 162, 184–190 (2005)

    Article  MathSciNet  Google Scholar 

  11. Perez, I., Fowler, J., Carlyle, W.: Minimizing total weighted tardiness on a single batch process machine with incompatible job families. Comput. Oper. Res. 32, 327–341 (2005)

    Article  MathSciNet  Google Scholar 

  12. Liu, L., Ng, C., Cheng, T.: On the complexity of bi-criteria scheduling on a single batch processing machine. J. Sched. 13, 629–638 (2010)

    Article  MathSciNet  Google Scholar 

  13. Karp, R.: Reducibility among combinatorial problems. In: Miller, R.E., Thatcher, J.W. (eds.) Complexity of Computer Computaitons, pp. 85–103. Plenum Press, New York (1972)

    Chapter  Google Scholar 

  14. Brucker, P.: Theory of Scheduling. Springer, Berlin (1995)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Arts and Sciences, Shanghai Polytechnic University, Shanghai, 201209, China

    Lili Liu

  2. Shanghai General Hospital, School of Medicine, Shanghai Jiaotong University, Shanghai, 200080, China

    Chunyu Fu

Authors
  1. Lili Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chunyu Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chunyu Fu .

Editor information

Editors and Affiliations

  1. Zhejiang Normal University, Jinhua, China

    Zhao Zhang

  2. Texas Southern University, Houston, TX, USA

    Wei Li

  3. University of Texas at Dallas, Richardson, TX, USA

    Ding-Zhu Du

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Liu, L., Fu, C. (2020). A Batch Scheduling Problem of Automatic Drug Dispensing System in Outpatient Pharmacy. In: Zhang, Z., Li, W., Du, DZ. (eds) Algorithmic Aspects in Information and Management. AAIM 2020. Lecture Notes in Computer Science(), vol 12290. Springer, Cham. https://doi.org/10.1007/978-3-030-57602-8_48

Download citation

  • DOI: https://doi.org/10.1007/978-3-030-57602-8_48

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-030-57601-1

  • Online ISBN: 978-3-030-57602-8

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics