Abstract
We present a novel 3D pose refinement approach based on differentiable rendering for objects of arbitrary categories in the wild. In contrast to previous methods, we make two main contributions: First, instead of comparing real-world images and synthetic renderings in the RGB or mask space, we compare them in a feature space optimized for 3D pose refinement. Second, we introduce a novel differentiable renderer that learns to approximate the rasterization backward pass from data instead of relying on a hand-crafted algorithm. For this purpose, we predict deep cross-domain correspondences between RGB images and 3D model renderings in the form of what we call geometric correspondence fields. These correspondence fields serve as pixel-level gradients which are analytically propagated backward through the rendering pipeline to perform a gradient-based optimization directly on the 3D pose. In this way, we precisely align 3D models to objects in RGB images which results in significantly improved 3D pose estimates. We evaluate our approach on the challenging Pix3D dataset and achieve up to 55% relative improvement compared to state-of-the-art refinement methods in multiple metrics.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Recently, there have been significant advances in single image 3D object pose estimation thanks to deep learning [7, 32, 42]. However, the accuracy achieved by today’s feed-forward networks is not sufficient for many applications like augmented reality or robotics [8, 44]. As shown in Fig. 1, feed-forward networks can robustly estimate the coarse high-level 3D rotation and 3D translation of objects in the wild (left) but fail to predict fine-grained 3D poses (right) [48].
To improve the accuracy of predicted 3D poses, refinement methods aim at aligning 3D models to objects in RGB images. In this context, many methods train a feed-forward network that directly predicts 3D pose updates given the input image and a 3D model rendering under the current 3D pose estimate [23, 38, 52]. In contrast, more recent methods use differentiable rendering [27] to explicitly optimize an objective function conditioned on the input image and renderer inputs like the 3D pose [17, 34]. These methods yield more accurate 3D pose updates because they exploit prior knowledge about the rendering pipeline.
Given an initial 3D pose predicted by a feed-forward network (left), we predict deep cross-domain correspondences between real-world RGB images and synthetic 3D model renderings in the form of geometric correspondence fields (middle) that enable us to refine the 3D pose in a differentiable rendering framework (right). (Color figure online)
However, existing approaches based on differentiable rendering have significant shortcomings because they rely on comparisons in the RGB or mask space. First, methods which compare real-world images and synthetic renderings in the RGB space require photo-realistic 3D model renderings [27]. Generating such renderings is difficult because objects in the real world are subject to complex scene lighting, unknown reflection properties, and cluttered backgrounds. Moreover, many 3D models only provide geometry but no textures or materials which makes photo-realistic rendering impossible [39]. Second, methods which rely on comparisons in the mask space need to predict accurate masks from real-world RGB images [17, 34]. Generating such masks is difficult even using state-of-the-art approaches like Mask R-CNN [11]. Additionally, masks discard valuable object shape information which makes 2D-3D alignment ambiguous. As a consequence, the methods described above are not robust in practice. Finally, computing gradients for the non-differentiable rasterization operation in rendering is still an open research problem and existing approaches rely on hand-crafted approximations for this task [14, 17, 27].
To overcome these limitations, we compare RGB images and 3D model renderings in a feature space optimized for 3D pose refinement and learn to approximate the rasterization backward pass in differentiable rendering from data. In particular, we introduce a novel network architecture that jointly performs both tasks. Our network maps real-world images and synthetic renderings to a common feature space and predicts deep cross-domain correspondences in the form of geometric correspondence fields (see Fig. 1, middle). Geometric correspondence fields hold 2D displacement vectors between corresponding 2D object points in RGB images and 3D model renderings similar to optical flow [5]. These predicted 2D displacement vectors serve as pixel-level gradients that enable us to approximate the rasterization backward pass and compute accurate gradients for renderer inputs like the 3D pose, the 3D model, or the camera intrinsics that minimize an ideal geometric reprojection loss.
Our approach has three main advantages: First, we can leverage depth, normal, and object coordinate [2] renderings which provide 3D pose information more explicitly than RGB and mask renderings [23]. Second, we avoid task-irrelevant appearance variations in the RGB space and 3D pose ambiguities in the mask space [9]. Third, we learn to approximate the rasterization backward pass from data instead of relying on a hand-crafted algorithm [14, 17, 27].
To demonstrate the benefits of our novel 3D pose refinement approach, we evaluate it on the challenging Pix3D [39] dataset. We present quantitative as well as qualitative results and significantly outperform state-of-the-art refinement methods in multiple metrics by up 55% relative. Finally, we combine our refinement approach with feed-forward 3D pose estimation [8] and 3D model retrieval [9] methods to predict fine-grained 3D poses for objects in the wild without providing initial 3D poses or ground truth 3D models at runtime given only a single RGB image. To summarize, our main contributions are:
-
We introduce the first refinement method based on differentiable rendering that does not compare real-world images and synthetic renderings in the RGB or mask space but in a feature space optimized for the task at hand.
-
We present a novel differentiable renderer that learns to approximate the rasterization backward pass instead of relying on a hand-crafted algorithm.
2 Related Work
In the following, we discuss prior work on differentiable rendering, 3D pose estimation, and 3D pose refinement.
2.1 Differentiable Rendering
Differentiable rendering [27] is a powerful concept that provides inverse graphics capabilities by computing gradients for 3D scene parameters from 2D image observations. This novel technique recently gained popularity for 3D reconstruction [20, 33], scene lighting estimation [1, 22], and texture prediction [16, 49].
However, rendering is a non-differentiable process due to the rasterization operation [17]. Thus, differentiable rendering approaches either try to mimic rasterization with differentiable operations [26, 34] or use conventional rasterization and approximate its backward pass [6, 14, 45].
In this work, we also approximate the rasterization backward pass but, in contrast to existing methods, do not rely on hand-crafted approximations. Instead, we train a network that performs the approximation. This idea is not only applicable for 3D pose estimation but also for other tasks like 3D reconstruction, human pose estimation, or the prediction of camera intrinsics in the future.
2.2 3D Pose Estimation
Modern 3D pose estimation approaches build on deep feed-forward networks and can be divided into two groups: Direct and correspondence-based methods.
Direct methods predict 3D pose parameters as raw network outputs. They use classification [41, 42], regression [30, 46], or hybrid variants of both [28, 48] to estimate 3D rotation and 3D translation [21, 31, 32] in an end-to-end manner. Recent approaches additionally integrate these techniques into detection pipelines to deal with multiple objects in a single image [18, 20, 44, 47].
In contrast, correspondence-based methods predict keypoint locations and recover 3D poses from 2D-3D correspondences using PnP algorithms [36, 38] or trained shape models [35]. In this context, different methods predict sparse object-specific keypoints [35,36,37], sparse virtual control points [7, 38, 40], or dense unsupervised 2D-3D correspondences [2, 3, 8, 15, 43].
In this work, we use the correspondence-based feed-forward approach presented in [8] to predict initial 3D poses for refinement.
2.3 3D Pose Refinement
3D pose refinement methods are based on the assumption that the projection of an object’s 3D model aligns with the object’s appearance in the image given the correct 3D pose. Thus, they compare renderings under the current 3D pose to the input image to get feedback on the prediction.
A simple approach to refine 3D poses is to generate many small perturbations and evaluate their accuracy using a scoring function [25, 50]. However, this is computationally expensive and the design of the scoring function is unclear. Therefore, other approaches try to predict iterative 3D pose updates with deep networks instead [23, 29, 38, 52]. In practice, though, the performance of these methods is limited because they cannot generalize to 3D poses or 3D models that have not been seen during training [38].
Recent approaches based on differentiable rendering overcome these limitations [17, 27, 34]. Compared to the methods described above, they analytically propagate error signals backward through the rendering pipeline to compute more accurate 3D pose updates. In this way, they exploit knowledge about the 3D scene geometry and the projection pipeline for the optimization.
In contrast to existing differentiable rendering approaches that rely on comparisons in the RGB [27] or mask [17, 34] space, we compare RGB images and 3D model renderings in a feature space that is optimized for 3D pose refinement.
3 Learned 3D Pose Refinement
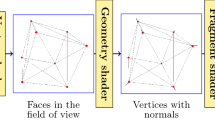
Given a single RGB image, a 3D model, and an initial 3D pose, we compute iterative updates to refine the 3D pose, as shown in Fig. 2. For this purpose, we first introduce the objective function that we optimize at runtime (see Sect. 3.1). We then explain how we compare the input RGB image to renderings under the current 3D pose in a feature space optimized for refinement (see Sect. 3.2), predict pixel-level gradients that minimize an ideal geometric reprojection loss in the form of geometric correspondence fields (see Sect. 3.3), and propagate gradients backward through the rendering pipeline to perform a gradient-based optimization directly on the 3D pose (see Sect. 3.4).
Overview of our system. In the forward pass ( ), we generate 3D model renderings under the current 3D pose. In the backward pass (
), we generate 3D model renderings under the current 3D pose. In the backward pass ( ), we map the RGB image and our renderings to a common feature space and predict a geometric correspondence field that enables us to approximate the rasterization backward pass and compute gradients for the 3D pose that minimize an ideal geometric reprojection loss. (Color figure online)
), we map the RGB image and our renderings to a common feature space and predict a geometric correspondence field that enables us to approximate the rasterization backward pass and compute gradients for the 3D pose that minimize an ideal geometric reprojection loss. (Color figure online)
3.1 Runtime Object Function
Our approach to refine the 3D pose of an object is based on the numeric optimization of an objective function at runtime. In particular, we seek to minimize an ideal geometric reprojection loss
for all provided 3D model vertices \(\mathbf {M}_i\). In this case, \(\text {proj}(\cdot )\) performs the projection from 3D space to the 2D image plane, \(\mathcal {P}\) denotes the 3D pose parameters, and \(\mathcal {P}_\text {gt}\) is the ground truth 3D pose. Hence, it is clear that \(\mathrm {argmin}e(\mathcal {P}) = \mathcal {P}_\text {gt}\).
To efficiently minimize \(e(\mathcal {P})\) using a gradient-based optimization starting from an initial 3D pose, we compute gradients for the 3D pose using the Jacobian of \(e(\mathcal {P})\) with respect to \(\mathcal {P}\). Applying the chain rule yields the expression

where \(\mathcal {P}_\text {curr}\) is the current 3D pose estimate and the point where the Jacobian is evaluated. In this case, the term \(\left[ \frac{\partial \text {proj}(\mathbf {M}_i,\mathcal {P})}{\partial \mathcal {P}}\right] ^T\) can be computed analytically because it is simply a sequence of differentiable operations. In contrast, the term \(\big [\text {proj}(\mathbf {M}_i, \mathcal {P}_\text {gt}) - \text {proj}(\mathbf {M}_i, \mathcal {P}_\text {curr})\big ]\) cannot be computed analytically because the 3D model vertices projected under the ground truth 3D pose, i.e., \(\text {proj}(\mathbf {M}_i, \mathcal {P}_\text {gt})\), are unknown at runtime and can only be observed indirectly via the input image.
However, for visible vertices, this term can be calculated given a geometric correspondence field (see Sect. 3.4). Thus, we introduce a novel network architecture that learns to predict geometric correspondence fields given an RGB image and 3D model renderings under the current 3D pose estimate in the following. Moreover, we embed this network in a differentiable rendering framework to approximate the rasterization backward pass and compute gradients for renderer inputs like the 3D pose of an object in an end-to-end manner (see Fig. 2).
3.2 Refinement Feature Space
The first step in our approach is to render the provided 3D model under the current 3D pose using the forward pass of our differentiable renderer (see Fig. 2). In particular, we generate depth, normal, and object coordinate [2] renderings. These representations provide 3D pose and 3D shape information more explicitly than RGB or mask renderings which makes them particularly useful for 3D pose refinement [9]. By concatenating the different renderings along the channel dimension, we leverage complementary information from different representations in the backward pass rather than relying on a single type of rendering [27].
Next, we begin the backward pass of our differentiable renderer by mapping the input RGB image and our multi-representation renderings to a common feature space. For this task, we use two different network branches that bridge the domain gap between the real and rendered images (see Fig. 2). Our mapping branches use a custom architecture based on task-specific design choices:
First, we want to predict local cross-domain correspondences under the assumption that the initial 3D pose is close to the ground truth 3D pose. Thus, we do not require features with global context but features with local discriminability. For this reason, we use small fully convolutional networks which are fast, memory-efficient, and learn low-level features that generalize well across different objects. Because the low-level structures appearing across different objects are similar, we do not require a different network for each object [38] but address objects of all categories with a single class-agnostic network for each domain.
Second, we want to predict correspondences with maximum spatial accuracy. Thus, we do not use pooling or downsampling but maintain the spatial resolution throughout the network. In this configuration, consecutive convolutions provide sufficient receptive field to learn advanced shape features which are superior to simple edge intensities [18], while higher layers benefit from full spatial parameter sharing during training which increases generalization. As a consequence, the effective minibatch size during training is higher than the number of images per minibatch because only a subset of all image pixels contributes to each computed feature. In addition, the resulting high spatial resolution feature space provides an optimal foundation for computing spatially accurate correspondences.
For the implementation of our mapping branches, we use fully convolutional networks consisting of an initial \(7\times 7\) Conv-BN-ReLU block, followed by three residual blocks [12, 13], and a \(1\times 1\) Conv-BN-ReLU block for dimensionality reduction. This architecture enforces local discriminability and high spatial resolution and maps RGB images and multi-representation renderings to \(W\times H\times 64\) feature maps, where W and H are the spatial dimensions of the input image.
3.3 Geometric Correspondence Fields
After mapping RGB images and 3D model renderings to a common feature space, we compare their feature maps and predict cross-domain correspondences. For this purpose, we concatenate their feature maps and use another fully convolutional network branch to predict correspondences, as shown in Fig. 2.
In particular, we regress per-pixel correspondence vectors in the form of geometric correspondence fields (see Fig. 1, middle). Geometric correspondence fields hold 2D displacement vectors between corresponding 2D object points in real-world RGB images and synthetic 3D model renderings similar to optical flow [5]. These displacement vectors represent the projected relative 2D motion of individual 2D object points that is required to minimize the reprojection error and refine the 3D pose. A geometric correspondence field has the same spatial resolution as the respective input RGB image and two channels, i.e., \(W\times H\times 2\).
If an object’s 3D model and 3D pose are known, we can render the ground truth geometric correspondence field for an arbitrary 3D pose. For this task, we first compute the 2D displacement \(\nabla \mathbf {m}_i = \text {proj}(\mathbf {M}_i,\mathcal {P}_\text {gt}) - \text {proj}(\mathbf {M}_i,\mathcal {P}_\text {curr})\) between the projection under the ground truth 3D pose \(\mathcal {P}_\text {gt}\) and the current 3D pose \(\mathcal {P}_\text {curr}\) for each 3D model vertex \(\mathbf {M}_i\). We then generate a ground truth geometric correspondence field \(G(\mathcal {P}_\text {curr},\mathcal {P}_\text {gt})\) by rendering the 3D model using a shader that interpolates the per-vertex 2D displacements \(\nabla \mathbf {m}_i\) across the projected triangle surfaces using barycentric coordinates.
In our scenario, predicting correspondences using a network has two advantages compared to traditional correspondence matching [10]. First, predicting correspondences with convolutional kernels is significantly faster than exhaustive feature matching during both training and testing [51]. This is especially important in the case of dense correspondences. Second, training explicit correspondences can easily result in degenerated feature spaces and requires tedious regularization and hard negative sample mining [4].
For the implementation of our correspondence branch, we use three consecutive \(7\times 7\) Conv-BN-ReLU blocks followed by a final \(7\times 7\) convolution which reduces the channel dimensionality to two. For this network, a large receptive field is crucial to cover correspondences with high spatial displacement.
However, in many cases local correspondence prediction is ambiguous. For example, many objects are untextured and have homogeneous surfaces, e.g., the backrest and the seating surface of the chair in Fig. 1, which cause unreliable correspondence predictions. To address this problem, we additionally employ a geometric attention module which restricts the correspondence prediction to visible object regions with significant geometric discontinuities, as outlined in white underneath the 2D displacement vectors in Fig. 1. We identify these regions by finding local variations in our renderings.
In particular, we detect rendering-specific intensity changes larger than a certain threshold within a local \(5\times 5\) window to construct a geometric attention mask \(w^{att}\). For each pixel of \(w^{att}\), we compute the geometric attention weight
In this case, \(R(\mathcal {P}_\text {curr})\) is a concatenation of depth, normal, and object coordinate renderings under the current 3D pose \(\mathcal {P}_\text {curr}\), (x, y) is a pixel location, and (u, v) are pixel offsets within the window W. The comparison function \(\delta ^R(\cdot )\) and the threshold \(t^R\) are different for each type of rendering. For depth renderings, we compute the absolute difference between normalized depth values and use a threshold of 0.1. For normal renderings, we compute the angle between normals and use a threshold of \(15^\circ \). For object coordinate renderings, we compute the Euclidean distance between 3D points and use a threshold of 0.1. If any of these thresholds applies, the corresponding pixel (x, y) in our geometric attention mask \(w^{att}\) becomes active. Because we already generated these renderings before, our geometric attention mechanism requires almost no additional computations and is available during both training and testing.
Training. During training of our system, we optimize the learnable part of our differentiable renderer, i.e., a joint network \(f(\cdot )\) consisting of our two mapping branches and our correspondence branch with parameters \(\theta \) (see Fig. 2). Formally, we minimize the error between predicted \(f(\cdot )\) and ground truth \(G(\cdot )\) geometric correspondence fields as
In this case, \(w^{att}\) is a geometric attention mask, I is an RGB image, \(R(\mathcal {P}_\text {curr})\) is a concatenation of depth, normal, and object coordinate renderings generated under a random 3D pose \(\mathcal {P}_\text {curr}\) produced by perturbing the ground truth 3D pose \(\mathcal {P}_\text {gt}\), \(G(\mathcal {P}_\text {curr},\mathcal {P}_\text {gt})\) is the ground truth geometric correspondence field, and (x, y) is a pixel location. In particular, we first generate a random 3D pose \(\mathcal {P}_\text {curr}\) around the ground truth 3D pose \(\mathcal {P}_\text {gt}\) for each training sample in each iteration. For this purpose, we sample 3D pose perturbations from normal distributions and apply them to \(\mathcal {P}_\text {gt}\) to generate \(\mathcal {P}_\text {curr}\). For 3D rotations, we use absolute perturbations with \(\sigma =5^\circ \). For 3D translations, we use relative perturbations with \(\sigma =0.1\). We then render the ground truth geometric correspondence field \(G(\mathcal {P}_\text {curr},\mathcal {P}_\text {gt})\) between the perturbed 3D pose \(\mathcal {P}_\text {curr}\) and the ground truth 3D pose \(\mathcal {P}_\text {gt}\) as described above, generate concatenated depth, normal, and object coordinate renderings \(R(\mathcal {P}_\text {curr})\) under the perturbed 3D pose \(\mathcal {P}_\text {curr}\), and compute the geometric attention mask \(w^{att}\). Finally, we predict a geometric correspondence field using our network \(f(I, R(\mathcal {P}_\text {curr}); \theta )\) given the RGB image I and the renderings \(R(\mathcal {P}_\text {curr})\), and optimize for the network parameters \(\theta \).
In this way, we train a network that performs three tasks: First, it maps RGB images and multi-representation 3D model renderings to a common feature space. Second, it compares features in this space. Third, it predicts geometric correspondence fields which serve as pixel-level gradients that enable us to approximate the rasterization backward pass of our differentiable renderer.
3.4 Learned Differentiable Rendering
In the classic rendering pipeline, the only non-differentiable operation is the rasterization [27] that determines which pixels of a rendering have to be filled, solves the visibility of projected triangles, and fills the pixels using a shading computation. This discrete operation raises one main challenge: Its gradient is zero, which prevents gradient flow [17]. However, we must flow non-zero gradients from pixels to projected 3D model vertices to perform differentiable rendering.
To approximate the rasterization backward pass, we predict a geometric correspondence field (left), disperse the predicted 2D displacement of each pixel among the vertices of its corresponding visible triangle (middle), and normalize the contributions of all pixels. In this way, we obtain gradients for projected 3D model vertices (right).
We solve this problem using geometric correspondence fields. Instead of actually differentiating a loss in the image space and relying on hand-crafted comparisons between pixel intensities to approximate the gradient flow from pixels to projected 3D model vertices [14, 17], we first use a network to predict per-pixel 2D displacement vectors in the form of a geometric correspondence field, as shown in Fig. 2. We then compute gradients for projected 3D model vertices by simply accumulating the predicted 2D displacement vectors using our knowledge of the projected 3D model geometry, as illustrated in Fig. 3.
Formally, we compute the gradient of a projected 3D model vertex \(\mathbf {m}_i\) as

In this case, \(f(I, R(\mathcal {P}_\text {curr}); \theta )\) is a geometric correspondence field predicted by our network \(f(\cdot )\) with frozen parameters \(\theta \) given an RGB image I and concatenated 3D model renderings \(R(\mathcal {P}_\text {curr})\) under the current 3D pose estimate \(\mathcal {P}_\text {curr}\), \(w^{att}_{x,y}\) is a geometric attention weight, \(w^{bar,i}_{x,y}\) is a barycentric weight for \(\mathbf {m}_i\), and (x, y) is a pixel position. We accumulate predicted 2D displacement vectors for all positions (x, y) for which \(\mathbf {m}_i\) is a vertex of the triangle \(\bigtriangleup _{\texttt {IndexMap}_{x,y}}\) visible at (x, y). For this task, we generate an IndexMap which stores the index of the visible triangle for each pixel during the forward pass of our differentiable renderer.
Inference. Our computed \(\nabla \mathbf {m}_i\) approximate the second term in Eq. (2) that cannot be computed analytically. In this way, our approach combines local per-pixel 2D displacement vectors into per-vertex gradients and further computes accurate global 3D pose gradients considering the 3D model geometry and the rendering pipeline. Our experiments show that this approach generalizes better to unseen data than predicting 3D pose updates with a network [23, 52].
During inference of our system, we perform iterative updates to refine \(\mathcal {P}_\text {curr}\). In each iteration, we compute a 3D pose gradient by evaluating our refinement loop presented in Fig. 2. For our implementation, we use the Adam optimizer [19] with a small learning rate and perform multiple updates to account for noisy correspondences and achieve the best accuracy.
4 Experimental Results
To demonstrate the benefits of our 3D pose refinement approach, we evaluate it on the challenging Pix3D [39] dataset which provides in-the-wild images for objects of different categories. In particular, we quantitatively and qualitatively compare our approach to state-of-the-art refinement methods in Sect. 4.1, perform an ablation study in Sect. 4.2, and combine our refinement approach with feed-forward 3D pose estimation [8] and 3D model retrieval [9] methods to predict fine-grained 3D poses without providing initial 3D poses or ground truth 3D models in Sect. 4.3. We follow the evaluation protocol of [8] and report the median (MedErr) of rotation, translation, pose, and projection distances. Details on evaluation setup, datasets, and metrics as well as extensive results and further experiments are provided in our supplementary material.
4.1 Comparison to the State of the Art
We first quantitatively compare our approach to state-of-the-art refinement methods. For this purpose, we perform 3D pose refinement on top of an initial 3D pose estimation baseline. In particular, we predict initial 3D poses using the feed-forward approach presented in [8] which is the state of the art for single image 3D pose estimation on the Pix3D dataset (Baseline). We compare our refinement approach to traditional image-based refinement without differentiable rendering [52] (Image Refinement) and mask-based refinement with differentiable rendering [17] (Mask Refinement).
RGB-based refinement with differentiable rendering [27] is not possible in our setup because all available 3D models lack textures and materials. This approach even fails if we compare grey-scale images and renderings because the image intensities at corresponding locations do not match. As a consequence, 2D-3D alignment using a photo-metric loss is impossible.
For Image Refinement, we use grey-scale instead of RGB renderings because all available 3D models lack textures and materials. In addition, we do not perform a single full update [52] but perform up to 1000 iterative updates with a small learning rate of \(\eta = 0.05\) using the Adam optimizer [19] for all methods.
For Mask Refinement, we predict instance masks from the input RGB image using Mask R-CNN [11]. To achieve maximum accuracy, we internally predict masks at four times the original spatial resolution proposed in Mask R-CNN and fine-tune a model pre-trained on COCO [24] on Pix3D.
Table 1 (
 ) summarizes our results. In this experiment, we provide the ground truth 3D model of the object in the image for refinement. Compared to the baseline, Image Refinement only achieves a small improvement in the rotation, translation, and pose metrics. There is almost no improvement in the projection metric (\(MedErr_{P}\)), as this method does not minimize the reprojection error. Traditional refinement methods are not aware of the rendering pipeline and the underlying 3D scene geometry and can only provide coarse 3D pose updates
[52]. In our in-the-wild scenario, the number of 3D models, possible 3D pose perturbations, and category-level appearance variations is too large to simulate all permutations during training. As a consequence, this method cannot generalize to examples which are far from the ones seen during training and only achieves small improvements.
) summarizes our results. In this experiment, we provide the ground truth 3D model of the object in the image for refinement. Compared to the baseline, Image Refinement only achieves a small improvement in the rotation, translation, and pose metrics. There is almost no improvement in the projection metric (\(MedErr_{P}\)), as this method does not minimize the reprojection error. Traditional refinement methods are not aware of the rendering pipeline and the underlying 3D scene geometry and can only provide coarse 3D pose updates
[52]. In our in-the-wild scenario, the number of 3D models, possible 3D pose perturbations, and category-level appearance variations is too large to simulate all permutations during training. As a consequence, this method cannot generalize to examples which are far from the ones seen during training and only achieves small improvements.
 , our refinement significantly outperforms previous refinement methods across all metrics by up to 55% relative. In the case of automatically
, our refinement significantly outperforms previous refinement methods across all metrics by up to 55% relative. In the case of automatically
 (+ Retrieval
[9]), we reduce the 3D pose error (\(MedErr_{R,t}\)) compared to the state of the art for single image 3D pose estimation on Pix3D (Baseline) by 55% relative without using additional inputs.
(+ Retrieval
[9]), we reduce the 3D pose error (\(MedErr_{R,t}\)) compared to the state of the art for single image 3D pose estimation on Pix3D (Baseline) by 55% relative without using additional inputs.Additionally, we observe that after the first couple of refinement steps, the predicted updates are not accurate enough to refine the 3D pose but start to jitter without further improving the 3D pose. Moreover, for many objects, the prediction fails and the iterative updates cause the 3D pose to drift off. Empirically, we obtain the best overall results for this method using only 20 iterations. For all other methods based on differentiable rendering, we achieve the best accuracy after the full 1000 iterations. A detailed analysis on this issue is presented in our supplementary material.
Next, Mask Refinement improves upon Image Refinement by a large margin across all metrics. Due to the 2D-3D alignment with differentiable rendering, this method computes more accurate 3D pose updates and additionally reduces the reprojection error (\(MedErr_{P}\)). However, we observe that Mask Refinement fails in two common situations: First, when the object has holes and the mask is not a single blob the refinement fails (see Fig. 5, e.g., 1st row - right example). In the presence of holes, the hand-crafted approximation for the rasterization backward pass accumulates gradients with alternating signs while traversing the image. This results in unreliable per-vertex motion gradients. Second, simply aligning the silhouette of objects is ambiguous as renderings under different 3D poses can have similar masks. The interior structure of the object is completely ignored. As a consequence, the refinement gets stuck in poor local minima. Finally, the performance of Mask Refinement is limited by the quality of the target mask predicted from the RGB input image [11].
Qualitative 3D pose refinement results for objects of different categories. We project the ground truth 3D model on the image using the 3D pose estimated by different methods. Our approach overcomes the limitations of previous methods and predicts fine-grained 3D poses for objects in the wild. The last example shows a failure case (indicated by the
 ) where the initial 3D pose is too far from the ground truth 3D pose and no refinement method can converge. More qualitative results are presented in our supplementary material. Best viewed in digital zoom. (Color figure online)
) where the initial 3D pose is too far from the ground truth 3D pose and no refinement method can converge. More qualitative results are presented in our supplementary material. Best viewed in digital zoom. (Color figure online)
In contrast, our refinement overcomes these limitations and significantly outperforms the baseline as well as competing refinement methods across all metrics by up to 70% and 55% relative. Using our geometric correspondence fields, we bridge the domain gap between real-world images and synthetic renderings and align both the object outline as well as interior structures with high accuracy.
Our approach performs especially well in the fine-grained regime, as shown in Fig. 4a. In this experiment, we plot the 3D pose accuracy \(Acc_{R,t}\) which gives the percentage of samples for which the 3D pose distance \(e_{R,t}\) is smaller than a varying threshold. For strict thresholds close to zero, our approach outperforms other refinement methods by a large margin. For example, at the threshold 0.015, we achieve more than 55% accuracy while the runner-up Mask Refinement achieves only 19% accuracy.
This significant performance improvement is also reflected in our qualitative examples presented in Fig. 5. Our approach precisely aligns 3D models to objects in RGB images and computes 3D poses which are in many cases visually indistinguishable from the ground truth. Even if the initial 3D pose estimate (Baseline) is significantly off, our method can converge towards the correct 3D pose (see Fig. 5, e.g., 1st row - left example). Finally, Fig. 6 illustrates the high quality of our predicted geometric correspondence fields.
4.2 Ablation Study
To understand the importance of individual components in our system, we conduct an ablation study in Table 2. For this purpose, we modify a specific system component, retrain our approach, and evaluate the performance impact.
If we use smaller kernels with less receptive field (\(3\times 3\) vs \(7\times 7\)) or fewer layers (2 vs 4) in our correspondence branch, the performance drops significantly. Also, using shallow mapping branches which only employ a single Conv-BN-ReLU block to simulate simple edge and ridge features results in low accuracy because the computed features are not discriminative enough. If we perform refinement without our geometric attention mechanism, the accuracy degrades due to unreliable correspondence predictions in homogeneous regions.
Next, the choice of the rendered representation is important for the performance of our approach. While using masks only performs poorly, depth, normal, and object coordinate renderings increase the accuracy. Finally, we achieve the best accuracy by exploiting complementary information from multiple different renderings by concatenating depth, normal, and object coordinate renderings.
By inspecting failure cases, we observe that our method does not converge if the initial 3D pose is too far from the ground truth 3D pose (see Fig. 5, last example). In this case, we cannot predict accurate correspondences because our computed features are not robust to large viewpoint changes and the receptive field of our correspondence branch is limited. In addition, occlusions cause our refinement to fail because there are no explicit mechanisms to address them. We plan to resolve this issue in the future by predicting occlusion masks and correspondence confidences. However, other refinement methods also fail in these scenarios (see Fig. 5, last example).
4.3 3D Model Retrieval
So far, we assumed that the ground truth 3D model required for 3D pose refinement is given at runtime. However, we can overcome this limitation by automatically retrieving 3D models from single RGB images. For this purpose, we combine all refinement approaches with the retrieval method presented in [9], where the 3D model database essentially becomes a part of the trained model. In this way, we perform initial 3D pose estimation, 3D model retrieval, and 3D pose refinement given only a single RGB image. This setting allows us to benchmark refinement methods against feed-forward baselines in a fair comparison.
The corresponding results are presented in Table 1 (
 ) and Fig. 4b. Because the retrieved 3D models often differ from the ground truth 3D models, the refinement performance decreases compared to given ground truth 3D models. Differentiable rendering methods lose more accuracy than traditional refinement methods because they require 3D models with accurate geometry.
) and Fig. 4b. Because the retrieved 3D models often differ from the ground truth 3D models, the refinement performance decreases compared to given ground truth 3D models. Differentiable rendering methods lose more accuracy than traditional refinement methods because they require 3D models with accurate geometry.
Still, all refinement approaches perform remarkably well with retrieved 3D models. As long as the retrieved 3D model is reasonably close to the ground truth 3D model in terms of geometry, our refinement succeeds. Our method achieves even lower 3D pose error (\(MedErr_{R,t}\)) with retrieved 3D models than Mask Refinement with ground truth 3D models. Finally, using our joint 3D pose estimation-retrieval-refinement pipeline, we reduce the 3D pose error (\(MedErr_{R,t}\)) compared to the state of the art for single image 3D pose estimation on Pix3D (Baseline) by 55% relative without using additional inputs.
5 Conclusion
Aligning 3D models to objects in RGB images is the most accurate way to predict 3D poses. However, there is a domain gap between real-world images and synthetic renderings which makes this alignment challenging in practice. To address this problem, we predict deep cross-domain correspondences in a feature space optimized for 3D pose refinement and combine local 2D displacement vectors into global 3D pose updates using our novel differentiable renderer. Our method outperforms existing refinement approaches by up to 55% relative and can be combined with feed-forward 3D pose estimation and 3D model retrieval to predict fine-grained 3D poses for objects in the wild given only a single RGB image. Finally, our novel learned differentiable rendering framework can be used for other tasks in the future.
References
Azinovic, D., Li, T.M., Kaplanyan, A., Niessner, M.: Inverse path tracing for joint material and lighting estimation. In: Conference on Computer Vision and Pattern Recognition, pp. 2447–2456 (2019)
Brachmann, E., Krull, A., Michel, F., Gumhold, S., Shotton, J., Rother, C.: Learning 6D object pose estimation using 3D object coordinates. In: Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T. (eds.) ECCV 2014. LNCS, vol. 8690, pp. 536–551. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-319-10605-2_35
Brachmann, E., Michel, F., Krull, A., Ying Yang, M., Gumhold, S., Rother, C.: Uncertainty-driven 6D pose estimation of objects and scenes from a single RGB image. In: Conference on Computer Vision and Pattern Recognition, pp. 3364–3372 (2016)
Choy, C.B., Gwak, J., Savarese, S., Chandraker, M.: Universal correspondence network. In: Advances in Neural Information Processing Systems, pp. 2414–2422 (2016)
Dosovitskiy, A., et al.: FlowNet: learning optical flow with convolutional networks. In: Conference on Computer Vision and Pattern Recognition, pp. 2758–2766 (2015)
Genova, K., Cole, F., Maschinot, A., Sarna, A., Vlasic, D., Freeman, W.T.: Unsupervised training for 3D morphable model regression. In: Conference on Computer Vision and Pattern Recognition, pp. 8377–8386 (2018)
Grabner, A., Roth, P.M., Lepetit, V.: 3D pose estimation and 3D model retrieval for objects in the wild. In: Conference on Computer Vision and Pattern Recognition, pp. 3022–3031 (2018)
Grabner, A., Roth, P.M., Lepetit, V.: GP2C: geometric projection parameter consensus for joint 3D pose and focal length estimation in the wild. In: International Conference on Computer Vision, pp. 2222–2231 (2019)
Grabner, A., Roth, P.M., Lepetit, V.: Location field descriptors: single image 3D model retrieval in the wild. In: International Conference on 3D Vision, pp. 583–593 (2019)
Hartley, R., Zisserman, A.: Multiple View Geometry in Computer Vision. Cambridge University Press, Cambridge (2003)
He, K., Gkioxari, G., Dollár, P., Girshick, R.: Mask R-CNN. In: International Conference on Computer Vision, pp. 2980–2988 (2017)
He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: Conference on Computer Vision and Pattern Recognition, pp. 770–778 (2016)
He, K., Zhang, X., Ren, S., Sun, J.: Identity mappings in deep residual networks. In: Leibe, B., Matas, J., Sebe, N., Welling, M. (eds.) ECCV 2016. LNCS, vol. 9908, pp. 630–645. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-319-46493-0_38
Henderson, P., Ferrari, V.: Learning to generate and reconstruct 3D meshes with only 2D supervision. In: British Machine Vision Conference, pp. 139:1–139:13 (2018)
Jafari, O.H., Mustikovela, S.K., Pertsch, K., Brachmann, E., Rother, C.: iPose: instance-aware 6D pose estimation of partly occluded objects. In: Jawahar, C., Li, H., Mori, G., Schindler, K. (eds.) ACCV 2018. LNCS, vol. 11363, pp. 477–492. SPringer, Heidelberg (2018). https://doi.org/10.1007/978-3-030-20893-6_30
Kanazawa, A., Tulsiani, S., Efros, A.A., Malik, J.: Learning category-specific mesh reconstruction from image collections. In: European Conference on Computer Vision, pp. 371–386 (2018)
Kato, H., Ushiku, Y., Harada, T.: Neural 3D mesh renderer. In: Conference on Computer Vision and Pattern Recognition, pp. 3907–3916 (2018)
Kehl, W., Manhardt, F., Tombari, F., Ilic, S., Navab, N.: SSD-6D: making RGB-based 3D detection and 6D pose estimation great again. in: International Conference on Computer Vision, pp. 1530–1538 (2017)
Kingma, D.P., Ba, J.: Adam: a method for stochastic optimization. arXiv:1412.6980 (2014)
Kundu, A., Li, Y., Rehg, J.M.: 3D-RCNN: instance-level 3D object reconstruction via render-and-compare. In: Conference on Computer Vision and Pattern Recognition, pp. 3559–3568 (2018)
Li, C., Bai, J., Hager, G.D.: A unified framework for multi-view multi-class object pose estimation. In: European Conference on Computer Vision, pp. 1–16 (2018)
Li, T.M., Aittala, M., Durand, F., Lehtinen, J.: Differentiable Monte Carlo ray tracing through edge sampling. In: ACM SIGGRAPH Asia, pp. 222:1–222:11 (2018)
Li, Y., Wang, G., Ji, X., Xiang, Y., Fox, D.: DeepIM: deep iterative matching for 6D pose estimation. In: European Conference on Computer Vision, pp. 683–698 (2018)
Lin, T.Y., et al.: Microsoft COCO: common objects in context. In: Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T. (eds.) ECCV 2014. LNCS, vol. 8693, pp. 740–755. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-319-10602-1_48
Liu, L., Lu, J., Xu, C., Tian, Q., Zhou, J.: Deep fitting degree scoring network for monocular 3D object detection. In: Conference on Computer Vision and Pattern Recognition, pp. 1057–1066 (2019)
Liu, S., Li, T., Chen, W., Li, H.: Soft rasterizer: a differentiable renderer for image-based 3D reasoning. In: International Conference on Computer Vision, pp. 7708–7717 (2019)
Loper, M.M., Black, M.J.: OpenDR: an approximate differentiable renderer. In: Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T. (eds.) ECCV 2014. LNCS, vol. 8695, pp. 154–169. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-319-10584-0_11
Mahendran, S., Ali, H., Vidal, R.: A mixed classification-regression framework for 3D pose estimation from 2D images. In: British Machine Vision Conference, pp. 238:1–238:12 (2018)
Manhardt, F., Kehl, W., Navab, N., Tombari, F.: Deep model-based 6D pose refinement in RGB. In: European Conference on Computer Vision, pp. 800–815 (2018)
Massa, F., Marlet, R., Aubry, M.: Crafting a multi-task CNN for viewpoint estimation. In: British Machine Vision Conference, pp. 91:1–91:12 (2016)
Mottaghi, R., Xiang, Y., Savarese, S.: A coarse-to-fine model for 3D pose estimation and sub-category recognition. In: Conference on Computer Vision and Pattern Recognition, pp. 418–426 (2015)
Mousavian, A., Anguelov, D., Flynn, J., Kosecka, J.: 3D bounding box estimation using deep learning and geometry. In: Conference on Computer Vision and Pattern Recognition, pp. 7074–7082 (2017)
Nguyen-Phuoc, T.H., Li, C., Balaban, S., Yang, Y.: RenderNet: a deep convolutional network for differentiable rendering from 3D shapes. In: Advances in Neural Information Processing Systems, pp. 7891–7901 (2018)
Palazzi, A., Bergamini, L., Calderara, S., Cucchiara, R.: End-to-end 6-DoF object pose estimation through differentiable rasterization. In: European Conference on Computer Vision Workshops, pp. 1–14 (2018)
Pavlakos, G., Zhou, X., Chan, A., Derpanis, K., Daniilidis, K.: 6-DoF object pose from semantic keypoints. In: International Conference on Robotics and Automation, pp. 2011–2018 (2017)
Peng, S., Liu, Y., Huang, Q., Zhou, X., Bao, H.: 3D object class detection in the wild. In: Conference on Computer Vision and Pattern Recognition, pp. 4561–4570 (2019)
Pepik, B., Stark, M., Gehler, P., Ritschel, T., Schiele, B.: 3D object class detection in the wild. In: Conference on Computer Vision and Pattern Recognition Workshops, pp. 1–10 (2015)
Rad, M., Lepetit, V.: BB8: a scalable, accurate, robust to partial occlusion method for predicting the 3D poses of challenging objects without using depth. In: International Conference on Computer Vision, pp. 3828–3836 (2017)
Sun, X., et al.: Pix3D: dataset and methods for single-image 3D shape modeling. In: Conference on Computer Vision and Pattern Recognition, pp. 2974–2983 (2018)
Tekin, B., Sinha, S.N., Fua, P.: Real-time seamless single shot 6D object pose prediction. In: Conference on Computer Vision and Pattern Recognition, pp. 292–301 (2018)
Tulsiani, S., Carreira, J., Malik, J.: Pose induction for novel object categories. In: International Conference on Computer Vision, pp. 64–72 (2015)
Tulsiani, S., Malik, J.: Viewpoints and keypoints. In: Conference on Computer Vision and Pattern Recognition, pp. 1510–1519 (2015)
Wang, H., Sridhar, S., Huang, J., Valentin, J., Song, S., Guibas, L.: Normalized object coordinate space for category-level 6D object pose and size estimation. In: Conference on Computer Vision and Pattern Recognition, pp. 2642–2651 (2019)
Wang, Y., et al.: 3D pose estimation for fine-grained object categories. In: European Conference on Computer Vision Workshops (2018)
Wu, J., Zhang, C., Xue, T., Freeman, W.T., Tenenbaum, J.: Learning a probabilistic latent space of object shapes via 3D generative-adversarial modeling. In: Advances in Neural Information Processing Systems, pp. 82–90 (2016)
Xiang, Y., et al.: ObjectNet3D: a large scale database for 3D object recognition. In: Leibe, B., Matas, J., Sebe, N., Welling, M. (eds.) ECCV 2016. LNCS, vol. 9912, pp. 160–176. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-319-46484-8_10
Xiang, Y., Schmidt, T., Narayanan, V., Fox, D.: PoseCNN: a convolutional neural network for 6D object pose estimation in cluttered scenes. In: Robotics: Science and Systems Conference, pp. 1–10 (2018)
Xiao, Y., Qiu, X., Langlois, P.A., Aubry, M., Marlet, R.: Pose from shape: deep pose estimation for arbitrary 3D objects. In: British Machine Vision Conference, pp. 120:1–120:14 (2019)
Yao, S., Hsu, T.M., Zhu, J.Y., Wu, J., Torralba, A., Freeman, W.T., Tenenbaum, J.: 3D-Aware Scene Manipulation via Inverse Graphics. In: Advances in Neural Information Processing Systems. pp. 1887–1898 (2018)
Zabulis, X., Lourakis, M.I.A., Stefanou, S.S.: 3D pose refinement using rendering and texture-based matching. In: International Conference on Computer Vision and Graphics, pp. 672–679 (2014)
Zagoruyko, S., Komodakis, N.: Learning to compare image patches via convolutional neural networks. In: Conference on Computer Vision and Pattern Recognition, pp. 4353–4361 (2015)
Zakharov, S., Shugurov, I., Ilic, S.: DPOD: dense 6D pose object detector in RGB images. In: International Conference on Computer Vision, pp. 1941–1950 (2019)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
1 Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Grabner, A. et al. (2020). Geometric Correspondence Fields: Learned Differentiable Rendering for 3D Pose Refinement in the Wild. In: Vedaldi, A., Bischof, H., Brox, T., Frahm, JM. (eds) Computer Vision – ECCV 2020. ECCV 2020. Lecture Notes in Computer Science(), vol 12361. Springer, Cham. https://doi.org/10.1007/978-3-030-58517-4_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-58517-4_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-58516-7
Online ISBN: 978-3-030-58517-4
eBook Packages: Computer ScienceComputer Science (R0)