Skip to main content
Springer Nature Link
Log in

Numbers of Served and Lost Customers in Busy-Periods of M/M/1/n Systems with Balking

  • Conference paper
  • First Online:
Computational Science and Its Applications – ICCSA 2020 (ICCSA 2020)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 12251))

Included in the following conference series:

  • 1630 Accesses

Abstract

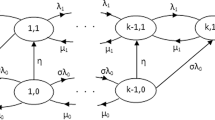
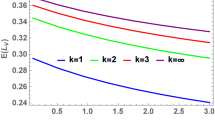
In this work we analyze single server Markovian queueing systems with finite capacity and balking, that is M/M/1/n systems with balking. In these systems, the admission of customers is modulated by the state of the system at the instants of customer arrivals. Depending on the size of the queue upon arrival, customers that find place to join the system decide to enter the system with a certain probability. The number of customers in the system amounts to a Markov chain whose transition probabilities incorporate the balking probabilities. Using the Markovian regenerative property of the chain embedded at the instants of arrival or departure of customers, we characterize the joint probability distribution of the number of customers served and the number of customers lost in busy-periods, that is, during continuous occupation periods of the server. This is accomplished implementing a priori a recursive algorithmic procedure for computing the respective probability-generating function. Finally, a numerical illustration of the derived results is presented for different balking policies.

This research was partially supported by Fundação para a Ciência e a Tecnologia (FCT) through project UID/Multi/04621/2019.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Al Hanbali, A.: Busy period analysis of the level dependent \(PH/PH/1/K\) queue. Queueing Syst. 67(3), 221–249 (2011). https://doi.org/10.1007/s11134-011-9213-6

    Article  MathSciNet  MATH  Google Scholar 

  2. Ancker, C.J., Gafarian, A.V.: Some queuing problems with balking and reneging II. Oper. Res. 11(6), 928–937 (1963)

    Article  MathSciNet  Google Scholar 

  3. Ferreira, F., Pacheco, A.: Analysis of \(GI^X/M(n)//N\) systems with stochastic customer acceptance policy. Queueing Syst. 58, 29–55 (2008). https://doi.org/10.1007/s11134-007-9057-2

    Article  MathSciNet  MATH  Google Scholar 

  4. Guha, D., Goswami, V., Banik, A.D.: Algorithmic computation of steady-state probabilities in an almost observable \(GI/M/c\) queue with or without vacations under state dependent balking and reneging. Appl. Math. Model. 40, 4199–4219 (2016)

    Article  MathSciNet  Google Scholar 

  5. Haight, F.A.: Queuing with balking I. Biometriika 44(3–4), 360–369 (1957)

    Article  MathSciNet  Google Scholar 

  6. Harris, T.J.: The remaining busy period of a finite queue. Oper. Res. 19, 219–223 (1971)

    Article  Google Scholar 

  7. Jain, N.K., Kumar, R., Som, B.K.: An \(M/M/1/N\) queuing system with reverse balking. Am. J. Oper. Res. 4(2), 17–20 (2014)

    Google Scholar 

  8. Kumar, R., Sharma, S.: Transient analysis of an \(M/M/c\) queuing system with balking and retention of reneging customers. Commun. Stat. Theory Methods 47(6), 1318–1327 (2018)

    Article  MathSciNet  Google Scholar 

  9. Kumar, R., Som, B.K.: An \(M/M/1/N\) queuing system with reverse balking and reverse reneging. AMO-Adv. Model. Optim. 16(2), 339–353 (2014)

    MATH  Google Scholar 

  10. Laxmi, P.V., Gupta, U.C.: Analysis of finite-buffer multi-server queues with group arrivals: \(GI^X/M/c/N\). Queueing Syst. 36(1–3), 125–140 (2000). https://doi.org/10.1023/A:1019179119172

    Article  MATH  Google Scholar 

  11. Peköz, E.A., Righter, R., Xia, C.H.: Characterizing losses during busy periods in finite buffer systems. J. Appl. Probab. 40(1), 242–249 (2003)

    Article  MathSciNet  Google Scholar 

  12. Som, B.K., Kumar, R.: A heterogeneous queuing system with reverse balking and reneging. J. Ind. Prod. Eng. 35(1), 1–5 (2018)

    Google Scholar 

  13. Wang, K., Li, N., Jiang, Z.: Queuing system with impatient customers: a review. In: IEEE International Conference on Service Operations and Logistics and Informatics, 15–17 July 2010, Shandong, pp. 82–87 (2010)

    Google Scholar 

  14. Wang, Q., Zhang, B.: Analysis of a busy period queuing system with balking, reneging and motivating. Appl. Math. Model. 64, 480–488 (2018)

    Article  MathSciNet  Google Scholar 

  15. Yue, D., Zhang, Y., Yue, W.: Optimal performance analysis of an \(M/M/1/N\) queue system with balking, reneging and server vacation. Int. J. Pure Appl. Math. 28, 101–115 (2006)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Trás-os-Montes and Alto Douro, Vila Real, Portugal

    Fátima Ferreira

  2. Instituto Superior Técnico, Universidade de Lisboa, Lisbon, Portugal

    António Pacheco

  3. Escola Superior de Tecnologia e Gestão do Politécnico de Leiria, Leiria, Portugal

    Helena Ribeiro

  4. CEMAT, Instituto Superior Técnico, Universidade de Lisboa, Lisbon, Portugal

    Fátima Ferreira, António Pacheco & Helena Ribeiro

Authors
  1. Fátima Ferreira
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. António Pacheco
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Helena Ribeiro
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Helena Ribeiro .

Editor information

Editors and Affiliations

  1. University of Perugia, Perugia, Italy

    Osvaldo Gervasi

  2. University of Basilicata, Potenza, Potenza, Italy

    Beniamino Murgante

  3. Chair- Center of ICT/ICE, Covenant University, Ota, Nigeria

    Sanjay Misra

  4. University of Cagliari, Cagliari, Italy

    Chiara Garau

  5. University of Cagliari, Cagliari, Italy

    Ivan Blečić

  6. Clayton School of Information Technology, Monash University, Clayton, VIC, Australia

    David Taniar

  7. Department of Information Science, Kyushu Sangyo University, Fukuoka, Japan

    Bernady O. Apduhan

  8. University of Minho, Braga, Portugal

    Ana Maria A. C. Rocha

  9. Polytechnic University of Bari, Bari, Italy

    Eufemia Tarantino

  10. Polytechnic University of Bari, Bari, Italy

    Carmelo Maria Torre

  11. Department of Neurology, University of Massachusetts Medical School, Worcester, MA, USA

    Yeliz Karaca

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Ferreira, F., Pacheco, A., Ribeiro, H. (2020). Numbers of Served and Lost Customers in Busy-Periods of M/M/1/n Systems with Balking. In: Gervasi, O., et al. Computational Science and Its Applications – ICCSA 2020. ICCSA 2020. Lecture Notes in Computer Science(), vol 12251. Springer, Cham. https://doi.org/10.1007/978-3-030-58808-3_12

Download citation

  • DOI: https://doi.org/10.1007/978-3-030-58808-3_12

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-030-58807-6

  • Online ISBN: 978-3-030-58808-3

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics