Abstract
This paper explores the power of catalytic computation when the catalytic space (c(n), the full memory for which the content needs to be restored to original content at the end of the computation) is much more than exponential in the pure space (s(n), the empty memory which does not have any access/restoration constraints). We study the following three regimes of the relation between s(n) and c(n) and explore the class \(\mathsf {CSPACE}(s(n),c(n))\) in each of them.
-
Low-end regime : \(s(n) = O(1)\) We define the classes \(\mathsf {CR}\) and \(\mathsf {CNR}\) (nondeterministic variant of \(\mathsf {CR}\)) where \(s(n)=O(1)\) and
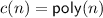 . Exploring the connection between computational power of one counter machines (OC) and constant pure space catalytic Turing machines, we observe that \(\mathsf {OC}\subseteq \mathsf {CR}\) and show that \(\mathsf {CR}\subseteq \mathsf {OC}\implies \mathsf {CR}\ne \mathsf {CNR}\). We prove that \(\mathsf {L}\not \subseteq \mathsf {CSPACE}(O(1), o(\sqrt{n}))\)
. Exploring the connection between computational power of one counter machines (OC) and constant pure space catalytic Turing machines, we observe that \(\mathsf {OC}\subseteq \mathsf {CR}\) and show that \(\mathsf {CR}\subseteq \mathsf {OC}\implies \mathsf {CR}\ne \mathsf {CNR}\). We prove that \(\mathsf {L}\not \subseteq \mathsf {CSPACE}(O(1), o(\sqrt{n}))\) -
Low-end non-constant regime: \(s(n) = o(\log \log n)\): Let M be an oblivious catalytic Turing machine using s(n) pure space and c(n) catalytic space such that \(s(n) + \log c(n) = o(\log \log n)\) then L(M) is regular. This strengthens the classical theorem on \(s(n) = o(\log \log n)\) to the case of catalytic Turing machines.
-
High-end regime: \(s(n) = O(c(n)^\epsilon )\): We show an implementation of incremental dynamic program using catalytic machines, thus showing that Knapsack problem (with n items, sum of their costs as C and the capacity of the bag as K) can be solved in \(O(n\log n\log C+\log (nKC))\) pure space and \(O(n^2KC^3\log ^2 K \log n)\) catalytic space. Hence, catalytic algorithms can lead to a non-trivial saving in the pure space required for computation when K is \(\varOmega (n)\).
Our techniques include interesting generalizations of crossing sequence arguments and implementations of incremental dynamic programs using catalytic algorithms. These may be of independent interest.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
See Sect. 2 for a formal definition.
- 2.
The class of languages that can be computed by uniform Boolean circuits of depth \(O(\log n)\) and size \(O(n^k)\) for a constant k, over \(\{\mathsf {MAJ}, \lnot \}\) gates.
- 3.
- 4.
Holds since \(N^1(f_n) \ge n\) and \(R_0^{pub}(f_n) = \varOmega (N^1(f_n)- \log n)\). See Chap. 3 of [7] for details.
References
Buhrman, H., Cleve, R., Koucký, M., Loff, B., Speelman, F.: Computing with a full memory: catalytic space. STOC 2014, 857–866 (2014)
Buhrman, H., Koucký, M., Loff, B., Speelman, F.: Catalytic space: non-determinism and hierarchy. Theory Comput. Syst. 62(1), 116–135 (2018). https://doi.org/10.1007/s00224-017-9784-7
Duris, P., Galil, Z.: Fooling a two way automaton or one pushdown store is better than one counter for two way machines. Theor. Comput. Sci. 21, 39–53 (1982)
Jukna, S.: Limitations of incremental dynamic programming. Algorithmica 69(2), 461–492 (2014). https://doi.org/10.1007/s00453-013-9747-6
Koucký, M.: Catalytic computation. Bull. EATCS 118 (2016)
Kozen, D.: Theory of Computation. Texts in Computer Science. Springer, London (2006). https://doi.org/10.1007/1-84628-477-5
Kushilevitz, E., Nisan, N.: Communication Complexity. Cambridge University Press, Cambridge (1997)
Acknowledgments
The authors thank the anonymous reviewers for their constructive comments. Part of the work was done while the second author was at IIT Madras and was supported by the ERP funding CSE1718842RFERMNJA.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Bisoyi, S., Dinesh, K., Sarma, J. (2020). On Pure Space vs Catalytic Space. In: Chen, J., Feng, Q., Xu, J. (eds) Theory and Applications of Models of Computation. TAMC 2020. Lecture Notes in Computer Science(), vol 12337. Springer, Cham. https://doi.org/10.1007/978-3-030-59267-7_37
Download citation
DOI: https://doi.org/10.1007/978-3-030-59267-7_37
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-59266-0
Online ISBN: 978-3-030-59267-7
eBook Packages: Computer ScienceComputer Science (R0)


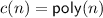 . Exploring the connection between computational power of one counter machines (OC) and constant pure space catalytic Turing machines, we observe that
. Exploring the connection between computational power of one counter machines (OC) and constant pure space catalytic Turing machines, we observe that