Abstract
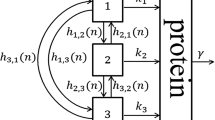
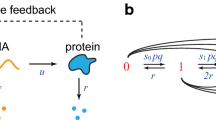
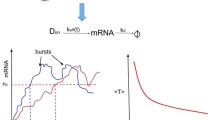
Regulatory molecules such as transcription factors are often present at relatively small copy numbers in living cells. The copy number of a particular molecule fluctuates in time due to the random occurrence of production and degradation reactions. Here we consider a stochastic model for a self-regulating transcription factor whose lifespan (or time till degradation) follows a general distribution modelled as per a multi-dimensional phase-type process. We show that at steady state the protein copy-number distribution is the same as in a one-dimensional model with exponentially distributed lifetimes. This invariance result holds only if molecules are produced one at a time: we provide explicit counterexamples in the bursty production regime. Additionally, we consider the case of a bistable genetic switch constituted by a positively autoregulating transcription factor. The switch alternately resides in states of up- and downregulation and generates bimodal protein distributions. In the context of our invariance result, we investigate how the choice of lifetime distribution affects the rates of metastable transitions between the two modes of the distribution. The phase-type model, being non-linear and multi-dimensional whilst possessing an explicit stationary distribution, provides a valuable test example for exploring dynamics in complex biological systems.
CÇ is supported by the Comenius University grant for doctoral students Nos. UK/201/2019 and UK/106/2020. PB is supported by the Slovak Research and Development Agency under the contract No. APVV-18-0308, by the VEGA grant 1/0347/18, and the EraCoSysMed project 4D-Healing. AS is supported by the National Science Foundation grant ECCS-1711548 and ARO W911NF-19-1-0243.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Abel, J.H., Drawert, B., Hellander, A., Petzold, L.R.: GillesPy: a python package for stochastic model building and simulation. IEEE Life Sci. Lett. 2(3), 35–38 (2017)
Alon, U.: An Introduction to Systems Biology: Design Principles of Biological Circuits. Chapman & Hall/CRC (2007)
Andreychenko, A., Bortolussi, L., Grima, R., Thomas, P., Wolf, V.: Distribution approximations for the chemical master equation: comparison of the method of moments and the system size expansion. In: Graw, F., Matthäus, F., Pahle, J. (eds.) Modeling Cellular Systems. CMCS, vol. 11, pp. 39–66. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-45833-5_2
Backenköhler, M., Bortolussi, L., Wolf, V.: Control variates for stochastic simulation of chemical reaction networks. In: Bortolussi, L., Sanguinetti, G. (eds.) CMSB 2019. LNCS, vol. 11773, pp. 42–59. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-31304-3_3
Becskei, A., Séraphin, B., Serrano, L.: Positive feedback in eukaryotic gene networks: cell differentiation by graded to binary response conversion. EMBO J. 20, 2528–2535 (2001)
Blake, W., Kaern, M., Cantor, C., Collins, J.: Noise in eukaryotic gene expression. Nature 422, 633–637 (2003)
Bokes, P., Lin, Y., Singh, A.: High cooperativity in negative feedback can amplify noisy gene expression. Bull. Math. Biol. 80, 1871–1899 (2018)
Bokes, P.: Postponing production exponentially enhances the molecular memory of a stochastic switch. BioRxiv (2020). https://doi.org/10.1101/2020.06.19.160754
Bokes, P., Borri, A., Palumbo, P., Singh, A.: Mixture with delayed distributions in a stochastic gene expression model feedback: a WKB approximation approach. J. Math. Biol. 81(1), 343–367 (2020). https://doi.org/10.1007/s00285-020-01512-y
Bokes, P., Hojcka, M., Singh, A.: Buffering gene expression noise by MicroRNA based feedforward regulation. In: Češka, M., Šafránek, D. (eds.) CMSB 2018. LNCS, vol. 11095, pp. 129–145. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-99429-1_8
Bokes, P., King, J.R., Wood, A.T., Loose, M.: Exact and approximate distributions of protein and mRNA levels in the low-copy regime of gene expression. J. Math. Biol. 64, 829–854 (2012). https://doi.org/10.1007/s00285-011-0433-5
Bokes, P., Singh, A.: Controlling noisy expression through auto regulation of burst frequency and protein stability. In: Češka, M., Paoletti, N. (eds.) HSB 2019. LNCS, vol. 11705, pp. 80–97. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-28042-0_6
Bortolussi, L., Lanciani, R., Nenzi, L.: Model checking Markov population models by stochastic approximations. Inf. Comput. 262, 189–220 (2018)
Bratsun, D., Volfson, D., Tsimring, L.S., Hasty, J.: Delay-induced stochastic oscillations in gene regulation. Proc. Natl. Acad. Sci. U.S.A. 102(41), 14593–14598 (2005)
Cai, L., Friedman, N., Xie, X.: Stochastic protein expression in individual cells at the single molecule level. Nature 440, 358–362 (2006)
Cinquemani, E.: Identifiability and reconstruction of biochemical reaction networks from population snapshot data. Processes 6(9), 136 (2018)
Cinquemani, E.: Stochastic reaction networks with input processes: analysis and application to gene expression inference. Automatica 101, 150–156 (2019)
Dar, R.D., Razooky, B.S., Singh, A., Trimeloni, T.V., McCollum, J.M., Cox, C.D., Simpson, M.L., Weinberger, L.S.: Transcriptional burst frequency and burst size are equally modulated across the human genome. Proc. Natl. Acad. Sci. U.S.A. 109, 17454–17459 (2012)
Deneke, C., Lipowsky, R., Valleriani, A.: Complex degradation processes lead to non-exponential decay patterns and age-dependent decay rates of messenger RNA. PLoS ONE 8(2), e55442 (2013)
Escudero, C., Kamenev, A.: Switching rates of multistep reactions. Phys. Rev. E 79(4), 041149 (2009)
Friedman, N., Cai, L., Xie, X.: Linking stochastic dynamics to population distribution: an analytical framework of gene expression. Phys. Rev. Lett. 97, 168302 (2006)
Griffith, J.: Mathematics of cellular control processes II. Positive feedback to one gene. J. Theor. Biol. 20(2), 209–216 (1968)
Gross, D.: Fundamentals of Queueing Theory. Wiley, Hoboken (2008)
Guet, C., Henzinger, T.A., Igler, C., Petrov, T., Sezgin, A.: Transient memory in gene regulation. In: Bortolussi, L., Sanguinetti, G. (eds.) CMSB 2019. LNCS, vol. 11773, pp. 155–187. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-31304-3_9
Hanggi, P., Grabert, H., Talkner, P., Thomas, H.: Bistable systems: master equation versus Fokker-Planck modeling. Phys. Rev. A 29(1), 371 (1984)
Hinch, R., Chapman, S.J.: Exponentially slow transitions on a Markov chain: the frequency of calcium sparks. Eur. J. Appl. Math. 16(04), 427–446 (2005)
Innocentini, G.C.P., Antoneli, F., Hodgkinson, A., Radulescu, O.: Effective computational methods for hybrid stochastic gene networks. In: Bortolussi, L., Sanguinetti, G. (eds.) CMSB 2019. LNCS, vol. 11773, pp. 60–77. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-31304-3_4
Innocentini, G.C., Hodgkinson, A., Radulescu, O.: Time dependent stochastic mRNA and protein synthesis in piecewise-deterministic models of gene networks. Front. Phys. 6, 46 (2018)
Jackson, J.R.: Jobshop-like queueing systems. Manage. Sci. 10(1), 131–142 (1963)
Jia, T., Kulkarni, R.: Intrinsic noise in stochastic models of gene expression with molecular memory and bursting. Phys. Rev. Lett. 106(5), 58102 (2011)
Johnson, N., Kotz, S., Kemp, A.: Univariate Discrete Distributions, 3rd edn. Wiley, Hoboken (2005)
van Kampen, N.: Stochastic Processes in Physics and Chemistry. Elsevier, Amsterdam (2006)
Kelly, F.P.: Reversibility and Stochastic Networks. Cambridge University Press, Cambridge (2011)
Kendall, D.: Stochastic processes and population growth. J. Roy. Stat. Soc. B 11, 230–282 (1949)
Kurasov, P., Lück, A., Mugnolo, D., Wolf, V.: Stochastic hybrid models of gene regulatory networks - a PDE approach. Math. Biosci. 305, 170–177 (2018)
Lagershausen, S.: Performance Analysis of Closed Queueing Networks, vol. 663. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32214-3
Lestas, I., Paulsson, J., Ross, N., Vinnicombe, G.: Noise in gene regulatory networks. IEEE Trans. Circ. I 53(1), 189–200 (2008)
Liu, L., Kashyap, B., Templeton, J.: On the \({GI}^{X}/{G}/\infty \) system. J. Appl. Probab. 27(3), 671–683 (1990)
McShane, E., Sin, C., Zauber, H., Wells, J.N., Donnelly, N., Wang, X., Hou, J., Chen, W., Storchova, Z., Marsh, J.A., et al.: Kinetic analysis of protein stability reveals age-dependent degradation. Cell 167(3), 803–815 (2016)
Miȩkisz, J., Poleszczuk, J., Bodnar, M., Foryś, U.: Stochastic models of gene expression with delayed degradation. Bull. Math. Biol. 73(9), 2231–2247 (2011)
Michaelides, M., Hillston, J., Sanguinetti, G.: Geometric fluid approximation for general continuous-time Markov chains. Proc. Roy. Soc. A 475(2229), 20190100 (2019)
Michaelides, M., Hillston, J., Sanguinetti, G.: Statistical abstraction for multi-scale spatio-temporal systems. ACM Trans. Model. Comput. Simul. 29(4), 1–29 (2019)
Newby, J., Chapman, J.: Metastable behavior in Markov processes with internal states. Journal of Mathematical Biology 69(4), 941–976 (2013). https://doi.org/10.1007/s00285-013-0723-1
Norris, J.R.: Markov Chains. Cambridge Univ Press, Cambridge (1998)
Prajapat, M.K., Ribeiro, A.S.: Added value of autoregulation and multi-step kinetics of transcription initiation. R. Soc. Open Sci. 5(11), 181170 (2018)
Ross, S.M.: Introduction to probability models. Academic Press, Cambridge (2014)
Samal, S.S., Krishnan, J., Esfahani, A.H., Lüders, C., Weber, A., Radulescu, O.: Metastable Regimes and Tipping Points of Biochemical Networks with Potential Applications in Precision Medicine. In: Liò, P., Zuliani, P. (eds.) Automated Reasoning for Systems Biology and Medicine. CB, vol. 30, pp. 269–295. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17297-8_10
Schnoerr, D., Sanguinetti, G., Grima, R.: Approximation and inference methods for stochastic biochemical kinetics-a tutorial review. J. Phys. A: Math. Theor. 50(9), 093001 (2017)
Soltani, M., Vargas-Garcia, C.A., Antunes, D., Singh, A.: Intercellular variability in protein levels from stochastic expression and noisy cell cycle processes. PLoS Comput. Biol. 12(8), e1004972 (2016)
Taniguchi, Y., Choi, P., Li, G., Chen, H., Babu, M., Hearn, J., Emili, A., Xie, X.: Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science 329, 533–538 (2010)
Thattai, M., van Oudenaarden, A.: Intrinsic noise in gene regulatory networks. Proc. Natl. Acad. Sci. U.S.A. 98(15), 8614–8619 (2001)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Çelik, C., Bokes, P., Singh, A. (2020). Stationary Distributions and Metastable Behaviour for Self-regulating Proteins with General Lifetime Distributions. In: Abate, A., Petrov, T., Wolf, V. (eds) Computational Methods in Systems Biology. CMSB 2020. Lecture Notes in Computer Science(), vol 12314. Springer, Cham. https://doi.org/10.1007/978-3-030-60327-4_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-60327-4_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-60326-7
Online ISBN: 978-3-030-60327-4
eBook Packages: Computer ScienceComputer Science (R0)