Abstract
TotemBioNet is a new software platform to assist the design of qualitative regulatory network models by combining “genetically modified Hoare logic”, temporal logic model checking and optimized enumeration techniques. TotemBioNet is particularly efficient to manage parameter identification, the most critical step of formal modelling. It is also remarkably flexible and efficient to check properties in order to explore biological assumptions. To illustrate this efficacy, we address the classical example of the cell cycle, where the passage from one phase to the next one, called checkpoint, is crucial but is usually a rather fuzzy informal concept. The cyclic behaviour of the cell cycle is specified by temporal logic and the order of individual events inside each phase is explored thanks to quantifiers introduced in Hoare logic. This way, TotemBioNet rapidly suggests a sensible formalization of the notion of checkpoint.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Batt, G., Bergamini, D., de Jong, H., Garavel, H., Mateescu, R.: Model checking genetic regulatory networks using GNA and CADP. In: Graf, S., Mounier, L. (eds.) SPIN 2004. LNCS, vol. 2989, pp. 158–163. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24732-6_12
Behaegel, J., Comet, J.P., Bernot, G., Cornillon, E., Delaunay, F.: A hybrid model of cell cycle in mammals. J. Bioinform. Comput. Biol. 14(1), 1640001 (2016)
Bernot, G., Comet, J.P., Khalis, Z., Richard, A., Roux, O.F.: A genetically modified Hoare logic. Theor. Comput. Sci. 765, 145–157 (2019)
Bernot, G., Comet, J.P., Richard, A., Guespin, J.: Application of formal methods to biological regulatory networks: extending Thomas’ asynchronous logical approach with temporal logic. J. Theor. Biol. 229(3), 339–347 (2004)
Chabrier, N., Fages, F.: Symbolic model checking of biochemical networks. In: Priami, C. (ed.) CMSB 2003. LNCS, vol. 2602, pp. 149–162. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36481-1_13
Cimatti, A., et al.: NuSMV 2: an OpenSource tool for symbolic model checking. In: Brinksma, E., Larsen, K.G. (eds.) CAV 2002. LNCS, vol. 2404, pp. 359–364. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45657-0_29
Fages, F., Soliman, S.: On robustness computation and optimization in BIOCHAM-4. In: Češvka, M., Šafránek, D. (eds.) CMSB 2018. LNCS, vol. 11095, pp. 292–299. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-99429-1_18
Folschette, M.: The Hoare-fol tool. Technical report, Univ. Lille & CNRS UMR 9189 (2019). https://hal.archives-ouvertes.fr/hal-02409801
Guziolowski, C., et al.: Exhaustively characterizing feasible logic models of a signaling network using answer set programming. Bioinformatics 30, 1942 (2013)
Kauffman, S.A.: Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 22(3), 437–467 (1969)
Naldi, A., et al.: The CoLoMoTo interactive notebook. Front. Physiol. 9, 680 (2018)
Remy, E., Ruet, P., Mendoza, L., Thieffry, D., Chaouiya, C.: From logical regulatory graphs to standard Petri nets: dynamical roles and functionality of feedback circuits. In: Transactions on Computational Systems Biology VII, pp. 56–72 (2006)
Richard, A.: Fair Paths in CTL (2008). https://gitlab.com/totembionet/totembionet
Schwab, J., Kühlwein, S., Ikonomi, N., Kühl, M., Kestler, H.: Concepts in Boolean network modeling: what do they all mean? Comput. Struct. Biotechnol. J. 18, 571-582 (2020)
Snoussi, E.: Qualitative dynamics of a piecewise-linear differential equations: a discrete mapping approach. Dyn. Stab. Syst. 4, 189–207 (1989)
Streck, A., Thobe, K., Siebert, H.: Comparative statistical analysis of qualitative parametrization set, September 2015
Thomas, R.: Boolean formalization of genetic control circuits. J. Theor. Biol. 42(3), 563–585 (1973)
Thomas, R.: Logical analysis of systems comprising feedback loops. J. Theor. Biol. 73(4), 631–56 (1978)
Thomas, R., Gathoye, A., Lambert, L.: A complex control circuit. Regulation of immunity in temperate bacteriophages. Eur. J. Biochem. 71(1), 211–227 (1976)
Acknowledgements
We are grateful to all contributors/users: M. Folschette (Hoare-fol), S. Ndèye and E. Gallésio (antlr4 parser and installation scripts), L. Gibart (beta tests on big models). We are also indebted to A. Richard for SMBioNet and the constructive proof of translation from fair-path CTL to CTL. This work also benefited from fruitful collaborations and discussions with J. Behaegel and F. Delaunay.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix A: Static Description of the Cell Cycle Model
See Fig. 2.
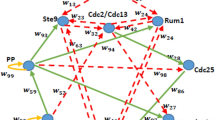
A 5-variable interaction graph of the mammalian cell cycle, from [2]. Progression through the cell cycle is driven by 2 types of genetic entities: complexes of Cyclins/Cyclin-dependant kinases (Cyc/Cdks) and their inhibitors known as ennemies. The 5 variables of the graph represent these entities, in orange. sk is the abstraction of both complexes CycE/Cdk2 and CycH/Cdk7, known as starting kinases. a and b respectively represent CycA/Cdk1 and CycB/Cdk1. en is the abstraction of the main Cyc/Cdks ennemies: the anaphase-promoting complex APC/Cdh1, cyclin-kinase inhibitors p21 and p27, and Wee1 protein. The variable ep is the anaphase-promoting complex APC/Cdc20, which is a Cyc/Cdks ennemy involved in mitosis exit and so-called exit protein. Regulations between variables are described in [2]. This interaction graph was designed using the tool yEd (www.yworks.com/products/yed). (Color figure online)
Appendix B: Equivalent Specification of \(H_{init}\) using a Fair CTL Formula
In the first experiment, the cell cycle is specified by the \(H_{init}\) Hoare triple. Here, the cell cycle is specified by the \(\varphi _{init}\) CTL formula depicting the \(H_{init}\) path.

Appendix C: Specification of \(H_{perm}\)
This Hoare triple encodes a cell cycle in which phases are described by all permutations of their respective transitions. G1 is specified in blue, S in red, G2 in grey and M in green.

Appendix D: Specification of \(H_{permG1}\)
This Hoare triple describes the cell cycle in which G1 in addition to G2 allows all permutations of its transitions.

Appendix E: Specification of \(\varphi _{G1/S}\) with CTL
The premise \(G1_{init}\) of the formula \(\varphi _{G1/S}\) is the precondition of the Hoare triple \(H_{init}\) defined in [2]. It defines the initial state of G1. The first transition of S, \(a+\), must not occur before any G1 transition. Thus 9 paths must not exist starting from the first G1 state encoded in premise.
The notation \(EX(a=1 \wedge EX(sk=1 \wedge EX(en=0 \wedge EX(sk=2))\) is a CTL version of the Hoare path: \(a+; sk+; en-; sk+\).

Appendix F: Specification and Checking of S/G2 and M/G1 Checkpoints with CTL
The premise of \(\varphi _{S/G2}\) formula (see below) encodes the first state of S. \(a-\) and \(ep+\) are the 2 possible first events of G2 according to \(H_{permG1}\). They must not occur before completion of S events. Thus 21 paths must not exist starting from the state in premise. \(\varphi _{S/G2}\) is then defined as:

Similarly, the premise of \(\varphi _{M/G1}\) formula (see below) encodes the first state of M. \(sk+\) and \(en-\) are the 2 possible first events of G1 according to \(H_{permG1}\). Thus the 8 paths enabling these events to occur before completion of M events must not exist, starting from the state in premise. \(\varphi _{M/G1}\) is then defined as:

TotemBioNet extracts no model (Table 2) for each of these checkpoints, from which we conclude that the model is not precise enough to capture them.
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Boyenval, D., Bernot, G., Collavizza, H., Comet, JP. (2020). What is a Cell Cycle Checkpoint? The TotemBioNet Answer. In: Abate, A., Petrov, T., Wolf, V. (eds) Computational Methods in Systems Biology. CMSB 2020. Lecture Notes in Computer Science(), vol 12314. Springer, Cham. https://doi.org/10.1007/978-3-030-60327-4_21
Download citation
DOI: https://doi.org/10.1007/978-3-030-60327-4_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-60326-7
Online ISBN: 978-3-030-60327-4
eBook Packages: Computer ScienceComputer Science (R0)