Abstract
The “Bright Illumination” attack [Lydersen et al., Nat. Photon. 4, 686–689 (2010)] is a practical attack, fully implementable against quantum key distribution systems. In contrast to almost all developments in quantum information processing (for example, Shor’s factorization algorithm, quantum teleportation, Bennett-Brassard (BB84) quantum key distribution, the “Photon-Number Splitting” attack, and many other examples), for which theory has been proposed decades before a proper implementation, the “Bright Illumination” attack preceded any sign or hint of a theoretical prediction. Here we explain how the “Reversed-Space” methodology of attacks, complementary to the notion of “quantum side-channel attacks” (which is analogous to a similar term in “classical”—namely, non-quantum—computer security), has missed the opportunity of predicting the “Bright Illumination” attack.
The work of T.M. and R.L. was partly supported by the Israeli MOD Research and Technology Unit, and by the Gerald Schwartz & Heather Reisman Foundation.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
The notations
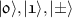 are used for the standard qubit (in a two-dimensional Hilbert space).
are used for the standard qubit (in a two-dimensional Hilbert space).
References
Bennett, C.H., Bessette, F., Brassard, G., Salvail, L., Smolin, J.: Experimental quantum cryptography. J. Cryptol. 5(1), 3–28 (1992). https://doi.org/10.1007/BF00191318
Bennett, C.H., Brassard, G.: Quantum cryptography: public key distribution and coin tossing. In: International Conference on Computers, Systems & Signal Processing, pp. 175–179 (1984)
Bennett, C.H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A., Wootters, W.K.: Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993). https://doi.org/10.1103/PhysRevLett.70.1895
Boyer, M., Gelles, R., Mor, T.: Attacks on fixed-apparatus quantum-key-distribution schemes. Phys. Rev. A 90, 012329 (2014). https://doi.org/10.1103/PhysRevA.90.012329
Brassard, G., Lütkenhaus, N., Mor, T., Sanders, B.C.: Limitations on practical quantum cryptography. Phys. Rev. Lett. 85, 1330–1333 (2000). https://doi.org/10.1103/PhysRevLett.85.1330
Brassard, G., Lütkenhaus, N., Mor, T., Sanders, B.C.: Security aspects of practical quantum cryptography. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 289–299. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_20
Deutsch, D.: Quantum theory, the Church-Turing principle and the universal quantum computer. P. Roy. Soc. Lond. A Mat. 400, 97–117 (1985). https://doi.org/10.1098/rspa.1985.0070
Gelles, R.: On the security of theoretical and realistic quantum key distribution schemes. Master’s thesis, Technion - Israel Institute of Technology, Haifa, Israel (2008)
Gelles, R., Mor, T.: Quantum-space attacks. arXiv preprint arXiv:0711.3019 (2007)
Gelles, R., Mor, T.: Reversed space attacks. arXiv preprint arXiv:1110.6573 (2011)
Gelles, R., Mor, T.: On the security of interferometric quantum key distribution. In: Dediu, A.-H., Martín-Vide, C., Truthe, B. (eds.) TPNC 2012. LNCS, vol. 7505, pp. 133–146. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33860-1_12
Gottesman, D., Lo, H.K., Lütkenhaus, N., Preskill, J.: Security of quantum key distribution with imperfect devices. Quantum Inf. Comput. 4, 325–360 (2004)
Hwang, W.Y.: Quantum key distribution with high loss: toward global secure communication. Phys. Rev. Lett. 91, 057901 (2003). https://doi.org/10.1103/PhysRevLett.91.057901
Köpf, B., Basin, D.: An information-theoretic model for adaptive side-channel attacks. In: Proceedings of the 14th ACM Conference on Computer and Communications Security, CCS 2007, pp. 286–296 (2007)
Kurtsiefer, C., et al.: A step towards global key distribution. Nature 419, 450 (2002). https://doi.org/10.1038/419450a
Lo, H.K., Curty, M., Tamaki, K.: Secure quantum key distribution. Nat. Photon. 8, 595–604 (2014). https://doi.org/10.1038/nphoton.2014.14910.1038/nphoton.2014.149
Lo, H.K., Ma, X., Chen, K.: Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005). https://doi.org/10.1103/PhysRevLett.94.230504
Lydersen, L., Wiechers, C., Wittmann, C., Elser, D., Skaar, J., Makarov, V.: Hacking commercial quantum cryptography systems by tailored bright illumination. Nat. Photon. 4, 686–689 (2010). https://doi.org/10.1038/nphoton.2010.214
Makarov, V., Anisimov, A., Skaar, J.: Effects of detector efficiency mismatch on security of quantum cryptosystems. Phys. Rev. A 74, 022313 (2006). https://doi.org/10.1103/PhysRevA.74.022313
Makarov, V., Hjelme, D.R.: Faked states attack on quantum cryptosystems. J. Mod. Opt. 52, 691–705 (2005). https://doi.org/10.1080/09500340410001730986
Pfaff, W., et al.: Unconditional quantum teleportation between distant solid-state quantum bits. Science 345, 532–535 (2014). https://doi.org/10.1126/science.1253512
Preskill, J.: Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018)
Scarani, V., Acín, A., Ribordy, G., Gisin, N.: Quantum cryptography protocols robust against photon number splitting attacks for weak laser pulse implementations. Phys. Rev. Lett. 92, 057901 (2004). https://doi.org/10.1103/PhysRevLett.92.057901
Scarani, V., Bechmann-Pasquinucci, H., Cerf, N.J., Dušek, M., Lütkenhaus, N., Peev, M.: The security of practical quantum key distribution. Rev. Mod. Phys. 81, 1301–1350 (2009). https://doi.org/10.1103/RevModPhys.81.1301
Scarani, V., Kurtsiefer, C.: The black paper of quantum cryptography: real implementation problems. Theor. Comput. Sci. 560, 27–32 (2014). https://doi.org/10.1016/j.tcs.2014.09.01510.1016/j.tcs.2014.09.015
Shamir, A.: Personal communication (around 1996–1999)
Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings 35th Annual Symposium on Foundations of Computer Science, pp. 124–134 (1994)
Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41, 303–332 (1999). https://doi.org/10.1137/S0036144598347011
Vakhitov, A., Makarov, V., Hjelme, D.R.: Large pulse attack as a method of conventional optical eavesdropping in quantum cryptography. J. Mod. Opt. 48, 2023–2038 (2001). https://doi.org/10.1080/09500340108240904
Wang, X.B.: Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94, 230503 (2005). https://doi.org/10.1103/PhysRevLett.94.230503
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Liss, R., Mor, T. (2020). From Practice to Theory: The “Bright Illumination” Attack on Quantum Key Distribution Systems. In: Martín-Vide, C., Vega-Rodríguez, M.A., Yang, MS. (eds) Theory and Practice of Natural Computing. TPNC 2020. Lecture Notes in Computer Science(), vol 12494. Springer, Cham. https://doi.org/10.1007/978-3-030-63000-3_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-63000-3_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-62999-1
Online ISBN: 978-3-030-63000-3
eBook Packages: Computer ScienceComputer Science (R0)





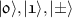 are used for the standard qubit (in a two-dimensional Hilbert space).
are used for the standard qubit (in a two-dimensional Hilbert space).