Abstract
Program watermarking enables users to embed an arbitrary string called a mark into a program while preserving the functionality of the program. Adversaries cannot remove the mark without destroying the functionality. Although there exist generic constructions of watermarking schemes for public-key cryptographic (PKC) primitives, those schemes are constructed from scratch and not efficient.
In this work, we present a general framework to equip a broad class of PKC primitives with an efficient watermarking scheme. The class consists of PKC primitives that have a canonical all-but-one (ABO) reduction. Canonical ABO reductions are standard techniques to prove selective security of PKC primitives, where adversaries must commit a target attribute at the beginning of the security game. Thus, we can obtain watermarking schemes for many existing efficient PKC schemes from standard cryptographic assumptions via our framework. Most well-known selectively secure PKC schemes have canonical ABO reductions. Notably, we can achieve watermarking for public-key encryption whose ciphertexts and secret-keys are constant-size, and that is chosen-ciphertext secure.
Our approach accommodates the canonical ABO reduction technique to the puncturable pseudorandom function (PRF) technique, which is used to achieve watermarkable PRFs. We find that canonical ABO reductions are compatible with such puncturable PRF-based watermarking schemes.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
1.1 Background
Watermarking. Watermarking enables us to embed an arbitrary string called a “mark” into a digital object such as images, videos, programs. While an embedded mark is extractable, a watermarked object should be almost functionally equivalent to the original one. Watermarking ensures that no one can remove an embedded mark without destroying the original functionality. Watermarking has two main applications. One is identifying ownership of an object. We can verify who is the original creator of objects by extracting an embedded mark that includes a unique identifier. The other is tracing malicious users that illegally copy objects. Therefore, watermarking deters unauthorized distribution.
Barak, Goldreich, Impagliazzo, Rudich, Sahai, Vadhan, and Yang initiated the study of program watermarking and gave rigorous definitions of cryptographic watermarking for programs [8]. They proved that program watermarking with perfect functionality-preserving property does not exist if there exists indistinguishability obfuscation (IO) [8]. Hopper, Molnar, and Wagner gave more definitions of cryptographic watermarking for perceptual objects and studied the relationships among them [28].
Earlier works presented watermarking schemes for specific classes of cryptographic functionalities [35, 36, 45]. However, those schemes are secure in restricted models where we limit adversary’s strategies due to the impossibility results by Barak et al. [8]. That is, earlier works [35, 36, 45] do not consider arbitrary removal strategies. Cohen, Holmgren, Nishimaki, Vaikuntanathan, and Wichs presented the first watermarking scheme for pseudorandom functions (PRFs) against arbitrary removal strategies by introducing a relaxed functionality-preserving property [19]. In addition, they observed two facts: even if we relax the functionality-preserving property, (1) we need to pick a target circuit from a distribution with high min-entropy to avoid trivial attacks in the security game. (2) learnable circuit families are not watermarkable [19]. These two facts are the reasons why most studies on cryptographic watermarking [12, 19, 22, 32, 33, 38, 44] focus on cryptographic primitives rather than arbitrary circuits.
We focus on achieving secure watermarking for public-key cryptographic primitives against arbitrary removal strategies in this study since public-key primitives are more versatile than secret-key ones.
Why Watermarking Public-Key Primitives?: An Application. Cohen et al. [19] presented an application of watermarked PRFs to electronic locks for cars. A car contains a PRF F and can only be opened by running a typical challenge-response identification protocol. A car owner has a software key (e.g., a smart-phone application) that includes a marked PRF. We can embed some identifying information to PRFs. No one can remove the owner’s information without losing the ability to unlock the car. Therefore, we can identify the car owner even if the software key is copied and the car is stolen (license plates can be forged). However, an automobile manufacturer can know user keys in this scenario since they are hard-coded in cars.Footnote 1
If we can independently generate a key pair (public and secret-keys) of a public-key primitive from the watermarking setup, then an automobile manufacturer installs the public key to a car and need not know the secret-key. Therefore, we can run a typical challenge-response protocol by watermarkable public-key encryption (PKE) or signature without revealing secret-keys to manufacturers.Footnote 2
Watermarking from Scratch or Retrofit. Goyal, Kim, Manohar, Waters, and Wu [22] presented the first feasibility result of watermarkable public-key cryptographic primitives from standard assumptions. This is an excellent work on general constructions of watermarkable public-key cryptographic primitives. However, their constructions of cryptographic primitives are built from scratch. Many efficient public-key cryptographic schemes (without watermarking functionalities) have been already proposed. One natural question is whether we can equip existing public-key cryptographic schemes with watermarking functionalities. If it is possible, we can obtain many efficient watermarkable cryptographic primitives. Our main question in this study is as follows.
Is there any general framework to equip public-key cryptographic schemes with watermarking functionalities?
We affirmatively answer to this question in this paper.
1.2 Our Contribution
We present a general framework to equip a broad class of public-key primitives with watermarking functionalities. The features of our watermarking schemes are as follows. Our watermarking schemes:
-
almost preserve the efficiency of the original public-key primitives.
-
apply to various primitives such as signature, PKE, key encapsulation mechanism (KEM), identity-based encryption (IBE), attribute-based encryption (ABE), inner-product encryption (IPE), predicate encryption (PE).
-
are secure under the same assumptions as ones used in the original public-key primitives (i.e., CDH, decisional linear (DLIN), DBDH, short integer solution (SIS), LWE assumptions, and more).
-
are independent of the original public-key primitives. (We do not need watermarking parameters to setup public-key primitives.)
-
use simulation algorithms in security reductions of the original primitives.
More details of our watermarking schemes are explained in Sect. 1.4. We will explain our technique in Sect. 1.3.
Our primary advantages are: (1) semi-general applicability, that is, we can use many existing public-key schemes almost as they are. We do not need to construct watermarkable public-key schemes from scratch. (2) achieving CCA security for PKE. (3) efficiency based on concrete cryptographic assumptions. (See the comparison in Table 1.) Those are obtained from our framework using simulation algorithms.
Using Proof Techniques as Real Algorithms. Our construction technique significantly deviates from those of previous works. The most notable feature of our result is that we present a general method to use simulation algorithms that appear in reduction-based proofs as real cryptographic algorithms. Although our study is not the first study that uses simulation algorithms to achieve new cryptographic functionalities [29, 30, 36],Footnote 3 we present the first systematic approach using simulation algorithms in real schemes. We abstract a commonly used proof technique and show that if a public-key cryptographic scheme is proven to be secure via the proof technique, we can use simulation algorithms in the reduction as watermarked cryptographic functionalities. See Sect. 1.3 for the detail. This approach enables us to equip existing schemes with watermarking functionalities.
Terminology. Before we give a technical overview, we more formally explain watermarking. A watermarking scheme consists of three algorithms called setup, marking, and extraction algorithms. A setup algorithm \(\mathsf {Setup}\) generates a marking key \(\mathsf {wmk}\) and extraction key \(\mathsf {wxk}\). A marking algorithm \(\mathsf {Mark}\) takes as input \(\mathsf {wmk}\), a circuit C, and a message \(\omega \), and outputs a marked circuit \(\widetilde{C}\). Here, \(\widetilde{C}\) should output the same output by C for most inputs. An extraction algorithm \(\mathsf {Extract}\) takes as input \(\mathsf {wxk}\) and circuit \(C'\), and outputs a string \(\omega \) or special message \(\mathsf {unmarked}\). This type of watermarking is called message-embedding. If \(\mathsf {Mark}\) does not take \(\omega \) as input and \(\mathsf {Extract}\) outputs \(\mathsf {marked}\) or \(\mathsf {unmarked}\), then we call message-less watermarking. The basic security notion is unremovability, which means no adversary can construct a circuit \(C^*\) such that the functionality of \(C^*\) is almost equivalent to that of \(\widetilde{C}\), but \(\mathsf {Extract}(\mathsf {wxk},C^*)\) outputs \(\omega ^* \ne \omega \). If we can/not publish \(\mathsf {wmk}\) and \(\mathsf {wxk}\), then we call public/secret marking and public/secret extraction, respectively.
1.3 Technical Overview
We present how to equip public-key primitives that have canonical all-but-one reductionsFootnote 4 with watermarking functionalities. All-but-one (ABO) reductions are standard proof techniques to prove selective security of public-key primitives [1, 3, 9, 10, 20, 21, 25, 31, 40]. Although our technique is not fully general, that is, we cannot apply our technique to all selectively secure public-key primitives, many well-known schemes fall into the class of canonical ABO reductions, where our technique applies. Roughly speaking, our watermarked cryptographic functionalities are simulation algorithms in ABO reductions. This technique is of independent interest because we can use simulators in security reductions as real algorithms for achieving new functionalities.
Our watermarking schemes based on canonical ABO reductions are message-less. To achieve message-embedding watermarking, we need to extend (canonical) ABO reductions to (canonical) all-but-N (ABN) reductions. However, ABO reductions are simpler to explain and it is easy to upgrade ABO reductions to ABN reductions for pairing-based schemes.Footnote 5 Thus, we first explain ABO reductions.
All-but-one Reduction. An ABO reduction is a polynomial-time algorithm that solves a problem instance \(\pi \) of a hard problem \(\varPi \) by using an adversary \(\mathcal {A}\) that breaks selective security of a cryptographic primitive \(\varSigma \). To explain ABO reductions and selective security, we introduce oracles in security games.
Adversaries have access to oracles that receives queries from adversaries and returns answers in some security games. Adversaries also declare a target to attack \(\varSigma \) at some point in the security game of \(\varSigma \). We prohibit adversaries from sending a special query (or queries) that satisfies some conditions related to the target to prevent trivial attacks. We call such a special query “query on the target”. In selective security games, adversaries must declare the target at the very beginning of the game.Footnote 6
When we prove that if \(\varPi \) is hard, then \(\varSigma \) is selectively secure, we construct the following reduction \(\mathsf {R}\). After an adversary declares a target at the beginning of a selective security game, \(\mathsf {R}\) simulates a public parameter by using a problem instance of \(\varPi \) and the target and sends the public parameter to the adversary. Then, \(\mathsf {R}\) simulates answers to all queries from the adversary except the queries on the target by using the problem instance (and the target). Note that \(\mathsf {R}\) completes the simulation without (master) secret-keys of \(\varSigma \). This type of reduction is called all-but-one reductions due to the simulation manner. In other words, if there exists an ABO reduction, then there exists an oracle simulation algorithm that works for all queries except the target.
We give an example. In the selective security game of signature, an adversary \(\mathcal {A}\) declares a target message \(\mathsf {m}^*\) at the beginning of the game. Then a challenger sends a public verification-key \(\mathsf {VK}\) to \(\mathcal {A}\). After that, \(\mathcal {A}\) can send polynomially many queries (i.e., messages) and receives signatures corresponding to the queried messages (except \(\mathsf {m}^*\)). At some point, \(\mathcal {A}\) sends a challenge \((\mathsf {m}^*,\sigma ^*)\).
A typical example of ABO reductions is the security reduction of the Boneh-Boyen signature scheme [9]. The reduction (or called simulator) \(\mathsf {R}\) is given a CDH instance \(\pi = (G,G^x,G^y)\) where \(G\) is a generator of a group \(\mathbb {G}\). When the adversary \(\mathcal {A}\) declares a target \(\mathsf {m}^*\), \(\mathsf {R}\) simulates \(\mathsf {VK}\) by using \(\pi \) and \(\mathsf {m}^*\) (embedding \(\pi \) and \(\mathsf {m}^*\) into \(\mathsf {VK}\)). Next, \(\mathsf {R}\) simulates signatures \(\sigma _\mathsf {m}\) for queried message \(\mathsf {m}\) from \(\mathcal {A}\) except \(\mathsf {m}^*\). Here, \(\mathsf {R}\) implicitly embeds \(G^{xy}\) into the signing key by setting parameters carefully (note that \(\mathsf {R}\) does not have \(G^{xy}\)). Thus, if we assume \(\mathcal {A}\) breaks the signature scheme, then \(\mathsf {R}\) can extract \(G^{xy}\) from the forged signature \(\sigma ^*\) output by \(\mathcal {A}\).
Although \(\mathsf {R}\) embeds \(\mathsf {m}^*\) in \(\mathsf {VK}\), the distribution of \(\mathsf {VK}\) by \(\mathsf {R}\) is perfectly the same as the original distribution. In addition, \(\mathsf {R}\) can perfectly simulate signatures for messages except for the target message \(\mathsf {m}^*\) due to the embedding of \(\mathsf {m}^*\). For notational convention, we separate this signature simulation algorithm part as \(\mathsf {SimSign}_{\ne \mathsf {m}^*}\). That is, we can construct an algorithm \(\mathsf {SimSign}_{\ne \mathsf {m}^*}\) from \(\pi \) and \(\mathsf {m}^*\) that outputs \(\sigma _\mathsf {m}\) for input \(\mathsf {m}\) except \(\mathsf {m}^*\). This is not necessarily possible for all selectively secure schemes since \(\mathsf {R}\) might use oracle answers for simulation. Thus, we say a reduction is “canonical” if \(\mathsf {SimSign}_{\ne \mathsf {m}^*}\) does not rely on oracle answers and is described as a stateless randomized algorithm. This proof style is sometimes called puncturing proof technique [39] since \(\mathsf {m}^*\) is like a hole in the message space and the reduction has no way to generate \(\sigma _{\mathsf {m}^*}\) for \(\mathsf {m}^*\). The graphical explanation is described in Fig. 1.
Although the case of encryption is slightly different from that of signatures, we can consider similar simulation strategies for encryption. In the PKE case, there is no “attribute”, but we can use a part of a ciphertext (sometimes called tag) as an attribute (in particular, in the CCA setting).
Illustration of ABO reduction from the selective security of signature to \(\varPi \). Solid lines denote outputs by the adversary \(\mathcal {A}\) of signature. Dashed lines denote simulation by the reduction \(\mathsf {R}\). The grayed circle is the hole. Value \(\mathsf {sol}\) denotes a solution to \(\pi \).
A Hole is to Watermark. We move to explain our unified framework to achieve watermarkable public-key primitives by using canonical ABO reductions. Roughly speaking, a punctured hole in an ABO reduction works as a watermark because adversaries cannot fill the hole. More concretely, we can consider the oracle simulation part \(\mathsf {SimSign}_{\ne \mathsf {m}^*}\) of the canonical reduction \(\mathsf {R}\) as a watermarked signature generation circuit in the signature case. In addition, no adversary can recover the ability to generate \(\sigma _{\mathsf {m}^*}\) from \(\mathsf {SimSign}_{\ne \mathsf {m}^*}\) because otherwise, the adversary can break the security of the signature scheme. (The message \(\mathsf {m}^*\) is the target.)
The ABO oracle simulation algorithm \(\mathsf {SimSign}_{\ne \mathsf {m}^*}\) preserves the functionality of the signature generation circuit except for an input \(\mathsf {m}^*\). To detect whether a circuit is watermarked or not, we check whether the circuit generates a correct output for the punctured input.Footnote 7 We can check whether a signature is valid for an message or not by using its verification algorithm. If a circuit does not generate a valid output for the punctured input (i.e., the hole), then we consider it as watermarked. In almost all ABO reductions, we have efficient algorithms that check the validity of answers from oracles.
The unremovability holds as follows. We construct a reduction \(\mathsf {R}'\) that solves a problem instance \(\pi \) by using a watermarking adversary \(\mathcal {W}\). \(\mathsf {R}'\) can give \(\mathsf {SimSign}_{\ne \mathsf {m}^*}\) to \(\mathcal {W}\) since \(\mathsf {R}'\) has \(\pi \) and \(\mathsf {m}^*\).Footnote 8 Assume that \(\mathcal {W}\) can remove the watermark. That is, we assume \(\mathcal {W}\) is given \(\mathsf {SimSign}_{\ne \mathsf {m}^*}\) and generates a circuit \(\mathsf {Sign}_{=\mathsf {m}^*}\) that can generate a signature for the target \(\mathsf {m}^*\) (i.e., filling the hole). Then, \(\mathsf {R}'\) can break the security of signature. This is because \(\mathsf {Sign}_{=\mathsf {m}^*}\) yields a forgery \(\sigma ^*\) for the target \(\mathsf {m}^*\). We can extract the solution for \(\pi \) from \(\sigma ^*\) as the ABO reduction for Boneh-Boyen signature scheme.
Put it differently, the canonical ABO reduction \(\mathsf {R}(\pi )\) works as well even if we replace the adversary \(\mathcal {A}\) of a cryptographic scheme \(\varSigma \) with the adversary \(\mathcal {W}\) for watermarking, which removes the watermark. The modified reduction \(\mathsf {R}'(\pi )\) can solve \(\pi \) because the power of removing the watermark by \(\mathcal {W}\) leads to breaking the security of \(\varSigma \). Therefore, the watermarking scheme is secure if the underlying problem is hard. The graphical explanation is described as in Fig. 2.
There are a few issues in the overview above. One issue is giving the description of \(\mathsf {SimSign}_{\ne \mathsf {m}^*}\) to the adversary since it has only black-box access to the signature generation oracle in the security game. This issue is the reason why we use “canonical” ABO reductions. If ABO reductions satisfy the canonical property, then \(\mathsf {SimSign}_{\ne \mathsf {m}^*}\) does not need oracle answers from the hard problem \(\varPi \) to simulate the signature generation oracle and can be described as a stateless randomized algorithm.
Another issue is how to prepare a problem instance and randomness for simulating \(\mathsf {VK}\) in an ABO reduction. To create an ABO reduction in the real world, we need a problem instance \(\pi \). However, what we have in the real world is not a problem instance but a secret signing-key. It is easy to find that we can perfectly simulate a problem instance and randomness for reductions by using a secret key in the real world for most ABO reductions. In addition, although \(\mathsf {SimSign}_{\ne \mathsf {m}^*}\) includes randomness for simulating \(\mathsf {VK}\), this is not an issue thanks to the randomness of the problem instance \(\pi \) (i.e., secret-key in the real world). See Sects. 4 to 6 for details.
Although we gave only intuitions in this section, we formalize properties of canonical ABO reductions in Sect. 4 and prove that we can achieve watermarking from canonical ABO reductions in Sects. 5 and 6.
Extension to all-but-N Reduction. The watermarking based on ABO reductions above is message-less watermarking. To embed an arbitrary N-bit string, we need all-but-N reduction, which can simulate oracle answers except queries on N targets. Here, N is an a-priori bounded polynomial in the security parameter. We can easily extend known cryptographic primitives that have ABO reductions to ones that have all-but-N reductions by using the technique of programmable hash functions [27] for pairing-based cryptography. We also use the fully key-homomorphic technique [10] in the lattice setting or dynamic q-type assumptions [5] for the Boneh-Boyen IBE. See Sect. 4.4 for the detail.
First, we explain a reasonable but faulty idea to achieve message-embedding watermarking based on all-but-N reductions since it helps to understand our idea. We prepare N pairs of strings \(\{t^{*}_{i,b}\}_{i\in [N],b\in \{0,1\}^{}}\) as the public parameter of watermarking. To embed a message \(\omega = (\omega _1,\ldots ,\omega _N) \in \{0,1\}^{N}\), we consider an oracle simulation algorithm that can generate answers for queries except N points in  . Concretely, in the case of signature, a signature oracle simulation algorithm \(\mathsf {SimSign}_{\notin P}\) outputs a signature \(\sigma _\mathsf {m}\) for a message \(\mathsf {m}\) such that \(\mathsf {m}\notin P\).Footnote 9 To extract an embedded message from a circuit \(C'\), we run the answer checking algorithm as in the message-less scheme for each \(i \in [N]\) and \(b \in \{0,1\}^{}\). If \(C'\) outputs a valid \(\sigma _{t^{*}_{i,1}}\) for input \(t^{*}_{i,1}\) and does not output a valid \(\sigma _{t^{*}_{i,0}}\) for input \(t^{*}_{i,0}\), then we set the i-th bit of a message to 0 and vice versa.
. Concretely, in the case of signature, a signature oracle simulation algorithm \(\mathsf {SimSign}_{\notin P}\) outputs a signature \(\sigma _\mathsf {m}\) for a message \(\mathsf {m}\) such that \(\mathsf {m}\notin P\).Footnote 9 To extract an embedded message from a circuit \(C'\), we run the answer checking algorithm as in the message-less scheme for each \(i \in [N]\) and \(b \in \{0,1\}^{}\). If \(C'\) outputs a valid \(\sigma _{t^{*}_{i,1}}\) for input \(t^{*}_{i,1}\) and does not output a valid \(\sigma _{t^{*}_{i,0}}\) for input \(t^{*}_{i,0}\), then we set the i-th bit of a message to 0 and vice versa.
This construction achieves the functionality of message-embedding watermarking. However, it is not secure because the adversary knows which points should not be punctured. That is, the points in  (and P) are publicly available information. We call \(\overline{P}\) the negation of punctured points P in this section. As already observed in some watermarkable PRFs [19, 32, 38], public punctured points could hurt watermarking security. In our case, adversary can easily destroy the functionality of cryptographic primitive at any point. More concretely, the adversary can easily modify a watermarked circuit where \(t^{*}_{i,\omega _i}\) is punctured but \(t^{*}_{i,1-\omega _i}\) is not punctured into a circuit that does not work for point \(t^{*}_{i,1-\omega _i}\) too. Then, the extraction algorithm above outputs \(\bot \) for the malformed circuit since the circuit outputs \(\bot \) both for \(t^{*}_{i,0}\) and \(t^{*}_{i,1}\).
(and P) are publicly available information. We call \(\overline{P}\) the negation of punctured points P in this section. As already observed in some watermarkable PRFs [19, 32, 38], public punctured points could hurt watermarking security. In our case, adversary can easily destroy the functionality of cryptographic primitive at any point. More concretely, the adversary can easily modify a watermarked circuit where \(t^{*}_{i,\omega _i}\) is punctured but \(t^{*}_{i,1-\omega _i}\) is not punctured into a circuit that does not work for point \(t^{*}_{i,1-\omega _i}\) too. Then, the extraction algorithm above outputs \(\bot \) for the malformed circuit since the circuit outputs \(\bot \) both for \(t^{*}_{i,0}\) and \(t^{*}_{i,1}\).
To solve the issue, we generate punctured points P and its negation \(\overline{P}\) by using PRFs and hide them instead of using publicly known punctured points and its negation. This technique is commonly used in watermarkable PRFs [19, 32, 38]. We pseudo-randomly determine punctured points and its negation based on an embedded mark and the public parameter of the target master secret-key to be watermarked. Then, the adversary has no idea about the negation of punctured points \(\overline{P}\) (and P). Therefore, it is hard for the adversary to intentionally modify a watermarked circuit into a circuit that does not work for points in \(\overline{P}\). In fact, we must prepare many punctured points  and its negation
and its negation  for each bit position i and check all points to extract i-th bit of an embedded message, where T is a polynomial in the security parameter. If a circuit output \(\bot \) for all points in \(p_i\) and a correct value for at least one point in \(\overline{p}_i\), we extract \(\omega _i\) as the i-th bit. To change the i-th bit of the embedded message without recovering the original functionality, adversaries must destroy the functionality of a circuit for all points in \(\overline{p}_i\). Advesaries can indiscriminately destroy the functionality without knowing points \((p_i,\overline{p}_i)\). However, if the adversary makes a circuit that does not work for a 1/2 plus a non-negligible fraction of inputs, then we can check that the circuit is not functionally similar to the original watermarked circuit. To make a circuit that is functionally similar to the watermarked circuit, but the extraction algorithm does not output \(\omega _i\) from, all the adversary can do is recovering the functionality of the watermarked circuit at punctured points P (\(p_i\)). This event contradicts to all-but-N reductions as the case of the message-less scheme. Thus, we can achieve unremovability.
for each bit position i and check all points to extract i-th bit of an embedded message, where T is a polynomial in the security parameter. If a circuit output \(\bot \) for all points in \(p_i\) and a correct value for at least one point in \(\overline{p}_i\), we extract \(\omega _i\) as the i-th bit. To change the i-th bit of the embedded message without recovering the original functionality, adversaries must destroy the functionality of a circuit for all points in \(\overline{p}_i\). Advesaries can indiscriminately destroy the functionality without knowing points \((p_i,\overline{p}_i)\). However, if the adversary makes a circuit that does not work for a 1/2 plus a non-negligible fraction of inputs, then we can check that the circuit is not functionally similar to the original watermarked circuit. To make a circuit that is functionally similar to the watermarked circuit, but the extraction algorithm does not output \(\omega _i\) from, all the adversary can do is recovering the functionality of the watermarked circuit at punctured points P (\(p_i\)). This event contradicts to all-but-N reductions as the case of the message-less scheme. Thus, we can achieve unremovability.
Although the message-embedding scheme above is secret marking and secret extraction, it is secure even if the adversary has the oracle access to the marking and extraction oracles. See Sect. 6 for the detail.
1.4 Comparison and Related Work
In this section, we review previous works on watermarking.Footnote 10 First, we compare our watermarking schemes with the schemes by Goyal et al. [22].
Efficient Direct Constructions and Generic Constructions. Goyal et al. [22] constructed a secret marking and secret extraction watermarking scheme for ABE (GKM+ABE) from mixed functional encryption (FE) and delegatable ABE, which can be instantiated only by the LWE assumption. They also constructed a public marking and public extraction watermarking scheme for PE (GKM+PE) from (bounded collusion-resistant) hierarchical FE, which can be instantiated by any PKE. Although the LWE assumption instantiates the schemes, the constructions are inefficient since they rely on heavy tools like mixed FE and hierarchical FE even for watermarkable PKE. In particular, in their watermarkable encryption schemes, not only the public key length but also the ciphertext length depend on the length of embedded massages (and the number of collusions in the GKM+PE case). The ciphertext size of GKM+ABE and GKM+PE is huge (See Table 1). They constructed a public marking and public extraction watermarking scheme for signature (GKM+SIG) from a prefix-constrained signature, which is instantiated with OWFs. GKM+SIG scheme is relatively efficient if it is instantiated with a signature scheme based on the symmetric external Diffie-Hellman (SXDH) assumption [16] since the transformation does not incur significant overhead.Footnote 11
Our watermarking schemes can generally equip public-key primitives with watermarking functionalities if the primitives satisfy some conditions. The equipping procedure incurs only a little overhead. Although we need to modify public-key schemes so that they have \(O(\ell \lambda )\)-size master public parameters to achieve message-embedding watermarking where \(\ell \) is the mark length and \(\lambda \) is the security parameter, the size of signatures/secret-keys/ciphertexts does not change. The signatures/secret-keys/ciphertexts consist of only a few group elements if we use group-based schemes. In addition, if we use a q-type assumption, we can use the original Boneh-Boyen scheme as it is (even the master public key is constant-size). Thus, our watermarkable public-key primitives are as efficient as known efficient public-key primitives such as Boneh-Boyen IBE scheme [9]. Therefore, in the case of encryption, our schemes are more efficient than those of Goyal et al. in the asymptotic sense. See Table 1 for the efficiency comparison.
-
\(^\mathrm{{a}}\)Tag-based encryption.
-
\(^\mathrm{{b}}\)Value \(\mathsf {hk}\) and r are a hash key and randomness of a chameleon hash function.
-
\(^\mathrm{{c}}\)At least \(\ell ^7 \lambda ^7\).
-
\(^\mathrm{{d}}\)At least \(\ell ^2 \lambda ^2\) if instantiated with FE by Ananth and Vaikuntanathan [4].
-
\(^\mathrm{{e}}\)At most \(O(\lambda ^3\log ^2{\lambda })\).
Functionalities of Watermarking. In GKM+PE, GKM+SIG, and our schemes, the watermarking setup algorithms are completely separated from the key generation algorithm of public-key primitives. However, in GKM+ABE, we need the public parameter of the watermarking scheme to generate keys of public-key primitives.
Although our message-embedding scheme is secret marking and secret extraction, it is secure even if adversaries have access to marking and extraction oracles, which answer a marked circuit and an embedded mark for queried circuits, respectively. GKM+ABE is also secret marking and secret extraction and secure under the marking and extraction oracles, but the number of extraction queries is a-priori bounded. On the other hand, GKM+PE and GKM+SIG are public marking and public extraction.
Our schemes for signature/TBE/KEM/IBE and all GKM+ schemes are message-embedding watermarking, but our schemes for ABE/PE are message-less watermarking.
Watermarking User Secret-Keys v.s. Master Secret-Keys. In GKM+ABE and GKM+PE, we can watermark user secret-keys such as secret-keys for identities (resp. policies) in IBE (resp. ABE). On the other hand, in our schemes, we can watermark master secret-keys of tag-based encryption (TBE), KEM, IBE, ABE, and PE. TBE is a variant of PKE. For signature/KEM/PKE cases, there is no difference since master secret-keys are user secret-keys in these cases.
Security Level. There are several security measures. (1) Ours for TBE/KEM achieves CCA-security, but GKM+ABE and GKM+PE for PKE do not. (2) GKM+PE and GKM+SIG are adaptively secure, but GKM+ABE and ours are selectively secure in terms of public-key primitives. In terms of embedded messages, GKM+ schemes are adaptively secure, but ours are selectively secure. See Sect. 3 for selective security of watermarking. (3) All schemes are secure even if the authority of watermarking setup is corrupted. (4) Regarding the parameter on how much adversaries should preserve functionalities to succeed attacks, GKM+ schemes are better than ours. (GKM+ is \(1/{\mathrm {poly}}(\lambda )\) while ours is \(1/2 + 1/{\mathrm {poly}}(\lambda )\).) (5) We can consider three types of collusion-resistance in this study.
-
Collusion-resistance w.r.t. cryptographic primitives: In security games of cryptographic primitives, adversaries are often allowed to send queries to master secret-key based oracles that gives additional information such as signatures in the signature case and secret-keys for identities in the IBE case. We say collusion-resistant w.r.t. cryptographic primitives if cryptographic schemes are secure even in such a setting. Both GKM+SIG and our watermarking schemes for signatures are collusion-resistant w.r.t. cryptographic primitives. GKM+ABE and our watermarking schemes for encryption (IBE, ABE, and PE) are collusion-resistant w.r.t. cryptographic primitives. On the other hand, GKM+PE is bounded collusion-resistant w.r.t. cryptographic primitives, where the number of queries is a-priori bounded.
-
Collusion-resistance w.r.t. watermarkable cryptographic primitives: We say that a watermarking scheme is collusion-resistant w.r.t. watermarkable cryptographic primitives if it is unremovable even if adversaries have access to the master secret-key based oracle explained above in security games of watermarking for public-key primitives. Both GKM+SIG and our schemes for signature are collusion-resistant w.r.t. watermarkable cryptographic primitives. Our watermarking schemes for encryption (IBE, ABE, and PE) are collusion-resistant w.r.t. watermarkable cryptographic primitives, but GKM+ABE and GKM+PE schemes are not.
-
Collusion-resistance w.r.t. watermarking: We say that a watermarking scheme is collusion-resistant w.r.t. watermarking (collusion-resistant watermarking) if it is unremovable even if adversaries are given many watermarked keys for the same original key. GKM+ABE, GKM+PE, and GKM+SIG are collusion-resistant watermarking, but ours are not.
We emphasize that even if watermarking schemes do not satisfy collusion-resistance w.r.t. watermarking, they have an application to ownership identification. This is because each user can use different keys in some settings, as we can see in the application to electronic car-lock in Sect. 1.1. Moreover, collusion-resistant watermarkable encryption is essentially the same as traitor tracing (the definition by Goyal [22] for PKE implies traitor tracing).Footnote 12 In some scenarios (ownership identification), traitor tracing (and collusion-resistant watermarking) is over-engineered. Thus, watermarking without collusion-resistance w.r.t. watermarking is meaningful enough. Moreover, if we would like to use collusion-resistant watermarkable PKE, we already have traitor tracing schemes [14, 24]. If we want to trace users in public-key primitives, we can directly consider traceable primitives rather than collusion-resistant watermarkable public-key primitives.
The construction technique by Goyal et al. relies on that of traitor tracing [17, 37] to achieve collusion-resistance w.r.t. watermarking.
Summary of Comparison. We summarize watermarkable public-key primitives by Goyal et al. [22] and ours in Tables 1 and 2. PE and ABE include PKE/IBE/IPE as special cases. Notably, ours achieves CCA security for PKE. In addition, our message-embedding scheme (Ours1 in Table 2) is much more efficient than GKM+ABE and GKM+PE as we see in Table 1. In particular, the size of secret-keys and ciphertexts in our scheme does not depend on \(\ell \). If we use q-type assumption, then even the size of master public key does not depend on \(\ell \).
The disadvantages of Ours1 and Ours3 are (1) not collusion-resistant (2) secret marking/extraction (3) selective security (4) watermarking for master secret-keys (this is not a disadvantage for PKE and signature) (5) not supporting functionalities beyond IBE. We do not have a useful application of watermarking for master secret-keys in IBE/ABE/PE cases. On the other hand, all GKM+ constructions achieve collusion-resistance, watermarking for user secret keys, and support functionalities beyond IBE. GKM+PE and GKM+SIG achieve adaptive security. Although Ours2 is public marking/extraction and supports functionalities beyond IBE, it is message-less type and watermarking for master secret-keys. Therefore, GKM+ constructions and ours are incomparable.
-
\(^\mathrm{a}\)TBE and KEM.
More on Related Work. Cohen et al. gave the first positive result on program watermarking by introducing the statistical functionality-preserving property [19]. They presented public extraction message-embedding watermarkable PRFs based on IO. Subsequently, Kim and Wu [32, 33] (KW17 and KW19) and Quach, Wichs, and Zirdelis [38] (QWZ18) presented secret extraction message-embedding watermarkable PRFs based on the LWE assumption. The KW19 and QWZ18 schemes are secure against extraction oracle attacks. In addition, QWZ18 scheme is public marking. Regarding message-embedding watermarkable PRFs, KW17, KW19, and QWZ18 schemes are relatively efficient since they are based on the LWE assumption.
Baldimtsi, Kiayias, and Samari presented watermarking schemes for public-key primitives in a relaxed model, where a trusted watermarking authority generates not only watermarked keys but also unmarked keys and algorithms are stateful [7]. We do not compare their scheme because this is a weaker model.
Goyal et al. presented not only constructions but also rigorous definitions of watermarkable public-key primitives and a relaxed functionality-preserving property for watermarkable public-key primitives [22].Footnote 13
Organization. In Sect. 2, we provide basic notions. Section 3 introduces the syntax and security definitions of watermarking. Section 4 defines canonical ABO reductions and gives examples of them. In Sect. 5, we present our message-less watermarking scheme. In Sect. 6, we present our message-embedding watermarking scheme and prove its security. Due to space limitations, we omitted many contents.
2 Preliminaries
We define some notations and introduce cryptographic notions in this section.
Notations and Basic Concepts. If \(\mathcal {X}^{(b)}=\{X^{(b)}_{\lambda }\}_{\lambda \in \mathbb {N}}\) for \(b \in \{0,1\}\) are two ensembles of random variables indexed by \(\lambda \in \mathbb {N}\), we say that \(\mathcal {X}^{(0)}\) and \(\mathcal {X}^{(1)}\) are computationally indistinguishable if for any PPT distinguisher \(\mathcal {D}\), there exists a negligible function \({\mathsf {negl}}(\lambda )\), such that

We write \(\mathcal {X}^{(0)} {\mathop {\approx }\limits ^{\mathsf {c}}}\mathcal {X}^{(1)}\) to denote that the advantage \(\varDelta \) is negligible.
The statistical distance between \(\mathcal {X}^{(0)}\) and \(\mathcal {X}^{(1)}\) over a countable set S is defined as  . We say that \(\mathcal {X}^{(0)}\) and \(\mathcal {X}^{(1)}\) are statistically/perfectly indistinguishable (denoted by \(\mathcal {X}^{(0)} {\mathop {\approx }\limits ^{\mathsf {s}}}\mathcal {X}^{(1)}\)/\(\mathcal {X}^{(0)} {\mathop {\approx }\limits ^{\mathsf {p}}}\mathcal {X}^{(1)}\)) if \(\varDelta _{\mathsf {s}} (\mathcal {X}^{(0)},\mathcal {X}^{(1)}) \le {\mathsf {negl}}(\lambda )\) and \(\varDelta _{\mathsf {s}} (\mathcal {X}^{(0)},\mathcal {X}^{(1)}) =0\), respectively. We also say that \(\mathcal {X}^{(0)}\) is \(\epsilon \)-close to \(\mathcal {X}^{(1)}\) if \(\varDelta _{\mathsf {s}} (\mathcal {X}^{(0)},\mathcal {X}^{(1)}) = \epsilon \).
. We say that \(\mathcal {X}^{(0)}\) and \(\mathcal {X}^{(1)}\) are statistically/perfectly indistinguishable (denoted by \(\mathcal {X}^{(0)} {\mathop {\approx }\limits ^{\mathsf {s}}}\mathcal {X}^{(1)}\)/\(\mathcal {X}^{(0)} {\mathop {\approx }\limits ^{\mathsf {p}}}\mathcal {X}^{(1)}\)) if \(\varDelta _{\mathsf {s}} (\mathcal {X}^{(0)},\mathcal {X}^{(1)}) \le {\mathsf {negl}}(\lambda )\) and \(\varDelta _{\mathsf {s}} (\mathcal {X}^{(0)},\mathcal {X}^{(1)}) =0\), respectively. We also say that \(\mathcal {X}^{(0)}\) is \(\epsilon \)-close to \(\mathcal {X}^{(1)}\) if \(\varDelta _{\mathsf {s}} (\mathcal {X}^{(0)},\mathcal {X}^{(1)}) = \epsilon \).
Definition 2.1
(Circuit similarity). Let \(\mathcal {C}\) be a circuit class whose input space is \(\{0,1\}^{\ell }\). For two circuits \(C,C' \in \mathcal {C}\) and a non-decreasing function \(\epsilon : \mathbb {N}\rightarrow \mathbb {N}\), we say that C is \(\epsilon \)-close to \(C'\) if it holds that
Similarly, we say that C is \(\epsilon \)-far to \(C'\) if it holds that
3 Definitions of Watermarking for Cryptographic Primitives
In this section, we introduce the definitions of watermarking for cryptographic primitives. Although our definitions basically follow those of Goyal et al. [22], there are several differences.
We focus on cryptographic primitives that have a master parameter generation algorithm \(\mathsf {PGen}\) and a master secret-key based algorithm \(\mathsf {MSKAlg}\) in this study. For example, in IBE/ABE/IPE, \(\mathsf {PGen}\) is a setup algorithm \(\mathsf {Setup}\) and \(\mathsf {MSKAlg}\) is a key generation algorithm for identity/attribute/policy \(\mathsf {KeyGen}\). In TBE/KEM/signature, \(\mathsf {PGen}\) is a key generation algorithm \(\mathsf {Gen}\) and \(\mathsf {MSKAlg}\) is a decryption/signing algorithm \(\mathsf {Dec}\)/\(\mathsf {Sign}\). Hereafter, we do not explicitly treat KEM, but it is easy to adapt all definitions to the KEM setting. We formalize the notion of master secret-key based cryptographic schemes as follows.
Definition 3.1
(Master secret-key based cryptographic scheme). A master secret-key based cryptographic scheme \(\varSigma \) with spaces \((\mathcal {T},\mathcal {Q},\mathcal {P},\mathcal {R}_{\mathsf {mka}})\) has at least two algorithms \(\mathsf {PGen}\) and \(\mathsf {MSKAlg}\).
-
Master parameter generation: \(\mathsf {PGen}(1^\lambda )\) takes as input the security parameter and outputs a master public parameter \(\mathsf {PP}\in \mathcal {P}\mathcal {P}\) and a master secret key \(\mathsf {MSK}\in \mathcal {M}\mathcal {S}\mathcal {K}\). We often omit spaces \(\mathcal {P}\mathcal {P}\) and \(\mathcal {M}\mathcal {S}\mathcal {K}\) from \(\varSigma \).
-
Master secret-key based algorithm: \(\mathsf {MSKAlg}(\mathsf {MSK},X)\) takes \(\mathsf {MSK}\) and an input \(X \in \mathcal {Q}\) and outputs \(Y \in \mathcal {P}\). The randomness space of \(\mathsf {MSKAlg}\) is \(\mathcal {R}_{\mathsf {mka}}\).
We assume that \(\mathsf {MSK}\) includes \(\mathsf {PP}\). \(\varSigma = (\mathsf {PGen},\mathsf {MSKAlg},\ldots )\) has additional algorithm other than \(\mathsf {PGen}\) and \(\mathsf {MSKAlg}\). The space \(\mathcal {T}\) is used in the security game defined later (Definition 4.2).Footnote 14
Remark 3.1
In Definition 3.1, an output by \(\mathsf {MSKAlg}\) is typically a secret key for an identity/policy X, signature for a message X. In the TBE case, X consists of a tag and ciphertext, and Y is a plaintext. We can consider encryption, decryption, and verification algorithms as additional algorithms. Definition 3.1 captures most popular cryptographic schemes such as PKE, TBE, IBE, ABE, IPE, PE, FE, signature, constrained signature.
Definition 3.2
(Validity check algorithm for master secret-key based cryptographic scheme). A master secret-key based cryptographic scheme \(\varSigma \) with spaces \((\mathcal {T},\mathcal {Q},\mathcal {P},\mathcal {R}_{\mathsf {mka}})\) can have an optional algorithm \(\mathsf {Valid}\text {-}\mathsf {Out}\) that takes as inputs \(\mathsf {PP}\), \(X\in \mathcal {Q}\), and \(Y \in \mathcal {P}\) and outputs \(\top /\bot \). For all \((\mathsf {PP},\mathsf {MSK})\leftarrow \mathsf {PGen}(1^\lambda )\) and all \(X \in \mathcal {Q}\), \(\mathsf {Valid}\text {-}\mathsf {Out}(\mathsf {PP},X,Y)\) outputs \(\top \) if and only if \(Y \leftarrow \mathsf {MSKAlg}(\mathsf {MSK},X)\).
Remark 3.2
Although we do not explicitly consider validity check algorithms in signature and advanced encryption schemes, we can implement validity check algorithms in most schemes (and all schemes in this paper). See examples in Sects. 4.3 and 4.5. Note that Y is not necessarily unique since \(\mathsf {MSKAlg}\) might be a randomized algorithm.
Definition 3.3
(Watermarkable Public-Key Scheme). A watermarking scheme with mark space \(\mathcal {M}_{\mathsf{w}}\) for master secret-key based cryptographic scheme \(\varSigma \) with spaces \((\mathcal {T},\mathcal {Q},\mathcal {P},\mathcal {R}_{\mathsf {mka}})\) is a tuple of algorithms \((\mathsf {WM}\mathsf {Setup},\mathsf {Mark},\mathsf {Extract})\) with the following properties:
-
Setup: \(\mathsf {WM}\mathsf {Setup}(1^\lambda )\) takes as input the security parameter and outputs a watermarking public parameter \(\mathsf {wpp}\), a marking key \(\mathsf {wmk}\), and an extraction key \(\mathsf {wxk}\).
-
Mark: \(\mathsf {Mark}(\mathsf {wpp},\mathsf {wmk},\mathsf {MSK},\omega )\) takes as input \(\mathsf {wpp}\), \(\mathsf {wmk}\), the master secret key \(\mathsf {MSK}\in \mathcal {M}\mathcal {S}\mathcal {K}\) of \(\varSigma \), and a mark \(\omega \in \mathcal {M}_{\mathsf{w}}\) and outputs a deterministic circuit \(\widetilde{C}:\mathcal {Q}\times \mathcal {R}_{\mathsf {mka}}\rightarrow \mathcal {P}\). Note that \(\widetilde{C}\) explicitly takes the randomness of \(\mathsf {MSKAlg}\).
-
Extract: \(\mathsf {Extract}(\mathsf {wpp},\mathsf {wxk},\mathsf {PP},C')\) takes as input \(\mathsf {wpp}\), \(\mathsf {wxk}\), the public parameter \(\mathsf {PP}\in \mathcal {P}\mathcal {P}\) of \(\varSigma \), and a circuit \(C': \mathcal {Q}\times \mathcal {R}_{\mathsf {mka}}\rightarrow \mathcal {P}\) and outputs a mark \(\omega ' \in \mathcal {M}_{\mathsf{w}}\) or a special symbol \(\mathsf {unmarked}\).
Remark 3.3
We can separately treat watermarking schemes and cryptographic primitives in our definition while in the definition of Goyal et al. [22], key generation algorithms of cryptographic primitives need public parameters of watermarking. The separated definition is preferable and the same definition as that of Cohen et al. [19].
Hereafter, we set  since we consider only two cases. One is the public marking and extraction case (\(\mathsf {wmk}= \mathsf {wxk}=\bot \)) and the other is the secret marking and extraction case (\(\mathsf {wsk}= \mathsf {wmk}= \mathsf {wxk}\)) in this paper.
since we consider only two cases. One is the public marking and extraction case (\(\mathsf {wmk}= \mathsf {wxk}=\bot \)) and the other is the secret marking and extraction case (\(\mathsf {wsk}= \mathsf {wmk}= \mathsf {wxk}\)) in this paper.
Hereafter, we focus on advanced encryption (IBE, IPE, ABE, PE) rather than TBE and signature for readability. Due to space limitations, we omit the definitions for TBE and signature.
Definition 3.4
(Correctness (Advanced encryption)). Let \(\mathsf {WM}_\varSigma = (\mathsf {WM}\mathsf {Setup},\mathsf {Mark},\mathsf {Extract})\) be a watermarking scheme for advanced encryption scheme \(\varSigma =(\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})\) with spaces \((\mathcal {T},\mathcal {Q},\mathcal {P},\mathcal {R}_{\mathsf {mka}})\). In this case, \(\mathcal {T}=\mathcal {ATT}\), \(\mathcal {Q}=\mathcal {POL}\), \(\mathcal {P}=\mathcal {SK}\), where \(\mathcal {ATT}\) and \(\mathcal {POL}\) is an attribute and policy space, respectively. We say that \(\mathsf {WM}_\varSigma \) is correct if it satisfies the following.
-
Extraction correctness: For all \((\mathsf {wpp},\mathsf {wsk}) \leftarrow \mathsf {WM}\mathsf {Setup}(1^\lambda )\), all marks \(\omega \in \mathcal {M}_{\mathsf{w}}\),
$$ \Pr \left[ \mathsf {Extract}(\mathsf {wpp},\mathsf {wsk},\mathsf {PP},\widetilde{C}) \ne \omega \ \left| \begin{array}{rl} (\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda )\\ \widetilde{C}\leftarrow \mathsf {Mark}(\mathsf {wpp},\mathsf {wsk},\mathsf {MSK},\omega ) \end{array}\right. \right] \le {\mathsf {negl}}(\lambda ). $$ -
Meaningfulness: There are two variants of meaningfulness.
Strong meaningfulness. For all fixed circuits \(C:\mathcal {POL}\times \mathcal {R}_{\mathsf {mka}}\rightarrow \mathcal {SK}\),
$$ \Pr \left[ \begin{array}{rl} &{}\mathsf {Extract}(\mathsf {wpp},\mathsf {wsk},\mathsf {PP},C) \\ = &{}\mathsf {unmarked}\end{array} \ \left| \begin{array}{rl} &{}(\mathsf {wpp},\mathsf {wsk}) \leftarrow \mathsf {WM}\mathsf {Setup}(1^\lambda ) \\ &{}(\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda ) \ \end{array}\right. \right] > 1- {\mathsf {negl}}(\lambda ). $$Weak meaningfulness. For all \((\mathsf {wpp},\mathsf {wsk}) \leftarrow \mathsf {WM}\mathsf {Setup}(1^\lambda )\),
$$ \Pr \left[ \begin{array}{rl} &{}\mathsf {Extract}(\mathsf {wpp},\mathsf {wsk},\mathsf {PP},\mathsf {KeyGen}(\mathsf {MSK},\cdot )) \\ =&{} \mathsf {unmarked}\end{array} \ \left| (\mathsf {PP},\mathsf {MSK})\leftarrow \mathsf {Setup}(1^\lambda )\right. \right] > 1- {\mathsf {negl}}(\lambda ). $$ -
Functionality-preserving: For all \((\mathsf {wpp},\mathsf {wsk})\leftarrow \mathsf {WM}\mathsf {Setup}(1^\lambda )\), for all \((\mathsf {PP},\mathsf {MSK})\leftarrow \mathsf {Setup}(1^\lambda )\), all marks \(\omega \in \mathcal {M}_{\mathsf{w}}\), there exists \(\mathcal {P}\mathcal {S}\subset \mathcal {ATT}\) such that
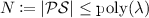 , for all \(\rho _\mathsf {mka}\in \mathcal {R}_{\mathsf {mka}}\), all attributes \(x \in \mathcal {ATT}\setminus \mathcal {P}\mathcal {S}\) and all policy \(\mathsf{P} \in \mathcal {POL}\) such that \(\mathsf{P}(x)=\top \), we have that $$ \Pr [\widetilde{C}(\mathsf{P},\rho _\mathsf {mka}) {\mathop {\approx }\limits ^{\mathsf {p}}}\mathsf {KeyGen}(\mathsf {MSK},\mathsf{P}) \mid \widetilde{C}\leftarrow \mathsf {Mark}(\mathsf {wpp},\mathsf {wsk},\mathsf {MSK},\omega )] > 1- {\mathsf {negl}}(\lambda ). $$
, for all \(\rho _\mathsf {mka}\in \mathcal {R}_{\mathsf {mka}}\), all attributes \(x \in \mathcal {ATT}\setminus \mathcal {P}\mathcal {S}\) and all policy \(\mathsf{P} \in \mathcal {POL}\) such that \(\mathsf{P}(x)=\top \), we have that $$ \Pr [\widetilde{C}(\mathsf{P},\rho _\mathsf {mka}) {\mathop {\approx }\limits ^{\mathsf {p}}}\mathsf {KeyGen}(\mathsf {MSK},\mathsf{P}) \mid \widetilde{C}\leftarrow \mathsf {Mark}(\mathsf {wpp},\mathsf {wsk},\mathsf {MSK},\omega )] > 1- {\mathsf {negl}}(\lambda ). $$Here, \(\mathcal {P}\mathcal {S}\) stands for a “punctured set” since \(\widetilde{C}\) does not work for policy \(\mathsf{P}\) such that \(x\in \mathcal {P}\mathcal {S}\) and \(\mathsf{P}(x)=\bot \).
Condition \(\mathsf{P}(x)=\bot \) means attribute x is not qualified to policy \(\mathsf{P}\).
In the IBE case, \(\mathcal {T}= \mathcal {Q}= \mathcal {ID}\) (identity space), \(\mathsf{P} = \mathsf {id}_i\), \(x = \mathsf {id}\), and \(\mathsf{P}(x)=\bot \) means \(\mathsf {id}_i \ne \mathsf {id}\).
Remark 3.4
Although our definition has a few differences from the standard functionality preserving in the cryptographic watermarking context [19, 32] on the surface, ours is basically the same as the standard one. We select the definition above to emphasize that there exists a punctured set \(\mathcal {P}\mathcal {S}\), and the set is explicitly used in the security definition.
In addition, this functionality-preserving is stronger than that by Goyal et al. [22] since the output distribution of marked circuits is perfectly the same as that of the original circuit on almost all inputs.
Definition 3.5
(Selective-Mark \(\epsilon \)-Unremovability for Advanced Encryption). For every PPT \(\mathcal {A}\), we have
where \(\epsilon \) is a parameter of the scheme called the approximation factor and \(\mathsf {Exp}_{\mathcal {A},\mathsf {WM}_\varSigma }^{ \mathsf {urmv} \text{- } \mathsf {enc}}(\lambda ,\epsilon )\) is the game defined as follows.
-
1.
The adversary \(\mathcal {A}\) declares a target mark \(\omega ^* \in \mathcal {M}_{\mathsf{w}}\).
-
2.
The challenger generates \((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda )\), \((\mathsf {wpp},\mathsf {wsk})\leftarrow \mathsf {WM}\mathsf {Setup}(1^\lambda )\), and \(\widetilde{C}\leftarrow \mathsf {Mark}(\mathsf {wpp},\mathsf {wsk},\mathsf {MSK},\omega ^*)\), and gives \((\mathsf {PP},\mathsf {wpp},\widetilde{C})\) to \(\mathcal {A}\). At this point, a set \(\mathcal {P}\mathcal {S}\subset \mathcal {T}\) such that \(|\mathcal {P}\mathcal {S}|={\mathrm {poly}}(\lambda )\) is uniquely determined by \((\mathsf {wpp},\mathsf {wsk},\mathsf {PP},\omega ^*)\).
-
3.
\(\mathcal {A}\) has oracle access to the key generation oracle \(\mathcal {K}\mathcal {O}\). If \(\mathcal {K}\mathcal {O}\) is queried with a policy \(\mathsf{P} \in \mathcal {POL}\) such that \(\mathsf{P}(t^{*}_i)=\bot \) for all \(t^{*}_i \in \mathcal {P}\mathcal {S}\), then \(\mathcal {K}\mathcal {O}\) answers with \(\mathsf {KeyGen}(\mathsf {MSK},\mathsf{P})\). Otherwise, it answers \(\bot \). Condition \(\mathsf{P}(x)=\bot \) means attribute x is not qualified to policy \(\mathsf{P}\).
-
4.
\(\mathcal {A}\) has oracle access to the marking oracle \(\mathcal {M}\mathcal {O}\). If \(\mathcal {M}\mathcal {O}\) is queried with a master secret key \(\mathsf {MSK}' \in \mathcal {M}\mathcal {S}\mathcal {K}\) and a mark \(\omega ' \in \mathcal {M}_{\mathsf{w}}\), then does the following. If the corresponding master public parameter \(\mathsf {PP}'\) is equal to \(\mathsf {PP}\), then outputs \(\bot \). Otherwise, answers with \(\mathsf {Mark}(\mathsf {wpp},\mathsf {wsk},\mathsf {MSK}',\omega ')\).
-
5.
\(\mathcal {A}\) has oracle access to the extraction oracle \(\mathcal {X}\mathcal {O}\). If \(\mathcal {X}\mathcal {O}\) is queried with a \(\mathsf {PP}'\) and circuit \(C'\), then \(\mathcal {X}\mathcal {O}\) answers with \(\mathsf {Extract}(\mathsf {wpp},\mathsf {wsk},\mathsf {PP}',C')\).
-
6.
Finally, \(\mathcal {A}\) outputs a circuit \(C^{*}\). If \(\mathcal {A}\) is admissible (defined below) and \(\mathsf {Extract}(\mathsf {wpp},\mathsf {wsk},\mathsf {PP}, C^{*}) \ne \omega ^*\) then the experiment outputs 1, otherwise 0.
We say that \(\mathcal {A}\) is \(\epsilon \)-admissible if \(C^*\) output by \(\mathcal {A}\) in the experiment above satisfies
See Definition 3.2 for \(\mathsf {Valid}\text {-}\mathsf {Out}\).
The admissibility requires the adversary to output \(C^{*}\) that agrees on an \(\epsilon \) fraction of inputs with C. This formalizes that \(C^{*}\) should be similar to the original circuit C.
Remark 3.5
Our definition is the same as that of Goyal et al. [22] except for that
-
1.
\(\mathcal {A}\) must declare the target mark \(\omega \) at the beginning of the game.
-
2.
\(\mathcal {A}\) does not receives answers for inputs in \(\mathcal {P}\mathcal {S}\) from the key generation oracle.
-
3.
we do not consider collusion-resistance w.r.t. watermarking. That is, \(\mathcal {A}\) is given only one target circuit \(\widetilde{C}\).
-
4.
we consider the oracles \(\mathcal {K}\mathcal {O}\) in the unremovability game while Goyal et al. do not.
-
5.
we consider watermarking for master secret-keys. Thus, the admissible condition for advanced encryption (i.e., beyond PKE or TBE) is in terms of \(\mathsf {Valid}\text {-}\mathsf {Out}\).
Unforgeability. We can consider another security notion for watermarking, called unforgeability [12, 19, 32], in the secret marking setting. Unforgeability says that adversaries cannot generate a marked circuit with sufficiently different functionality from that of given marked circuits without a marking key.
We do not formally define unforgeability in this work as Goyal et al. did not. However, we can achieve unforgeability by embedding not only a mark but also a signature for the embedded mark and master public key as Goyal et al. observed [22].Footnote 15
On Security Against Malicious Authority. Our watermarkable public-key primitives are trivially secure against authorities of watermarking schemes if the underlying public-key primitives are secure since parameter generation algorithms \(\mathsf {PGen}\) are independent of watermarking setup algorithms \(\mathsf {WM}\mathsf {Setup}\). Thus, we omit the definition of security against malicious authority.
4 All-But-One Reductions
In this section, we formalize a class of security reductions, called canonical all-but-one (ABO) reductions. Canonical ABO reductions are often used to prove the hardness of breaking many cryptographic primitives. A typical example is the security reduction of Boneh-Boyen IBE based on the decisional bilinear Diffie-Hellman assumption [9].
4.1 Assumptions and Security Games
We need to define cryptographic assumptions and security games before we formalize canonical ABO reductions. The types of reductions depend on whether security games and underlying cryptographic assumptions are computational or decisional. Therefore, we consider two types of assumptions and games. However, we focus on the decisional case in the main body for readability. See the full version for the computational case.
Definition 4.1
(Decisional assumption). A decisional assumption \(\mathsf {DA}\) for problem \(\varPi \) is formalized by a game between the challenger \(\mathcal {E}\) and the adversary \(\mathcal {A}\). The problem \(\varPi \) consists of an efficient problem sampling algorithm \(\mathsf {PSample}_{b}\) for \(b\in \{0,1\}\). The game \(\mathsf {Expt}_{\varPi ,\mathcal {E}\leftrightarrow \mathcal {A}}^{\mathsf {DA}}(\lambda ,b)\) is formalized as follows.
-
On input security parameter \(\lambda \), \(\mathcal {E}\) samples a problem instance \(\pi _b \leftarrow \mathsf {PSample}_b(1^\lambda )\).
-
\(\mathcal {E}\) sends \(\pi _b\) to \(\mathcal {A}\) and may interact with \(\mathcal {A}(1^\lambda ,\pi _b)\).
-
At some point, \(\mathcal {A}\) outputs a guess \(\mathsf {coin}^{*}\) and the game outputs \(\mathsf {coin}^{*}\).
We say a decisional assumption holds (or problem \(\varPi \) is hard) if it holds

This definition captures the well-known DDH, DBDH, k-Lin, matrix-DDH, quadratic residuosity, LWE, decisional q-type assumptions (and more). Note that the assumption above also captures interactive oracle assumptions since \(\mathcal {A}\) may interact with the challenger that plays the role of oracles.
Definition 4.2
(Selective Security Game (Decisional Case)). We define selective security games (decisional case) between a challenger \(\mathcal {C}\) and an adversary \(\mathcal {A}\) for a master secret-key based scheme \(\varSigma \) with spaces \((\mathcal {T},\mathcal {Q},\mathcal {P},\mathcal {R}_{\mathsf {mka}})\) associated with challenge space \(\mathcal {H}\), challenge answer space \(\mathcal {I}\), and admissible condition \(\mathsf {Adml}\). (See Table 4 for concrete examples.) The admissible condition \(\mathsf {Adml}\) outputs \(\top \) or \(\bot \) depending on whether a query is allowed or not.
We define the experiment \(\mathsf {Exp}_{\mathcal {A},\varSigma }^{ \mathsf {d} \text{- } \mathsf {goal} \text{- } \mathsf {atk}}(\lambda ,\mathsf {coin})\) between an adversary \(\mathcal {A}\) and a challenger as follows.
-
1.
\(\mathcal {A}\) submits a target \(t^{*}\in \mathcal {T}\) to the challenger.
-
2.
The challenger runs \((\mathsf {PP},\mathsf {MSK})\leftarrow \mathsf {PGen}(1^\lambda )\), and gives \(\mathsf {PP}\) to \(\mathcal {A}\).
-
3.
\(\mathcal {A}\) sends a query \(\mathsf {query}\in \mathcal {Q}\) to the challenger. If \(\mathsf {Adml}(t^{*},\mathsf {query})=\top \), the challenger sends an answer \(\mathsf {answer}\leftarrow \mathsf {MSKAlg}(\mathsf {MSK},\mathsf {query})\) to \(\mathcal {A}\). On the other hand, if \(\mathsf {Adml}(t^{*},\mathsf {query})=\bot \), the challenger outputs \(\bot \). (\(\mathcal {A}\) can send polynomially many queries.)
-
4.
At some point, \(\mathcal {A}\) sends a challenge \(\mathsf {challenge}\in \mathcal {H}\) to the challenger. The challenger generates a challenge answer \(\mathsf {c}\text {-}\mathsf {ans}^*\in \mathcal {I}\) by using \((t^{*},\mathsf {PP},\mathsf {challenge},\mathsf {coin})\) (denoted by \(\mathcal {C}_{\mathsf{a}} (t^{*},\mathsf {PP},\mathsf {challenge},\mathsf {coin})\)) and sends \(\mathsf {c}\text {-}\mathsf {ans}^*\) to \(\mathcal {A}\).
-
5.
Again, \(\mathcal {A}\) is allowed to query (polynomially many) \(\mathsf {query}\in \mathcal {Q}\) such that \(\mathsf {Adml}(t^{*},\mathsf {query})=\top \).
-
6.
\(\mathcal {A}\) outputs a guess \(\mathsf {coin}^{*}\) for \(\mathsf {coin}\). The experiment outputs \(\mathsf {coin}^{*}\).
We say that \(\varSigma \) is secure if for all \(\mathcal {A}\), it holds that

We say an adversary is successful if the advantage is non-negligible. We can consider the multi-challenge case, where the targets are \(\mathbf {t}^{*}\in \mathcal {T}^N\) instead of the single \(t^{*}\).
A concrete example of \(\mathsf {Adml}(t^{*},\mathsf {query})\) is \(\mathsf {Adml}(t^{*},\mathsf {query})= \top \) if and only if \(t^{*}\ne t\) where \(\mathsf {query}=t\) in the signature/TBE/IBE cases (t is a message/tag/identity).
Although we can consider a stronger variant, called adaptive security games, we consider only selective security games since ABO reductions are basically applicable in the selective setting.
4.2 Abstraction of All-But-One Reductions for Decisional Case
Now, we are ready to define ABO reductions for the decisional case. We put red underlines on the parts related to “canonical” parts.
First, we present a simplified definition that does not capture the TBE/KEM case for readability.
Definition 4.3
(Canonical All-But-One Reduction for Decisional Case (Simplified)). Let \(\varSigma \) be a master secret-key based scheme with \((\mathcal {T},\mathcal {Q},\mathcal {P},\mathcal {R}_{\mathsf {mka}})\) associated with challenge space \(\mathcal {H}\), challenge answer space \(\mathcal {I}\), and admissible condition \(\mathsf {Adml}\). (See Table 4 for concrete examples.) A security reduction algorithm \(\mathsf {R}\) from \(\varSigma \) to a hard problem \(\varPi \) is a canonical all-but-one reduction (or \(\varSigma \) has a canonical all-but-one reduction to \(\varPi \)) if it satisfies the following properties.
-
Oracle access: \(\mathcal {A}\) has oracle access to \(\mathcal { O}_{\mathsf {MSK}}: \mathcal {Q}\rightarrow \mathcal {P}\) in the security game \(\mathsf {Exp}_{\mathcal {A},\varSigma }^{ \mathsf {d} \text{- } \mathsf {goal} \text{- } \mathsf {atk}}\). This oracle receives a query \(\mathsf {query}\in \mathcal {Q}\) and does the following. If \(\mathsf {Adml}(t^{*},\mathsf {query})=\top \), where \(t^{*}\) is defined below, it sends an answer \(\mathsf {answer}\leftarrow \mathsf {MSKAlg}(\mathsf {MSK},\mathsf {query})\) to \(\mathcal {A}\). On the other hand, if \(\mathsf {Adml}(t^{*},\mathsf {query})=\bot \), it outputs \(\bot \).
-
Selective reduction: \(\mathsf {R}\) simulates the security game \(\mathsf {Exp}_{\mathcal {A},\varSigma }^{ \mathsf {d} \text{- } \mathsf {goal} \text{- } \mathsf {atk}}\) of \(\varSigma \) between the challenger \(\mathcal {C}\) and the adversary \(\mathcal {A}\) to win the game \(\mathsf {Expt}_{\varPi ,\mathcal {E}\leftrightarrow \mathsf {R}}^{\mathsf {DA}}\). That is, \(\mathsf {R}\) plays the role of the challenger \(\mathcal {C}\) in \(\mathsf {Exp}_{\mathcal {A},\varSigma }^{ \mathsf {d} \text{- } \mathsf {goal} \text{- } \mathsf {atk}}\) and that of the adversary in \(\mathsf {Expt}_{\varPi ,\mathcal {E}\leftrightarrow \mathsf {R}}^{\mathsf {DA}}\).
-
1.
\(\mathcal {A}\) declares an arbitrary string \(t^{*}\in \mathcal {T}\) at the very begining of the game and send \(t^{*}\) to \(\mathsf {R}\). (We can allow \(\mathsf {R}\) to determine \(t^{*}\) in some security games.)
-
2.
\(\mathsf {R}\) is given a problem instance \(\pi \) of the hard problem \(\varPi \).
-
3.
\(\mathsf {R}\) simulates public parameters \(\mathsf {PP}\) of \(\varSigma \) by using \(\pi \) and \(t^{*}\) and sends \(\mathsf {PP}\) to \(\mathcal {A}\).
-
4.
\(\mathsf {R}\) simulates an oracle \(\mathcal { O}_{\mathsf {MSK}}\) of the security game of \(\varSigma \) when \(\mathcal {A}\) sends oracle queries. That is, when \(\mathcal {A}\) sends a query \(\mathsf {query}\in \mathcal {Q}\), \(\mathsf {R}\) simulates the value \(\mathcal { O}_{\mathsf {MSK}}(\mathsf {query})\) and returns a simulated value \(\mathsf {answer}\in \mathcal {P}\) to \(\mathcal {A}\). If \(\mathsf {Adml}(t^{*},\mathsf {query})=\bot \), then \(\mathsf {R}\) outputs \(\bot \).
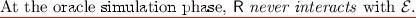
-
5.
At some point, \(\mathcal {A}\) sends a challenge query \(\mathsf {challenge}\in \mathcal {H}\) to \(\mathsf {R}\).
-
6.
\(\mathsf {R}\) chooses \(\mathsf {coin}\leftarrow \{0,1\}\) and simulates a challenge answer \(\mathsf {c}\text {-}\mathsf {ans}^*\in \mathcal {I}\) of \(\mathcal {C}_{\mathsf{a}} (\mathsf {PP},t^{*},\mathsf {challenge},b)\) by using \((\pi ,\mathsf {PP},t^{*},\mathsf {challenge},\mathsf {coin})\). It sends \(\mathsf {c}\text {-}\mathsf {ans}^*\) to \(\mathcal {A}\). \(\mathsf {R}\) is allowed to interact with \(\mathcal {E}\) at this phase.
-
7.
We can allow \(\mathcal {A}\) to send queries to \(\mathcal { O}_{\mathsf {MSK}}\) again. At some point, \(\mathcal {A}\) outputs \(\mathsf {coin}^{*}\).
-
8.
Finally, \(\mathsf {R}\) outputs a bit
 if \(\mathsf {coin}=\mathsf {coin}^{*}\). Otherwise (\(\mathsf {coin}\ne \mathsf {coin}^{*}\)), outputs
if \(\mathsf {coin}=\mathsf {coin}^{*}\). Otherwise (\(\mathsf {coin}\ne \mathsf {coin}^{*}\)), outputs  .
.
\(\mathsf {R}\) consists of three algorithms \((\mathsf {PSim},\mathsf {OSim},\mathsf {CSim})\) introduced below.
-
1.
-
All-but-one oracle simulation: \(\mathsf {R}\) can perfectly simulate the public parameter of \(\varSigma \) and the oracle \(\mathcal { O}_{\mathsf {MSK}}\). That is, there exist parameter and oracle simulation algorithms \(\mathsf {PSim}\) and \(\mathsf {OSim}\) such that for all \((\mathsf {PP},\mathsf {MSK})\leftarrow \mathsf {PGen}(1^\lambda )\), \(b\in \{0,1\}^{}\), \(\pi \leftarrow \mathsf {PSample}_{b}(1^\lambda )\), \(t^{*}\in \mathcal {T}\), and \(\mathsf {query}\in \mathcal {Q}\) where \(\mathsf {Adml}(t^{*},\mathsf {query})=\top \), it holds that
$$\begin{aligned} \mathsf {PSim}(\pi ,t^{*};\rho )&\,{\mathop {\approx }\limits ^{\mathsf {p}}}\, \mathsf {PP},\\ \mathsf {OSim}(\pi ,\rho ,t^{*},\mathsf {query})&\,{\mathop {\approx }\limits ^{\mathsf {p}}}\,\mathcal { O}_\mathsf {MSK}(\mathsf {query}), \end{aligned}$$where \(\rho \) is the randomness of \(\mathsf {PSim}\). Note that a query \(\mathsf {query}\) such that \(\mathsf {Adml}(t^{*},\mathsf {query})=\bot \) is not allowed in the selective security game of \(\varSigma \).
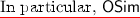
-
-
Challenge simulation Let \(\rho \) be the randomness used by \(\mathsf {PSim}\). \(\mathsf {R}\) does all the steps from (1) to (5) in the selective reduction above and can simulate the challenge answer for the challenge query from \(\mathcal {A}\). That is, there exists a challenge simulation algorithm \(\mathsf {CSim}\) such that in the selective game above, if \(\pi _0 \leftarrow \mathsf {PSample}_0(1^\lambda )\), then \(\mathsf {R}\) perfectly simulates \(\mathsf {Exp}_{\mathcal {A},\varSigma }^{ \mathsf {d} \text{- } \mathsf {goal} \text{- } \mathsf {atk}}(\lambda ,\mathsf {coin})\) and it holds that
$$\begin{aligned} \mathsf {CSim}(\pi _0,\rho ,t^{*},\mathsf {challenge},\mathsf {coin})&\,{\mathop {\approx }\limits ^{\mathsf {p}}}\, \mathcal {C}_{\mathsf{a}}(\mathsf {PP},t^{*},\mathsf {challenge},\mathsf {coin}). \end{aligned}$$In addition, if \(\pi _1 \,{\leftarrow }\, \mathsf {PSample}_1(1^\lambda )\), then the output of \(\mathsf {CSim}(\pi _1,\rho ,t^{*},\mathsf {challenge}, \mathsf {coin})\) is a valid challenge answer, but independent of \(\mathsf {coin}\) and \(\Pr [\mathsf {coin}= \mathsf {coin}^{*}] = \frac{1}{2}\). This property immediately implies
$$ \mathsf {Adv}_{\varPi ,\mathcal {E}\leftrightarrow \mathsf {R}}^{\mathsf {DA}}(\lambda ) \ge \frac{1}{2}\mathsf {Adv}_{\mathcal {A},\varSigma }^{\mathsf {d} \text{- } \mathsf {goal} \text{- } \mathsf {atk}}(\lambda ). $$Due to space limitations, we omit the proof.
-
Answer checkability: There exists an efficient validity check algorithm \(\mathsf {Valid}\) for \(\mathcal {Q}\) such that for all \((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {PGen}(1^\lambda )\), \(\mathsf {query}\leftarrow \mathcal {Q}\), \(\mathsf {answer}\leftarrow \mathcal { O}_\mathsf {MSK}(\mathsf {query})\),
$$ \Pr [\mathsf {Valid}(\mathsf {PP},\mathsf {query},\mathsf {answer}) =\top ] = 1 -{\mathsf {negl}}(\lambda ). $$On the other hand, for all \(b\in \{0,1\}^{}\), \(\pi \leftarrow \mathsf {PSample}_{b}(1^\lambda )\), \(t^{*}\in \mathcal {T}\), \(\mathsf {PP}\leftarrow \mathsf {PSim}(\pi ,t^{*};\rho )\), \(\mathsf {query}\) such that \(\mathsf {Adml}(t^{*},\mathsf {query})=\bot \),
$$ \Pr [\mathsf {Valid}(\mathsf {PP},\mathsf {query},\mathsf {OSim}(\pi ,\rho ,t^{*},\mathsf {query})) =\top ] \le {\mathsf {negl}}(\lambda ). $$ -
Attack substitution: \(\mathsf {R}\) can solve a problem \(\pi \) if we have a valid answer \(\mathsf {answer}^* \in \mathcal {P}\) for \(\mathsf {query}^* \in \mathcal {Q}\) such that \(\mathsf {Adml}(t^{*},\mathsf {query}^*)=\bot \) (i.e., inadmissible query) instead of a successful adversary \(\mathcal {A}\) in the selective reduction. That is, there exists an efficient algorithm \(\mathsf {Solve}\) such that for all \(b\in \{0,1\}^{}\), \(\pi \leftarrow \mathsf {PSample}_{b}(1^\lambda )\), \(t^{*}\in \mathcal {T}\), \(\mathsf {query}^* \in \mathcal {Q}\), \(\mathsf {answer}^* \in \mathcal {P}\) such that \(\mathsf {Valid}(\mathsf {PP},\mathsf {query}^*,\mathsf {answer}^*) = \top \) and \(\mathsf {Adml}(t^{*},\mathsf {query}^*)=\bot \), we have that \(\mathsf {Solve}(\pi ,\rho ,t^{*},\mathsf {query}^*,\mathsf {answer}^*)\) outputs \(\mathsf {sol}\) for \(\pi \) and
$$ \mathsf {Adv}_{\varPi ,\mathcal {E}\leftrightarrow \mathsf {R}}^{\mathsf {DA}}(\lambda ) > {\mathsf {negl}}(\lambda ), $$where \(\rho \) is the randomnesses to sample \(\mathsf {PP}\) in the selective reduction.
-
Problem instance simulation: We can perfectly simulate a problem instance and randomness used to generate \(\mathsf {PP}\) in \(\mathsf {PSim}\) if we have a master secret key of \(\varSigma \). That is, there exists an efficient algorithm \(\mathsf {MSKtoP}\) such that for all \((\mathsf {PP},\mathsf {MSK})\leftarrow \mathsf {PGen}(1^\lambda )\), \(\pi \leftarrow \mathsf {PSample}_0(1^\lambda )\), all \(\rho \leftarrow \mathcal {R}_{\mathsf {PSim}}\), and all \(t^{*}\in \mathcal {T}\),
$$ (\pi ^\prime ,\rho ',\mathsf {PP}) \,{\mathop {\approx }\limits ^{\mathsf {p}}}\, (\pi ,\rho ,\mathsf {PP}^\prime ), $$where \((\pi ^\prime ,\rho ') \leftarrow \mathsf {MSKtoP}(1^\lambda ,\mathsf {MSK},t^{*})\), \(\mathsf {PP}^\prime = \mathsf {PSim}(\pi ,t^{*};\rho )\), \(\rho '\) is a randomness to simulate \(\mathsf {PP}\) via \(\mathsf {PSim}\), and \(\mathcal {R}_{\mathsf {PSim}}\) is the randomness space of \(\mathsf {PSim}\). We can relax this condition to statistical indistinguishability for uniformly random \(t^{*}\) (instead of all \(t^{*}\in \mathcal {T}\)).
On Canonical Property. As we can see in concrete examples (not only) in Sects. 4.3 and 4.5 (but also in many works), well-known selectively secure schemes have canonical ABO reductions. If a scheme has a reduction that must interact with the challenger in an assumption to simulate \(\mathcal { O}_{\mathsf {MSK}}\), then the reduction is not canonical. Interestingly, even if a reduction is allowed to interact with the challenger, the reduction could be canonical as long as the reduction does not need the interaction for simulating \(\mathcal { O}_{\mathsf {MSK}}\). More specifically, a canonical reduction is allowed to interact with the challenger in the assumption to simulate a challenge answer. See the full version for such an example.
Due to space limitations, we omit the general definition of canonical ABO reductions that also captures the TBE case.
Table 4 shows concrete example of spaces and oracles for various cryptographic primitives.
On Validity Check Algorithm. The validity check algorithm in Definition 4.3 verifies that a value in \(\mathcal {P}\) is a correct value for input \(\mathsf {query}\in \mathcal {Q}\). Let \(\rho _\mathsf {mka}\leftarrow \mathcal {R}_{\mathsf {mka}}\) and \(\mathsf {answer}= C(\mathsf {query},\rho _\mathsf {mka})\). Then, \(\mathsf {Valid}\) is described as follows.

4.3 Concrete Examples
First, we list the references of well-known schemes that fall into the class of canonical ABO reductions [2, 3, 6, 9,10,11, 13, 15, 20, 21, 25, 31, 34, 40, 43]. Note that this is not the exhaustive list.
Next, we present concrete examples by picking up well-known selectively secure schemes. We often omit parameters if it is clear from the context.
Example 4.1
(Boneh-Boyen IBE). The Boneh-Boyen IBE scheme \(\mathsf {BB}\) consists of the following algorithms.
-
\(\mathsf {Setup}(1^\lambda ):\)
-
Generate
 .
. -
Choose \(x,y \leftarrow \mathbb {Z}_p\) and \(h\leftarrow \mathbb {Z}_p\) and set
 .
. -
Output
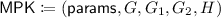 and
and 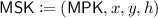 .
.
-
-
\(\mathsf {KeyGen}(\mathsf {MSK},\mathsf {id}):\)
-
For \(\mathsf {id}\in \mathbb {Z}_p\), choose \(r\leftarrow \mathbb {Z}_p\) and output
 .
.
-
-
\(\mathsf {Enc}(\mathsf {MPK}, m):\)
-
For \(M\in \mathbb {G}_T\), choose \(s\leftarrow \mathbb {Z}_p\) and output
 .
.
-
-
\(\mathsf {Dec}(\mathsf {SK}_\mathsf {id}, \mathsf {CT}):\)
-
Parse \(\mathsf {sk}_\mathsf {id}= (D_1,D_2)\) and \(\mathsf {CT}= (C_0,C_1,C_2)\), output \(C_0 \cdot e(C_2,D_2) \cdot e(C_1,D_1)^{-1}\).
-
The reduction algorithm \(\mathsf {R}\) of \(\mathsf {BB}\) IBE scheme consists of three algorithms \((\mathsf {PSim},\mathsf {OSim},\mathsf {CSim})\). Below, we let  ,
,  ,
,  ,
,  ,
,  ,
,  , be a DBDH instance, the target identity, a query to the key generation oracle, a sub-query, the randomness to sample \(\overline{\mathsf {query}}\in \overline{\mathcal {Q}}_{\mathsf {aux}}\), the challenge messages, respectively.
, be a DBDH instance, the target identity, a query to the key generation oracle, a sub-query, the randomness to sample \(\overline{\mathsf {query}}\in \overline{\mathcal {Q}}_{\mathsf {aux}}\), the challenge messages, respectively.
-
\(\mathsf {PSim}(\pi ,t^{*})\): This algorithm is given a DBDH instance \(\pi \) and a target identity \(t^{*}=\mathsf {id}^*\) and simulate \(\mathsf {MPK}\). It chooses \(\beta \leftarrow \mathbb {Z}_p\), sets
 ,
, 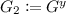 , and
, and  , and outputs
, and outputs  . The randomness \(\rho \) of this algorithm is
. The randomness \(\rho \) of this algorithm is 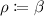
-
\(\mathsf {OSim}(\pi ,\rho ,t^{*},\mathsf {query})\): This algorithms simulate secret keys for identity \(\mathsf {query}= \mathsf {id}_i \in \mathbb {Z}_p\) such that \(\mathsf {id}_i \ne \mathsf {id}^* = t^{*}\). It parses \(\rho = \beta \), chooses \(r \leftarrow \mathbb {Z}_p\) and outputs \(\mathsf {SK}_{\mathsf {id}_i} = (D_1,D_2)\) where

The randomness \(\rho _{\mathsf{o}}\) of this algorithm is \(\rho _{{\mathsf{o}}} = r\).
-
\(\mathsf {CSim}(\pi ,\rho ,t^{*},\mathsf {challenge},\mathsf {coin})\): This algorithms simulate a challenge ciphertext for \(\mathsf {challenge}=(M_0,M_1)\) under identity \(t^{*}=\mathsf {id}^*\). It parses \(\rho = \beta \) and outputs
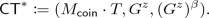
The auxiliary ABO reduction algorithms of \(\mathsf {BB}\) IBE scheme consists of three algorithms \((\mathsf {Valid},\mathsf {Solve},\mathsf {MSKtoP})\).
-
\(\mathsf {Valid}(\mathsf {MPK},\mathsf {query},\rho _{\mathsf{q}},\mathsf {answer})\): This algorithm parses \(\mathsf {MPK}= (G,G_1,G_2,H)\), \(\mathsf {query}= (\mathsf {id},\bot )\), \(\rho _{\mathsf{q}} =\bot \), and \(\mathsf {answer}= (D_1,D_2)\) (this is secret key \(\mathsf {SK}_\mathsf {id}\) for identity \(\mathsf {id}\)) and checks
$$\begin{aligned} e(G,D_1) = e(G_1,G_2) \cdot e(G_1^\mathsf {id}H, D_2). \end{aligned}$$(1)If it holds, then output \(\top \). Otherwise, outputs \(\bot \).
-
\(\mathsf {Solve}(\pi ,\rho ,t^{*},\mathsf {query}^*,\rho _{\mathsf{q}},\mathsf {answer}^*)\): First, this algorithm parses \(\mathsf {id}^* =t^{*}\), \(\mathsf {query}^* = (\mathsf {id}^*,\bot )\), \(\rho = \beta \), and \(\rho _{\mathsf{q}} = \bot \). It chooses \(M_0,M_1\) and \(\mathsf {coin}\leftarrow \{0,1\}\) and computes

(this is the same as the output of \(\mathsf {CSim}(\pi ,\rho ,t^{*},\mathsf {challenge},\mathsf {coin})\)). Then, it parses \(\mathsf {answer}^* = (G_2^{x}(G_1^{\mathsf {id}^*} H)^r,G^r)\) and decrypts \(\mathsf {CT}^*\) by using \((G_2^{x}(G_1^{\mathsf {id}^*} H)^r,G^r)\). If it obtains \(M_\mathsf {coin}\), then outputs 0, otherwise 1.
-
\(\mathsf {MSKtoP}(1^\lambda ,\mathsf {MSK},t^{*})\): First, this algorithms parses \(\mathsf {MSK}=(\mathsf {MPK}, x,y,h)\), chooses \(z\leftarrow \mathbb {Z}_p\), and computes
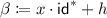 . Then, it outputs
. Then, it outputs  and
and 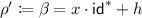 .
.
Theorem 4.1
Boneh-Boyen IBE scheme has a canocanil ABO reduction to the DBDH problem.
Due to space limitations, we omit the proof.
4.4 All-But-N Reductions
We can extend canonical ABO reductions to canonical all-but-N (ABN) reductions. Here, N is an a-priori bounded/unbounded polynomial of the security parameter. Roughly speaking, a canonical ABN reduction punctures N points \(\mathbf {t}^{*}= (t^{*}_1,\ldots ,t^{*}_N) \in \mathcal {T}^N\) in a master secret-key based algorithm \(\mathsf {MSKAlg}\) instead of a single point \(t^{*}\).
We omit the definition due to space limitations. Basically, we simply replace a single point \(t^{*}\) with N points \(\mathbf {t}^{*}=(t^{*}_1,\ldots ,t^{*}_N)\) and require \(\mathsf {Adml}(t^{*}_i,\mathsf {query})=\top \) for all \(i\in [N]\) for admissible queries. See the full version for details.
4.5 Concrete Examples of Canonical ABN Reductions
It is easy to extend ABO reductions to ABN reductions for pairing-based schemes by using (weak) programmable hash functions [26, 27]. Due to space limitations, we omit details. We can obtain the modified Boneh-Boyen IBE scheme, which has a canonical all-but-N reduction, by using programmable hash  where the hash key is \( (H_0,H_1,\ldots ,H_N)\) instead of the Boneh-Boyen hash function
where the hash key is \( (H_0,H_1,\ldots ,H_N)\) instead of the Boneh-Boyen hash function  where the hash key is \( (G_1,H)\).
where the hash key is \( (G_1,H)\).
The rough idea is as follows. The ABN reduction is given a DBDH instance \(\pi =(G,G^x,G^y,G^z,T)\) and target identities \(\mathbf {t}^{*}= \mathbf {\mathsf {id}}^* = (\mathsf {id}_1^*,\ldots ,\mathsf {id}_N^*)\), and simulates \(\mathsf {MPK}\). It chooses \(\mathsf {id}_0^* \leftarrow \mathbb {Z}_p\) and \((\beta _0,\ldots ,\beta _N) \leftarrow \mathbb {Z}_p^{N+1}\), and computes \((\alpha _0,\ldots ,\alpha _N)\) such that \(\sum _{i=0}^N \alpha _i \cdot t^i = \prod _{i=0}^N (t-\mathsf {id}^*_i) \in \mathbb {Z}_p[t]\). Then, it sets  ,
,  , and
, and  , and outputs
, and outputs  . By this parameter setting, we can implement canonical ABN reductions in a similar way to the ABO reduction of Boneh-Boyen IBE. See the full version for detail.
. By this parameter setting, we can implement canonical ABN reductions in a similar way to the ABO reduction of Boneh-Boyen IBE. See the full version for detail.
5 Message-Less Watermarking via Canonical ABO-reductions
In this section, we present a message-less watermarking scheme from all-but-one reductions. We focus on using canonical ABO reductions for the decisional case. It is easy to adapt that for the computational case, so we omit it.
First, we present our watermarking scheme \(\mathsf {WM}_\varSigma \,{ =}\,(\mathsf {WM}\mathsf {Setup},\mathsf {Mark},\mathsf {Extract})\) for \(\varSigma \). Let \(\mathsf {MSK}\) be a master secret-key generated by the setup algorithm of \(\varSigma \). \(\mathsf {WM}_\varSigma \) is a public mark and public extraction scheme. Thus, we do not need watermarking secret-key \(\mathsf {wsk}\).
-
\(\mathsf {WM}\mathsf {Setup}(1^\lambda )\):
-
Choose \(t^{*}\leftarrow \mathcal {T}\) and output
 .
.
-
-
\(\mathsf {Mark}(\mathsf {wpp},\mathsf {MSK})\):
-
Read \(\mathsf {MSK}\) and generate \((\pi ',\rho ') \leftarrow \mathsf {MSKtoP}(1^\lambda ,\mathsf {MSK},t^{*})\).
-
Generate a circuit \(\widetilde{f}_\varSigma [\pi ',\rho ',t^{*}]\) described in Fig. 3.
-
-
\(\mathsf {Extract}(\mathsf {wpp},\mathsf {PP},C')\):
-
Choose \(\mathsf {query}\leftarrow \mathcal {Q}\) such that \(\mathsf {Adml}(t^{*},\mathsf {query}) = \top \).
-
Sample \(\rho _{{\mathsf{o}}}\leftarrow \mathcal {R}_{\mathsf {mka}}\) and compute \(\mathsf {answer}_{} \leftarrow C'(\mathsf {query}_{},\rho _{{\mathsf{o}}})\).
-
Check \(\mathsf {Valid}(\mathsf {PP},\mathsf {query}_{},\mathsf {answer}_{}) {\mathop {=}\limits ^{\mathrm {?}}}\top \). If the equation holds, then output \(\mathsf {unmarked}\). Otherwise, \(\mathsf {marked}\).
-
Remark 5.1
Even a useless circuit that outputs \(\bot \) for all inputs is marked in the watermarking scheme above since \(\mathsf {Valid}(\mathsf {PP},\mathsf {query},\rho _{\mathsf{q}},\bot )=\bot \) for any \(\mathsf {PP}\), \(\mathsf {query}\), and \(\rho _{\mathsf{q}}\). To prevent this trivial watermarking, we need to check whether a circuit is similar to a master secret-key based algorithm whose corresponding master public parameter is \(\mathsf {PP}\). Although we omit this checking procedure for simplicity here (our final goal is achieving message-embedding schemes), we present test algorithms for this check in Sect. 6.
Theorem 5.1
Let \(\varSigma \) be a master secret-key based scheme with \((\mathcal {T},\mathcal {Q},\mathcal {P},\mathcal {R}_{\mathsf {mka}})\) associated with sub-query space \(\mathcal {Q}_\mathsf {t}\), aux-query space \(\mathcal {Q}_\mathsf {aux}\), challenge space \(\mathcal {H}\), challenge answer space \(\mathcal {I}\), and admissible condition \(\mathsf {Adml}\). If \(\varSigma \) has a canonical all-but-one reduction to a hard problem \(\varPi \), then there exists a message-less watermarking scheme \(\mathsf {WM}_\varSigma \) for master secret-keys of \(\varSigma \) and \(\mathsf {WM}\) satisfies Definition 3.5 with parameter \(\epsilon = 1/{\mathrm {poly}}(\lambda )\) under the assumption that \(\varPi \) is hard.
The intuition of security is that adversaries cannot recover the functionality of \(\mathsf {MSKAlg}(\mathsf {MSK},\cdot )\) for input \(t^{*}\) from the oracle simulation algorithm \(\mathsf {OSim}\) since \(\mathsf {OSim}\) is punctured at \(t^{*}\) (explained in Sect. 1.3). Due to space limitations, we omit the proof.
6 Message-Embedding Watermarking via Canonical ABN-reductions
In this section, we present a message-embedding watermarking scheme from canonical all-but-N reductions.
6.1 How to Test Circuit Similarity
Before we describe our message-embedding watermarking scheme, we present how to test a circuit is similar to the original circuit to be watermarked.
Test Circuits by Master Public Parameters. We define test algorithms \(\mathsf {Test}\) described in Fig. 4 to verify that a circuit \(C'\) is close to a master secret-key based algorithm whose master secret key is \(\mathsf {MSK}\) that corresponds to a master public parameter \(\mathsf {PP}\). We have two versions of \(\mathsf {Test}\) since there are a few differences between one for signature/IBE/ABE/IPE/PE and one for TBE. However, we omit that of TBE due to space limitations. We set parameters \(0<\epsilon _1< \epsilon _2 < 1/2\) where \(\epsilon _2 - \epsilon _1 > 1/{\mathrm {poly}}(\lambda )\).
Theorem 6.1
Assume that \(0<\epsilon _1< \epsilon _2 < 1/2\) where \(\epsilon _2 - \epsilon _1 > 1/{\mathrm {poly}}(\lambda )\). For all \((\mathsf {PP},\mathsf {MSK})\leftarrow \mathsf {PGen}(1^\lambda )\),
-
For all \(C'(\cdot ,\cdot ) \cong _{\epsilon _1} \mathsf {MSKAlg}(\mathsf {MSK},\cdot ;\cdot )\), \(\Pr [\mathsf {Test}(\mathsf {PP},C')=\top ] \ge 1 - {\mathsf {negl}}(\lambda )\).
-
For all \(C'(\cdot ,\cdot ) \not \cong _{\epsilon _2} \mathsf {MSKAlg}(\mathsf {MSK},\cdot ;\cdot )\), \(\Pr [\mathsf {Test}(\mathsf {PP},C')=\top ] \le {\mathsf {negl}}(\lambda )\).
We omit the proof due to space limitations.
By the theorem, we can verify whether \(C'(\cdot ,\cdot ) \cong _{\epsilon _1} \mathsf {MSKAlg}(\mathsf {MSK},\cdot ;\cdot )\) or not if \(\epsilon _1 = 1/2 - 1/{\mathrm {poly}}(\lambda )\). That is, if the adversary \(\mathcal {A}\) in \(\epsilon \)-unremovability game is \(\epsilon \)-admissible where \(\epsilon = 1/2 +1/{\mathrm {poly}}(\lambda )\), then the circuit \(C^*\) output by \(\mathcal {A}\) passes the test.
6.2 Message-Embedding Scheme
We present our message-embedding watermarking scheme \(\mathsf {msWM}_\varSigma =(\mathsf {WM}\mathsf {Setup},\mathsf {Mark},\mathsf {Extract})\) for \(\varSigma \). We consider none of ABE, IPE, and PE for the message-embedding scheme since we do not have (canonical) ABN reductions of them. Thus, \(\mathcal {T}= \mathcal {Q}_\mathsf {t}\) in the rest of this section. Note that we implicitly assume that the master secret key \(\mathsf {MSK}\) of \(\varSigma \) includes the corresponding public parameter \(\mathsf {PP}\). We use a PRF \((\mathsf {PRF}.\mathsf {Gen},\mathsf {PRF}.\mathsf {Eval})\) such that \(\mathsf {PRF}.\mathsf {Eval}(\mathsf {K},\cdot ): \{0,1\}^{|\mathsf {PP}|} \times [\ell ] \times \{0,1\}^{} \rightarrow \mathcal {T}^{T}\). We show only for the decisional case, but it is easy to adapt to the computational case.
-
\(\mathsf {WM}\mathsf {Setup}(1^\lambda )\):
-
Let
 .
. -
Generate \(\mathsf {K}\leftarrow \mathsf {PRF}.\mathsf {Gen}(1^\lambda )\) and set
 and
and 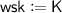 . We omit \(\mathsf {wpp}\) hereafter since it is \(\bot \).
. We omit \(\mathsf {wpp}\) hereafter since it is \(\bot \).
-
-
\(\mathsf {Mark}(\mathsf {wsk},\mathsf {MSK},\omega )\):
-
Compute \(\varvec{t}_i = (t_{i}^{(1)},\ldots ,t_{i}^{(T)}) \leftarrow \mathsf {PRF}.\mathsf {Eval}(\mathsf {K},(\mathsf {PP},i,\omega _i))\) for \(i\in [\ell ]\) and set
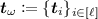 .
. -
Read \(\mathsf {MSK}\) and generate \((\pi ',\rho ') \leftarrow \mathsf {MSKtoP}(1^\lambda ,\mathsf {MSK},\varvec{t}_\omega )\).
-
Generate a circuit \(\widetilde{f}_\varSigma [\pi ',\rho ',\varvec{t}_\omega ]\) described in Fig. 5.
-
-
\(\mathsf {Extract}(\mathsf {wsk},\mathsf {PP},C')\):
-
Compute \(b_\mathsf {PP}\leftarrow \mathsf {Test}(\mathsf {PP},C')\). If \(b_\mathsf {PP}= \bot \), then output \(\texttt {Invalid-Key}\) and halt. Otherwise, do the following steps.
-
Compute \(\varvec{\widetilde{t}}_{i,b} = (\widetilde{t}_{i,b}^{(1)},\ldots ,\widetilde{t}_{i,b}^{(T)}) \leftarrow \mathsf {PRF}.\mathsf {Eval}(\mathsf {K},(\mathsf {PP},i,b))\) for \(i\in [\ell ]\) and \(b\in \{0,1\}^{}\).
-
For \(i \in [\ell ]\), \(b\in \{0,1\}\), set
 , compute \(\mathsf {answer}_{i,b}^{(j)} \leftarrow C'(\mathsf {query}_{i,b}^{(j)},\rho _{{\mathsf{o}},j})\). Let \(\widehat{N}_{i,b}\) be the number of indices \(j\in [T]\) such that \(\mathsf {Valid}(\mathsf {PP},\mathsf {query}_{i,b}^{(j)},\mathsf {answer}_{i,b}^{(j)}) = \bot \).
, compute \(\mathsf {answer}_{i,b}^{(j)} \leftarrow C'(\mathsf {query}_{i,b}^{(j)},\rho _{{\mathsf{o}},j})\). Let \(\widehat{N}_{i,b}\) be the number of indices \(j\in [T]\) such that \(\mathsf {Valid}(\mathsf {PP},\mathsf {query}_{i,b}^{(j)},\mathsf {answer}_{i,b}^{(j)}) = \bot \).-
If there exists an index \(i\in [\ell ]\) where \(\widehat{N}_{i,0}, \widehat{N}_{i,1} < T \) or \(\widehat{N}_{i,0}=\widehat{N}_{i,1} = T\), then output \(\bot \).
-
Otherwise, for each \(i\in [\ell ]\), let \(\omega '_i \in \{0,1\}\) be the unique bit where \(\widehat{N}_{i,\omega '_i} = T \wedge \widehat{N}_{i,1-\omega '_i} < T\) and output
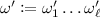 .
.
-
-
Theorem 6.2
Let \(\varSigma \) be a master secret-key based scheme with \((\mathcal {T},\mathcal {Q},\mathcal {P},\mathcal {R}_{\mathsf {mka}})\) associated with challenge space \(\mathcal {H}\), challenge answer space \(\mathcal {I}\), and admissible condition \(\mathsf {Adml}\). If \(\varSigma \) has a canonical all-but-N reduction to a hard problem \(\varPi \) and \(\mathsf {PRF}\) is a PRF where \(N = \ell \lambda \), then there exists a message-embedding watermarking scheme \(\mathsf {msWM}_\varSigma \) for master secret keys of \(\varSigma \) and \(\mathsf {msWM}_\varSigma \) satisfies Definition 3.5 with parameter \(\epsilon = 1/2 + 1/{\mathrm {poly}}(\lambda )\) under the assumption that \(\varPi \) is hard.
Due to space limitations, we omit the proof.
Notes
- 1.
If a car owner can directly install a PRF key into a car, and a watermarking scheme is public marking type, then watermarkable PRFs work in this scenario. However, this situation is not preferable.
- 2.
If a watermarking scheme is secret marking type, then we run a secure two-party computation between a user and a manufacturer.
- 3.
- 4.
See Sect. 4.2 for the formal definition and the meaning of “canonical”.
- 5.
There is no general conversion from ABO to ABN reductions, but upgrading is possible for many concrete schemes by using programmable hash. See Sect. 4.5 for more detail.
- 6.
In adaptive security games, adversaries can select the target at any time.
- 7.
A useless circuit that outputs \(\bot \) for all inputs is watermarked by this detection. To prevent this, we test the functionalities of circuits. See Sect. 6 for details.
- 8.
We do not explain how to determine \(\mathsf {m}^*\) here since it is not essential in this overview.
- 9.
All-but-N reductions should be able to generate N simulated challenge ciphertexts in the encryption case. This simulation is easy to achieve by using random self-reducibility of underlying hard problems for the discrete-logarithm-based case. In the LWE case, polynomially many (so, N) problem instances can be given.
- 10.
We do not consider constructions from strong assumptions such as IO in this study.
- 11.
We focus on constructions in the standard model in this paper. If we instantiate a signature scheme with Schnorr signature scheme [41], GKM+SIG would be more efficient.
- 12.
Collusion-resistant watermarkable signatures may have an application to group signatures. However, the application is non-trivial since we should be able to trace users from signatures (not from signing keys) in the group signature setting.
- 13.
- 14.
Jumping ahead, \(\mathcal {T}\) is a space where adversaries select targets at the beginning of security games.
- 15.
ePrint archive report 2019/628, Section 3.4 and C.4 (version 20190908).
References
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_28
Agrawal, S., Boyen, X., Vaikuntanathan, V., Voulgaris, P., Wee, H.: Functional encryption for threshold functions (or Fuzzy IBE) from lattices. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 280–297. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30057-8_17
Agrawal, S., Freeman, D.M., Vaikuntanathan, V.: Functional encryption for inner product predicates from learning with errors. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 21–40. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_2
Ananth, P., Vaikuntanathan, V.: Optimal bounded-collusion secure functional encryption. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019, Part I. LNCS, vol. 11891, pp. 174–198. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36030-6_8
Attrapadung, N., Hanaoka, G., Yamada, S.: New security proof for the Boneh-Boyen IBE: tight reduction in unbounded multi-challenge security. In: Hui, L.C.K., Qing, S.H., Shi, E., Yiu, S.M. (eds.) ICICS 2014. LNCS, vol. 8958, pp. 176–190. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21966-0_13
Attrapadung, N., Libert, B.: Functional encryption for inner product: achieving constant-size ciphertexts with adaptive security or support for negation. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 384–402. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_23
Baldimtsi, F., Kiayias, A., Samari, K.: Watermarking public-key cryptographic functionalities and implementations. In: Nguyen, P., Zhou, J. (eds.) ISC 2017. LNCS, vol. 10599, pp. 173–191. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-69659-1_10
Barak, B., et al.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6 (2012)
Boneh, D., Boyen, X.: Efficient selective identity-based encryption without random oracles. J. Cryptol. 24(4), 659–693 (2011). https://doi.org/10.1007/s00145-010-9078-6
Boneh, D., et al.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_30
Boneh, D., Hamburg, M.: Generalized identity based and broadcast encryption schemes. In: Pieprzyk, J. (ed.) ASIACRYPT 2008. LNCS, vol. 5350, pp. 455–470. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89255-7_28
Boneh, D., Lewi, K., Wu, D.J.: Constraining pseudorandom functions privately. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10175, pp. 494–524. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_17
Boyen, X., Mei, Q., Waters, B.: Direct chosen ciphertext security from identity-based techniques. In: ACM CCS (2005)
Boneh, D., Sahai, A., Waters, B.: Fully collusion resistant traitor tracing with short ciphertexts and private keys. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 573–592. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_34
Cash, D., Hofheinz, D., Kiltz, E., Peikert, C.: Bonsai trees, or how to delegate a lattice basis. J. Cryptol. 25(4), 601–639 (2012). https://doi.org/10.1007/s00145-011-9105-2
Chen, J., Lim, H., Ling, S., Wang, H., Wee, H.: Shorter identity-based encryption via asymmetric pairings. Des. Codes Cryptogr. 73(3), 911–947 (2014). https://doi.org/10.1007/s10623-013-9834-3
Chor, B., Fiat, A., Naor, M.: Tracing traitors. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 257–270. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_25
Cohen, A., Holmgren, J., Nishimaki, R., Vaikuntanathan, V., Wichs, D.: Watermarking cryptographic capabilities. Cryptology ePrint Archive, Report 2015/1096
Cohen, A., Holmgren, J., Nishimaki, R., Vaikuntanathan, V., Wichs, D.: Watermarking cryptographic capabilities. SIAM J. Comput. 47(6), 2157–2202 (2018)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. J. ACM 62(6), 45:1–45:33 (2015)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_25
Goyal, R., Kim, S., Manohar, N., Waters, B., Wu, D.J.: Watermarking public-key cryptographic primitives. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 367–398. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_12
Goyal, R., Koppula, V., Waters, B.: Collusion resistant traitor tracing from learning with errors. In:50th ACM STOC (2018)
Goyal, R., Koppula, V., Waters, B.: New approaches to traitor tracing with embedded identities. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11892, pp. 149–179. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36033-7_6
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: ACM CCS (2006)
Hofheinz, D., Jager, T., Kiltz, E.: Short signatures from weaker assumptions. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 647–666. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_35
Hofheinz, D., Kiltz, E.: Programmable hash functions and their applications. J. Cryptol. 25(3), 484–527 (2012). https://doi.org/10.1007/s00145-011-9102-5
Hopper, N., Molnar, D., Wagner, D.: From weak to strong watermarking. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 362–382. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_20
Katsumata, S., Nishimaki, R., Yamada, S., Yamakawa, T.: Designated verifier/prover and preprocessing NIZKs from Diffie-Hellman assumptions. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 622–651. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_22
Katsumata, S., Nishimaki, R., Yamada, S., Yamakawa, T.: Exploring constructions of compact NIZKs from various assumptions. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 639–669. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_21
Kiltz, E.: Chosen-ciphertext security from tag-based encryption. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 581–600. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_30
Kim, S., Wu, D.J.: Watermarking cryptographic functionalities from standard lattice assumptions. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 503–536. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_17
Kim, S., Wu, D.J.: Watermarking PRFs from lattices: stronger security via extractable PRFs. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 335–366. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_11
Kurosawa, K., Trieu Phong, L.: Leakage resilient IBE and IPE under the DLIN assumption. In: Jacobson, M., Locasto, M., Mohassel, P., Safavi-Naini, R. (eds.) ACNS 2013. LNCS, vol. 7954, pp. 487–501. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38980-1_31
Naccache, D., Shamir, A., Stern, J.P.: How to copyright a function? In: Imai, H., Zheng, Y. (eds.) PKC 1999. LNCS, vol. 1560, pp. 188–196. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-49162-7_14
Nishimaki, R.: How to watermark cryptographic functions by bilinear maps. IEICE Trans. 102–A(1), 99–113 (2019)
Nishimaki, R., Wichs, D., Zhandry, M.: Anonymous traitor tracing: how to embed arbitrary information in a Key. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 388–419. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_14
Quach, W., Wichs, D., Zirdelis, G.: Watermarking PRFs under standard assumptions: public marking and security with extraction queries. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11240, pp. 669–698. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03810-6_24
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: 46th ACM STOC (2014)
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Schnorr, C.: Efficient signature generation by smart cards. J. Cryptol. 4(3), 161–174 (1991). https://doi.org/10.1007/BF00196725
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_7
Waters, B.: Ciphertext-policy attribute-based encryption: an expressive, efficient, and provably secure realization. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 53–70. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_4
Yang, R., Au, M.H., Lai, J., Xu, Q., Yu, Z.: Collusion resistant watermarking schemes for cryptographic functionalities. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019. LNCS, vol. 11921, pp. 371–398. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34578-5_14
Yoshida, M., Fujiwara, T.: Toward digital watermarking for cryptographic data. IEICE Trans. 94–A(1), 270–272 (2011)
Acknowledgments
The author would like to thank Fuyuki Kitagawa for valuable discussion and insightful comments on watermarking. The author also thanks Shuichi Katsumata and Shota Yamada for answering questions about lattices and programmable hash functions, and TCC 2020 reviewers for very constructive comments on the presentation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Nishimaki, R. (2020). Equipping Public-Key Cryptographic Primitives with Watermarking (or: A Hole Is to Watermark). In: Pass, R., Pietrzak, K. (eds) Theory of Cryptography. TCC 2020. Lecture Notes in Computer Science(), vol 12550. Springer, Cham. https://doi.org/10.1007/978-3-030-64375-1_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-64375-1_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64374-4
Online ISBN: 978-3-030-64375-1
eBook Packages: Computer ScienceComputer Science (R0)







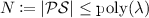 , for all
, for all 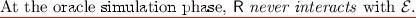
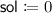 if
if  .
.


 .
. .
.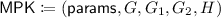 and
and 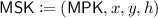 .
. .
. .
. ,
, 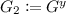 , and
, and  , and outputs
, and outputs  . The randomness
. The randomness 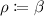

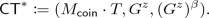

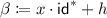 . Then, it outputs
. Then, it outputs  and
and 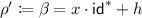 .
.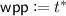 .
.

 .
. and
and 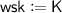 . We omit
. We omit 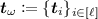 .
. , compute
, compute 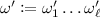 .
.
