Abstract
We present a computer-verified formalization of the post-quantum security proof of the Fujisaki-Okamoto transform (as analyzed by Hövelmanns, Kiltz, Schäge, and Unruh, PKC 2020). The formalization is done in quantum relational Hoare logic and checked in the qrhl-tool (Unruh, POPL 2019).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In this paper, we present the first formal verification of the post-quantum security of the Fujisaki-Okamoto transform.
Cryptographic security proofs tend to be complex, and, due to their complexity, error prone. Small mistakes in a proof can be difficult to notice and may invalidate the whole proof. For example, the proof of the OAEP construction [7] went through a number of fixes [13, 14, 27] until it was finally formally proven in [4] after years of industrial use. The PRF/PRP switching lemma was a standard textbook example for many years before it was shown that the standard proof is flawed [8]. And more recently, an attack on the ISO standardized blockcipher mode OCB2 [19] was found [18], even though OCB2 was believed to be proven secure by [24].
While a rigorous and well-structured proof style (e.g., using sequences of games as advocated in [8, 28]) can reduce the potential for hidden errors and imprecisions, it is still very hard to write a proof that is 100% correct. (Especially when proof techniques such as random oracles [9] or rewinding [30, 36] are used.) And especially if a mistake in a proof happens in a step that seems very intuitive, it is quite likely that the mistake will also not be spotted by a reader.
This problem is exacerbated in the case of post-quantum security (i.e., security against quantum adversaries): Post-quantum security proofs need to reason about quantum algorithms (the adversary). Our intuition is shaped by the experience with the classical world, and it is easy to have a wrong intuition about quantum phenomena. This makes it particularly easy for seemingly reasonable but incorrect proof steps to stay undetected in a post-quantum security proof.
In a nutshell, to ensure high confidence in a post-quantum security proof, it is not sufficient to merely have it checked by a human. Instead, we advocate formal (or computer-aided) verification: the security proof is verified by software that checks every proof step. In this paper, we present the first such formal verification, namely of a variant of the Fujisaki-Okamoto transform [12] as analyzed by Hövelmanns, Kiltz, Schäge, and Unruh [17].
Post-Quantum Security. Quantum computers have long been known to be a potential threat to cryptographic protocols, in particular public key encryption. Shor’s algorithm [26] allows us to efficiently solve the integer factorization and discrete logarithm problems, thus breaking RSA and ElGamal and variants thereof. This breaks all commonly used public key encryption and signature schemes. Of course, as of today, there are no quantum computers that even come close to being able to execute Shor’s algorithm on reasonable problem sizes. Yet, there is constant progress towards larger and more powerful quantum computers (see, e.g., the recent breakthrough by Google [2]). In light of this, it is likely that quantum computers will be able to break today’s public key encryption and signature schemes in the foreseeable future. Since the development, standardization, and industrial deployment of a cryptosystem can take many years, we need to develop and analyze future post-quantum secure protocols already today. One important step in this direction is the NIST post-quantum competition [23] that will select a few post-quantum public-key encryption and signature schemes for industrial standardization.
Quantum Random Oracles. One important proof technique in cryptography are random oracles [6]. In a proof in the random oracle model, we idealize hash functions by assuming that every hash function is simply a uniformly random function. (All algorithms including the adversary get oracle access to that function.) Based on this assumption, security proofs become considerably simpler. In some cases, we only know security proofs in the random oracle model. Of course, this comes at a cost: This assumption is an idealization; concluding that a protocol that is secure in the random oracle model is also secure using a real-world hash function is merely a heuristic argument. (And this heuristic is known to be false in certain contrived cases, e.g., [11].)
As first explicitly pointed out by [9], in the quantum setting, the random oracle becomes more involved: To get a realistic modeling, the adversary needs to be given superposition access to the random oracle, i.e., the adversary can evaluate the random oracle/hash function in a quantum superposition of many possible inputs. Due to this, quantum random oracle proofs are much harder than in the classical setting.
Of importance for this paper is the O2H theorem [1]. The O2H theorem tells us – very roughly – that the probability of noticing whether a specific output H(x) of the random oracle has been changed (“reprogrammed”) can be bounded in terms of the probability of guessing that input x. This technique is used in a number of QROM proofs, in particular those for the FO transform described next.
Fujisaki-Okamoto. A common approach for constructing public key encryption schemes is the Fujisaki-Okamoto (FO) transform [12] or a variant thereof. The FO transform takes a public-key encryption scheme with some weak passive security notion (such as IND-CPA or one-way security) and transforms it into an actively secure public-key encryption or KEMFootnote 1 scheme (IND-CCA security). On a very high level, instead of executing the encryption algorithm with true randomness, the FO transform hashes the plaintext and uses the resulting hash value as the randomness for the encryption algorithm. This removes some of the flexibility the attacker has when constructing fake ciphertexts and makes chosen-ciphertext attacks impossible. The advantage of the FO transform is that it gets us IND-CCA security at no or almost no increase in ciphertext size or computational cost. The disadvantage is that the FO transform is only proven in the random oracle model, which means that there is a heuristic element to its security proof. Due to its high efficiency, the FO transform or some variations thereof is used in basically all public key encryption candidates in the NIST competition. Because of this, it is very important to understand the post-quantum security of the FO transform. However, due to the intricacies of the quantum random oracle model, proving the security of the FO transform is not as easy as in the classical setting. The first positive result was made by Ebrahimi Targhi and Unruh [29] who proved the security of an FO variant that includes one more hash value in the ciphertext. That result was adapted by [15] to several other FO variants, but still using an additional hash. ([15] also gives an excellent overview over the different FO variants.) The first result to prove post-quantum security of FO without an additional hash was given by Saito, Xagawa, and Yamakawa [25]. To achieve this, they introduced a new intermediate security notion called “disjoint simulatability”. However, [25] relies on the assumption that the underlying passively-secure encryption scheme has perfect correctness, i.e., the probability of incorrectly decrypting honestly generated ciphertexts is zero. Unfortunately, this is not the case with typical lattice-based encryption schemes (they have a negligible failure probability), making the results of [25] inapplicable to many relevant encryption schemes such as, to the best of our knowledge, all lattice-based NIST candidates. This situation was resolved by Hövelmanns, Kiltz, Schäge, and Unruh [17] who show the security of an FO variant (without additional hash) that is secure even in the presence of decryption failures. (This result is the one we formalize in this work. We will refer to [17], specifically to the part concerned with the FO transformation, as HKSU in the following.)
Formal Verification of Cryptography. As mentioned above, a state-of-the-art approach for writing cryptographic security proofs are sequences of games. This approach is also well suited for formal verification. A number of frameworks/tools use this approach for verifying classical cryptography, e.g., EasyCrypt [3]. EasyCrypt requires the user to explicitly specify the games that constitute the security proof (as is done in a pen-and-paper proof), and to additionally provide justification for the fact that two consecutive games are indeed related as claimed. This justification will often be considerably more detailed than in a pen-and-paper proof where the fact that two slightly different games are equivalent will often be declared to be obvious.
Their approach for proving the relationship of consecutive games is to give a proof in relational Hoare logic. Relational Hoare logic is a logic that allows us to express the relationship between two programs by specifying a relational precondition and a relational postcondition. A relational Hoare judgment of the form \(\{\mathsf A\}\varvec{{\mathfrak c}}\sim \varvec{{\mathfrak d}}\{\mathsf B\}\) intuitively means that if the variables of the programs \(\varvec{{\mathfrak c}}\) and \(\varvec{{\mathfrak d}}\) are related as described by the precondition \(\mathsf A\) before execution, and we execute \(\varvec{{\mathfrak c}}\) and \(\varvec{{\mathfrak d}}\), then afterwards their variables will be related as described by \(\mathsf B\). A very simple example would be \(\{{x_1\le x_2}\} x\leftarrow {x+1}\sim x\leftarrow {x+1}\{{x_1\le x_2}\}\). This means that if the variable x in the left program is smaller-equal than in the right one, and both programs increase x, then x in the left program will still be smaller-equal than in the right one. As this example shows, relational Hoare logic can express more complex relationships than simple equivalence of two games. This makes the approach very powerful. To reason about cryptography, one needs a variant of relational Hoare logic that supports probabilistic programs. Such a probabilistic relational Hoare logic (pRHL) was developed for this purpose by Barthe, Grégoire, and Zanella Béguelin [5]. EasyCrypt uses pRHL for proving the relationship between cryptographic games.
Formal Verification of Quantum Cryptography. When considering the verification of post-quantum cryptography, one might wonder whether the tools developed for classical cryptography may not already be sufficient. Unfortunately, this is not the case. The soundness of the existing tools is proven relative to classical semantics of the protocols and of the adversary. In fact, at least for EasyCrypt, Unruh [32] gave an explicit example of a protocol which can be shown secure in EasyCrypt but which is known not to be secure against quantum adversaries. For the purpose of verifying quantum cryptography, Unruh [32] introduced a generalization of pRHL, quantum relational Hoare logic (qRHL) that allows to prove relational statements about quantum programs. (We will describe qRHL in more detail in Sect. 2.) Unruh [32] also developed a tool qrhl-tool for reasoning in qRHL for the purpose of verifying quantum cryptography. However, except for a toy example, the post-quantum security of a very simple encryption scheme, to the best of our knowledge, no post-quantum security proof has been formally verified before this work. qrhl-tool uses a hybrid approach: Reasoning about qRHL judgments is hardcoded in the tool, but verification conditions (i.e., auxiliary subgoals, e.g., implications between invariants) are outsourced to the theorem prover Isabelle/HOL [22].
Our Contribution. In this work, we formally verified the security proof of the FO transformation from HKSU [17].Footnote 2 The FO-variant analyzed by HKSU is a state-of-the-art construction for building efficient public-key encryption schemes, and can be applied to many of the NIST submissions to get IND-CCA secure encryption schemes (e.g., Frodo [20] or Kyber [10]).
Our formalization follows the overall structure of HKSU (i.e., it uses roughly the same games) but introduces many additional intermediate games. (Altogether, our proof defines 136 programs, which covers games, oracles, and explicitly constructed adversaries in reductions.) The formalization has 3455 lines of proof in qRHL and 1727 lines of proof in Isabelle/HOL for auxiliary lemmas. (Not counting comments and blank lines or files autogenerated by search & replace from others.) We mostly follow the structure of HKSU (but in many places we need to do some adjustments to achieve the level of rigor required for formal verification). In the process, we identified a few best practices for doing proofs in qrhl-tool that we list in Sect. 2.4.
We furthermore extended the qrhl-tool with a tactic o2h that implements an application of the Semiclassical O2H Theorem [1]. This is needed in HKSU, but the O2H Theorem is often in post-quantum crypto proofs, so we expect this addition to be very useful for future verifications, too. (Details are given in the full version [35].)
Organization. In Sect. 2, we review qRHL and the qrhl-tool. In Sect. 3, we review the result and part of the proof from HKSU. In Sect. 4, we go through the parts of the formalization that make up the specification of the main result. In Sect. 5, we discuss the formal proof. We conclude in Sect. 6. The source code of the formalization is provided in [33]. A full version with additional details is available at [35].
2 Quantum Relational Hoare Logic
In this section, we give an overview of quantum relational Hoare logic (qRHL). We will not give formal definitions or a set of reasoning rules. For these, refer to [32]. Instead, our aim is to give an intuitive understanding of the logic that allows to understand (most of) the reasoning steps in our formalization.
2.1 Quantum While Language
qRHL allows us to reason about the relationship between quantum programs (that encode cryptographic games). The programs are written in a simple while language that has the following syntax (where \(\varvec{{\mathfrak c}}\) and \(\varvec{{\mathfrak d}}\) stand for programs):

The language distinguishes two kinds of variables, quantum and classical. In the above syntax, classical variables are denoted by \(\mathbf{x} \) and quantum variables by \(\mathbf{q}\). The command \(\mathbf{x} \leftarrow e\) evaluates the expression e (which can be any well-typed mathematical expression involving only classical variables) and assigns the value to \(\mathbf{x} \). In contrast \(\mathbf{x} \, \overset{\$}{\leftarrow }\, e\) evaluates e which is supposed to evaluate to a distribution \(\mathcal {D}\), and then samples the new value of \(\mathbf{x} \) according to \(\mathcal {D}\). If- and while-statements branch depending on a classical expression e.
To initialize quantum variables, we use \(\mathbf {q}_1\dots \mathbf {q}_n \, \overset{\mathsf {q}}{\leftarrow } \, e\). Here e is evaluated to return a quantum state (i.e., a classical expression returning the description of a quantum state). Then \(\mathbf{q} _1 \ldots \mathbf{q} _n\) are jointly initialized with that state. E.g., we can write \(\mathbf{q} \, \overset{\mathsf {q}}{\leftarrow } \, |\mathbf{x} \rangle \) (where \(\mathbf{x} \) is a classical bit variable) to initialize a quantum bit \( \mathbf{q} \).
Given an expression e that computes a unitary U, we use \(\mathbf {apply} \, e \, \mathbf {to}\, {\mathbf {q}_1 \ldots \mathbf {q}_n}\) to apply U jointly to \(\mathbf {q}_1 \ldots \mathbf {q}_n\). E.g., \(\mathbf {apply} \, {\mathsf {CNOT}} \, \mathbf {to} \, {\mathbf {q}_1 \mathbf {q}_2}\).
\(\mathbf {x} \, \leftarrow \, \mathbf {measure} \, { \mathbf {q}_1 \ldots \, \mathbf {q}_n} \, \mathbf {with} \, e\) evaluates e to get a description of a measurement, measures \(\mathbf {q}_1 \ldots \mathbf {q}_n\) jointly with that measurement and assigns the result to \(\mathbf{x} \). Typically, e might be something like computational_basis, denoting a computational basis measurement.
Finally, \({\{}{} \mathbf{local} \, V;\varvec{{\mathfrak c}}{\}}\) declares the variables V as local inside \(\varvec{{\mathfrak c}}\). (This is an extension of the language from [34].)
2.2 QRHL Judgements
Recall from the introduction that in relational Hoare logics, judgments are of the form \(\{\mathsf A\}\varvec{{\mathfrak c}}\sim \varvec{{\mathfrak d}}\{\mathsf B\}\) where \(\varvec{{\mathfrak c}},\varvec{{\mathfrak d}}\) are programs, and \(\mathsf A,\mathsf B\) are relational predicates (the pre- and postcondition). In particular, \(\{\mathsf A\}\varvec{{\mathfrak c}}\sim \varvec{{\mathfrak d}}\{\mathsf B\}\) means that if the variables of \(\varvec{{\mathfrak c}},\varvec{{\mathfrak d}}\) (jointly) satisfy \(\mathsf A\) before execution, then they (jointly) satisfy \(\mathsf B\) after execution.
Predicates. The same idea is used in qRHL but the concept of predicates becomes more complex because we want to express something about the state of quantum variables. In fact, predicates in qRHL are subspaces of the Hilbert space of all possible states of the quantum variables of the two programs. We will illustrate this by an example:
Say \(\mathbf {q}\) is a quantum variable in the first program \(\varvec{{\mathfrak c}}\). We refer to \(\mathbf {q}\) as \(\mathbf {q}_1 \) to distinguish it from a variable with the same name in program \(\varvec{{\mathfrak d}}\). Say we want to express the fact that \(\mathbf {q}_1\) is in state \(|{+}\rangle \). That means that the whole system (i.e., all quantum variables together), are in a state of the form \(|{+}\rangle _{\mathbf {q}_1 }\otimes |{\varPsi }\rangle _{\mathbf {vars}}\) where \(\mathbf {vars}\) are all other variables (of \(\varvec{{\mathfrak c}}\) and \(\varvec{{\mathfrak d}}\)), except \(\mathbf {q}_1\). The set of all states of this form forms a subspace of the Hilbert space of all possible states of the quantum variables. Thus \(\mathsf A:=\{|{+}\rangle _{\mathbf {q}_1}\otimes |{\varPsi }\rangle _{\mathbf {vars}}:|{\varPsi }\rangle \in \mathcal {H}_{\mathbf {vars}}\}\) (with \(\mathcal {H}_{\mathbf {vars}}\) denoting the corresponding Hilbert space) is a subspace and thus a valid predicate for use in a qRHL judgment. For example, we could then write \(\{\mathsf A\}{\mathbf {apply}\, X \, \mathbf {to} \, \mathbf{q} }\,\sim \mathbf {skip}\{\mathsf A\}\) to express the fact that, if \( \mathbf{q} \) is in state \(|{+}\rangle \) in the left program, and we apply X (a quantum bit flip) to \( \mathbf{q} \), then afterwards q is still in state \(|{+}\rangle \). Of course, writing \(\mathsf A\) explicitly as a set is very cumbersome. (And, in the setting of formal verification, one would then have no syntactic guarantees that the resulting set is indeed a valid predicate.) Instead, we have the shorthand \(\text {span}\{ {|{+}\rangle }\}\) »\({\mathbf {q}_1}\) to denote the above predicate \(\mathsf A\). (More generally, S»\({\mathbf {q}_1 \dots \mathbf {q}_n}\) means that \({\mathbf {q}_1 \dots \mathbf {q}_n}\) are jointly in a state in S.)
We can build more complex predicates by combining existing ones. E.g., if \(\mathsf A,\mathsf A'\) are predicates, then \(\mathsf A\cap \mathsf B\) is a predicate that intuitively denotes the fact that both \(\mathsf A\) and \(\mathsf B\) hold. We will also often have to compare predicates. \(\mathsf A\subseteq \mathsf B\) means that \(\mathsf A\) is a subspace of \(\mathsf B\) for all values of the classical variables. Intuitively, this means \(\mathsf A\) implies \(\mathsf B\).
Predicates with Classical Variables. In most cases, however, we do not only have quantum variables, but also classical variables. Especially in a post-quantum cryptography setting, the majority of variables in a predicate tends to be classical. Support for classical variables in qRHL predicates is straightforward: A predicate \(\mathsf A\) can be an expression containing classical variables. Those are then substituted with the current values of those variables, and the result is a subspace that describes the state of the quantum variables as explained above. For example, we can write the predicate \(\texttt {span}\{|\mathbf{x _2}\rangle \}\) »\({\mathbf {q}_1}\). This would mean that \( q _1\) (a qubit in the left program) is in state \(|\mathbf{x _2}\rangle \).
This already allows us to build complex predicates, but it is rather inconvenient if we want to express something about the classical variables only, e.g., if we want to express that \(\mathbf{x} _1=\mathbf{x} _2\) always holds. To express such classical facts, we use an additional shorthand: \(\mathfrak {Cla}[ b]\) is defined to be \(\mathcal {H}\) (the full Hilbert space) if \(b=\mathtt {true}\), and defined to be 0 (the subspace containing only 0) if \(b=\mathtt {false}\). Why is this useful? Consider the predicate \(\mathfrak {Cla}[\mathbf{x _1=\mathbf{x} _2}]\). If \(\mathbf{x} _1=\mathbf{x} _2\), this evaluates to \(\mathfrak {Cla}[\mathtt {true}=\mathcal {H}]\). Since \(\mathcal {H}\) contains all possible states, the state of the quantum variables will necessarily be contained in \(\mathfrak {Cla}[\mathtt {true}]\), hence the predicate is satisfied. If \(\mathbf{x} _1\ne \mathbf{x} _2\), \(\mathfrak {Cla}[\mathbf{x _1=\mathbf{x} _2}]\) evaluates to \(\mathfrak {Cla}[\mathtt {false}=0]\), and the state of the quantum variables will not be contained in \(\mathfrak {Cla}[\mathtt {false}]\), hence the predicate will not be satisfied. Thus, \(\mathfrak {Cla}[\mathbf{x _1=\mathbf{x} _2}]\) is satisfied iff \(\mathbf{x} _1=\mathbf{x} _2\); the state of the quantum variables does not matter. In general \(\mathfrak {Cla}[ e]\) allows us to translate any classical predicate e into a quantum predicate. (And this predicate can then be combined with quantum predicates, e.g., \(\mathfrak {Cla}[\mathbf{x _1=\mathbf{x} _2}] \cap \texttt {span}\{|{+}\rangle \}\) »\({\mathbf {q}_1}\).)
Quantum Equality. One very important special case of predicates are equalities. We will often need to express that the variables of the left and right programs have the same values. We have already seen how to do this for classical variables. For quantum variables, the situation is more complex. We cannot write \(\mathfrak {Cla}[{\mathbf {q}_1= \mathbf {q}_2}]\), this is not even a meaningful expression (inside \(\mathfrak {Cla}[{\dots }]\), only classical variables are allowed). Instead, we need to define a subspace that in some way expresses the fact that two quantum variables are equal. The solution proposed in [32] is: Let \(\mathbf {q}_1\equiv _\mathsf {quant} \mathbf {q}_2\) denote the subspace of all states that are invariant under exchanging \(\mathbf {q}_1\) and \( \mathbf {q}_2\) (i.e., invariant under applying a swap operation). Then \(\mathbf {q}_1\equiv _\mathsf {quant} \mathbf {q}_2\) is a quantum predicate. And – this is less easy to see but shown in [32] – \(\mathbf {q}_1\equiv _\mathsf {quant} \mathbf {q}_2\) does indeed capture the idea that \(\mathbf {q}_1\) and \(\mathbf {q}_2\) have the same value in a meaningful way. We can now write, for example, \(\mathfrak {Cla}[\mathbf{x _1=\mathbf{x} _2}]\cap ({ \mathbf {q}_1\equiv _\mathsf {quant} \mathbf {q}_2})\) to denote the fact that the variables \(\mathbf{x} \) (classical) and q (quantum) have the same value in both programs. In particular, if \(\varvec{{\mathfrak c}}\) only contains those two variables, we have \(\{{\mathfrak {Cla}[\mathbf{x _1=\mathbf{x} _2}]\cap ({\mathbf {q}_1 \equiv _\mathsf {quant} \mathbf {q}_2})}\}\varvec{{\mathfrak c}}\sim \varvec{{\mathfrak c}} \{{\mathfrak {Cla}[\mathbf{x _1=\mathbf{x} _2}]\cap ({\mathbf {q}_1 \equiv _\mathsf {quant} \mathbf {q}_2})}\}\). What if there are more quantum variables? The advantage of the quantum equality is that we hardly ever need to recall the actual definition in terms of swap invariance. All we need to remember is that \( \mathbf {q}_1 \equiv _\mathsf {quant} \mathbf {q}_2\) is a quantum predicate/subspace that intuitively encodes equality of \(\mathbf {q}_1\) and \(\mathbf {q}_2\).
The most common form of predicate that we will see is \(\mathsf A_= := \mathfrak {Cla}[\mathbf{x ^{(1)}_1=\mathbf{x} ^{(1)}_2 \wedge \dots \wedge \mathbf{x} ^{(1)}_1=\mathbf{x} ^{(1)}_2}] \cap ({ \mathbf{q} ^{(1)}_1\dots \mathbf{q}^{(m)}_1\equiv _\mathsf {quant} \mathbf{q}^{(1)}_2\dots \mathbf{q}^{(m)}_2})\). In fact, if both sides have the same program \(\varvec{{\mathfrak c}}\) (and \(\varvec{{\mathfrak c}}\) contains no variables besides the ones mentioned in \(\mathsf A_=\)), then \(\{{\mathsf A_=}\}\varvec{{\mathfrak c}}\sim \varvec{{\mathfrak c}}\{{\mathsf A_=}\}\) holds. Intuitively, this means: if the inputs of two programs are equal, the outputs are equal.
2.3 Reasoning in qRHL
To derive qRHL judgments, one will hardly ever go directly through the definition of qRHL itself. Instead one derives complex qRHL judgments from elementary ones. For example, to derive the elementary \(\{{\mathfrak {Cla}[\mathbf{x _1=0}]}\}\mathbf{x \leftarrow \mathbf{x +1}}\sim {\mathbf {skip}}\{{\mathfrak {Cla}[\mathbf{x _1=1}]}\}\), we use the Assign1 rule [32] that states \(\{{\mathsf B\{e_1/\mathbf{x} _1\}}\}\mathbf{x \leftarrow e}\sim {\mathbf {skip}}\{\mathsf B\}\). (Here \(e_1\) is the expression e where all variables \(\mathbf {y}\) are replaced by \(\mathbf {y}_1\). And \(\mathsf B\{e_1/\mathbf{x} _1\}\) means every occurrence of \(\mathbf{x} _1\) in \(\mathsf B\) is replaced by \(e_1\).) With \(\mathsf B:= \mathfrak {Cla}[\mathbf{x _1=1}]\), we get from Assign1: \(\{{\mathfrak {Cla}[\mathbf{x _1+1=1}]}\}\mathbf{x \leftarrow e}\sim {\mathbf {skip}}\{{\mathfrak {Cla}[\mathbf{x _1= 1}]}\}\). Since \(\mathbf{x} _1+1=1\) is logically equivalent to \(\mathbf{x} _1=1\) (assuming the type of \(\mathbf{x} \) is, e.g., integers or reals), this statement is equivalent to \(\{{\mathfrak {Cla}[\mathbf{x _1=0}]}\}\mathbf{x \leftarrow \mathbf{x +1}}\sim {\mathbf {skip}}\{{\mathfrak {Cla}[\mathbf{x _1=1}]}\}\). (This is an example of reasoning in the “ambient logic”: Besides application of qRHL rules, we need to use “normal” mathematics to derive facts about predicates. This is external to qRHL itself.)
One can then combine several judgments into one, using, e.g., the Seq rule: “If \(\{\mathsf A\}\varvec{{\mathfrak c}}\sim \varvec{{\mathfrak d}}\{\mathsf B\}\) and \(\{\mathsf B\}{\varvec{{\mathfrak c}}'}\sim {\varvec{{\mathfrak d}}'}\{\mathsf C\}\) holds, then \(\{\mathsf A\}{\varvec{{\mathfrak c}};\varvec{{\mathfrak c}}'}\sim {\varvec{{\mathfrak d}};\varvec{{\mathfrak d}}'}\{\mathsf C\}\) holds.” For example, once we have derived \(\{{\mathfrak {Cla}[{\mathtt {true}}]}\}\mathbf{x \leftarrow 1}\sim \mathbf {skip}\{{\mathfrak {Cla}[\mathbf{x _1=1}]}\}\) and \(\{{\mathfrak {Cla}[\mathbf{x _1=1}]}\}\mathbf {skip}\sim {\mathbf {y}\leftarrow 1}\{{\mathfrak {Cla}[\mathbf{x _1=\mathbf {y}_2}]}\}\), we conclude using Seq that \(\{{\mathfrak {Cla}[{\mathtt {true}}]}\}\mathbf{x \leftarrow 1}\sim {\mathbf {y}\leftarrow 1}\{{\mathfrak {Cla}[\mathbf{x _1=\mathbf {y}_2}]}\}\). (We use here implicitly that \(\mathbf{x} \leftarrow 1;\mathbf {skip}\) is the same as \(\mathbf{x} \leftarrow 1\) and analogously for \(\mathbf {skip};\mathbf {y}\leftarrow 1\).)
We will not give the full list of rules here, see [32] and the manual of [31] for a comprehensive list.
One common approach to prove more complex qRHL judgments is backward reasoning: One starts by stating the judgment one wants to prove, say \(G_1:=\{{\mathfrak {Cla}[{\mathtt {true}}]}\}\mathbf{x \leftarrow 1}\sim {\mathbf {y}\leftarrow 1}\{{\mathfrak {Cla}[\mathbf{x _1=\mathbf {y}_2}]}\}\). Then one applies one qRHL rule to the very last statement on the left or right, say \(\mathbf {y}\leftarrow 1\). By application of the Seq and Assign2 rule, we see that \(G_2:=\{{\mathfrak {Cla}[{\mathtt {true}}]}\}\mathbf{x \leftarrow 1}\sim \mathbf {skip}\{{\mathfrak {Cla}[\mathbf{x _1=1}]}\}\) implies \(G_1\). So we have reduced our current goal to showing \(G_2\). (Using a reasoning step that can be fully automated.) By application of Seq and Assign1, we see that \(G_3:=\{{\mathfrak {Cla}[{\mathtt {true}}]}\}\mathbf {skip}\sim \mathbf {skip}\{{\mathfrak {Cla}[{1=1}]}\}\) implies \(G_2\). So our new proof goal is \(G_3\). And finally, \(G_3\) is implied by \(G_4:=({\mathfrak {Cla}[{\mathtt {true}}]\subseteq \mathfrak {Cla}[{1=1}]})\). So our final goal is \(G_4\) which is a trivial statement in ambient logic because \(1=1\) is \(\mathtt {true}\). Hence the proof concludes and \(G_1\) holds. The advantage of this approach is that it is fully mechanical in many cases, e.g., for sequences of assignments and applications of unitaries. The proof tool qrhl-tool (see the next section) follows exactly this approach.
So far, we have gotten a glimpse how to derive qRHL judgments. In a cryptographic proof, however, we are interested not in qRHL judgments but in statements about probabilities. Fortunately, we can derive those directly from a qRHL judgment using the QrhlElimEq rule. It states (somewhat simplified): Assuming \(\mathbf {X}\) and \(\mathbf {Q}\) are all the variables occurring in \(\varvec{{\mathfrak c}},\varvec{{\mathfrak d}}\), then \(\{{\mathfrak {Cla}[{\mathbf {X}_1=\mathbf {X}_2}]\cap ({\mathbf {Q}_1\equiv _\mathsf {quant}\mathbf {Q}_2})}\}\varvec{{\mathfrak c}}\sim \varvec{{\mathfrak d}} \{{\mathfrak {Cla}[{e_1\implies f_2}]}\}\) implies \(\Pr [e:\varvec{{\mathfrak c}}] \le \Pr [f:\varvec{{\mathfrak d}}]\) (and similarly for \(=\) instead of \(\le \)). (Here \(\Pr [e:\varvec{{\mathfrak c}}]\) denotes the probability that the Boolean expression e is true after executing \(\varvec{{\mathfrak c}}\), and analogously \(\Pr [f:\varvec{{\mathfrak d}}]\).) Thus to derive an inequality or equality of probabilities of program outcomes, we convert it into a qRHL proof goal with QrhlElimEq, and then use the reasoning rules of qRHL to derive that qRHL judgment. This is, on a high level, how crypto proofs in qRHL are done (modulo many concrete details).
2.4 The qrhl-tool
While reasoning using qRHL in pen-and-paper proofs is possible in principle, qRHL was specifically designed for formal verification on the computer. To that end, an interactive theorem prover for qRHL was developed, qrhl-tool [31, 32]. To execute our formalization, version 0.5 is required. See README.txt there for instructions on how to check/edit our formalization, and manual.pdf for detailed information. In the following, we recap the most important facts about the tool.
In addition to that review, we also list some “best practices” for developing proofs in the tool, based on our experience while formalizing HKSU.
Architecture of the Tool. qrhl-tool has a hybrid architecture: It embeds the theorem prover Isabelle/HOL, and all reasoning in the ambient logic is done by Isabelle/HOL. The tool handles qRHL judgments directly. As a consequence, proofs are written in two files: .thy files contain native Isabelle/HOL code and can reason only about ambient logic (no support for qRHL itself). Those .thy files are also used to specify the logical background of the formalization (e.g., declaring constants such as the encryption function in our development). .qrhl files are executed natively by qrhl-tool and contain specifications of programs, as well as proofs in qRHL. They can also contain proofs in ambient logic (arbitrary Isabelle/HOL tactics can be invoked) but this is only suitable for simple proofs in ambient logic. Complex ambient logic facts are best proven as an auxiliary lemma in the .thy files. It is possible to split a proof into many files by including one .qrhl file from another using the include command.
The tool can be run in two modes, batch and interactive mode. In batch mode, a given .qrhl file is checked on the command-line and the run aborts with an error if the proof is incorrect. In interactive mode, an Emacs/ProofGeneral-based user interface allows us to edit and execute the proofs.
Best practice: Create one file  that declares all program variables and loads the
that declares all program variables and loads the  files. Furthermore, create a separate file
files. Furthermore, create a separate file  for every declared program
for every declared program  , and a separate file
, and a separate file  for every lemma
for every lemma  . This allows us to execute proofs without too much runtime overhead and at the same time allows us to find quickly which entity is declared where. \(\diamond \)
. This allows us to execute proofs without too much runtime overhead and at the same time allows us to find quickly which entity is declared where. \(\diamond \)
Declarations. All program variables that occur in any analyzed program need to be declared globally (even if the variable is used only as a local variable). This is done using classical/quantum/ambient var x : type where type is any type understood by Isabelle/HOL. (ambient var declares an unspecified constant value that can be used in programs and in ambient logic subgoals.) Programs are declared by program name := { code } where code is a quantum program as described in Sect. 2.1. For describing games this approach is sufficient, but when specifying adversaries or oracles or helper functions, we would like to define procedures that take arguments and have return values. Unfortunately, such procedure calls are not supported by the language underlying qRHL yet. What has to be done instead is to pass values to/from procedures via global variables. A program X can be invoked by another program using call X,Footnote 3 and we need to write the program X so that it communicates with the invoking program via global variables that are set aside for this purpose. While this approach is not very convenient, we found that with disciplined variable use, no bigger problems arise.
One highly important feature in more advanced cryptographic definitions and proofs are oracles. Roughly speaking, an oracle is a program O that is given as an argument to another program A, so that the other program can execute it whenever needed. (For example, an adversary A may get access to a decryption oracle \(\mathsf {Dec}\) that decrypts messages passed to it.) Programs that take oracles are supported by qrhl-tool. One can declare a program via, e.g., program prog(O1,O2) := {code} where code can contain, e.g., a call O1 statement. Then prog is a program that needs to be instantiated with oracles when invoked, e.g.: call prog(Enc,Dec).
Finally, to model adversaries we need to declare programs of unspecified code. (This then means that anything that is proven holds for any adversary.) The command adversary A declares an adversary A that can be invoked via call A. Additional arguments to the adversary command allow to specify global variables that the adversary may access, and whether A expects oracles.
Best practice: When declaring a program that is intended as a subroutine (e.g., an oracle or an adversary), make explicit which global variables are used as inputs/outputs to simulate procedure calls. (E.g., an adversary might be annotated with a comment “Input:  (ciphertext). Output:
(ciphertext). Output:  (guessed bit). Internal state:
(guessed bit). Internal state:  .”)
.”)
All variables (especially quantum variables) that are used that are not needed between consecutive invocations should be made local at the beginning of the program using the  program statement.
program statement.
When invoking a program taking an oracle (e.g.,  where
where  expects inputs/outputs in variables
expects inputs/outputs in variables  ), the input/output variables should be made local at that call. (E.g.,
), the input/output variables should be made local at that call. (E.g.,  ) Otherwise,
) Otherwise,  will not be able to determine that
will not be able to determine that  are not changed globally, even if the code of
are not changed globally, even if the code of  internally already contains a
internally already contains a  statement.
statement.
 can be used in interactive mode to check the list of variables used by a program.
can be used in interactive mode to check the list of variables used by a program.
Following these rules may make many proofs somewhat longer (due to additional boilerplate for removing  commands) but it removes a lot of potential for conflicts in variable use. (Especially with quantum variables: due to the idiosyncrasies of the quantum equality, any quantum variable used non-locally by a subprogram will have to be carried around explicitly in all quantum equalities.) \(\diamond \)
commands) but it removes a lot of potential for conflicts in variable use. (Especially with quantum variables: due to the idiosyncrasies of the quantum equality, any quantum variable used non-locally by a subprogram will have to be carried around explicitly in all quantum equalities.) \(\diamond \)
Note that qRHL did not initially support local variables. The addition of local variables to qrhl-tool and the corresponding theory [34] were prompted by our experiences in the present formalization. Without local variables, it becomes very difficult to maintain a larger formalization involving quantum equalities.
Proving Lemmas. Finally, to state a lemma one can either state a lemma in ambient logic (extended with syntax Pr[...] for talking about the results of program executions), or qrhl subgoals. The command lemma name: formula states the former, the command qrhl name: {precondition} call X; \(\scriptstyle \sim \) call Y; {postcondition} the latter. The syntax Pr[e : prog(rho)] denotes the probability that the Boolean expression e is true after running prog with initial quantum state rho. Most of the time we will thus state lemmas of the form Pr[b=1 : prog1(rho)] = Pr[b=1 : prog2(rho)] where rho is an ambient variable (meaning, the initial state is arbitrary). This can be converted into a qRHL subgoal using the tactic byqrhl (implementing the rule QrhlElimEq).
Once one has stated a qRHL proof goal, the proof proceeds via backwards reasoning as described in Sect. 2.3. For example, to remove the last assign statement from a goal (and rewrite the postcondition accordingly) as done in Sect. 2.3, one writes wp left/right (or wp n m for the last n/m statements on the left/right). Once all statements are gone (skip on both sides), the tactic skip replaces \(\{\mathsf A\}\mathbf {skip}\sim \mathbf {skip}\{\mathsf B\}\) by the ambient logic goal \(\mathsf A\subseteq \mathsf B\). Another important tactic is conseq pre/post: \(\mathsf C\) which replaces the current pre-/postcondition by \(\mathsf C\) (and adds a ambient logic subgoal to prove that this replacement is justified). This allows to clean up subgoals and increases readability. The tactic simp simplifies the current goal using the Isabelle/HOL simplifier.
Best practice: To make proofs more maintainable, before each tactic invocation add a comment which line of code it addresses. E.g.,  will always affect the last command of the left program. If that command is, e.g.,
will always affect the last command of the left program. If that command is, e.g.,  , add the comment
, add the comment  . This ensures that if a change in a program definition breaks an existing proof, it is easier to find out where the proof script went out of sync.
. This ensures that if a change in a program definition breaks an existing proof, it is easier to find out where the proof script went out of sync.
Additionally, at regular intervals add the tactic  commands where
commands where  is the current postcondition (possibly, but not necessarily simplified). This serves both as a documentation of the current state of the proof, and it makes maintenance easier because the proof will fail at the first point where the postcondition is not what was expected anymore (as opposed to failing at a later point). \(\diamond \)
is the current postcondition (possibly, but not necessarily simplified). This serves both as a documentation of the current state of the proof, and it makes maintenance easier because the proof will fail at the first point where the postcondition is not what was expected anymore (as opposed to failing at a later point). \(\diamond \)
Isabelle/HOL Micro Primer. For an introduction to Isabelle/HOL we recommend [21]. Here, we only give some minimal information to help reading the code fragments in the paper (Figs. 7, 8 and 9). This micro primer does not does not allow us to understand the definitions given in this paper in depth. In particular, to understand them in depth one needs to know the predefined constants in Isabelle/HOL and in the qrhl-tool. But with the syntax given here, it should at least be possible to make educated guesses about the meanings of the definitions.
All constants in Isabelle/HOL are typed. A function f taking arguments of types \(t_1,\dots ,t_n\) and returning t has type \(t_1\Rightarrow \dots \Rightarrow t_n\Rightarrow t\). To invoke \(\mathtt {f}\) with arguments \(a_1,\dots ,a_n\), we write \(\mathtt {f}\ a_1\ a_2\ \dots \ a_n\). (Not \(\mathtt {f}(a_1,\dots ,a_n)\).) To declare (axiomatically) the existence of a new constant \(\mathtt {c}\) of type type, we write

Here the optional facts are logical propositions that we assume about c. For example, we can declare the existence of a commutative binary operation op on natural numbers via

Instead of axiomatizing constants, we can also define them in terms of existing constants. This cannot introduce logical inconsistencies. The syntax for this is

Instead of \(=\) we can also write \(\leftrightarrow \) when defining a proposition (i.e., if the return type is bool). For example, if we wanted to define the operation op above as twice the sum of its arguments, we could write:

The parts before where are optional and will be inferred if necessary.
This summary of the operation of qrhl-tool does not, of course, replace a reading of the manual. However, it should give a first impression as well as help in reading Sects. 4–5.
3 Fujisaki-Okamato á la HKSU
In this section, we describe the FO variant analyzed by HKSU [17] and their proof. We stress that the proof we analyzed (and describe here) is the one from the earlier version [16] of HKSU, it has been rewritten since we started our formalization.
The goal of the FO transform is to transform an encryption scheme that is passively secure into a chosen-ciphertext secure key encapsulation mechanism (KEM). The variant analyzed by HKSU can be described modularly by consecutively applying three transformations (called \(\mathsf {Punc}\), \(\mathsf {T}\), and \(\mathsf {U}^{\not \bot }_m\)) to the passively secure encryption scheme.
3.1 Transformation \(\mathsf {Punc}\)
We start with a base public-key encryption scheme \((\mathsf {Keygen}_0,\mathsf {Enc}_0,\mathsf {Dec}_0)\) with message space \(\mathcal M_0\). We assume the base scheme to be IND-CPA secure. (We assume further that decryption is deterministic, but we do not assume that decryption succeeds with probability 1, or that decrypting a valid ciphertext returns the original plaintext with probability 1.)
The first step is to construct a scheme with disjoint simulatability (DS). DS security [25] means that there exists a fake encryption algorithm \(\overline{\mathsf {Enc}}\) that (without being given a plaintext) returns ciphertexts that are indistinguishable from valid encryptions of random messages, but that are guaranteed to be distinct from any valid ciphertext with high probability.
More precisely:
Definition 1 (Disjoint simulatability)
We call \((\mathsf {Keygen},\mathsf {Enc},\mathsf {Dec})\) with message space \(\mathcal {M}\) and randomness space \(\mathcal {R}\) DS secure iff for any quantum-polynomial-time A, \(|{\Pr [b=1:\mathsf {DS_{real}}]-\Pr [b=1:\mathsf {DS_{fake}}]}|\) is negligible, for the games defined in Fig. 1.
We say \((\mathsf {Keygen},\mathsf {Enc},\mathsf {Dec})\) is \(\varepsilon \)-disjoint iff for all possible public keys \( pk \), \(\Pr [{({\exists m\in \mathcal {M}, r\in \mathcal {R}.\ c=\mathsf {Enc}( pk ,m;r)})} : c\leftarrow \overline{\mathsf {Enc}}( pk )]\le \varepsilon \).
The transformation \(\mathsf {Punc}\) is very straightforward: The encryption scheme is not really modified (i.e., the resulting \(\mathsf {Keygen},\mathsf {Enc},\mathsf {Dec}\) are the same in the base scheme). But the message space is reduced by one element. I.e., we simply declare one plaintext \(\hat{m}\) as invalid, hence encryptions of that plaintext will be disjoint from valid ciphertexts, and thus we can produce fake encryptions \(\overline{\mathsf {Enc}}\) by encrypting \(\hat{m}\). We summarize \(\mathsf {Punc}\) in Fig. 2. The proof that the resulting scheme is both DS and IND-CPA secure is very straightforward, and we omit it here. (But we have formalized it, of course.)
Transformation \(\mathsf {Punc}\). Input scheme: \((\mathsf {Enc}_0,\mathsf {Dec}_0,\mathsf {Keygen}_0)\) with message space \(\mathcal M_0\). Output scheme: \((\mathsf {Enc},\mathsf {Dec},\mathsf {Keygen})\) with message space \(\mathcal M_0\) and fake encryption algorithm \(\overline{\mathsf {Enc}}\).
3.2 Transformation \(\mathsf {T}\)
Transformation \(\mathsf {Punc}\) gave us a DS secure encryption scheme \(\mathsf {Enc}\). However, as the starting point for the transformation \(\mathsf {U}^{\not \bot }_m\) below, we need a deterministic encryption scheme (that is still DS secure).
Transformation \(\mathsf {T}\) achieves this by a simple technique: Instead of running \(\mathsf {Enc}\) normally (i.e., \(\mathsf {Enc}( pk ,m;r)\) with r uniformly from the randomness space \(\mathcal {R}\)), the modified encryption algorithm \(\mathsf {Enc}'\) computes the randomness r from the message m as \(r:=G(m)\). Here G is a hash function (modeled as a random oracle).
Transformation \(\mathsf {T}\) also strengthens the decryption algorithm: The decryption algorithm resulting from \(\mathsf {T}\) rejects any invalid ciphertexts (i.e., any ciphertext that is not in the range of \(\mathsf {Enc}'\)). This is achieved by adding an extra check to the decryption algorithm \(\mathsf {Dec}'\): After decrypting a ciphertext c to m, m is reencrypted and compared with the ciphertext c. Since \(\mathsf {Enc}'\) is deterministic, this will always succeed for honestly generated ciphertexts, but it will always fail for invalid ones.
We summarize transformation \(\mathsf {T}\) in Fig. 3.
Transformation \(\mathsf {T}\). Input scheme: \((\mathsf {Enc},\mathsf {Dec},\mathsf {Keygen})\) with message space \(\mathcal {M}\) and fake encryption algorithm \(\overline{\mathsf {Enc}}\). Output scheme: \((\mathsf {Enc}',\mathsf {Dec}',\mathsf {Keygen}')\) with message space \(\mathcal {M}'\) and fake encryption algorithm \(\overline{\mathsf {Enc}'}\). \(G:\mathcal {M}\rightarrow \mathcal {R}\) is a hash function (modeled as a random oracle).
Security of Transformation \(\mathsf {T}\). HKSU shows the following:
Theorem 1
(DS security of \({\mathsf {Enc}}^{\prime }\), informal). If \(\mathsf {Enc}\) is \(\varepsilon \)-disjoint, so is \(\mathsf {Enc}'\). If \(\mathsf {Enc}\) is DS secure and IND-CPA secure, then \(\mathsf {Enc}'\) is DS secure.
(In HKSU, the result is given with concrete security bounds.)
The core idea of the proof is to show that the adversary cannot distinguish between uniform randomness (as used in \(\mathsf {Enc}\)) and randomness \(r:=G(m^*)\) where \(m^*\) is the challenge message (as used in \(\mathsf {Enc}'\)). This is shown by bounding the probability for guessing \(m^*\) and then using the Semiclassical O2H theorem [1] to bound the distinguishing probability.
We omit the proof from this exposition (we will focus on the more complex proof of transformation \(\mathsf {U}^{\not \bot }_m\) below). The full proof can be found in [16].
3.3 Transformation \(\mathsf {U}^{\not \bot }_m\)
Finally, the transformation \(\mathsf {U}^{\not \bot }_m\) takes the deterministic DS secure encryption scheme and transforms it into a KEM. In a KEM, we have an encapsulation algorithm \(\mathsf {Encaps}\) that, instead of accepting a plaintext as input, uses a random (symmetric) key K as plaintext (intended for use in a symmetric encryption scheme) and returns both that key and the ciphertext. (We stress that K must not be confused with the public/secret keys of the KEM.) And the decapsulation algorithm \(\mathsf {Decaps}\) takes the ciphertext and returns the key, like a decryption does.
The encapsulation algorithm constructed by transformation \(\mathsf {U}^{\not \bot }_m\) picks a uniform \(m\overset{\$}{\leftarrow }\mathcal {M}'\) and encrypts it (resulting in a ciphertext c). However, instead of using m directly as the symmetric key, the key is set to be \(K:=H(m)\). (Here H is a hash function modeled as a random oracle.)
Decapsulating c is straightforward: By decrypting c we get m back, and then we can compute the key \(K:=H(m)\). However, there is a subtlety in case of decryption failures: If \(m=\bot \), then \(\mathsf {Decaps}\) does not return \(\bot \), but instead returns a key K that is indistinguishable from one that would result from a successful decryption. (This is called “implicit rejection”, as opposed to “explicit rejection” that would return \(\bot \).) This key K is generated from the ciphertext as \(K:=\mathsf {PRF}(k,c)\) where \(\mathsf {PRF}\) is a pseudorandom function.Footnote 4 And the PRF-key k is part of the secret key of the KEM. We describe the transformation \(\mathsf {U}^{\not \bot }_m\) in Fig. 4.
Transformation \(\mathsf {U}^{\not \bot }_m\). Input scheme: \((\mathsf {Enc}',\mathsf {Dec}',\mathsf {Keygen}')\) with message space \(\mathcal {M}'\) and fake encryption algorithm \(\overline{\mathsf {Enc}'}\). Output scheme: \((\mathsf {Keygen_{FO}},\mathsf {Encaps},\mathsf {Decaps})\) with key space \(\mathcal {K}\). (The key space is the space of encapsulated keys, not of public/secret key pairs.) \(\mathsf {PRF}\) is a pseudorandom function with key space \(\mathcal {K}_\mathsf {PRF}\). \(H:\mathcal {M}'\rightarrow \mathcal {K}\) is a hash function (modeled as a random oracle).
Security of Transformation \(\mathsf {U}^{\not \bot }_m\). HKSU does not show the security of transformation \(\mathsf {U}^{\not \bot }_m\) (in the sense of showing that \(\mathsf {Encaps}\) is secure if \(\mathsf {Enc}'\) satisfies certain properties), but instead directly analyzes the result of applying both \(\mathsf {T}\) and \(\mathsf {U}^{\not \bot }_m\). That is, they show that \(\mathsf {Encaps}\) is secure if \(\mathsf {Enc}\) satisfies certain properties. HKSU does not completely modularize the proof (i.e., it does not separately analyze \(\mathsf {T}\) and \(\mathsf {U}^{\not \bot }_m\)) but shows the following:
Theorem 2
Assume \(\mathsf {Enc}\) has injective encryptionFootnote 5 and is IND-CPA secure and DS secure and \(\varepsilon \)-disjoint, and has \(\varepsilon '\)-correctness.Footnote 6 (For negligible \(\varepsilon ,\varepsilon '\)) Then \(\mathsf {Encaps}\) (as constructed by transformations \(\mathsf {T}\) and \(\mathsf {U}^{\not \bot }_m\) from \(\mathsf {Enc}\)) is IND-CCA secure.
The result stated in HKSU includes concrete security bounds. We also recall the definition of IND-CCA security for KEMs used in the preceding theorem:
Definition 2
A KEM \((\mathsf {Keygen_{FO}},\mathsf {Encaps},\mathsf {Decaps})\) with key space \(\mathcal {K}\) is IND-CCA secure iff for any quantum-polynomial-time adversary A,  is negligible, using the games from Fig. 5.
is negligible, using the games from Fig. 5.
Intuitively, this means that A cannot distinguish between the true key \(K^*\) contained in the ciphertext \(c^*\) and a uniformly random key \(K^*\).
Note that in this definition, we slightly deviate from HKSU: In HKSU, only one game is given. This game picks randomly whether to play  or
or  from our definition. The security definition then requires that the adversary guesses which game is played with probability negligibly close to \(\frac{1}{2}\). (We call this a “bit-guessing-style definition”) In contrast, our definition requires the adversary to distinguish with its output bit between two games. (We call this a “distinguishing-style definition”.) It is well-known that bit-guessing-style and distinguishing-style definitions are equivalent. But in the context of formal verification, it seems (according to our experiences) easier to work with distinguishing-style definitions.
from our definition. The security definition then requires that the adversary guesses which game is played with probability negligibly close to \(\frac{1}{2}\). (We call this a “bit-guessing-style definition”) In contrast, our definition requires the adversary to distinguish with its output bit between two games. (We call this a “distinguishing-style definition”.) It is well-known that bit-guessing-style and distinguishing-style definitions are equivalent. But in the context of formal verification, it seems (according to our experiences) easier to work with distinguishing-style definitions.
Security Proof of Transformation \(\mathsf {U}^{\not \bot }_m\). We give a compressed overview of the proof of Theorem 2 from HKSU. For details, see [16].
Fix an adversary A. By definition of IND-CCA security (Definition 2), we need to bound  for the games from Fig. 5.
for the games from Fig. 5.
We use essentially the same games in this proof as HKSU, with one difference: Since we decided to define IND-CCA security via a distinguishing-style definition, we need to adapt the games accordingly. All arguments from HKSU carry over trivially to our changed presentation.
The first step is to rewrite  by unfolding the definitions of \(\mathsf {Keygen_{FO}}\), \(\mathsf {Encaps}\), \(\mathsf {Decaps}\). (I.e., we make all constructions introduced by \(\mathsf {T}\) and \(\mathsf {U}^{\not \bot }_m\) explicit.) In addition, we replace the PRF by a uniformly random function \(H_r\) (that is not accessible to the adversary). The resulting game is:
by unfolding the definitions of \(\mathsf {Keygen_{FO}}\), \(\mathsf {Encaps}\), \(\mathsf {Decaps}\). (I.e., we make all constructions introduced by \(\mathsf {T}\) and \(\mathsf {U}^{\not \bot }_m\) explicit.) In addition, we replace the PRF by a uniformly random function \(H_r\) (that is not accessible to the adversary). The resulting game is:

Here \((A\rightarrow B)\) is the set of functions from A to B. And \(\mathcal {C}\) is the ciphertext space.
From the fact that \(\mathsf {PRF}\) is a pseudorandom function, we get that  is negligible.
is negligible.
Next, we chose the random oracle H differently: Instead of chosing H uniformly, we define it as the composition of a uniformly random function \(H_q\) and the encryption function  . (The \(\mathord -\) stands for the function argument.) Since \(\mathsf {Enc}\) has injective encryption, \(\mathsf {Enc}( pk ,\mathord -;G(\mathord -))\) is injective, and thus H is still uniformly distributed. We get the following game (changed lines are marked with boldface line numbers):
. (The \(\mathord -\) stands for the function argument.) Since \(\mathsf {Enc}\) has injective encryption, \(\mathsf {Enc}( pk ,\mathord -;G(\mathord -))\) is injective, and thus H is still uniformly distributed. We get the following game (changed lines are marked with boldface line numbers):

Note that we additionally replaced two invocations \(H(m^*)\), H(m) by \(H_q(c^*)\), \(H_q(c)\). By construction, the new invocations return the same values. We have \(\Pr [b=1:\text {Game 0}] = \Pr [b=1:\text {Game 1}]\).
In the next game hop, we change the decapsulation oracle. Instead of returning \(H_r(c)\) or \(H_q(c)\), depending on the result of the decryption, we now always return \(H_q(c)\). The resulting game is:

Since \(H_r\) and \(H_q\) are both random functions, at the first glance it might seem that this change does not matter at all, the return value is still random. However, \(H_q\) is indirectly accessible to the adversary via H! A more careful case analysis reveals that the adversary can distinguish the two games if it finds a message m with “bad randomness”. That is, a message m such that \(\mathsf {Dec}( sk ,\mathsf {Enc}( pk ,m; r))\ne m\) where \(r := G(m)\). If such bad randomness did not exist (i.e., when using a perfectly correct base scheme), this case would never happen. However, we do not assume perfect correctness. The solution from HKSU is to first replace the uniformly chosen \(G\overset{\$}{\leftarrow }(\mathcal {M}\rightarrow \mathcal {R})\) by a G that outputs only good randomness (short: a “good G”). I.e., for each m, \(G(m):=r\) is chosen uniformly from the set of all r with \(\mathsf {Dec}( sk ,\mathsf {Enc}( pk ,m;r))=m\). Once we have such a good G, bad randomness does not occur any more, and we can show that switching between \(H_r\) and \(H_q\) cannot be noticed (zero distinguishing probability). And then we replace G back by \(G\overset{\$}{\leftarrow }(\mathcal {M}\rightarrow \mathcal {R})\).
To show that replacing the uniform G by a good G, HKSU reduces distinguishing the two situations to distinguishing a sparse binary function F from a constant-zero function \(F_0\) (given as an oracle). And for that distinguishing problem (called GDPB), they give a lemma that shows the impossibility of distinguishing the F and \(F_0\). Altogether, we get that \(|{\Pr [b=1:\text {Game 1}]-\Pr [b=1:\text {Game 2}]}|\) is negligible.
Our formalization deviates somewhat from that proof: Instead of using the lemma about GDPB (which we would have to implement in the tool, first), we use the O2H Theorem [1] to show this indistinguishability. (We had to implement the O2H Theorem anyway because it is used in the analysis of transformation \(\mathsf {T}\).)
Note that this makes our bound somewhat worse. In HKSU, the proof step involving GDPB leads to a summand of \(O(q^2\delta )\) in the final bound, while we achieve \(O(q\sqrt{\delta })\) instead (last but one summand of (1)). Here q is the number of queries and \(\delta \) the correctness error of the underlying scheme.
In the next game, we change how the challenge ciphertext \(c^*\) is generated. Instead of encrypting \(m^*\), we simply produce a fake ciphertext \(c^* \leftarrow \overline{\mathsf {Enc}}( pk )\). The resulting game is:

By DS security of \(\mathsf {Enc}\), this fake encryption cannot be distinguished from a real encryption. (Note that the secret key is not used any more in Game 2.) Hence \(|{\Pr [b=1:\text {Game 2}]-\Pr [b=1:\text {Game 3}]}|\) is negligible.
Finally, we change how \(K^*\) is chosen. Instead of picking \(K^*:=H_q(c^*)\), we chose \(K^*\) uniformly:

Since \(H_q\) is a random function, this change can only be noticed if \(H_q(c^*)\) is queried somewhere else. The adversary has access to \(H_q\) via H, but through H it can only query \(H_q\) on values that are in the range of \(\mathsf {Enc}\). But since \(c^*\) was constructed as a fake encryption \(\overline{\mathsf {Enc}}( pk )\), the \(\varepsilon \)-disjointness of \(\overline{\mathsf {Enc}}\) guarantees that \(c^*\) is, with overwhelming probability, not in the range of \(\mathsf {Enc}\). In that case, \(H_q(c^*)\) is independent from anything the adversary might query. Thus \(|{\Pr [b=1:\text {Game 3}]-\Pr [b=1:\text {Game 4}]}|\) is negligible.
So far, we have shown that the games  and Game 4 are indistinguishable. To show indistinguishability of
and Game 4 are indistinguishable. To show indistinguishability of  and
and  , we write down a similar sequence of games Game 0’ to Game 4’ where \(K^*\) is chosen uniformly (as in
, we write down a similar sequence of games Game 0’ to Game 4’ where \(K^*\) is chosen uniformly (as in  ). We then have indistinguishability of
). We then have indistinguishability of  and Game 4’. Game 4 and Game 4’ are identical, thus
and Game 4’. Game 4 and Game 4’ are identical, thus  and
and  are indistinguishable, finishing the proof of IND-CCA security of \(\mathsf {Encaps}\).
are indistinguishable, finishing the proof of IND-CCA security of \(\mathsf {Encaps}\).
4 Formalizing HKSU – the Specification
A proof (formal or pen-and-paper) will consist of two separate parts: A specification of the result that is proven, and the proof itself. This separation is important because if we trust that the proof is correct, we only need to read the specification. In a pen-and-paper proof, this specification will usually consist of the theorem together with all information required for interpreting the theorem, i.e., all definitions that the theorem refers to, and all assumptions (if they are not stated within the theorem itself). In the case of formal verification, we tend to trust the proof (because it has been verified by the computer) but we have to check the specification – does it indeed encode what we intended to prove?
In this section we go through the specification part of our HKSU formalization (available at [33]). It consists roughly of five parts: The main theorem. The specification of the encryption algorithm and other functions in Isabelle/HOL. The specification of the security definitions (security games). The specification of the adversary. And the specification of the reduction-adversaries (we explain below why this is a relevant part of the specification).
The Main Theorem. The source code for the main theorem is shown in Fig. 6. Line 2 is the IND-CCA advantage \(\mathsf {Adv_{CCA}}\) of the adversary attacking the KEM \(\mathsf {Encaps}\) resulting from the transformations \(\mathsf {Punc}\), \(\mathsf {T}\), \(\mathsf {U}^{\not \bot }_m\). (See Sect. 3.3.) \(\mathsf {Adv_{CCA}}\) is defined as the difference between the probability of adversary-output \(b=1\) in games indcca_encFO_0 and indcca_encFO_1. We will see those games below. In 4 we have the advantage \(\mathsf {Adv_{PRF}}\) of a reduction-adversaryFootnote 7 against the pseudorandom function \(\mathsf {PRF}\), expressed as the probability-difference between games PRF_real and PRF_ideal. In 5, we have basically the same but with respect to a different reduction-adversary. We have two reduction-adversaries for \(\mathsf {PRF}\) since we used the pseudorandomness twice in the proof. Since the adversary is hardcoded in the games,Footnote 8 we express this in terms of further games PRF_real’ and PRF_ideal’. In 6 we have the IND-CPA advantage \(\mathsf {Adv_{CPA}'''}\) of a reduction-adversary against the base scheme \(\mathsf {Enc}_0\), expressed in terms of games indcpa_enc0_0’’’ and indcpa_enc0_1’’’. Similarly, we have advantages \(\mathsf {Adv_{CPA}''}\) in lines 7–8, \(\mathsf {Adv_{CPA}'}\) in 6, and \(\mathsf {Adv_{CPA}}\) in lines 7–8, against further reduction-adversaries. The term \(\delta :=\texttt {correctness params0 ...}\) in lines 11 and 12 refers to the correctness of \(\mathsf {Enc}_0\), i.e., we assume \(\mathsf {Enc}_0\) to be \(\delta \)-correct. (Cf. Footnote 6 for the meaning and Fig. 7 for the formalization of correctness.) Finally, card (msg_space()) is the cardinality of the message space \(\mathcal {M}\) of \(\mathsf {Enc}\). \(q_G,q_H,q_D\) are the number of queries made to the three oracles, and \(q:=q_G+2q_H\). With the notation we introduced in this explanation, we can write the main theorem more readably:
Encryption Algorithm and Other Definitions. In order to make sense of the main theorem, we first need to check the definitions of the KEM and the building blocks used in its construction. The simplest is the pseudorandom function \(\mathsf {PRF}\), defined in Fig. 8, lines 1–2. The axiomatization command declares two constants PRF (the PRF) and keygenPRF (the key generation algorithm for the PRF, given as a distribution over keys). It furthermore axiomatizes the fact the key generation is a total distribution (axiom keygenPRF_total). (We do not need to axiomatize the security of PRF; its security is used implicitly by having \(\mathsf {Adv_{PRF}}\) occur in the main theorem.)
Similarly, we axiomatize the encryption scheme \(\mathsf {Enc}_0\) in lines 4–16. All encryption schemes in our work consist of a public parameter distribution (we only use this here for chosing the random oracles), a key generation, an encryption, a decryption algorithm, and a message space (which we allow to depend on the public parameters). The base scheme does not have public parameters, so we define params0 as the point distribution that always returns the dummy value () (4). The key generation keygen0 (lines 6–9) takes the public parameter and returns a distribution of public/secret key pairs. We assume that key generation is a total distribution (axiom weight_keygen0). Additionally we assume a function pk_of_sk that returns the corresponding pk for every sk in the support of keygen.Footnote 9 We define the encryption by first defining enc0r, a function that takes the public parameters, public key, message, and explicit randomness to compute a ciphertext (11). From this we define enc0 as the distribution resulting from applying enc0r to the uniform distribution on the randomness (12). Decryption (dec0, 13) may fail, hence the return type is msg option, which means it can be None or Some m with a message m. Finally, msg_space0 is a non-empty set (lines 15–16). We have an additional axiom enc0_injective (lines 18–19) which encodes the assumption that our base scheme is injective. (Cf. Footnote 5 for the meaning and Fig. 7 for the formalization of injective_enc.)
The transformations \(\mathsf {Punc}\), \(\mathsf {T}\), and \(\mathsf {U}^{\not \bot }_m\) are given in Fig. 9. As with our base scheme, we always define a deterministic encryption/encapsulation that takes explicit randomness first. The final KEM consists of the functions keygenFO, encapsFO, decapsFO, etc. We omit a discussion of the details of the function definitions, they follow our exposition in Sect. 3.
Security Definitions/Games. Next we have to understand the games that define the various advantages in the main theorem. We start with the IND-CCA security of \(\mathsf {Encaps}\). \(\mathsf {Adv_{CCA}}\) was defined as the difference in probabilities that an adversary A (Adv_INDCCA_encFO in our case) outputs \(b=1\) in games indcca_encFO_0/1. The formalization of these games is given in Fig. 10. It is a direct encoding of the games in Fig. 5, with several small differences: Since we do not support procedures with parameters and return values, we use the global variables in_pk and in_cstar and Kstar for the inputs \( pk \) and \(c^*\) and \(K^*\). And the global variable b is used for the return value (guessing bit). Below, when defining the adversary, we will then make sure the adversary gets access to those global variables.Footnote 10 Access to the oracle decapsQuery is by passing it to the adversary as one of the oracles. Communication with decapsQuery is through variables c (input) and K’ (output). It checks explicitly whether \(c\ne c^*\) and returns None otherwise. (In Fig. 5, it was not made explicit how we enforce \(c\ne c^*\).) Additionally, we model the access to the random oracles G, H by giving A access to queryG, queryH. queryG operates on global variables Gin, Gout and applies the unitary transformation Uoracle G on them. (Uoracle is a built-in function that transforms a function G into a unitary \(|{x,y}\rangle \mapsto |{x,y\oplus G(x)}\rangle \).) Analogously queryH.
Similarly we define the games used in the rhs (right hand side) of the main theorem. The games PRF_real and PRF_ideal defining PRF-security for adversary Adv_PRF are given in Fig. 11. Again, we define oracles to either evaluate a pseudo-random function PRF or a random function RF and pass them to the adversary. The adversary Adv_PRF is explicitly defined in terms of Adv_INDCCA_encFO as part of our reduction, but its implementation details do not matter for us (except for some necessary sanity checks, see below). The primed variants Adv_real’ and Adv_ideal’ are identical except that they use a different reduction-adversary.
Similarly, we define IND-CPA security of \(\mathsf {Enc}_0\) against Adv_INDCPA_enc0_1/2 in Fig. 12. The primed variants are identical except that they use a different adversary.
The Adversary. In the games indcca_encFO_1/2, we use the adversary \(A:={}\)Adv_INDCCA_encFO. Since we want the main theorem to hold for arbitrary adversaries, we need to declare the adversary as an unspecified program. This is done in Fig. 13. It declares that the adversary has access to the variables classA, quantA, b, in_pk, in_cstar, Kstar, i.e., we say the adversary has those free variables. Here classA, quantA are the global state of the adversary (quantum and classical part), and the others are the variables used for inputs/outputs of the adversary. Furthermore, the adversary needs to be able to access the variables Hin, Hout, Gin, Gout, c, K’ that are used as inputs/outputs for its oracles decapsQuery, queryG, queryH (see above). Those variables are not declared as free variables (i.e., the adversary will have to hide them under a local command) but may be used internally, in particular before or after invoking the oracle. Finally, calls ?,?,? means that the adversary takes three oracles.
However, we are not interested in arbitrary adversaries, but in ones that always terminate and that make \(\le q_G,q_H,q_D\) queries to its various oracles. For this, we add various axioms to the file axioms.qrhl, stating the termination and the number of queries performed when instantiated with various oracles. The file with all axioms is discussed in the full version [35]. Unfortunately, this file contains a lot of repetitions because qrhl-tool does not allow us to allquantify over the oracles, so we need to state the axioms for any oracle we want to instantiate the adversary with.Footnote 11
Reduction-Adversaries. Finally, to fully check whether the main theorem states what we want it to state (namely, that the KEM \(\mathsf {Encaps}\) is secure assuming that the underlying encryption scheme \(\mathsf {Enc}_0\) and the PRF are secure), we also need to inspect the reduction-adversaries. This is because the main theorem basically says: If Adv_INDCCA_encFO breaks \(\mathsf {Encaps}\), then one of the adversaries in the games on the rhs breaks \(\mathsf {Enc}_0\) or \(\mathsf {PRF}\). (I.e., one of Adv_PRF, Adv_PRF’, Adv_INDCPA_enc0/1, etc.) But this is vacuously true – it is easy to construct an adversary that breaks \(\mathsf {Enc}_0\) or \(\mathsf {PRF}\). Namely, that adversary could run in exponential-time and perform a brute-force attack. Or that adversary could directly access the global variables containing, e.g., the secret key. So, while the exact details of what the reduction-adversaries do are not important, we need to check: Are the reduction-adversaries quantum-polynomial-time if Adv_INDCCA_encFO is? (Or even some more refined runtime relationship if we want tight concrete security bounds.) And do the reduction-adversaries access only variables that are not used by the security games themselves? The latter can be checked using the print command in interactive mode that prints all variables of a program (e.g., print Adv_PRF). This shows that the adversaries in the PRF games only access cstar, classA, b, c, K’, quantA, and in particular not prfk or RF. And the adversaries in the IND-CPA games access only Find, mstar, S, in_cstar, in_pk, classA, b, is_puncture, G, quantA, but not the forbidden sk, pk, cstar.Footnote 12 To check the runtime of the adversaries, there is currently no better way than to manually inspect the code of all adversaries explicitly to see whether they do anything that increases the runtime too much. To the best of our knowledge, this is the state-of-the-art also in classical crypto verification. We believe that coming up with formal verification support for runtime analysis in qrhl-tool and similar tools is a very important next step. If this would be solved, the reduction-adversaries could be removed from the list of things we need to check as part of the specification.
By checking all the above points, we can have confidence that the formal proof indeed proves the right thing. (There are quite a lot of points to check, but we stress that in a pen-and-paper proof, the situation is similar – one needs to check whether all security definitions are correct, etc.)
5 Formalizing HKSU – The Proof
Since the formal proof is much too long to go through in detail, we only show a few select elements here to given an impression. HKSU shows security of three transformations \(\mathsf {Punc}\), \(\mathsf {T}\), \(\mathsf {U}^{\not \bot }_m\). The proof follows the overall structure of HKSU, lemma_ds_security.qrhl and lemma_indcpa_security.qrhl establishing DS and IND-CPA security of \(\mathsf {Punc}\), lemma_ds_encT_security.qrhl establishing DS security of \(\mathsf {T}\), and lemma_encFO_indcca.qrhl establishing IND-CCA security of the combination of \(\mathsf {T}\) and \(\mathsf {U}^{\not \bot }_m\). Finally lemma_security_encFO.qrhl combines all those results into one overall result, the “main theorem” discussed in Sect. 4.
lemma_encFO_indcca.qrhl establishes IND-CCA security using the same sequence of games as described in Sect. 3.3, encoded as programs game0FO, ..., game4FO, game3FO’, ..., game0FO’ in the eponymous files.
Game 1 to Game 2. We zoom in some more onto the proof of the relationship between Game 1 and Game 2 (lemma_game1FO_game2FO.qrhl). We follow the basic intuition from Sect. 3.3, and split the proof of that step into the following subgames (all in eponymous .qrhl files):
-
(1)
game1FO: Game 1 from Sect. 3.3.
-
(2)
game1FO_goodbad: In this game, we prepare for replacing uniform G by a good G. For this purpose, instead of picking G uniformly, we pick a good Ggood (i.e., picking \(\texttt {Ggood}(m)\) uniformly from the good randomnesses for every m) and a bad Gbad, and a set S of messages. We define G(m) to be \(\texttt {Ggood}(m)\) if \(m\notin \mathtt {S}\) and \(\texttt {Gbad}(m)\) otherwise. By choosing the distribution of S properly, we have that the resulting G is still uniform.
We additionally remove all direct access to G, and make sure that queryG is used everywhere instead. This is necessary for bringing the game into the shape needed in the following step. This means all classical queries to G (e.g., in the creation of the challenge ciphertext) need to be replaced by quantum queries with subsequent measurements (we define a wrapper oracle ClassicalQueryG(queryG) for this), and we cannot simply define the function H in terms of G (see Game 1, line 03 in Sect. 3.3). Instead, we need to construct an oracle queryH_Hq that implements superposition queries of H in terms of superposition queries of G (via queryG). This makes this proof step considerably more complex than many of the other game steps. That \(\Pr [b=1]\) does not change is shown in lemma_game1FO_goodbad.qrhl.
-
(3)
game1FO_goodbad_o2h_right: We rewrite the previous game to have the right shape for the O2H theorem. The O2H theorem allows us to replace one oracle by another one that differs only in a few (hard to find) places. In order to apply the O2H theorem [1] (or the o2h tactic in qrhl-tool), the game needs to have a very specific form:
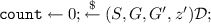
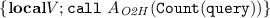 for an oracle Count that counts queries in variable count and query that implements superposition queries to \(G'\). The distribution \(\mathcal {D}\) and the program \(A_ O2H \) can be chosen freely. In our case we choose \(\mathcal {D}:=\texttt {goodbad\_o2h\_distr}\) such that \(G'\) is G from the previous game, and G is Ggood, and we choose \(A_ O2H =\texttt {Adv\_O2H\_Game1FO}\) to simulate the rest of the game. We show that the probability of \(\Pr [b=1]\) does not change (lemma_game1FO_goodbad_o2h_right.qrhl).
for an oracle Count that counts queries in variable count and query that implements superposition queries to \(G'\). The distribution \(\mathcal {D}\) and the program \(A_ O2H \) can be chosen freely. In our case we choose \(\mathcal {D}:=\texttt {goodbad\_o2h\_distr}\) such that \(G'\) is G from the previous game, and G is Ggood, and we choose \(A_ O2H =\texttt {Adv\_O2H\_Game1FO}\) to simulate the rest of the game. We show that the probability of \(\Pr [b=1]\) does not change (lemma_game1FO_goodbad_o2h_right.qrhl). -
(4)
game1FO_goodbad_o2h_left: We replace queries to \(G'\) by queries to G (recall that G was, in the previous game, made to return only good randomness). The Semiclassical O2H theorem [1] (implemented via our tactic o2h) allows us to do this replacement. In the resulting game \(\Pr [b=1]\) will differ by an amount that can be bounded in terms of the probability of finding an element in S. Bounding this probability involves a side-chain of games that we omit here. Altogether, lemma_game1FO_o2h_concrete.qrhl gives a concrete bound on the difference of \(\Pr [b=1]\).
-
(5)
game1FO_goodbad_o2h_left’: We remove the query-counting wrapper oracle Count that was introduced for the o2h tactic. We do this in a separate game step because it would be in the way in the next step. The probability \(\Pr [b=1]\) does not change (lemma_game1FO_goodbad_o2h_left’.qrhl).
-
(6)
game1FO_goodbad_o2h_left_class: We unwrap the adversary Adv_O2H_Game1FO again which we introduced in (). We also undo the various replacements done in (2) (which ensured that G was never used directly) to make the game simpler for the following steps. The probability \(\Pr [b=1]\) does not change (lemma_game1FO_goodbad_o2h_left_class.qrhl).
-
(7)
game1FO_goodbad_badpk: In (2), we ignored one problem: Even if there is just one m without any good randomness, then it is not well-defined to pick G uniformly from the set of good G’s because that set is empty.Footnote 13 For that reason, in (2), we actually defined G(m) to be good if good randomness exists. But this definition breaks the next step below which relies on the fact that all randomness is good. Our solution is to introduce a predicate bad_pk pk sk that tells us whether there is an m (for that key pair) without good randomness. We then change the definition of the game to make a case distinction on bad_pk pk sk. If true, the new game behaves in a way that makes the next proof step trivially true. If false, the new game behaves as before. The probability for bad_pk pk sk is bounded by the correctness error of \(\mathsf {Enc}_0\), so we can bound the difference of \(\Pr [b=1]\) in lemma_game1FO_goodbad_badpk.qrhl.
-
(8)
game2FO_goodbad_range: In the previous games, the choice whether \({Decaps}\) returns \(H_r(c)\) or \(H_q(c)\) depended on whether we have a reencryption failure or not. (See \({Decaps}\) in Game 1 in Sect. 3.3.) Instead, we use \(H_r(c)\) or \(H_q(c)\) depending on whether c is in the range of \(\mathsf {Enc}'\). We can show that, assuming good randomness, these two conditions are equivalent. Since G contains only good randomness, \(\Pr [b=1]\) does not change (lemma_game1FO_game2FO_o2h.qrhl).
-
(9)
game2FO_goodbad_o2h_left’: In the previous game, \(\mathsf {Decaps}\) returns \(H_r(c)\) if c is not in the range of \(\mathsf {Enc}'\). We replace this by always returning \(H_q(c)\) as in Game 2 (Sect. 3.3). By analysis of the game, we can see that \(H_q\) is used in other places of the game only on the range of \(\mathsf {Enc}'=\mathtt {encT}\), hence \(H_q(c)\) and \(H_r(c)\) are both fresh randomness if c is not in the range. Hence the replacement does not change \(\Pr [b=1]\) (lemma_game2FO_goodbad_range.qrhl).
-
(10)
The rest of the proof steps are analogous to those done in (2)–(6), in reverse order until we reach game2FO.
Verification of ClassicalQueryG. To finish our illustration, we give the details of one of the subproofs of step (2), namely the proof that accessing G directly is the same querying G via ClassicalQueryG(queryG). The source of ClassicalQueryG is given in Fig. 14, lines 1–6. It initializes Gin with \(|{\mathtt {gin}}\rangle \), Gout with \(|{\mathtt {gout}}\rangle \), calls the query oracle (which will query G in superposition), and measures Gout into gout. Lines 8–11 claim that after doing so (in the right program) we will have gout2 = G2(gin2). And furthermore, that this preserves quantum equality of quantA, aux between the left and right side. Lines 13–14 inlines the definitions of the programs that we use, and lines 15–16 removes the local variable declarations. (The subgoal now has the same pre-/postcondition as before, but the right program is the code of ClassicalQueryG without the local statement.) Then wp right (17) consumes the statement  , and the postcondition becomes (after simplification) what is written in lines 18–19. Basically, this proof step tells us that having \(|{\mathtt {gin2},\mathtt {G2\ gin2}}\rangle \) in Gin2,Gout2 is sufficient for having gout2 = G2(gin2) after measurement. Next (lines 21–24) we consume “on Gin,Gout apply (Uoracle G)” from queryG (see Fig. 10, evaluation of G in superposition) and show that now it is sufficient to have \(|{\mathtt {gin2},0}\rangle \) in Gin2,Gout2. In lines 25–29, we remove the initialization
, and the postcondition becomes (after simplification) what is written in lines 18–19. Basically, this proof step tells us that having \(|{\mathtt {gin2},\mathtt {G2\ gin2}}\rangle \) in Gin2,Gout2 is sufficient for having gout2 = G2(gin2) after measurement. Next (lines 21–24) we consume “on Gin,Gout apply (Uoracle G)” from queryG (see Fig. 10, evaluation of G in superposition) and show that now it is sufficient to have \(|{\mathtt {gin2},0}\rangle \) in Gin2,Gout2. In lines 25–29, we remove the initialization  , now the necessary condition is to have \(|{\mathtt {gin}}\rangle \) in Gin2. And in lines 30–32, we remove
, now the necessary condition is to have \(|{\mathtt {gin}}\rangle \) in Gin2. And in lines 30–32, we remove  , removing the last requirement. Now left and right program are both skip and the pre-/postcondition are identical. The skip tactic (33) solves such a qRHL subgoal.
, removing the last requirement. Now left and right program are both skip and the pre-/postcondition are identical. The skip tactic (33) solves such a qRHL subgoal.
6 Conclusion
In this work, we have shown how to formally verify the HKSU security proof of a Fujisaki-Okamoto variant.
The experience shows that formal proofs of post-quantum secure schemes seem definitely possible using the approach in the qrhl-tool. Besides challenges due to the early development stage of the tool, probably the most troublesome part is reasoning about quantum computations. E.g., in one technical lemmaFootnote 14 we show that a superposition query to the function \(H:=H_q(\mathsf {Enc}( pk ,\mathord -;G(\mathord -)))\) as defined in Game 1, line 03 in Sect. 3.3 can be implemented by the simply quantum circuit that performs a superposition query to G, a superposition query to \(H_q(\mathsf {Enc}( pk ,\mathord -;\mathord -))\) and another superposition query to G for uncomputation.Footnote 15 The simplification of the resulting verification condition is a 200 lines Isabelle proof that takes almost ten minutes to execute (on the authors laptop).Footnote 16 Given the simplicity of the fact that is proven, we feels this proof should be fully automatic and finish almost instantaneously.
What other post-quantum security proofs are possible using the same methodology? We feel that proofs of other post-quantum secure cryptographic schemes both in the standard model and the random oracle model should be feasible as well, as long as they do not use any advanced random oracle reasoning techniques beyond the O2H Theorem. How hard or easy it is to handle other proof techniques for the random oracle, or proof techniques that involve rewinding (which is notoriously challenging in the quantum setting) is not clear at this point. Similarly, it is not clear at this point how easily security proofs that involve reasoning about quantum information theory (such as quantum key distribution proofs, for example) can be formalized.
Possible directions for future research include:
-
Formalizations of security proofs of the actual NIST candidates. While HKSU is quite close to some of the NIST candidates, to have highest assurance, we should analyze the schemes exactly as standardized and not merely schemes that are very similar to them. While unlikely, even a small difference such as the order in which the different inputs to a hash functions are concatenated might make a scheme insecure.
-
Improved methods for reasoning about the quantum parts of the schemes, in particular methods for evaluating quantum computations such as the one mentioned in the beginning of this section. (Sequences of applications of unitaries in the program translate to multiplications of operators in the pre-/postconditions.)
-
Support for other post-quantum security proof techniques beside the O2H Theorem. (E.g., rewinding, other random-oracle proof techniques.) Ideally, those proof techniques should be derived in the tool directly from first principles.
-
Formal verification of “fully quantum” protocols such as quantum key distribution, quantum money, etc.
Notes
- 1.
A KEM, key encapsulation scheme, is similar to an encryption scheme but specialized for use in hybrid encryption schemes.
- 2.
To be precise, we formalize the security proof from the February 2019 version [16] of [17]. The proof has been improved upon in later revisions of the paper. In particular, the requirement of injective encryption (see Footnote 5) has been removed. We formalized the earlier version of the proof since the formalization was already under way when the proof was updated. Their new proof does not use substantially different techniques, and we believe that formalizing their new proof in qRHL would not pose any challenges different from the ones encountered in this work. However, since their new proof is an almost complete rewrite (i.e., a different proof), it is not possible to simply update our formalization. Instead, a new development from scratch would be needed.
- 3.
Semantically, call X is not a separate language feature. It just means that the source code of X is included verbatim at this point.
- 4.
Note that HKSU [16] instead uses a secret random function \(\mathsf H_r\). (Not a public random function like the random oracle.) But it is understood that this secret random function is to be implemented by a PRF. Here, we directly use the PRF since we want to avoid keeping the proof step that replaces the PRF by a random function implicit.
- 5.
This means that for any \(m_0\ne m_1\) in the message space, \(\mathsf {Enc}( pk ,m_0)\ne \mathsf {Enc}( pk ,m_1)\) with probability 1. Note that this does not imply the possibility of correct decryption: While information theoretically, the plaintext is determined by the ciphertext, it may be computationally infeasible to determine the correct plaintext with probability 1, even given the secret key.
- 6.
This means that for random \(( pk , sk )\leftarrow \mathsf {Keygen}()\) and worst-case m, \(\mathsf {Dec}( sk ,\mathsf {Enc}( pk ,m))=m\) with probability at least \(1-\varepsilon \). See [16] for a precise definition.
- 7.
By reduction-adversary, we mean an adversary that we have explicitly constructed.
- 8.
Due to a lack of a proper module system in qrhl-tool, we have a lot of code duplication. A module system for games and adversaries such as in EasyCrypt would be a valuable addition to qrhl-tool and would have simplified our proofs considerably.
- 9.
This assumption is not explicit in HKSU but clearly necessary for defining the decryption in transformation \(\mathsf {T}\): since the decryption re-encrypts, it needs to know the public key.
- 10.
We do not use pk and cstar directly for passing \( pk \) and \(c^*\) since that would mean giving A access to those variables. Then A could change the value of \( pk \) and \(c^*\) but the oracle decapsQuery relies on having the original values of \( pk \) and \(c^*\).
- 11.
Another place where a more advanced module system would help, cf. Footnote 8.
- 12.
Again, a more refined module system would allow us to automatically derive that certain variable-disjointness conditions hold, cf. Footnote 8.
- 13.
This problem also exists in HKSU but was not noticed there.
- 14.
File lemma_queryH_invariant.qrhl.
- 15.
This quantum circuit is formalized as a program in file queryH_Hq.qrhl.
- 16.
File FO_Proofs_Very_Slow.thy.
References
Ambainis, A., Hamburg, M., Unruh, D.: Quantum security proofs using semi-classical oracles. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11693, pp. 269–295. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_10
Arute, F., et al.: Quantum supremacy using a programmable superconducting processor. Nature 574(7779), 505–510 (2019)
Barthe, G., Grégoire, B., Heraud, S., Béguelin, S.Z.: Computer-aided security proofs for the working cryptographer. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 71–90. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_5
Barthe, G., Grégoire, B., Lakhnech, Y., Zanella Béguelin, S.: Beyond provable security verifiable IND-CCA security of OAEP. In: Kiayias, A. (ed.) CT-RSA 2011. LNCS, vol. 6558, pp. 180–196. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19074-2_13
Barthe, G., Grégoire, B., Zanella Béguelin, S.: Formal certification of code-based cryptographic proofs. In: POPL, pp. 90–101. ACM (2009)
Bellare, M., Rogaway, P.: Random oracles are practical: A paradigm for designing efficient protocols. In: CCS ’93, pp. 62–73. ACM (1993)
Bellare, M., Rogaway, P.: Optimal asymmetric encryption. In: De Santis A. (eds.) Advances in Cryptology – EUROCRYPT’94, Lecture Notes in Computer Science, vol. 950. Springer, Berlin, vol. 950, pp. 92–111. (1994) https://doi.org/10.1007/BFb0053428
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 409–426. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_25
Boneh, D., Dagdelen, Ö., Fischlin, M., Lehmann, A., Schaffner, C., Zhandry, M.: Random oracles in a quantum world. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 41–69. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_3
Bos, J., et al.: CRYSTALS - kyber: a CCA-secure module-lattice-based KEM. IACR ePrint 2017/634 (2017)
Canetti, R., Goldreich, O., Halevi, S.: The random oracle methodology, revisited. In: STOC 1998, pp. 209–218. ACM (1998)
Fujisaki, E., Okamoto, T.: How to enhance the security of public-key encryption at minimum cost. IEICE Trans. Fund. Electron. Commun. Comput. Sci. E83–A(1), 24–32 (2000)
Fujisaki, E., Okamoto, T., Pointcheval, D., Stern, J.: RSA-OAEP is secure under the RSA assumption. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 260–274. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_16
Fujisaki, E., Okamoto, T., Pointcheval, D., Stern, J.: RSA-OAEP is secure under the RSA assumption. J. Crypto 17(2), 81–104 (2004)
Hofheinz, D., Hövelmanns, K., Kiltz, E.: A modular analysis of the Fujisaki-Okamoto transformation. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 341–371. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_12
Hövelmanns, K., Kiltz, E., Schäge, S., Unruh, D.: Generic authenticated key exchange in the quantum random oracle model. IACR ePrint 2018/928, rev. February 14, 2019 (2019), preliminary version of [17]
Hövelmanns, K., Kiltz, E., Schäge, S., Unruh, D.: Generic authenticated key exchange in the quantum random oracle model. In: Kiayias, A., Kohlweiss, M., Wallden, P., Zikas, V. (eds.) PKC 2020. LNCS, vol. 12111, pp. 389–422. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45388-6_14
Inoue, A., Iwata, T., Minematsu, K., Poettering, B.: Cryptanalysis of OCB2: attacks on authenticity and confidentiality. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11692, pp. 3–31. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_1
ISO: Information technology - security techniques - authenticated encryption. International Standard ISO/IEC 19772 (2009)
Naehrig, M., et al.: Frodokem. Technical Report, National Institute of Standards and Technology (2017)
Nipkow, T.: Programming and proving in isabelle/hol. https://isabelle.in.tum.de/website-Isabelle2019/dist/Isabelle2019/doc/prog-prove.pdf (2019), version for Isabelle 2019
Nipkow, T., Wenzel, M., Paulson, L.C. (eds.): Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
NIST: Post-quantum crypto standardization - call for proposals. http://csrc.nist.gov/groups/ST/post-quantum-crypto/call-for-proposals-2016.html (2016)
Rogaway, P.: Efficient instantiations of tweakable blockciphers and refinements to modes OCB and PMAC. In: Lee, P.J. (ed.) ASIACRYPT 2004. LNCS, vol. 3329, pp. 16–31. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30539-2_2
Saito, T., Xagawa, K., Yamakawa, T.: Tightly-secure key-encapsulation mechanism in the quantum random oracle model. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 520–551. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_17
Shor, P.W.: Algorithms for quantum computation: discrete logarithms and factoring. In: FOCS 1994, pp. 124–134. IEEE (1994)
Shoup, V.: OAEP reconsidered. J. Crypto 15(4), 223–249 (2002)
Shoup, V.: Sequences of games: a tool for taming complexity in security proofs. Cryptology ePrint 2004/332 (2004)
Targhi, E.E., Unruh, D.: Post-quantum security of the Fujisaki-Okamoto and OAEP transforms. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 192–216. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_8
Unruh, D.: Quantum proofs of knowledge. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 135–152. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_10
Unruh, D.: dominique-unruh/qrhl-tool: Proof assistant for qRHL. GitHub, https://github.com/dominique-unruh/qrhl-tool (2017–2020), binaries of the correct version are at https://github.com/dominique-unruh/qrhl-tool/releases/tag/v0.5
Unruh, D.: Quantum relational Hoare logic. Proc. ACM Program. Lang. 3, 1–31 (2019)
Unruh, D.: GitHub, https://github.com/dominique-unruh/hksu-verification/tree/asiacrypt2020 (2020), source code of the proofs described here
Unruh, D.: Local variables and quantum relational hoare logic. arXiv:2007.14155 [cs.LO] (2020)
Unruh, D.: Post-quantum verification of Fujisaki-Okamoto. IACR ePrint 2020/962 (2020), full version of this paper
Watrous, J.: Zero-knowledge against quantum attacks. SIAM J. Comput. 39(1), 25–58 (2009)
Acknowledgments
We thanks Kathrin Hövelmanns for valuable discussions. This work was supported by the US Air Force AOARD grant “Verification of Quantum Cryptography” (FA2386-17-1-4022), by the ERC consolidator grant CerQuS, by the Estonian Research Council grant PRG946, and by the Estonian Centre of Exellence in IT (EXCITE) funded by ERDF.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Unruh, D. (2020). Post-Quantum Verification of Fujisaki-Okamoto. In: Moriai, S., Wang, H. (eds) Advances in Cryptology – ASIACRYPT 2020. ASIACRYPT 2020. Lecture Notes in Computer Science(), vol 12491. Springer, Cham. https://doi.org/10.1007/978-3-030-64837-4_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-64837-4_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64836-7
Online ISBN: 978-3-030-64837-4
eBook Packages: Computer ScienceComputer Science (R0)


















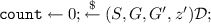
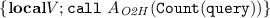 for an oracle
for an oracle 
