Abstract
Motivated by what we call “honest but lazy” parties in the context of secure multi party computation, we revisit the notion of multi-key FHE schemes (MFHE). In MFHE, any message encrypted using a public key \(pk_i\) can be “expanded” so that the resulting ciphertext is encrypted with respect to a set of public keys \((pk_1,..,pk_n)\). Such expanded ciphertexts can be homomorphically evaluated with respect to any circuit to generate a ciphertext \(ct\). Then, this ciphertext \(ct\) can be partially decrypted using a secret key \(sk_i\) (corresponding to the public key \(pk_i\)) to produce a partial decryption \(p_i\). Finally, these partial decryptions \(\{p_{i}\}_{i\in [n]}\) can be combined to recover the output. However, this definition of MFHE works only for n-out-of-n access structures and, thus, each node in the system is a point of failure. In the context of “honest but lazy” parties, it is necessary to be able to decrypt even when only given a subset of partial decryptions (say t out of n). In order to solve this problem, we introduce a new notion of multi-key FHE designed to handle arbitrary access patterns that can reconstruct the output. We call it a threshold multi-key FHE scheme (TMFHE).
Our main contributions are the following:
-
We formally define and construct TMFHE for any access structure given by a monotone boolean formula, assuming LWE.
-
We construct the first simulation-extractable multi-string NIZK from polynomially hard LWE.
-
We use TMFHE and our multi-string NIZK to obtain the first round-optimal (three round) MPC protocol in the plain model with guaranteed output delivery secure against malicious adversaries or, more generally, mixed adversaries (which supports “honest but lazy” parties), assuming LWE.
-
Our MPC protocols simultaneously achieve security against the maximum number of corruptions under which guaranteed output delivery is achievable, depth-proportional communication complexity, and reusability.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Starting with the breakthrough work of Gentry [21], fully homomorphic encryption (FHE) has been extensively studied over a long sequence of works (see e.g. [6, 8, 9, 21, 22]). In an FHE scheme, given a public key \(pk\) and a ciphertext of a message m encrypted using this public key, a user can homomorphically evaluate this ciphertext with respect to any circuit \(C\) to generate a new ciphertext \(ct\) that is an encryption of \(C(m)\) without learning anything about the message. Then, the decryptor, using the secret key \(sk\) can decrypt this message to recover the output \(C(m)\). However, traditionally, FHE schemes are single-key in nature: that is, they can be used to perform arbitrary computation on data encrypted using the same public key.
In this work, we build a new multi-party generalization of FHE that we call Threshold Multi-Key FHE, which we build from the LWE assumption. We then use this new primitive to achieve efficient secure multi-party protocols (MPC) in a model that allows for some honest parties to be “lazy”, as we discuss below. Subsequent to our work, our Threshold Multi-Key FHE was used in [26], which explicitly extends our MPC model with honest but lazy parties to also allow lazy parties to return in future rounds and builds upon our MPC protocol to achieve their results. We believe both our notion of Threshold Multi-Key FHE and our MPC model and protocol will continue to find other applications, as well (see e.g. [13], for another subsequent result that builds upon ours). We now elaborate on our contributions.
Multi-key FHE. Lopez-Alt et al. [32] introduced the notion of multi-key fully homomorphic encryption. Informally, in a multi-key FHE scheme, any message encrypted using a public key \(pk_i\) can be “expanded” so that the resulting ciphertext is encrypted with respect to a set of public keys \((pk_1,..,pk_n)\). Such expanded ciphertexts can be homomorphically evaluated with respect to any circuit to generate a ciphertext \(ct\). Then, this ciphertext \(ct\) can be partially decrypted using a secret key \(sk_i\) (corresponding to the public key \(pk_i\)) to produce a partial decryption \(p_i\). Finally, these partial decryptions \(\{p_{i}\}_{i\in [n]}\) can be combined to recover the output. In addition to the semantic security of encryption, a multi-key FHE scheme also requires that given any expanded (and possibly evaluated) ciphertext \(ct\) encrypting a message m, any set of \((n-1)\) secret keys \(\{sk_i \}_{i\ne i^{*}}\) for any \(i^*\), and the message m, it is possible to statistically simulate the partial decryption \(p_{i^*}\). Multi-key FHE has been extensively studied [7, 14, 33, 34] and has proven particularly useful in the context of building round-efficient secure multiparty computation protocols for protocols achieving security with abort. Recall that in security with abort, a single party that aborts could potentially prevent all honest parties from receiving the output.
1.1 A New Primitive: Threshold Multi-key FHE
However, none of the existing multi-key FHE schemes enable the output to be reconstructed unless all the n partial decryptions are given out and hence they only “work” for n-out-of-n access structures. Unfortunately, this leads to situations where every secret key owner in the system represents a single point of failure, since if their partial decryption is not given out, it is not possible to recover the output. This is sufficient for protocols only achieving security with abort, as this security notion allows the functionality to fail if even a single party misbehaves. If we want to create schemes that are capable of handling failures, we would necessarily want one to be able to decrypt even when one only possesses a subset of partial decryptions (say t out of n).
At first glance, it seems that our goal is simply incompatible with the notion of multi-key FHE. For instance, suppose that a ciphertext encrypting m under a public key pk can be combined with two public keys \(pk'\) and \(pk''\), and “expanded” into a ciphertext encrypting m under a 2-out-of-3 threshold under the triple of public keys \(\{pk, pk', pk''\}\). Such a feature would imply the insecurity of the original encryption, since an adversary could sample the public keys \(\{pk',pk''\}\) together with their secret keys \(\{sk',sk''\}\), and then use the two secret keys \(\{sk',sk''\}\) to obtain m using the expanded ciphertext.
In order to solve this problem, we introduce a new notion of threshold multi-key FHEFootnote 1 where ciphertexts cannot be “expanded.” Instead, in our notion, given a collection of public keys \(\{pk_1, \dots , pk_n\}\), it is possible for an encryptor to encrypt a message m with respect to an access pattern such as t-out-of-n. Then this ciphertext would only be decryptable by combining partial decryptions obtained from holders of at least t corresponding secret keys. As we show in this work, it turns out that this functionality is sufficient for obtaining new applications to MPC (see below for details).
In this work, we first formally define threshold multi-key FHE in a general way, and then we show to construct this new primitive from the learning with errors (LWE) assumption. Formally, we show the following theorem:
Theorem 1 (Informal)
Assuming LWE, there exists a secure threshold multi-key FHE scheme for the class of access structures \(\mathbb {A}\) induced by all monotone boolean formulas.
In Sect. 2, we describe the challenges and techniques involved in our construction. Our next contribution is an application of threshold multi-key FHE in the context of round-optimal secure MPC protocols with guaranteed output delivery (GOD).
1.2 Application to Round-Optimal MPC
Secure multi-party computation (MPC) [23, 36, 37] has been a problem of fundamental interest in cryptography. In an MPC protocol, a set of mutually distrusting parties can evaluate a function on their joint inputs while maintaining privacy of their respective inputs. Over the last few decades, much of the work related to MPC has been devoted to achieving stronger security guarantees and improving efficiency with respect to various parameters such as round complexity and communication complexity. In this work, we further advance our understanding of this landscape with threshold multi-key FHE being the main technical tool.
MPC Supporting “Honest but Lazy” Parties. In traditional MPC, every party is required to remain online and participate completely in the protocol execution. This applies not only to “classical” MPC protocols where every party has to participate and send a message in every round of the protocol, but also to other interesting variants such as protocols in the client-server setting where all the servers are required to remain active until the end of the protocol execution. We refer the reader to Sect. 1.4 for a more detailed comparison with related works. In other words, traditional MPC protocols decide to treat a “lazy” party that just aborts midway into the protocol execution as a corrupt party that is colluding with the other corrupt parties, and this is addressed in different ways. In some cases, all parties abort the protocol execution while in other cases, the “lazy” party is just discarded and all the other parties compute the function on their joint inputs alone. We believe that such an outlook is undesirable as there are several reasons why even an honest party might have to abort and become “lazy” during the execution of a protocol without having to be deemed as colluding with the corrupt parties. A few potential reasons include:
-
Connectivity - A party might lose connectivity and hence be unable to continue the protocol.
-
Computational resources - A computationally weak party might be unable to perform intensive computation and hence be forced to exit the protocol.
-
Interest - At some point, a party might just lose interest in that protocol execution due to other higher priority tasks that come up.
Motivated by the above realistic scenarios, we would like to construct MPC protocols that can handle “honest but lazy” parties without simply lumping them in with the other corrupted parties (since treating all aborting parties as “malicious” will unrealistically enhance the power of the adversary and limit our protocol’s capabilities). Furthermore, we would like our protocol to be robust to aborting parties (that is, have guaranteed output delivery). Informally, this means that at the end of the protocol execution, regardless of the behavior of the adversary, the honest parties can still compute the output of the function on all their joint inputs (with either a default or the actual input for each of the corrupted parties). Ideally, we would like to achieve a stronger form of guaranteed output delivery, where, when possible, the output of the protocol is with respect to the actual input of all the “honest but lazy” parties, rather than some default input. This is akin to stating that provided an “honest but lazy” party actually sent a message dependent on its input, the protocol will compute the functionality with respect to this party’s input, regardless of whether or not the party aborted during the rest of the protocol. We call this property input fidelity. In this work, we ask
Can we construct round-optimal protocols in the plain model that achieve the above desiderata?
If such protocols are achievable, then
Can these protocols handle the maximum number of possible corruptions?
What can we say about the assumptions, communication complexity, and reusability of such protocols?
Using our new primitive, threshold multi-key FHE, we are able to answer all the above satisfactorily. We construct the first round-optimal (three-round) MPC protocol in the plain model that achieves our desired properties. Moreover, our protocol is capable on handling the maximum number of corruptions that a protocol can possibly support while achieving the desired properties. Our protocol relies only on the learning with errors (LWE) assumption. Furthermore, our protocol has depth-proportional communication complexity and is reusable.
Formalizing Our Desired Properties. Formally, we study MPC with guaranteed output delivery in the presence of threshold mixed adversaries, introduced by Fitzi et al. [19, 20]. In this setting, a threshold mixed adversary \({\mathcal {A}} \) is allowed to corrupt three sets of parties \(({\mathcal {A}} _\mathbf{Mal },{\mathcal {A}} _\mathbf{Sh },{\mathcal {A}} _\mathbf{Fc })\) such that the following holds: (i) \(|{\mathcal {A}} _\mathbf{Mal }| \le t_\mathbf{Mal }\), \(|{\mathcal {A}} _\mathbf{Sh }| \le t_\mathbf{Sh }\), and \(|{\mathcal {A}} _\mathbf{Fc }| \le t_\mathbf{Fc }\), for a tuple of thresholds \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\). (ii) The set of parties in \({\mathcal {A}} _\mathbf{Mal }\) are maliciously corrupted meaning that the adversary can choose to behave using any arbitrary polynomial time algorithm on behalf of each of them. (iii) The set of parties in \({\mathcal {A}} _\mathbf{Sh }\) are corrupted in a semi-honest manner and so the adversary is required to follow the protocol execution honestly on behalf of each of them. (iv) The set of parties in \({\mathcal {A}} _\mathbf{Fc }\) are corrupted in a fail-corrupt manner meaning that for each party in this set, the adversary can specify when that party is required to abort the protocol execution. Until then, these parties follow the protocol execution honestly. Note that the adversary never gets to see the inputs or internal state of any of the fail-corrupt parties and hence these parties capture our motivation of “honest but lazy” parties - where their laziness is enforced by the adversary in the security game.
In this work, our goal is to build a round-optimal MPC protocol with guaranteed output delivery in this model that also simultaneously satisfies the following desirable properties:
-
Security Against the Maximum Number of Corruptions: Security should hold against a threshold mixed adversary that can corrupt the maximum number of parties under which guaranteed output delivery is achievable.
-
Input Fidelity: In line with our motivation, we want our protocol to satisfy not only guaranteed output delivery, but also the stronger property that the output of the computation is a function of the joint inputs of all parties, including those that aborted after a “certain point”. Intuitively, we would like our protocol to be divided into two phases - an input commitment phase and a computation phase. We refer to the end of the input commitment phase as this “point.” That is, in the scenario where the adversary corrupts a set of parties in a fail-corrupt manner, for every fail-corrupt party \(P_i\) that aborts after the input commitment phase, its input \(y_i\) that is used to compute the final output \(C(y_1,\ldots ,y_n)\) is set to be its actual input \(x_i\) used in the protocol so far and not a default input \(\bot \). Recall that this aligns with our original motivation where we wish to not discard honest but lazy parties and deem them to be corrupt.
-
Depth-Proportional Communication Complexity: For any function f, the communication complexity of the protocol should be \(\mathsf {poly}(\lambda ,d,N, \ell _\mathsf {inp})\) where N is the number of parties, \(\lambda \) is the security parameter, \(\ell _\mathsf {inp}\) is the input length for each party, d is the depth of the circuit computing f.
-
Reusability: Given the transcript of the input commitment phase of the protocol, the computation phase of the protocol should be able to be reused across an unbounded polynomial number of executions to compute different functions on the same fixed joint inputs of all the parties.
Prior to our work, much of the focus in this model was on obtaining feasibility results, understanding under what corruption patterns is secure computation even possible, and improving the communication complexity. We refer to Sect. 1.4 for a more detailed discussion on the prior work in this model. In particular, Hirt et al. [27] showed that in the setting of a threshold mixed adversary, MPC with guaranteed output delivery is possible if and only if \(2t_\mathbf{Mal }+ t_\mathbf{Sh }+ t_\mathbf{Fc }< N\), where N is the total number of parties. Since we are interested in guaranteed output delivery, we focus on constructing MPC protocols that are secure against \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\)-threshold mixed adversaries, for any \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\) satisfying the above inequality. Furthermore, in light of the result of Gordon et al. [24] showing that three rounds are required for MPC with guaranteed output delivery in the traditional model (this can be viewed as a special case of the threshold mixed adversary model, where \(t_\mathbf{Sh }\) and \(t_\mathbf{Fc }\) are both 0), we observe that a three round protocol will be round-optimal in this setting.
Utilizing our new primitive, threshold multi-key FHE, given any tuple of thresholds \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\) satisfying the Hirt et al. [27] inequality, we construct the first round-optimal (three-round) MPC protocol with guaranteed output delivery that is secure against such a threshold mixed adversary. Since guaranteed output delivery is possible if and only if the Hirt et al. [27] inequality holds, our resulting protocol is optimal in terms of the best possible corruption we can tolerate. The first two rounds of our protocol form the input commitment phase, and round 3 is the computation phase. Our protocol has input fidelity, in the sense that the functionality is computed with respect to the inputs of all parties that did not abort in the first two rounds, even if that party aborts in round three. Additionally, given the transcript of the input commitment phase (the first two rounds of the protocol), the third round can be reused across an unbounded polynomial number of executions to compute different functions on the same fixed joint inputs of all parties. Our protocol also has depth-proportional communication complexity. Formally, we show the following result:
Theorem 2 (Informal)
Assuming learning with errors (LWE), for any function f on N inputs, for any tuple of thresholds \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\) satisfying \(2t_\mathbf{Mal }+ t_\mathbf{Sh }+ t_\mathbf{Fc }< N\), there exists a three-round MPC protocol with guaranteed output delivery in the plain model that is secure against a \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\)-mixed adversary. The protocol has input fidelity, depth-proportional communication complexity, and is reusable.
By instantiating Theorem 2 with the \((\lceil N/2 - 1 \rceil , 0, 0)\)-mixed adversary we achieve an interesting result in the traditional MPC world in the plain model: in particular, notice that this setting corresponds to an honest majority of parties and as a result, we get a three round MPC protocol in the plain model with guaranteed output delivery. As mentioned previously, our protocol is round optimal for this setting as well due to the lower bound of Gordon et al. [24]. Formally, we achieve the following corollary, matching the round complexity of the recent independent work [1], but for the first time, also achieving input fidelity, reusability, and depth-proportional communication complexity, assuming only LWE.
Corollary 1 (Informal)
Assuming LWE, for any function f, there exists a three-round MPC protocol with guaranteed output delivery in the plain model in the presence of an honest majority.
1.3 Multi-string NIZK from LWE
As a stepping stone to achieving Theorem 2, we first consider the weaker setting of a \((t_\mathbf{Sm }, t_\mathbf{Sh }, t_\mathbf{Fc })\)-semi-malicious mixed adversary that corrupts the sets \(({\mathcal {A}} _\mathbf{Sm },{\mathcal {A}} _\mathbf{Sh },{\mathcal {A}} _\mathbf{Fc })\) of parties such that the first set of parties \({\mathcal {A}} _\mathbf{Sm }\), with \(|{\mathcal {A}} _\mathbf{Sm }| \le t_\mathbf{Sm }\), is only corrupted in a semi-malicious manner - that is, on behalf of each party in this set, the adversary can pick any arbitrary randomness of its choice but using this randomness, the party is required to execute the protocol honestly. We define this formally in the technical sections. Once we have constructed a protocol that is secure against a semi-malicious mixed adversary, we are able to bootstrap it to one that is secure against a (malicious) mixed adversary in the plain model using a multi-string non-interactive zero knowledge (NIZK) argument.
In a multi-string NIZK argument system, introduced in the work of Groth and Ostrovsky [25], a set of parties can each generate one CRS that can then be combined to compute one unified CRS which is used to compute NIZKs. The guarantee is that as long as a majority of the individual CRS strings are honestly generated, the argument system is correct and secure. Unfortunately, one of the tools in the construction of multi-string NIZKs in [25] was a Zap [16], which is not known from polynomially hard LWE. In order to obtain Theorem 2 assuming only polynomially hard LWE, we construct a (simulation-extractable) multi-string NIZK directly from LWE, which may be of independent interest. Formally, we show the following.
Theorem 3 (Informal)
Assuming polynomially hard LWE, there exists a simulation-extractable multi-string NIZK for NP.
1.4 Independent and Subsequent Work
We discuss related work in detail in the full version of the paper.
Independent Work. Recently, in an independent work, Ananth et. al [1] also constructed a three-round honest majority MPC protocol with guaranteed output delivery in the plain model, assuming PKE and ZAPs. Their techniques are substantially different from ours, and we note that if we instantiate our protocol with the \((\lceil N/2 - 1\rceil , 0, 0)\) tuple of thresholds, we are able to match their result, assuming LWE, as shown in Corollary 1. Moreover, our protocol simultaneously achieves depth-proportional communication complexity and reusability, properties not achievable by their protocol. Furthermore, we note that our general protocol can handle threshold mixed adversaries, whereas their protocol is only secure against malicious adversaries in the honest majority setting.
Subsequent Works. The work of [15] (which cites us as prior work) can use a threshold PKI model, which is a very strong form of certified PKI model, to achieve some of our results (guaranteed output delivery, depth proportional communication) in 2 rounds. In this work, we do not make any trust assumptions. However, we observe that our protocol already gives a 2-round protocol with a much weaker form of PKI where the public keys can be any arbitrary string. Thus, our work also implies results in a “plain” PKI setting. Last-round reusability, which we achieve, was also not studied in [15]. However, we note that the focus of [15] was to understand adaptive security in the context of communication efficient protocols, which we do not study.
A recent series of works [10, 11, 28, 31, 35] have developed a framework for instantiating the Fiat-Shamir transform [18] using a hash function that satisfies a property called correlation-intractability [12]. This culminated in the work of Peikert and Shiehian [35], who were able to obtain the first NIZK from LWE by constructing a correlation-intractable hash function family for (bounded) circuits from LWE. Following this, there have been two works [2, 30], subsequent to ours, that construct two message statistically witness indistinguishable ZAP arguments from quasipolynomial LWE. From this, using the work of [25] one can construct a multi-string NIZK from quasipolynomial LWE. We obtain a multi-string NIZK argument system assuming only the polynomial hardness of LWE.
2 Technical Overview
We first describe the challenges involved in defining and constructing our new primitive of threshold multi-key FHE in the next subsection. This is followed by the techniques involved in constructing our round-optimal MPC protocol with guaranteed output delivery. Finally, we discuss the techniques used to construct a multi-string NIZK from LWE.
2.1 Threshold Multi-key FHE (TMFHE)
Definitional Challenges. Recall that we would like to construct a version of multi-key FHE that only requires some (say t out of n) of the partial decryption shares in order to reconstruct the output as opposed to all n partial decryptions, as is required in all existing multi-key FHE schemes.
At first glance, it is not even clear how to define such a notion. The most direct approach leads to a definition that is impossible to achieve. Consider for example the n/2-out-of-n access structure. In this case, if we follow the standard procedure used by known multi-key FHE schemes, any evaluator can expand a ciphertext encrypting a message m with respect to public key \(pk_n\) to a ciphertext \(ct\) with respect to the set of public keys \((pk_1,...,pk_n)\). Then, the evaluator can use secret keys \(sk_{1},..,sk_{n/2}\) to learn the value of m, as the set \(\{1\ldots ,n/2\}\) satisfies the access structure. However, in doing so, an adversary can learn m without knowing \(sk_n\), breaking the semantic security of the encryption scheme with respect to \((pk_n,sk_n)\) and leading to a notion that provides no security.
Although we seem to have arrived at a notion that is not meaningful at all, we note that the issue with the above approach is that a ciphertext encrypted with respect to a public key \(pk\) can be expanded to one encrypted with respect to many public keys. However, if we prevent ciphertexts from being expanded, there is hope of achieving a meaningful notion. Expanding on this idea, we arrive at the following (informal) definition. Any party can generate its own key pair \((pk,sk)\). Any encryptor can compute \(ct\leftarrow \mathsf {Encrypt}(pk_1,..,pk_n, \mathbb {A},m)\). Given two (or more) ciphertexts encrypted with respect to the same set of public keys and the same access structure \(\mathbb {A}\), it is possible to homomorphically evaluate a circuit on these ciphertexts and partially decrypt the resulting ciphertext using any secret key \(sk_i\) to recover a partial decryption \(p_i\). Given \(\{p_i\}_{i\in B}\) for some B satisfying \(\mathbb {A}\), one can reconstruct the output. Roughly, we require two security guarantees from the scheme.
-
1.
Given \(\{sk_i\}_{i\in S}\) for some \(S\notin \mathbb {A}\),
$$\mathsf {Encrypt}(pk_1, \ldots ,pk_n, \mathbb {A},m_0)\approx _{c} \mathsf {Encrypt}(pk_1,..,pk_n, \mathbb {A},m_1) $$for any two equal length messages \(m_0,m_1\).
-
2.
Given a ciphertext \(ct\) for an underlying message m and \(\{sk_i\}_{i\in S}\) for any maximally unqualified setFootnote 2 \(S\notin \mathbb {A}\) (for example \((n/2-1)\) of the parties for the example above), it is possible to statistically simulate a partial decryption \(p_i\) for any \(i\in [n]\).
For technical reasons, we require a more nuanced security definition, and we refer the reader to Sect. 4 for the details.
Construction Overview. In order to construct TMFHE, one could try many approaches to build on top of existing multi-key FHE schemes. For example, one could try the following. Given any set of public keys \((pk_1,..,pk_n)\), generate ciphertexts \(ct_{S}\leftarrow \mathsf {Encrypt}(\{pk_{i}\}_{i\in S},m)\) for all minimally valid sets \(S\in \mathbb {A}\). However, such an approach is not feasible for access structures such as \(n/2-\)out-of-n as then the encryptor has to compute encryptions for roughly \(n \atopwithdelims (){n/2}\) subsets, which is super-polynomial.
To overcome this limitation, we use the tool of threshold FHE introduced in the work of Boneh et al. [4]. In a threshold FHE scheme, the setup algorithm samples a single public key \(\mathsf {fpk}\) and n secret key shares \((\mathsf {fsk}_1,..,\mathsf {fsk}_n)\) for a secret key \(\mathsf {fsk}\) that are shared according to the access structure \(\mathbb {A}\). Using the public key \(\mathsf {fpk}\), an encryptor can encrypt a message m to receive a ciphertext \(ct\) (which may be evaluated). This ciphertext can then be partially decrypted independently using key shares \(sk_i\) to compute a partial decryption \(p_i\). Then using these \(\{p_i\}_{i\in S}\) for any set \(S\in \mathbb {A}\), one can recover m. Security properties are two fold:
-
Given \(\{sk_i\}_{i\in S}\) for some \(S\notin \mathbb {A}\), \(\mathsf {Encrypt}(pk, \mathbb {A},m_0)\approx _{c} \mathsf {Encrypt}(pk, \mathbb {A},m_1)\) for any two equal length messages \(m_0,m_1\).
-
Second, given a ciphertext \(ct\) with underlying message m and \(\{sk_i\}_{i\in S}\) for any maximally unqualified \(S\notin \mathbb {A}\), it is possible to statistically simulate partial decryptions \(p_i\) for any \(i\in [n]\).
We make the following useful observations about threshold FHE which will aid us in our construction.
-
1.
The setup algorithm of the scheme of [4] first samples \((pk,sk)\leftarrow \mathsf {FHE}.\mathsf {Setup}(1^{\lambda })\) and then secret shares \(sk\) according to the access structure using a “special purpose” secret sharing scheme to compute shares \((sk_1,..,sk_n)\) so that the reconstruction involves just addition of some subset of shares. Looking ahead to the security proof, this feature allows us to easily simulate partial decryptions.
-
2.
The encryption procedure just involves encrypting the message m using an underlying \(\mathsf {FHE}\) scheme.
-
3.
The underlying \(\mathsf {FHE}\) scheme can be instantiated using most of the known homomorphic encryption schemes satisfying a few general properties.
Thus, we observe that, in particular, the multi-key FHE schemes of both [7, 33], can be used to instantiate the underlying FHE scheme in threshold FHE. This can then be used to evaluate on multiple ciphertexts encrypted with respect to different public keys - since, using multi-key FHE, one can expand on various ciphertexts and evaluate jointly on them. However, at this point, it is still not clear how to compute (or simulate) partial decryptions, especially since the threshold FHE construction of [4] only handled underlying FHE schemes where the ciphertext was encrypted with respect to a single public key. However, we observe the following property of the multi-key FHE schemes of both [7, 33]. Suppose we have two ciphertexts, \(ct_1\) and \(ct_2\) that are encrypted under public keys \(\mathsf {fpk}_1\) and \(\mathsf {fpk}_2\), respectively. In the multi-key FHE scheme, we can expand these ciphertexts to \(\hat{ct}_1\) and \(\hat{ct}_2\), each encrypted under the set of public keys \(\{\mathsf {fpk}_1, \mathsf {fpk}_2\}\). If the secret keys corresponding to \(\mathsf {fpk}_1\) and \(\mathsf {fpk}_2\) are \(\mathsf {fsk}_1\) and \(\mathsf {fsk}_2\), respectively, then the secret key for decryption of \(\hat{ct}_1\) and \(\hat{ct}_2\) (and any ciphertext computed by evaluating on these ciphertexts) is \([\mathsf {fsk}_1, \mathsf {fsk}_2]\). In a standard threshold FHE scheme, the secret key would be secret shared across n parties. For simplicity, assume that we secret share according to the n out of n access structure. Let party i’s shares of \(\mathsf {fsk}_1\) and \(\mathsf {fsk}_2\) be denoted by \(\mathsf {fsk}_{1,i}\) and \(\mathsf {fsk}_{2,i}\), respectively. Since the decryption procedure of the multi-key FHE scheme is linear and the secret sharing of \(\mathsf {fsk}_1\) and \(\mathsf {fsk}_2\) is also linear and, crucially, with respect to the same access structure, one could have party i partially decrypt by running the decryption procedure of the multi-key FHE scheme using the secret key \([\mathsf {fsk}_{1,i}, \mathsf {fsk}_{2,i}]\). Given these partial decryptions, one could combine them to recover the message by adding them as specified by the reconstruction procedure of the secret sharing scheme.
The above gives intuition as to how one might construct threshold multi-key FHE, but several points are still unclear. In particular, we noted that in order to achieve a meaningful notion, we want an encryptor to encrypt with respect to a public key set and an access structure. The idea is that the public key set that an encryptor encrypts with respect to is not a public key set of the underlying MFHE scheme, but rather simply a set of public keys for a public-key encryption scheme. These public keys serve as a means to send the corresponding multi-key FHE secret key shares to the other parties. At a high level, encryption works by generating a multi-key FHE public key \(\mathsf {fpk}\) and secret key shares \(\mathsf {fsk}_1, \ldots , \mathsf {fsk}_n\) corresponding to the access structure \(\mathbb {A}\). The encryptor then encrypts \(\mathsf {fsk}_i\) under \(pk_i\) and includes this in the ciphertext. This allows a set of parties satisfying the access structure to use their secret keys \(sk_i\) of the public-key scheme to recover the necessary \(\mathsf {fsk}_i\)’s to decrypt the ciphertext. Furthermore, as we noted above, standard multi-key FHE expansion and evaluation will result in a ciphertext that can be decrypted by concatenating the secret key shares for each of the ciphertexts.
The above discussion is highly simplified and is meant to provide the reader with some intuition behind our construction. We ignored various subtle points and refer the reader to the main technical sections for the details. As a consequence of our techniques, we are able to directly simulate partial decryptions against an adversary that corrupts any set \(S \not \in \mathbb {A}\), not only a maximally unqualified one. The constructions of [7, 33] could only simulate against a maximally unqualified set (\(N-1\) out of the N parties in their case) and relied on a transformation to achieve simulation security against any unqualified corrupted set.
2.2 MPC with Guaranteed Output Delivery
Recall that a \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\)-threshold mixed adversary is one which corrupts three sets of parties \(({\mathcal {A}} _\mathbf{Mal },{\mathcal {A}} _\mathbf{Sh },{\mathcal {A}} _\mathbf{Fc })\) with \(|{\mathcal {A}} _\mathbf{Mal }| \le t_\mathbf{Mal }\), \(|{\mathcal {A}} _\mathbf{Sh }| \le t_\mathbf{Sh }\), and \(|{\mathcal {A}} _\mathbf{Fc }| \le t_\mathbf{Fc }\) that behave as follows: the set of parties in \({\mathcal {A}} _\mathbf{Mal }\) are completely malicious and can behave arbitrarily as per the adversary’s choice, the set of parties in \({\mathcal {A}} _\mathbf{Sh }\) are corrupted in a semi-honest manner meaning that they are required to follow the protocol behavior correctly and the set of parties in \({\mathcal {A}} _\mathbf{Fc }\) are corrupted in a fail-corrupt manner meaning that for each party in this set, the adversary can choose to abort the protocol execution at any point. Crucially, the adversary does not get to see the internal state of any fail-corrupt party. Intuitively, we can imagine these fail-corrupt parties as honest “lazy” parties whose aborting/laziness is controlled by the adversary. In this work, we focus on the setting of static corruptions where the adversary is required to specify all three sets apriori. Of course, note that for each fail-corrupt party, the adversary still has the luxury to determine adaptively when each party is expected to abort.
Our three-round MPC protocol secure against a threshold mixed adversary follows the same recipe as in the works of Mukherjee and Wichs [33] and Brakerski et al. [7] who construct MPC protocols from multi-key FHE. We adapt it to instead use the underlying system as a threshold multi-key FHE scheme. Further, we will parametrize our protocol using an access structure \(\mathbb {A}\) which will be used to run the setup of the threshold multi-key FHE scheme. Recall that since we are interested in the setting where guaranteed output delivery is possible, we require that \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\) respect the Hirt et al. [27] inequality. That is, \(2t_\mathbf{Mal }+ t_\mathbf{Sh }+ t_\mathbf{Fc }< N\). In our protocol, given a threshold tuple (\(t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\), \(\mathbb {A}\) will be set as the \((N - t_\mathbf{Mal }- t_\mathbf{Fc })\)-out-of-N access structure. This ensures that \(t_\mathbf{Mal }+ t_\mathbf{Sh }\), the maximum number of parties for which the adversary can view the internal state is less than the required threshold to satisfy the access structure.
Security Against Semi-Malicious Mixed Adversaries. Let’s first consider the simpler setting where the first set of corrupted parties \({\mathcal {A}} _\mathbf{Mal }\) can only be semi-malicious. That is, on behalf of each of them, the adversary can pick randomness of its choice but the parties are required to follow the protocol behavior honestly using this randomness. The adversary may also choose to have these parties abort at any time. A more formal definition is given in the full version. The overall structure of our MPC protocol with respect to any access structure is the following:
-
In round 1, each party generates its parameters and public key for the threshold multi-key FHE scheme.
-
In round 2, each party individually encrypts its input with respect to the combined set of public keys and access structure and broadcasts the ciphertext.
-
All parties can now homomorphically compute a threshold multi-key FHE encryption of the output, with respect to the functionality under consideration. Then, each party broadcasts a partial decryption of the output using its secret key. The partial decryptions can be combined to recover the output in plaintext.
It can be readily observed from the definition of threshold multi-key FHE that this protocol satisfies correctness and security even in the presence of a threshold mixed adversary (with semi-malicious corruptions), where some lazy honest parties could drop off from the protocol execution at any point as determined by the fail-corrupt corruption. Furthermore, the fact that the protocol has guaranteed output delivery can be observed by noting that at most \(t_\mathbf{Mal }+ t_\mathbf{Fc }\) parties will abort. So, at least \(N - t_\mathbf{Mal }- t_\mathbf{Fc }\) parties will remain, which is sufficient to recover the output. Note that since we have restricted the adversary to behave semi-maliciously instead of maliciously on the set \({\mathcal {A}} _\mathbf{Mal }\), every message sent will be “valid.”
One key difference from the previous works [7, 33] is the following: in the standard model MPC protocols of [7, 33], due to the design of the multi-key FHE primitive, the protocol is secure only against a semi-malicious adversary that corrupts all but one party. They then need to transform it to a protocol that is secure against an adversary that can corrupt any arbitrary number of parties up to all but one of them. In our MPC protocol, the security guarantee given by the threshold multi-key FHE scheme allows us to prove a more general statement that our protocol is in fact secure even if the adversary chooses to corrupt fewer parties than it is capable of (it chooses to corrupt less than the threshold number of parties).
Handling Malicious Adversaries. The final step in achieving our MPC protocol is to allow the set \({\mathcal {A}} _\mathbf{Mal }\) to be maliciously corrupted. One way to do this would be to use a NIZK and have each party send a proof in each round that they computed their message properly; if the NIZK proof does not verify, the party would be treated as malicious and ignored. Unfortunately, using a NIZK would require us to introduce a CRS, and we want our protocol to be in the plain model.
Round One: Malicious. To do so, the first crucial observation we make is that the underlying semi-malicious protocol (without a NIZK) in the plain model is already in fact secure against an adversary that can behave maliciously only in the first round. The reason is that the first round message, which consists of the adversary’s parameters for the threshold multi-key FHE scheme, is simply a random matrix and a public key. To argue semi-malicious security, we only needed the following two properties:
-
The honest parties’ matrices are generated uniformly at random.Footnote 3
-
The simulator, before the beginning of round three, only needs to know the randomness used by the adversary in the second round to generate its ciphertext. In particular, the simulator does not need to know a corresponding secret key for the public key sent by the adversary in round 1.
As a result, we did not require the input or randomness used by the adversary to generate its round one messages, and hence our protocol is secure against an adversary that can behave maliciously in round one.
Multi-string NIZK. Armed with the above property, we note that our protocol no longer needs to prove correctness of round one messages using a NIZK. Therefore, we will use the first round messages of all parties to try to collectively generate a valid CRS that can then be used to generate the NIZKs and achieve a construction in the plain model. The notion of multi-string NIZKs, introduced in the work of Groth and Ostrovsky [25] exactly fits this requirement. As discussed previously, in a multi-string NIZK argument system, a set of parties can each generate one CRS that can then be combined to compute one unified CRS which is used to compute NIZKs. The guarantee is that as long as a majority of the individual CRS strings are honestly generated, the argument system is correct and secureFootnote 4.
In our protocol, we can use this primitive as follows: in round 1, each party generates an individual CRS for the multi-string NIZK system. At the end of round 1, all parties can combine the above set of CRS strings to compute one unified CRS that can then be used to compute NIZKs. In rounds 2 and 3, each party also sends a NIZK along with their message, and the other parties make sure the NIZK verifies. If the NIZK does not verify, the party that submitted an invalid message is ignored for the rest of the protocol and treated as if it had aborted instead.
There is one additional hurdle to ensuring that a multi-string NIZK suffices for our setting. The multi-string NIZK is only secure if a majority of the CRSs are honestly generated. However, we want our protocol to be secure against any \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\)- mixed adversary, where \(2t_\mathbf{Mal }+ t_\mathbf{Sh }+ t_\mathbf{Fc }< N\). In particular, we need the multi-string NIZK to be secure in settings without an honest majority! Fortunately, the multi-string NIZK is still secure in our setting, provided that the CRSs are uniformly random strings. To see why this is the case, we first observe that \(t_\mathbf{Fc }\), the number of fail-corrupt parties does not present any difficulties. This is because these parties fall under the “honest but lazy” parties in our motivation, and so while the adversary can force them to abort, the adversary can never learn any internal state information of these parties or cause them to behave dishonestly. Therefore, any CRS output by these parties will be an honest CRS, and so choosing to not have these parties abort prior to round 1 only increases the number of honest CRSs that are output. The second observation is that any semi-honest corruptions also do not cause any difficulties. This is because the honest procedure for generating a CRS is to simply sample a random string. Therefore, even if an adversary semi-honestly corrupts a party, it can neither prevent it from outputting an honestly generated random string nor learn any state information that could compromise the random string. Therefore, all the CRSs output by the semi-honest corrupt and fail-corrupt parties are honest, and since \(2t_\mathbf{Mal }+ t_\mathbf{Sh }+ t_\mathbf{Fc }< N\), it follows that a majority of the CRSs are honestly generated. Therefore, security of the multi-string NIZK system holds and we obtain a plain model construction. In this work, we construct a multi-string NIZK from LWE that satisfies this additional property required of the CRS and we elaborate more on this construction now.
2.3 Multi-string NIZK from LWE
The above demonstrated that a simulation-extractable multi-string NIZK would allow us to obtain our round-optimal MPC protocol. However, a multi-string NIZK is not known to exist from LWE. Previously it was known from statistically sound ZAPS as shown in the work of [25]. However, ZAPs are not known to exist from polynomially hard LWE. One might think that we could use the recent result of Peikert and Shiehian [35], which constructs either a statistically-sound NIZK in the common reference string model or a computationally-sound NIZK in the common random string model. One might think that we could use the transformation of Dwork and Naor [16] to obtain a ZAP from LWE and then apply the transformation of [25]. However, this does not work, since their transformation crucially requires a statistically-sound NIZK in the common random string model, which is not known from polynomially hard LWE (the recent works of [2, 30] construct such ZAPs from quasipolynomial LWE). Therefore, we require a different approach. We construct the first multi-string NIZK from LWE and use it as a tool in obtaining our round-optimal MPC result.
Our construction proceeds in two main steps. We first build a multi-string non-interactive witness indistinguishable (NIWI) argument from LWE and then show how to bootstrap it to obtain a simulation-extractable multi-string NIZK.
A recent series of works [10, 11, 28, 31, 35] have developed a framework for instantiating the Fiat-Shamir transform [18] using a hash function that satisfies a property called correlation-intractability [12]. This culminated in the work of Peikert and Shiehian [35], who were able to obtain the first NIZK from LWE by constructing a correlation-intractable hash function family for (bounded) circuits from LWE. The notion of a correlation-intractable hash function family is defined formally in the full version. Informally, a hash function family \(\mathcal {H}\) is correlation-intractable for a relation \(\mathcal {R}\) if given a sampled key K, it is hard to find an x such that \((x, \mathcal {H}_K(x)) \in \mathcal {R}\). Following the formula introduced in the above works, we will apply the Fiat-Shamir transform to the \(\varSigma \) protocol for Graph Hamiltonicity by Blum [3] in order to obtain our multi-string NIZK.
Multi-string NIWI from LWE. The first step is to construct a multi-string NIWI from LWE. A multi-string NIWI is defined analogously to a multi-string NIZK. That is, in a multi-string NIWI, a set of parties can each generate one CRS that can then be combined to compute one unified CRS which is used to compute NIWIs. The guarantee is that as long as a majority of the individual CRS strings are honestly generated, the argument system is correct and secure.
To construct the multi-string NIWI, we first construct a non-interactive commitment scheme in the multi-string model with the property that the scheme remains hiding and binding provided that a majority of the CRSs are honestly generated. At a high level, this is done by having each CRS be a public key \(pk_i\) of a public key encryption (PKE) scheme. To commit to a message m, one simply secret shares m using a \(\lfloor n/2 \rfloor + 1\)-out-of-n secret sharing scheme to obtain shares \((m_1, \ldots , m_n)\), then encrypts \(m_i\) under \(pk_i\), and outputs these n ciphertexts as the commitment. Since a majority of the public keys were generated honestly, a majority of the shares are hidden by the encryption, so the commitment scheme satisfies hiding. By the correctness of the PKE scheme, the resulting commitment scheme must also be binding. Furthermore, we observe that this commitment scheme also has an associated trapdoor that facilitates extraction of the message committed. In particular, any majority of the secret keys \(sk_i\) can be used as a trapdoor as they can recover a majority of message shares from the commitment and, therefore, the message.
The multi-string NIWI is built by having each party generate its CRS in the setup phase as a public key \(pk_i\) of a PKE scheme and a hash key \(K_i\) from the correlation hash function family \(\mathcal {H}\). To prove a statement \(x \in L\) using a witness w, we run \(\lambda \) parallel repetitions of the \(\varSigma \) protocol using the above commitment scheme as the underlying commitment scheme and making it non-interactive via the Fiat-Shamir transformation, with the hash function instantiated using \(\mathcal {H}_{K_i}\). A proof is the transcript of all the parallel executions of the \(\varSigma \) protocol. Soundness follows from the correlation-intractability of the hash function family \(\mathcal {H}\), the binding property of the commitment scheme and the soundness of the underlying \(\varSigma \) protocol. Witness indistinguishability follows from the witness indistinguishability of the underlying \(\varSigma \) protocol and the fact that the commitment scheme is hiding even if a minority of shares are learned. We refer the reader to the full version for more details.
Obtaining a Multi-string NIZK. In order to obtain a multi-string NIZK from our multi-string NIWI, we use the standard trick found in [17, 25] each party also generates a random string \(r_i\) as part of their CRS and the statement that is proven using the multi-string NIWI now is that \(x \in L\) OR a majority of the \(r_i\)’s are actually the output of a pseudorandom generator \(\mathsf {G}\). Soundness and zero knowledge then follow via standard arguments, and we refer the reader to the full version for more details. We then observe that we can also prove simulation-extractability of our multi-string NIZK if we additionally use the commitment scheme from before once again and require the prover to commit to its witness using this scheme. The statement being proved using the multi-string NIWI would now be that either \(x \in L\) using a witness w that was committed OR a majority of the \(r_i\)’s are actually the output of a pseudorandom generator \(\mathsf {G}\). Further, in order to prove that the scheme is simulation extractable, here, we will instantiate all the underlying PKE schemes inside the extra commitment scheme (for the witness) with CCA-secure PKE schemes. As a result, our extractor for the simulation-extractable NIZK can use the secret keys of all the honest parties for this extra commitment scheme as a trapdoor to learn the witness associated with the adversary’s proof. We refer the reader to the full version for more details about the proof.
Finally, recall that in order to use the multi-string NIZK in our MPC protocol, we require that the CRS generated by each party is a uniformly random string. However, in our construction, in addition to the random string r, the CRS consists of two public keys (one for committing to the witness and one for the commitment used in the \(\varSigma \) protocol) and a hash key K for a correlation-intractable hash function family \(\mathcal {H}\). We will use an encryption scheme whose public keys are statistically-close to uniform and we also observe that the hash key is statistically-close to uniform. This ensures that the CRS is also statistically-close to uniform. We then prove that this is in fact sufficient for the MPC application and we don’t require the CRS to be a uniformly random string. We refer to the full version for more details.
Roadmap. We define some preliminaries in Sect. 3. Then, we formally define threshold multi-key FHE in Sect. 4 and give our construction in Sect. 5. In Sect. 6, we describe our round optimal MPC protocol with guaranteed output delivery against threshold mixed adversaries. Finally, in Sect. 7, we construct multi-string NIZKs.
3 Preliminaries
We denote the security parameter by \(\lambda \). For an integer \(n \in \mathbb {N}\), we use [n] to denote the set \(\{1,2, \ldots , n\}\). We use \(\mathcal {D}_0 \cong _c \mathcal {D}_1\) to denote that two distributions \(\mathcal {D}_0, \mathcal {D}_1\) are computationally indistinguishable. We use \(\mathsf {negl}(\lambda )\) to denote a function that is negligible in \(\lambda \). We use \(x \leftarrow \mathcal {A}\) to denote that x is the output of a randomized algorithm \(\mathcal {A}\), where the randomness of \(\mathcal {A}\) is sampled from the uniform distribution. We use PPT as an abbreviation for probabilistic polynomial-time. Whenever we write \(\{x_j\}_{j \in S}\) for a set of parties S, we assume that the party j that \(x_j\) corresponds to is included in S. When we say an error distribution is E-bounded, we mean that the errors are in \([-E, E]\).
Cryptographic Primitives. We formally define secret sharing, correlation intractable hash functions, simulation-extractable multi-string NIZKs, and Sigma protocols in the full version. We also define MPC against a threshold mixed adversary with guaranteed output delivery following the works of [19, 20] in the full version of the paper.
Guaranteed Output Delivery (GOD). Consider an MPC protocol \(\pi \) amongst N parties. Informally, \(\pi \) is said to possess guaranteed output delivery (GOD) if for every PPT malicious adversary, for all possible sets of inputs \(\{x_1,\ldots ,x_N\}\), for any function f, the following holds: At the end of the execution of \(\pi \), every honest party outputs \(f(y_1,\ldots ,y_n)\) where \(y_i = x_i\) for every honest party \(P_i\) and \(y_j = x_j/ \bot \) for every corrupt party \(P_j\).
3.1 Multi-key FHE
We recall the definition of multi-key FHE in the plain model with distributed setup as found in [7].
Definition 1 (MFHE)
A multi-key fully homomorphic encryption scheme is a tuple of PPT algorithms
satisfying the following specifications:
-
\(\mathsf {params}_i \leftarrow \mathsf {DistSetup}(1^\lambda , 1^d, 1^N, i)\): It takes as input a security parameter \(\lambda \), a circuit depth d, the maximal number of parties N, and a party index i. It outputs the public parameters \(\mathsf {params}_i\) associated with the ith party, where \(\mathsf {params}_i \in \{0,1\}^{\mathsf {poly}(\lambda , d, N)}\) for some polynomial \(\mathsf {poly}\). We assume implicitly that all the following algorithms take the public parameters of all parties as input, where we define \(\mathsf {params}= \mathsf {params}_1||\ldots ||\mathsf {params}_N\).
-
\((pk, sk) \leftarrow \mathsf {KeyGen}(\mathsf {params})\): It takes as input the public parameters \(\mathsf {params}\) and outputs a key pair \((pk, sk)\).
-
\(ct\leftarrow \mathsf {Encrypt}(pk, m)\): It takes as input a public key pk and a plaintext \(m \in \{0, 1\}^\lambda \) and outputs a ciphertext ct. Throughout, we will assume that all ciphertexts include the public key(s) that they are encrypted under.
-
\(\widehat{ct} \leftarrow \mathsf {Eval}(C, ct_1, \dots , ct_\ell )\): It takes as input a boolean circuit \(C:(\{0,1\}^\lambda )^\ell \rightarrow \{0, 1\} \in \mathcal {C}_\lambda \) of depth \(\le d\) and ciphertexts \(ct_1, \dots , ct_\ell \) for \(\ell \le N\). It outputs an evaluated ciphertext \(\widehat{ct}\).
-
\(p_i \leftarrow \mathsf {PartDec}(i, sk, \hat{ct})\): It takes as input an index i, a secret key \(sk\) and an evaluated ciphertext \(\hat{ct}\) and outputs a partial decryption \(p_i\).
-
\(\widehat{\mu }\leftarrow \mathsf {FinDec}(p_1, \ldots , p_\ell )\): It takes as input partial decryptions \(p_1, \ldots , p_\ell \) and deterministically outputs a plaintext \(\widehat{\mu }\in \{0, 1, \bot \}\).
We require that for any parameters \(\{\mathsf {params}_i \leftarrow \mathsf {Setup}(1^\lambda , 1^d, 1^N, i)\}_{i \in [N]}\), any key pairs \(\{(pk_i, sk_i) \leftarrow \mathsf {KeyGen}(\mathsf {params})\}_{i \in [N]}\), any plaintexts \(m_1, \dots , m_\ell \in \{0, 1\}^\lambda \) for \(\ell \le N\), any sequence \(I_1, \ldots , I_{\ell } \in [N]\) of indices, and any boolean circuit \(C:\{0, 1\}^\ell \rightarrow \{0, 1\}\in \mathcal {C}_\lambda \) of depth \(\le d\), the following is satisfied:
-
Correctness. Let \(ct_i=\mathsf {Encrypt}(pk_{I_i}, m_i)\) for \(1\le i\le \ell \), \(\hat{ct} = \mathsf {Eval}(C, ct_1, \dots , ct_\ell )\), and \(p_i =\mathsf {PartDec}(i, sk_{I_i}, \hat{ct})\) for all \(i \in [\ell ]\). With all but negligible probability in \(\lambda \) over the coins of \(\mathsf {Setup}\), \(\mathsf {KeyGen}\), \(\mathsf {Encrypt}\), and \(\mathsf {PartDec}\),
$$\begin{aligned} \mathsf {FinDec}(p_1, \ldots , p_\ell ) = C(m_1, \dots , m_\ell ). \end{aligned}$$ -
Compactness of Ciphertexts. There exists a polynomial, \(\mathsf {poly}\), such that \(\left| ct\right| \le \mathsf {poly}(\lambda , d, N)\) for any ciphertext \(ct\) generated from the algorithms of \(\mathsf {MFHE}\).
-
Semantic Security of Encryption. Any PPT adversary \(\mathcal {A}\) has only negligible advantage as a function of \(\lambda \) over the coins of all the algorithms in the following game:
-
1.
On input the security parameter \(1^{\lambda }\), a circuit depth \(1^d\), and the number of parties \(1^N\), the adversary \(\mathcal {A}\) outputs a non-corrupted party i.
-
2.
Run \(\mathsf {DistSetup}(1^{\lambda },1^d, 1^N, i)\rightarrow \mathsf {params}_i\). The adversary is given \(\mathsf {params}_i\).
-
3.
The adversary outputs \(\{\mathsf {params}_j\}_{j \in [N] \backslash \{i\}}\).
-
4.
\(\mathsf {params}\) is set to \(\mathsf {params}_1||\ldots ||\mathsf {params}_N\). Run \(\mathsf {KeyGen}(\mathsf {params}) \rightarrow (pk_i, sk_i)\). The adversary is given \(pk_i\).
-
5.
The adversary outputs two messages \(m_0, m_1 \in \{0,1\}^\lambda \).
-
6.
The adversary is given \(ct\leftarrow \mathsf {Encrypt}(pk_i, m_b)\) for a random \(b \in \{0,1\}\).
-
7.
The adversary outputs \(b'\) and wins if \(b=b'\).
-
1.
-
Simulation Security. There exists a stateful PPT algorithm \(\mathsf {Sim}\) such that for any PPT adversary \(\mathcal {A}\), we have that the experiments \(\mathsf {Expt}_{\mathcal {A},Real}(1^{\lambda },1^d, 1^N)\) and \(\mathsf {Expt}_{\mathcal {A}, \mathsf {Sim}}(1^{\lambda },1^d, 1^N)\) as defined below are statistically close as a function of \(\lambda \) over the coins of all the algorithms. The experiments are defined as follows:
-
\(\mathsf {Expt}_{\mathcal {A},Real}(1^{\lambda },1^d, 1^N) \):
-
1.
On input the security parameter \(1^{\lambda }\), a circuit depth \(1^d\), and the number of parties \(1^N\), the adversary \(\mathcal {A}\) a non-corrupted party i.
-
2.
Run \(\mathsf {DistSetup}(1^{\lambda },1^d,1^N, i)\rightarrow \mathsf {params}_i\). The adversary is given \(\mathsf {params}_i\).
-
3.
The adversary outputs \(\{\mathsf {params}_j\}_{j \in [N] \backslash \{i\}}\).
-
4.
\(\mathsf {params}\) is set to \(\mathsf {params}_1||\ldots ||\mathsf {params}_N\). Sample \(N-1\) key pairs \(\mathsf {KeyGen}(\mathsf {params}) \rightarrow (pk_j, sk_j)\) for \(j \in [N] \backslash \{i\}\). The adversary is given \(\{(pk_j, sk_j)\}_{j \in [N] \backslash \{i\}}\).
-
5.
The adversary outputs randomness \(r_i^{\mathsf {KeyGen}}\) used to generate \((pk_i, sk_i)\), \(m_1, \ldots , m_\ell \in \{0,1\}^\lambda \), \(I_1, \ldots , I_\ell \in [N]\), and a set of circuits \(\{C_k: (\{0,1\}^\lambda )^\ell \rightarrow \{0,1\}\}_{k \in [t]}\) with each \(C_k \in \mathcal {C}\) for some \(\ell \le N\) and some \(t = \mathsf {poly}(\lambda , d, N)\).
-
6.
Set \((pk_i, sk_i) \leftarrow \mathsf {KeyGen}(\mathsf {params}; r_i^{\mathsf {KeyGen}})\). The adversary is given \(ct_j \leftarrow \mathsf {Enc}(pk_{I_j}, m_j)\) for \(1 \le j \le \ell \) and the evaluated ciphertexts \(\hat{ct}_k \leftarrow \mathsf {Eval}(C_k, ct_1, \ldots , ct_\ell )\) for all \(k \in [t]\).
-
7.
The adversary is given \(p_{i,k} \leftarrow \mathsf {PartDec}(i, sk_i, \hat{ct}_k)\) for all \(k \in [t]\).
-
8.
\(\mathcal {A}\) outputs \(\mathsf {out}\). The output of the experiment is \(\mathsf {out}\).
-
1.
-
\(\mathsf {Expt}_{\mathcal {A},\mathsf {Sim}}(1^{\lambda },1^d, 1^N) \):
-
1.
On input the security parameter \(1^{\lambda }\), a circuit depth \(1^d\), and the number of parties \(1^N\), the adversary \(\mathcal {A}\) a non-corrupted party i.
-
2.
Run \(\mathsf {DistSetup}(1^{\lambda },1^d,1^N, i)\rightarrow \mathsf {params}_i\). The adversary is given \(\mathsf {params}_i\).
-
3.
The adversary outputs \(\{\mathsf {params}_j\}_{j \in [N] \backslash \{i\}}\).
-
4.
\(\mathsf {params}\) is set to \(\mathsf {params}_1||\ldots ||\mathsf {params}_N\). Sample \(N-1\) key pairs \(\mathsf {KeyGen}(\mathsf {params}) \rightarrow (pk_j, sk_j)\) for \(j \in [N] \backslash \{i\}\). The adversary is given \(\{(pk_j, sk_j)\}_{j \in [N] \backslash \{i\}}\).
-
5.
The adversary outputs randomness \(r_i^{\mathsf {KeyGen}}\) used to generate \((pk_i, sk_i)\), \(m_1, \ldots , m_\ell \in \{0,1\}^\lambda \), \(I_1, \ldots , I_\ell \in [N]\), and a set of circuits \(\{C_k: (\{0,1\}^\lambda )^\ell \rightarrow \{0,1\}\}_{k \in [t]}\) with each \(C_k \in \mathcal {C}\) for some \(\ell \le N\) and some \(t = \mathsf {poly}(\lambda , d, N)\).
-
6.
Set \((pk_i, sk_i) \leftarrow \mathsf {KeyGen}(\mathsf {params}; r_i^{\mathsf {KeyGen}})\). The adversary is given \(ct_j \leftarrow \mathsf {Enc}(pk_{I_j}, m_j)\) for \(1 \le j \le \ell \) and the evaluated ciphertexts \(\hat{ct}_k \leftarrow \mathsf {Eval}(C_k, ct_1, \ldots , ct_\ell )\) for all \(k \in [t]\).
-
7.
Define \(\mu _k = C_k(m_1, \ldots , m_\ell )\). For all \(k \in [t]\), the adversary is given \(p_{i,k} \leftarrow \mathsf {Sim}(\mu _k, \hat{ct}, i, \{sk_j\}_{j \in [N] \backslash \{i\}})\).
-
8.
\(\mathcal {A}\) outputs \(\mathsf {out}\). The output of the experiment is \(\mathsf {out}\).
-
1.
-
4 Threshold Multi-key FHE: Definition
In this section, we present the definition of threshold multi-key fully homomorphic encryption (TMFHE) in the plain model with distributed setupFootnote 5. TMFHE will be the main building block in our MPC protocol.
Definition 2 (TMFHE)
Let \(P=\{P_1, \dots , P_N\}\) be a set of parties and let \(\mathbb {S}\) be a class of efficient access structures on P. A threshold multi-key fully homomorphic encryption scheme supporting up to N parties is a tuple of PPT algorithms
satisfying the following specifications:
-
\(\mathsf {params}_i \leftarrow \mathsf {DistSetup}(1^\lambda , 1^d, 1^N, i)\): It takes as input a security parameter \(\lambda \), a circuit depth d, the maximal number of parties N, and a party index i. It outputs the public parameters \(\mathsf {params}_i\) associated with the ith party. We define \(\mathsf {params}= \mathsf {params}_1||\ldots ||\mathsf {params}_N\).
-
\((pk, sk) \leftarrow \mathsf {KeyGen}(1^\lambda )\): It takes as input the security parameter \(\lambda \) and outputs a key pair \((pk, sk)\).
-
\(ct\leftarrow \mathsf {Encrypt}(\mathsf {params}, pk_1, \ldots , pk_N, \mathbb {A}, m)\): It takes as input the public parameters \(\mathsf {params}\), public keys \(pk_1, \ldots , pk_N\), an access structure \(\mathbb {A}\) over P and a plaintext \(m\in \{0, 1\}^\lambda \) and outputs a ciphertext \(ct\). Throughout, we will assume that all ciphertexts include the public parameters, the public keys, and the access structure that they are encrypted under.
-
\(\widehat{ct} \leftarrow \mathsf {Eval}(C, ct_1, \dots , ct_\ell )\): It takes as input a boolean circuit \(C:(\{0,1\}^\lambda )^\ell \rightarrow \{0, 1\} \in \mathcal {C}_\lambda \) of depth \(\le d\) and ciphertexts \(ct_1, \dots , ct_\ell \) for \(\ell = \mathsf {poly}(N)\). It outputs an evaluated ciphertext \(\widehat{ct}\).
-
\(p_i \leftarrow \mathsf {PartDec}(i, sk, \hat{ct})\): It takes as input an index i, a secret key \(sk\) and an evaluated ciphertext \(\hat{ct}\) and outputs a partial decryption \(p_i\).
-
\(\widehat{\mu }\leftarrow \mathsf {FinDec}(B)\): It takes as input a set \(B=\{p_i \}_{i\in S}\) for some \(S\subseteq \{P_1, \dots , P_N\}\) where we recall that we identify a party \(P_i\) with its index i. It deterministically outputs a plaintext \(\widehat{\mu }\in \{0, 1, \bot \}\).
We require that for any parameters \(\{\mathsf {params}_i \leftarrow \mathsf {DistSetup}(1^\lambda , 1^d, 1^N, i)\}_{i \in [N]}\), any key pairs \(\{(pk_i, sk_i) \leftarrow \mathsf {KeyGen}(1^\lambda )\}_{i \in [N]}\), any supported access structure \(\mathbb {A}\) over P, any plaintexts \(m_1, \dots , m_\ell \in \{0, 1\}^\lambda \) for \(\ell = \mathsf {poly}(N)\), and any boolean circuit \(C:(\{0, 1\}^\lambda )^\ell \rightarrow \{0, 1\}\in \mathcal {C}_\lambda \) of depth \(\le d\), the following is satisfied:
-
Correctness. Let \(ct_i=\mathsf {Encrypt}(\mathsf {params}, pk_1, \ldots , pk_N, \mathbb {A}, m_i)\) for \(1\le i\le \ell \), \(\hat{ct} = \mathsf {Eval}(C, ct_1, \dots , ct_\ell )\), and \(B =\{\mathsf {PartDec}(i, sk_i, \hat{ct})\}_{i \in S}\). With all but negligible probability in \(\lambda \) over the coins of \(\mathsf {DistSetup}\), \(\mathsf {KeyGen}\), \(\mathsf {Encrypt}\), and \(\mathsf {PartDec}\),
$$\begin{aligned} \mathsf {FinDec}(B) = {\left\{ \begin{array}{ll} C(m_1, \dots , m_\ell ), &{} S\in \mathbb {A}\\ \bot &{} S\not \in \mathbb {A}. \end{array}\right. } \end{aligned}$$ -
Compactness of Ciphertexts. There exists a polynomial, \(\mathsf {poly}\), such that \(\left| ct\right| \le \mathsf {poly}(\lambda , d, N)\) for any ciphertext \(ct\) generated from the algorithms of \(\mathsf {TMFHE}\).
-
Simulation Security. There exist PPT algorithms \(\mathsf {Sim}_1, \mathsf {Sim}_2\) such that for any PPT adversary \(\mathcal {A}\), we have that the experiments \(\mathsf {Expt}_{\mathcal {A},Real}(1^{\lambda },1^d, 1^N)\) and \(\mathsf {Expt}_{\mathcal {A}, \mathsf {Sim}}(1^{\lambda },1^d, 1^N)\) are computationally indistinguishable.
-
\(\mathsf {Expt}_{\mathcal {A},Real}(1^{\lambda },1^d, 1^N) \):
-
1.
On input the security parameter \(1^{\lambda }\), a circuit depth \(1^d\), and the maximal number of parties \(1^N\), the adversary \(\mathcal {A}\) outputs an access structure \(\mathbb {A}\in \mathbb {S}\) over N parties and a maximal set \(S \subseteq [N]\) such that \(S \not \in \mathbb {A}\).
-
2.
For \(i \in [N]\), run \(\mathsf {DistSetup}(1^{\lambda },1^d,1^N, i)\rightarrow \mathsf {params}_i\). The adversary is given \(\{\mathsf {params}_i\}_{i \in [N]}\). Sample key pairs \(\mathsf {KeyGen}(1^\lambda ) \rightarrow (pk_i, sk_i)\) for \(i \in [N]\). The adversary is given \(\{pk_i\}_{i \in [N]}\) and \(\{sk_i\}_{i \in S}\).
-
3.
The adversary then outputs messages \(m_1, \ldots , m_{\ell } \in \{0,1\}^\lambda \) for \(\ell = \mathsf {poly}(N)\).
-
4.
\(\mathsf {params}\) is set to the concatenation of the \(\mathsf {params}_i\)’s for \(i \in [N]\). Let \(\mathcal {PK}= \{pk_i\}_{i \in [N]}\). The adversary is given \(ct_i \leftarrow \mathsf {Enc}(\mathsf {params}, \mathcal {PK}, \mathbb {A}, m_i)\) for \(i \in [\ell ]\).
-
5.
The adversary issues polynomially many queries of the form \((C_k: (\{0,1\}^\lambda )^{\ell } \rightarrow \{0,1\})\), where \(C_k \in \mathcal {C}\). Let the evaluated ciphertext be \(\hat{ct}_k \leftarrow \mathsf {Eval}(C_k, ct_1, \ldots , ct_\ell )\). After each query, the adversary receives \(p_{i,k} \leftarrow \mathsf {PartDec}(i, sk_i, \hat{ct}_k)\) for all \(i \in [N]\backslash S\).
-
6.
\(\mathcal {A}\) outputs \(\mathsf {out}\). The output of the experiment is \(\mathsf {out}\).
-
1.
-
\(\mathsf {Expt}_{\mathcal {A},Sim}(1^{\lambda },1^d, 1^N) \):
-
1.
On input the security parameter \(1^{\lambda }\), a circuit depth \(1^d\), and the maximal number of parties \(1^N\), the adversary \(\mathcal {A}\) outputs an access structure \(\mathbb {A}\in \mathbb {S}\) over N parties and a maximal set \(S \subseteq [N]\) such that \(S \not \in \mathbb {A}\).
-
2.
For \(i \in [N]\), run \(\mathsf {DistSetup}(1^{\lambda },1^d,1^N, i)\rightarrow \mathsf {params}_i\). The adversary is given \(\{\mathsf {params}_i\}_{i \in [N]}\). Sample key pairs \(\mathsf {KeyGen}(1^\lambda ) \rightarrow (pk_i, sk_i)\) for \(i \in [N]\). The adversary is given \(\{pk_i\}_{i \in [N]}\) and \(\{sk_i\}_{i \in S}\).
-
3.
The adversary then outputs messages \(m_1, \ldots , m_{\ell } \in \{0,1\}^\lambda \) for \(\ell = \mathsf {poly}(N)\).
-
4.
\(\mathsf {params}\) is set to the concatenation of the \(\mathsf {params}_i\)’s for \(i \in [N]\). Let \(\mathcal {PK}= \{pk_i\}_{i \in [N]}\). The adversary is given \(\{ct_i\}_{i \in [\ell ]} \leftarrow \mathsf {Sim}_1(\mathsf {params}, \mathcal {PK}, \mathbb {A})\).
-
5.
The adversary issues polynomially many queries of the form \((C_k: (\{0,1\}^\lambda )^{\ell } \rightarrow \{0,1\})\), where \(C_k \in \mathcal {C}\). Let the evaluated ciphertext be \(\hat{ct}_k \leftarrow \mathsf {Eval}(C_k, ct_1, \ldots , ct_\ell )\). After each query, the adversary receives \(\{p_{i,k}\}_{i \not \in S} \leftarrow \mathsf {Sim}_2(\mu _k, \hat{ct}_k, S, \{sk_i\}_{i \in S})\), where \(\mu _k = C_k(\{m_i\}_{i \in [\ell ]})\).
-
6.
\(\mathcal {A}\) outputs \(\mathsf {out}\). The output of the experiment is \(\mathsf {out}\).
-
1.
-
The security notion is inspired by the security definitions of multi-key FHE [7, 33] suitably adapted to the context of general access structures. Observe that the above definition captures both the semantic security of ciphertexts and the simulation security of partial decryptions.
Looking ahead to our MPC protocol, we will actually need some stronger guarantees from the TMFHE scheme, which adds complexity to the security definition. In our MPC protocol, the adversary is allowed to choose which honest parties abort in each round and is rushing, so he is allowed to control the randomness of corrupted parties as a function of the honest parties. We capture this by allowing the simulator of the TMFHE scheme to be stateful. Additionally, since the adversary in MPC is rushing, it is allowed to see the honest parameters/ciphertexts before it picks its parameters/ciphertexts.
The (more general) formal definition we use is deferred to the full version.
5 Threshold Multi-key FHE: Construction
In this section, we construct threshold multi-key FHE as defined in Sect. 4. Formally, we show the following.
Theorem 4 (TMFHE)
Assuming LWE, there exists a secure threshold multi-key FHE scheme for the class of access structures \(\{0, 1\}\text {-}\mathsf {LSSSD}\). In particular, there exists a secure TMFHE scheme for any access structure induced by a monotone boolean formula and any \(t \text { out of } N\) access structure.
We use several ingredients. First, we initialize a multi-key FHE scheme using the construction in [7]. Then, we utilize the techniques in the construction of threshold FHE in [29]Footnote 6, which shows how to transform a generic FHE scheme satisfying several properties into a threshold FHE scheme. We observe that the multi-key FHE construction of [7] is “compatible” with the thresholdizing transformation described in [29]. Finally, we use a public key encryption scheme to tie everything together.
In more detail, examining the construction of [29], we note that it is compatible with a generic FHE scheme where:
-
1.
The secret key \(sk\) is a vector in \(\mathbb {Z}_q^m\) for some prime q.
-
2.
The decryption function \(\mathsf {Dec}\) can be broken into two algorithms \(\mathsf {Dec}_0, \mathsf {Dec}_1\) where \(\mathsf {Dec}_0(sk, ct)\) computes a linear function in \(sk\) and \(ct\) to output \(\mu \left\lceil q/2 \right\rceil + e\) for some bounded error \(e \in [-E, E]\) with \(E<< q\), where \(ct\) is an encryption of \(\mu \). \(\mathsf {Dec}_1\) then takes this resulting value and rounds to recover \(\mu \).
We note that the construction of multi-key FHE in [7] satisfies these required properties. Furthermore, it satisfies the following additional properties that will be useful to note in the construction.
-
1.
An evaluated ciphertext \(\hat{ct}\) that encrypts a bit \(\mu \) with respect to public keys \(pk_1, \ldots , pk_\ell \) is a matrix that satisfies
$$ \mathbf {s} \cdot \hat{ct} \approx \mu \mathbf {s} \cdot G $$for a gadget matrix G and \(\mathbf {s} = (sk_1 || \ldots || sk_\ell )\), where \(sk_i\) is the secret key corresponding to public key \(pk_i\). Each \(sk_i\) is of the form \((s_i || 1)\).
-
2.
There exists a low-norm vector \(\mathbf {v}\) such that \(G\mathbf {v} = (0, 0, \ldots , \left\lceil q/2 \right\rceil )^T\). Decryption proceeds by evaluating \(\mathbf {s} \cdot \hat{ct} \cdot \mathbf {v}\) and then outputs 1 if the resulting value is closer to \( \left\lceil q/2 \right\rceil \) than 0 and 0 otherwise.
Furthermore, [29] shows the following result.
Theorem 5
([29]). For any access structure \(\mathbb {A}\) on N parties induced by a monotone boolean formula, there exists a \(\{0, 1\}\text {-}\mathsf {LSSSD}\) scheme of a vector \(s \in \mathbb {Z}_q^m\) where each party \(P\) receives at most w shares of the form \(s_i \in \mathbb {Z}_q^m\) for \(w = \mathsf {poly}(N)\).
5.1 Construction
Let \(\mathsf {MFHE}= (\mathsf {DistSetup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {PartDec}, \mathsf {FinDec})\) be a multi-key FHE scheme instantiated with the construction in [7]. Let \(\mathsf {PKE}= (\mathsf {Setup}, \mathsf {Enc}, \mathsf {Dec})\) be a public-key encryption scheme. Let \(\chi ^{sm}\) denote the uniform distribution on the interval \([-E_{sm}, E_{sm}]\) for a value \(E_{sm}\) to be determined.
Our threshold multi-key FHE construction \(\mathsf {TMFHE}\) is given as follows:
-
\(\mathsf {DistSetup}(1^\lambda , 1^d, 1^N, i)\): Run \(\mathsf {MFHE}.\mathsf {DistSetup}(1^\lambda , 1^d, 1^N, i) \rightarrow \mathsf {params}_i\) and output \(\mathsf {params}_i\).
-
\(\mathsf {KeyGen}(1^\lambda )\): Run \(\mathsf {PKE}.\mathsf {Setup}(1^\lambda ) \rightarrow (pk, sk)\) and output \((pk, sk)\).
-
\(\mathsf {Encrypt}(\mathsf {params}, pk_1, \ldots , pk_N, \mathbb {A}, m)\): Run \(\mathsf {MFHE}.\mathsf {KeyGen}(\mathsf {params}) \rightarrow (\mathsf {fpk}, \mathsf {fsk})\). Compute \(\{\mathsf {fsk}_{i,j}\}_{i \in [N], j \in [w]}\) for some \(w = \mathsf {poly}(N)\) by applying the \(\{0, 1\}\text {-}\mathsf {LSSSD}\) scheme associated with \(\mathbb {A}\) to \(\mathsf {fsk}\) to . Set \(ct' \leftarrow \mathsf {MFHE}.\mathsf {Enc}(\mathsf {fpk}, m)\) and for \(i \in [N]\), set \(ct_i = \mathsf {PKE}.\mathsf {Enc}(pk_i, \{\mathsf {fsk}_{i,j}\}_{j \in [w]})\). Output
$$ ct= (ct', ct_1, \ldots , ct_N). $$ -
\(\mathsf {Eval}(C, ct_1, \ldots , ct_{\ell })\): Parse \(ct_i\) as \((ct'_i, ct_{i, 1}, \ldots , ct_{i,N})\). Let \(\mathsf {fpk}_i\) be the \(\mathsf {MFHE}\) public key associated with \(ct'_i\). Run \(\mathsf {MFHE}.\mathsf {Eval}(C, ct'_1, \ldots , ct'_{\ell }) \rightarrow \hat{ct}'\). Output
$$ \hat{ct} = (\hat{ct'}, \{ct_{i,j}\}_{(i,j) \in [\ell ] \times [N]}). $$ -
\(\mathsf {PartDec}(i, sk, \hat{ct})\): Parse \(\hat{ct}\) as \((\hat{ct'}, \{ct_{k,j}\}_{(k,j) \in [\ell ] \times [N]})\). For every \(k \in [\ell ]\), run \(\mathsf {PKE}.\mathsf {Dec}(sk, ct_{k, i}) \rightarrow \{\mathsf {fsk}_{k,i,j}\}_{j \in [w]}\). For \(t \in [w]\), compute
$$ (\mathsf {fsk}_{1, i, t}||\mathsf {fsk}_{2,i, t}||\ldots ||\mathsf {fsk}_{\ell ,i, t}) \cdot \hat{ct'} \cdot \mathbf {v} + e_t^{sm} \rightarrow p'_t, $$where \(e_t^{sm} \leftarrow \chi ^{sm}\) and \(\mathbf {v}\) is the low-norm vector used for decryption in [7] described above. Output \(p_i = (i,\{p'_t\}_{t \in [w]})\).
-
\(\mathsf {FinDec}(B)\): Parse B as \(\{(i,\{p'_t\}_{t \in [w]})\}_{i \in S}\) for some set S of indices. If \(S \not \in \mathbb {A}\), output \(\bot \). If \(S \in \mathbb {A}\), apply the \(\{0, 1\}\text {-}\mathsf {LSSSD}\) reconstruction to get \(\approx \hat{\mu } \left\lceil q/2 \right\rceil \). Then, round to recover \(\hat{\mu }\).
We defer the proofs of correctness, compactness, and security to the full version.
Instantiation. In order for correctness to hold, we required that \(E + Nw E_{sm} < q/4\). For security, we required that \(NwE/E_{sm} = \mathsf {negl}(\lambda )\). Recall that \(w = \mathsf {poly}(N)\). Let \(W = \mathsf {poly}(N)\) be an upper bound for the set of access structures supported by the scheme. Then, setting \(E/E_{sm} < \lambda ^{-\log _2 \lambda }\) and \(E_{sm} < q/8NW\) gives us an instantiation that satisfies both correctness and security. The MFHE scheme of [7] can be instantiated with such properties assuming a variant of the learning with errors assumption, which is as hard as approximating the shortest vector problem to within a subexponential factor.
6 Round-Optimal MPC with Guaranteed Output Delivery Secure Against Threshold Mixed Adversaries
In this section, we use threshold multi-key FHE to construct a round-optimal (three-round) MPC protocol in the plain model with guaranteed output delivery that is secure against a threshold mixed adversary (defined in the full version), assuming LWE. Our protocol supports all functionalities computable by polynomial-sized circuits and is parameterized by a tuple of thresholds \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\) that represent the number of malicious, semi-honest, and fail-corrupt corruptions that the adversary is allowed to make, respectively. Our protocol has guaranteed output delivery and is secure provided that \(2t_\mathbf{Mal }+ t_\mathbf{Sh }+ t_\mathbf{Fc }< N\), the Hirt et al. [27] inequality that characterizes the threshold values under with guaranteed output delivery is possible to achieve.
Thus, our resulting protocol is both optimal in terms of the best possible corruption we can tolerate and also round-optimal (since at least three rounds are required for a protocol to have guaranteed output delivery, as shown by Gordon et al. [24]). Moreover, our protocol has depth-proportional communication complexity, is reusable, and has input fidelity for “honest but lazy” parties. Formally, we show the following.
Theorem 6
Assuming LWE, for any function f, for any tuple of thresholds \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\) satisfying \(2t_\mathbf{Mal }+ t_\mathbf{Sh }+ t_\mathbf{Fc }< N\), there exists a three-round MPC protocol with guaranteed output delivery in the plain model that is secure against a \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\)-mixed adversary. Furthermore, the protocol is reusable, has communication complexity \(\mathsf {poly}(\lambda , d, N)\), where d is the depth of the circuit computing f and the functionality is computed with respect to the inputs of all parties that send valid messages in the first two rounds.
Note that our result in the mixed adversary setting is in fact broader and more general than the traditional MPC setting. By instantiating Theorem 6 with the \((\lceil N/2 - 1\rceil , 0, 0)\)-mixed adversary (this corresponds to the honest-majority setting against a malicious adversary), we immediately obtain the following corollary.
Corollary 2
Assuming LWE, for any function f, there exists a three-round MPC protocol with guaranteed output delivery in the plain model that is secure against a malicious adversary in the honest majority setting. Furthermore, the protocol is reusable and has communication complexity \(\mathsf {poly}(\lambda , d, N)\), where d is the depth of the circuit computing f.
Like Theorem 6, this result is round-optimal and supports the maximum possible number of corruptions.
6.1 Security Against a Semi-malicious Mixed Adversary
As a stepping stone to showing Theorem 6, we first construct a protocol that satisfies all the properties of Theorem 6, except that it is only secure against a semi-malicious mixed adversary (defined in the full version), which is simply a mixed adversary that corrupts some parties semi-maliciously, rather than maliciously. We describe below our three-round MPC protocol that is secure against a \((t_\mathbf{Sm }, t_\mathbf{Sh }, t_\mathbf{Fc })\)-semi-malicious mixed adversary \({\mathcal {A}} = ({\mathcal {A}} _\mathbf{Sm },{\mathcal {A}} _\mathbf{Sh },{\mathcal {A}} _\mathbf{Fc })\) for \(2t_\mathbf{Sm }+ t_\mathbf{Sh }+ t_\mathbf{Fc }< N\).
Notation: Consider N parties \(P_1,\ldots ,P_N\) with inputs \(x_1,\ldots , x_N\), respectively, who wish to evaluate a boolean circuit \(C\) with depth \(\le d\). Without loss of generality, assume \(|x_i| = \lambda \ \forall i \in [N]\). Let \((\mathsf {DistSetup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {PartDec}, \mathsf {FinDec})\) be the previously constructed threshold multi-key FHE scheme. Fix \((t_\mathbf{Sm }, t_\mathbf{Sh }, t_\mathbf{Fc })\) satisfying \(2t_\mathbf{Sm }+ t_\mathbf{Sh }+ t_\mathbf{Fc }< N\). Let \(\mathbb {A}\) be the \((N - t_\mathbf{Sm }- t_\mathbf{Fc })\)-out-of-N threshold access structure.
Protocol: We now describe our construction.
-
Input Commitment Phase:
-
\(\bullet \) Round 1: Each party \(P_i\) does the following:
-
1.
Run \(\mathsf {TMFHE}.\mathsf {DistSetup}(1^\lambda , 1^d, 1^N, i)\) to obtain \(\mathsf {params}_i\).
-
2.
Run \(\mathsf {TMFHE}.\mathsf {KeyGen}(1^\lambda )\) to compute \((pk_i, sk_i)\).
-
3.
Output \((\mathsf {params}_i, pk_i)\).
-
1.
-
\(\bullet \) Round 2: Each party \(P_i\) does the following:
-
1.
Parse the message (if one was sent) from \(P_j\) as \((\mathsf {params}_j, pk_j)\). Let \(S_1 \subseteq [N]\) be the set of parties that sent a message in round 1.
-
2.
Truncate each \(\mathsf {params}_j\) for \(j \in S_1\) to the appropriate size given \(|S_1|\)Footnote 7. Set \(\mathsf {params}\) as the concatenation of the truncated \(\mathsf {params}_j\)’s for \(j \in S_1\). Set \(\mathcal {PK}= \{pk_j\}_{j \in S_1}\). Let \(\mathbb {A}'\) be the access structure induced by restricting \(\mathbb {A}\) to the parties in \(S_1\) (that is, the \((N - t_\mathbf{Sm }- t_\mathbf{Fc })\)-out-of-\(|S_1|\) access structure).
-
3.
Run \(\mathsf {TMFHE}.\mathsf {Encrypt}(\mathsf {params}, \mathcal {PK}, \mathbb {A}', x_i)\) to compute \(ct_i\).
-
4.
Output \(ct_i\).
-
1.
-
-
Computation Phase:
-
\(\bullet \) Round 3: Each party \(P_i\) does the following:
-
1.
Parse the previous message (if one was sent) from \(P_j\) as \(ct_j\). Let \(S_2 \subseteq [N]\) be the set of parties that sent a message in round 2. Let \(\mathcal {CT}= \{ct_j\}_{j \in S_2}\). Let \(C'\) be the circuit induced by hardcoding the inputs to C corresponding to parties not in \(S_2\) to be \(0^\lambda \).
-
2.
Run \(\mathsf {TMFHE}.\mathsf {Eval}(C', \mathcal {CT})\) to obtain \(\hat{ct}\).
-
3.
Run \(\mathsf {TMFHE}.\mathsf {PartDec}(i, sk_i, \hat{ct})\) to obtain \(p_i\).
-
4.
Output \(p_i\).
-
1.
-
-
Output Computation: Each party \(P_i\) does the following:
-
1.
Parse the previous message (if one was sent) from \(P_j\) as \(p_j\). Let \(S_3 \subseteq [N]\) be the set of parties that sent a message in round 3.
-
2.
Take any set \(S \subseteq S_3\) with \(S \in \mathbb {A}\) and run \(\mathsf {TMFHE}.\mathsf {FinDec}(B)\) where \(B = \{p_j\}_{j \in S}\) to recover \(\hat{\mu }\). If no such set exists, output \(\bot \).
-
1.
We defer the proofs of correctness, security, and the properties of the above protocol to the full version.
6.2 Handling a Malicious Mixed Adversary
In the above protocol, the adversary can only corrupt some subset \({\mathcal {A}} _\mathbf{Sm }\) of the parties semi-maliciously, some subset \({\mathcal {A}} _\mathbf{Sh }\) in a semi-honest manner and another subset \({\mathcal {A}} _\mathbf{Fc }\) in a fail-corrupt manner. In order to show Theorem 6, we need to allow the adversary to corrupt the first subset \({\mathcal {A}} _\mathbf{Sm }\) maliciously.
Our first observation is that the protocol is secure even against mixed adversaries that are allowed make parties in \({\mathcal {A}} _\mathbf{Sm }\) behave maliciously in round 1, but only semi-maliciously in rounds 2 and 3. After noting this, we further observe that if we had a simulation-extractable multi-string NIZK [25] in the plain model where the honest party’s behavior when generating a CRS is to simply sample a uniformly random stringFootnote 8, then we could upgrade to security against malicious mixed adversaries. We simply have each party send a reference string CRS in round 1 and then require each party to also provide a NIZK argument in rounds 2 and 3 using these CRSs to ensure that they submitted a valid message in that round. As mentioned previously, the multi-string NIZK is only secure if a majority of the CRSs are honestly generated. However, we want our protocol to be secure against any \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\)- mixed adversary, where \(2t_\mathbf{Mal }+ t_\mathbf{Sh }+ t_\mathbf{Fc }< N\). In particular, we are no longer in the honest majority setting. As discussed earlier, this is not an issue because only the CRSs corresponding to a maliciously-corrupted party could be dishonestly generated and since the honest-generation behavior is to simply output a uniformly random string, a party that is semi-honestly corrupted will also output a perfectly good CRS. Furthermore, since the number of maliciously-corrupted parties is a minority of the total number of parties that send a CRS, a majority of the CRSs will be honestly generated and security of the multi-string NIZK holds.
Security Against a Round 1 Malicious Mixed Adversary. We begin by showing security of the protocol in Sect. 6.1 against a semi-malicious mixed adversary that can behave maliciously in round 1. Since \(\mathsf {params}_i\) in the MFHE construction in [7] is simply a matrix \(A_i\) of random entries, it follows that every \(A_i\) output of a malicious adversary could also have been output by a semi-malicious adversary that chose the appropriate randomness (we can simply truncate the message or pad it with 0’s if the malicious adversary sends a message of inappropriate length). However, a malicious adversary may send a \(pk_i\) that does not correspond to any possible public key output by the \(\mathsf {TMFHE}.\mathsf {KeyGen}\) algorithm. So, in the proof, the simulator does not receive the randomness \(r_i^{\mathsf {KeyGen}}\) used by the adversary to compute the round 1 message for a corrupted party and therefore does not receive \(sk_i\) for corrupted parties. However, as we saw in Sect. 5, the simulator does not need to know \(sk_i\) or \(r_i^{\mathsf {KeyGen}}\). Rather, it suffices to know \((x_i, r_i^{\mathsf {Encrypt}})\), the input and randomness used to compute a corrupted party’s round 2 message in order to simulate. Thus, an analogous simulator and proof can be used to show security against this adversary.
Upgrading to Malicious Security via Multi-string NIZKs. We now show how to use a simulation-extractable multi-string NIZK with uniformly random CRSs to upgrade the protocol in Sect. 6.1 to one that achieves Theorem 6. The final step is to show that such a multi-string NIZK can be built from LWE. This was not previously known, and we show this in Sect. 7.
Construction. Let \(\mathsf {TMFHE}= (\mathsf {DistSetup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {PartDec}, \mathsf {FinDec})\) be the previously constructed threshold multi-key FHE scheme from Sect. 5 with the underlying PKE scheme instantiated with one where any string is a valid public key (a dense cryptosystem). Fix \((t_\mathbf{Mal }, t_\mathbf{Sh }, t_\mathbf{Fc })\) satisfying \(2t_\mathbf{Mal }+ t_\mathbf{Sh }+ t_\mathbf{Fc }< N\). Let \(\mathbb {A}\) be the \(N - t_\mathbf{Mal }- t_\mathbf{Fc }\)-out-of-N threshold access structure. Let \(\mathsf {NIZK}= (\mathsf {Gen}, \mathsf {Prove}, \mathsf {Verify})\) be a simulation-extractable multi-string NIZK. To compare against our previous protocol in Sect. 6.1, we highlight the changes in red.
-
Round 1: Each party \(P_i\) does the following:
-
1.
Run \(\mathsf {TMFHE}.\mathsf {DistSetup}(1^\lambda , 1^d, 1^N, i)\) to obtain \(\mathsf {params}_i\).
-
2.
Run \(\mathsf {TMFHE}.\mathsf {KeyGen}(1^\lambda )\) to compute \((pk_i, sk_i)\).
-
3.

-
4.
Output
 .
.
-
1.
-
Round 2: Each party \(P_i\) does the following:
-
1.
Parse the message (if one was sent) from \(P_j\) as
 by appropriately truncating or padding with 0’s if it was of incorrect length. Let \(S_1 \subseteq [N]\) be the set of parties that sent a message in round 1.
by appropriately truncating or padding with 0’s if it was of incorrect length. Let \(S_1 \subseteq [N]\) be the set of parties that sent a message in round 1. -
2.
Truncate each \(\mathsf {params}_j\) for \(j \in S_1\) to the appropriate size given \(|S_1|\). Set \(\mathsf {params}\) as the concatenation of the truncated \(\mathsf {params}_j\)’s for \(j \in S_1\). Set \(\mathcal {PK}= \{pk_j\}_{j \in S_1}\).
 . Let \(\mathbb {A}'\) be the access structure induced by restricting \(\mathbb {A}\) to the parties in \(S_1\) (that is, the \((N - t_\mathbf{Sm }- t_\mathbf{Fc })\)-out-of-\(|S_1|\) access structure).
. Let \(\mathbb {A}'\) be the access structure induced by restricting \(\mathbb {A}\) to the parties in \(S_1\) (that is, the \((N - t_\mathbf{Sm }- t_\mathbf{Fc })\)-out-of-\(|S_1|\) access structure). -
3.
Sample randomness \(r_i\) and run \(\mathsf {TMFHE}.\mathsf {Encrypt}(\mathsf {params}, \mathcal {PK}, \mathbb {A}', x_i; r_i)\) to compute \(ct_i\).
-
4.
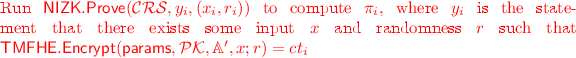 .
. -
5.
Output
 .
.
-
1.
-
Round 3: Each party \(P_i\) does the following:
-
1.
Parse the previous message (if one was sent) from \(P_j\) as
 and
and
 Let \(S_2 \subseteq S_1\) be the set of parties that sent a message in round 2 that passed the verification. Let \(\mathcal {CT}= \{ct_j\}_{j \in S_2}\). Let \(C'\) be the circuit induced by hardcoding the inputs to C corresponding to parties not in \(S_2\) to be \(0^\lambda \).
Let \(S_2 \subseteq S_1\) be the set of parties that sent a message in round 2 that passed the verification. Let \(\mathcal {CT}= \{ct_j\}_{j \in S_2}\). Let \(C'\) be the circuit induced by hardcoding the inputs to C corresponding to parties not in \(S_2\) to be \(0^\lambda \). -
2.
Run \(\mathsf {TMFHE}.\mathsf {Eval}(C', \mathcal {CT})\) to compute \(\hat{ct}\).
-
3.
Sample randomness \(r'_i\) and run \(\mathsf {TMFHE}.\mathsf {PartDec}(i, sk_i, \hat{ct}; r'_i)\) to compute \(p_i\).
-
4.

-
5.
Output
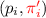 .
.
-
1.
-
Output Computation: Each party \(P_i\) does the following:
-
1.
Parse the previous message (if one was sent) from \(P_j\) as
 and
and
 . Let \(S_3 \subseteq S_2\) be the set of parties that sent a message in round 3 that passed verification.
. Let \(S_3 \subseteq S_2\) be the set of parties that sent a message in round 3 that passed verification. -
2.
Take any set \(S \subseteq S_3\) with \(S \in \mathbb {A}'\) and run \(\mathsf {TMFHE}.\mathsf {FinDec}(B)\) where \(B = \{p_j\}_{j \in S}\) to recover \(\hat{\mu }\). If no such set exists, output \(\bot \).
-
1.
We defer the formal proofs to the full version.
7 Multi-string NIZKs
In this section, we build a simulation-extractable multi-string NIZK argument system for NP based on the learning with errors (LWE) assumption. We first show how to build a multi-string non-interactive witness indistinguishable argument system (NIWI) from LWE. We then give a transformation from multi-string NIWI to multi-string simulation-extractable NIZK that follows along the lines of the work of Groth and Ostrovsky [25]. Formally, we show the following results:
Theorem 7
Assuming LWE, there exists a multi-string non-interactive witness indistinguishable argument system for NP.
Theorem 8
Assuming LWE, there exists a multi-string simulation-extractable NIZK argument system for NP.
We defer this section to the full version.
Notes
- 1.
We remark that in fact, some existing standard multi-key FHE schemes [33] also sometimes used the term threshold multi-key FHE to refer to their primitive, which requires an n-out-of-n threshold. We will use threshold multi-key FHE to denote only our stronger notion supporting general thresholds.
- 2.
By maximally unqualified set S, we mean that for any \(i \in [n]{\setminus }S\), \((S \cup \{i\}) \in \mathbb {A}\). Similarly, a set S is minimally qualified if for any \(i \in [S]\), \((S{\setminus }\{i\}) \notin \mathbb {A}\).
- 3.
This was a wonderful observation made in the work of Brakerski et al. [7].
- 4.
As is the case with compiling semi-malicious protocols into malicious secure ones, we need the NIZK to be simulation-extractable.
- 5.
- 6.
- 7.
Note that the \(\mathsf {params}_i\) of each party in the MFHE construction in [7] and, therefore, also in our TMFHE construction, are simply random matrices \(A_i\) of a size dependent on N. Therefore, truncating the matrix to the appropriate size for a scheme with \(|S_1|\) parties is equivalent to having run the distributed setup algorithm for \(|S_1|\) parties.
- 8.
For ease of exposition, we assume here that the honest CRS is a uniformly random string. However, there is a subtle technical issue, which we handle in Sect. 7 where we construct the multi-string NIZK.
References
Ananth, P., Choudhuri, A.R., Goel, A., Jain, A.: Round-optimal secure multiparty computation with honest majority. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 395–424. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_14
Badrinarayanan, S., Fernando, R., Jain, A., Khurana, D., Sahai, A.: Statistical ZAP arguments. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 642–667. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_22
Blum, M.: How to prove a theorem so no one else can claim it. In: Proceedings of the International Congress of Mathematicians. vol. 1, p. 2. Citeseer (1986)
Boneh, D., et al.: Threshold cryptosystems from threshold fully homomorphic encryption. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10991, pp. 565–596. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_19
Boneh, D., Gennaro, R., Goldfeder, S., Kim, S.: A lattice-based universal thresholdizer for cryptographic systems. IACR Cryptol. ePrint Arch. 2017, 251 (2017). http://eprint.iacr.org/2017/251
Brakerski, Z., Gentry, C., Vaikuntanathan, V.: (leveled) fully homomorphic encryption without bootstrapping. In: ITCS, pp. 309–325 (2012)
Brakerski, Z., Halevi, S., Polychroniadou, A.: Four round secure computation without setup. In: Theory of Cryptography (2017)
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. In: FOCS, pp. 97–106 (2011)
Brakerski, Z., Vaikuntanathan, V.: Fully homomorphic encryption from Ring-LWE and security for key dependent messages. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 505–524. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_29
Canetti, R., et al.: Fiat-Shamir: from practice to theory (2019)
Canetti, R., Chen, Y., Reyzin, L., Rothblum, R.D.: Fiat-Shamir and correlation intractability from strong KDM-secure encryption. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 91–122. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_4
Canetti, R., Goldreich, O., Halevi, S.: The random oracle methodology, revisited. J. ACM 51(4), 557–594 (2004)
Chan, T.H., Chung, K., Lin, W., Shi, E.: MPC for MPC: secure computation on a massively parallel computing architecture. In: ITCS (2020)
Clear, M., McGoldrick, C.: Multi-identity and multi-key leveled FHE from learning with errors. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 630–656. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_31
Cohen, R., Shelat, A., Wichs, D.: Adaptively secure MPC with sublinear communication complexity. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11693, pp. 30–60. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_2
Dwork, C., Naor, M.: Zaps and their applications. SIAM J. Comput. 36(6), 1513–1543 (2007). https://doi.org/10.1137/S0097539703426817
Feige, U., Lapidot, D., Shamir, A.: Multiple noninteractive zero knowledge proofs under general assumptions. SIAM J. Comput. 29(1), 1–28 (1999)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Fitzi, M., Hirt, M., Maurer, U.: Trading correctness for privacy in unconditional multi-party computation. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 121–136. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055724
Fitzi, M., Hirt, M., Maurer, U.: General adversaries in unconditional multi-party computation. In: Lam, K.-Y., Okamoto, E., Xing, C. (eds.) ASIACRYPT 1999. LNCS, vol. 1716, pp. 232–246. Springer, Heidelberg (1999). https://doi.org/10.1007/978-3-540-48000-6_19
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: STOC, pp. 169–178 (2009)
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_5
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game. In: STOC, pp. 218–229. ACM (1987)
Dov Gordon, S., Liu, F.-H., Shi, E.: Constant-round MPC with fairness and guarantee of output delivery. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 63–82. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_4
Groth, J., Ostrovsky, R.: Cryptography in the multi-string model. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 323–341. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_18
Guo, Y., Pass, R., Shi, E.: Synchronous, with a chance of partition tolerance. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11692, pp. 499–529. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_18
Hirt, M., Maurer, U., Zikas, V.: MPC vs. SFE: unconditional and computational security. In: Pieprzyk, J. (ed.) ASIACRYPT 2008. LNCS, vol. 5350, pp. 1–18. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89255-7_1
Holmgren, J., Lombardi, A.: Cryptographic hashing from strong one-way functions (or: one-way product functions and their applications). In: FOCS (2018)
Jain, A., Rasmussen, P.M.R., Sahai, A.: Threshold fully homomorphic encryption. ePrint (2017). https://eprint.iacr.org/2017/257
Jain, A., Jin, Z.: Statistical zap arguments from quasi-polynomial LWE. IACR Crypt. ePrint Arch. 2019, 839 (2019)
Kalai, Y.T., Rothblum, G.N., Rothblum, R.D.: From obfuscation to the security of Fiat-Shamir for proofs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 224–251. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_8
López-Alt, A., Tromer, E., Vaikuntanathan, V.: On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption. In: STOC, pp. 1219–1234 (2012)
Mukherjee, P., Wichs, D.: Two round multiparty computation via multi-key FHE. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 735–763. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_26
Peikert, C., Shiehian, S.: Multi-key FHE from LWE, revisited. In: TCC Part II (2016)
Peikert, C., Shiehian, S.: Noninteractive zero knowledge for NP from (plain) learning with errors. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11692, pp. 89–114. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_4
Yao, A.C.: Protocols for secure computations. In: SFCS (1982)
Yao, A.C.C.: How to generate and exchange secrets (extended abstract). In: FOCS, pp. 162–167 (1986)
Acknowledgements
Saikrishna Badrinarayanan, Aayush Jain, Nathan Manohar, and Amit Sahai were supported in part from DARPA SAFEWARE and SIEVE awards, NTT Research, NSF Frontier Award 1413955, and NSF grant 1619348, BSF grant 2012378, a Xerox Faculty Research Award, a Google Faculty Research Award, an equipment grant from Intel, and an Okawa Foundation Research Grant. This material is based upon work supported by the Defense Advanced Research Projects Agency through Award HR00112020024 and the ARL under Contract W911NF-15-C- 0205. The views expressed are those of the authors and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, NTT Research, or the U.S. Government. Saikrishna Badrinarayanan was also partially supported by an IBM PhD fellowship. Aayush Jain was also partially supported by a Google PhD fellowship.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Badrinarayanan, S., Jain, A., Manohar, N., Sahai, A. (2020). Secure MPC: Laziness Leads to GOD. In: Moriai, S., Wang, H. (eds) Advances in Cryptology – ASIACRYPT 2020. ASIACRYPT 2020. Lecture Notes in Computer Science(), vol 12493. Springer, Cham. https://doi.org/10.1007/978-3-030-64840-4_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-64840-4_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64839-8
Online ISBN: 978-3-030-64840-4
eBook Packages: Computer ScienceComputer Science (R0)






 .
. by appropriately truncating or padding with 0’s if it was of incorrect length. Let
by appropriately truncating or padding with 0’s if it was of incorrect length. Let  . Let
. Let 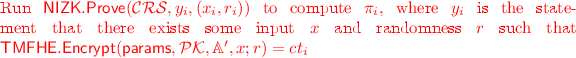 .
. .
. and
and
 Let
Let 
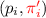 .
. and
and
 . Let
. Let 