Abstract
In this article we discuss classical theorems from Convex Geometry in the context of topological drawings. In a simple topological drawing of the complete graph \(K_n\), any two edges share at most one point: either a common vertex or a point where they cross. Triangles of simple topological drawings can be viewed as convex sets. This gives a link to convex geometry.
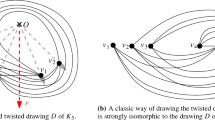
We present a generalization of Kirchberger’s Theorem, a family of simple topological drawings with arbitrarily large Helly number, and a new proof of a topological generalization of Carathéodory’s Theorem in the plane. We also discuss further classical theorems from Convex Geometry in the context of simple topological drawings.
We introduce “generalized signotopes” as a generalization of simple topological drawings. As indicated by the name they are a generalization of signotopes, a structure studied in the context of encodings for arrangements of pseudolines.
Raphael Steiner was funded by DFG-GRK 2434. Stefan Felsner and Manfred Scheucher were partially supported by DFG Grant FE 340/12-1. Manfred Scheucher was partially supported by the internal research funding “Post-Doc-Funding” from Technische Universität Berlin. We thank Alan Arroyo, Emo Welzl, Heiko Harborth, and Geza Tóth for helpful discussions. A special thanks goes to Patrick Schnider for his simplification of the construction in the proof of Proposition 3.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Arrangements of pseudolines obtained by such extensions are equivalent to pseudoconfigurations of points, and can be considered as oriented matroids of rank 3 (cf. Chapter 5.3 of [17]).
References
Aichholzer, O., Aurenhammer, F., Krasser, H.: Enumerating order types for small point sets with applications. Order 19(3), 265–281 (2002). https://doi.org/10.1023/A:1021231927255
Aichholzer, O., Hackl, T., Pilz, A., Salazar, G., Vogtenhuber, B.: Deciding monotonicity of good drawings of the complete graph. In: Proceedings of XVI Spanish Meeting on Computational Geometry (EGC 2015), pp. 33–36 (2015). http://www.ist.tugraz.at/cpgg/downloadables/ahpsv-dmgdc-15.pdf
Alon, N., Kleitman, D.J.: Piercing convex sets and the Hadwiger-Debrunner (\(p, q\))-problem. Adv. Math. 96(1), 103–112 (1992). https://doi.org/10.1016/0001-8708(92)90052-M
Arroyo, A., Bensmail, J., Richter, R.B.: Extending drawings of graphs to arrangements of pseudolines. In: 36th International Symposium on Computational Geometry (SoCG 2020). LIPIcs, vol. 164, pp. 9:1–9:14. Schloss Dagstuhl (2020). https://doi.org/10.4230/LIPIcs.SoCG.2020.9
Arroyo, A., McQuillan, D., Richter, R.B., Salazar, G.: Convex drawings of the complete graph: topology meets geometry (2017). arXiv:1712.06380
Arroyo, A., McQuillan, D., Richter, R.B., Salazar, G.: Drawings of \(K_n\) with the same rotation scheme are the same up to Reidemeister moves (Gioan’s Theorem). Aust. J. Comb. 67, 131–144 (2017). http://ajc.maths.uq.edu.au/pdf/67/ajcv67p131.pdf
Arroyo, A., McQuillan, D., Richter, R.B., Salazar, G.: Levi’s Lemma, pseudolinear drawings of \(K_n\), and empty triangles. J. Graph Theory 87(4), 443–459 (2018). https://doi.org/10.1002/jgt.22167
Arroyo, A., Richter, R.B., Sunohara, M.: Extending drawings of complete graphs into arrangements of pseudocircles (2020). arXiv:2001.06053
Bachem, A., Wanka, A.: Separation theorems for oriented matroids. Discret. Math. 70(3), 303–310 (1988). https://doi.org/10.1016/0012-365X(88)90006-4
Bachem, A., Wanka, A.: Euclidean intersection properties. J. Comb. Theory, Ser. B 47(1), 10–19 (1989). https://doi.org/10.1016/0095-8956(89)90061-0
Balko, M., Fulek, R., Kynčl, J.: Crossing numbers and combinatorial characterization of Monotone Drawings of \(K_n\). Discret. Comput. Geom. 53(1), 107–143 (2014). https://doi.org/10.1007/s00454-014-9644-z
Bárány, I., Shlosman, S.B., Szücs, A.: On a topological generalization of a theorem of Tverberg. J. Lond. Math. Soc. s2–23(1), 158–164 (1981). https://doi.org/10.1112/jlms/s2-23.1.158
Bárány, I.: A generalization of Carathéodory’s theorem. Discret. Math. 40(2), 141–152 (1982). https://doi.org/10.1016/0012-365X(82)90115-7
Bárány, I., Soberón, P.: Tverberg’s theorem is 50 years old: a survey. Bull. Amer. Math. Soc. 55, 459–492 (2018). https://doi.org/10.1090/bull/1634
Barvinok, A.: A Course in Convexity, Graduate Studies in Mathematics, vol. 54. American Mathematical Society (2002). https://doi.org/10.1090/gsm/054
Bergold, H., Felsner, S., Scheucher, M., Schröder, F., Steiner, R.: Topological Drawings meet Classical Theorems from Convex Geometry (2020). arXiv:2005.12568
Björner, A., Las Vergnas, M., White, N., Sturmfels, B., Ziegler, G.M.: Oriented Matroids, Encyclopedia of Mathematics and Its Applications, vol. 46. Cambridge University Press, 2 edn. (1999). https://doi.org/10.1017/CBO9780511586507
Chan, T.M., Har-Peled, S.: Approximation algorithms for maximum independent set of pseudo-disks. Discret. Comput. Geom. 48(2), 373–392 (2012). https://doi.org/10.1007/s00454-012-9417-5
Felsner, S., Weil, H.: Sweeps, arrangements and signotopes. Discret. Appl. Math. 109(1), 67–94 (2001). https://doi.org/10.1016/S0166-218X(00)00232-8
Frick, F., Soberón, P.: The topological Tverberg problem beyond prime powers (2020). arXiv:2005.05251
Gioan, E.: Complete graph drawings up to triangle mutations. In: Kratsch, D. (ed.) WG 2005. LNCS, vol. 3787, pp. 139–150. Springer, Heidelberg (2005). https://doi.org/10.1007/11604686_13
Goaoc, X., Paták, P., Patáková, Z., Tancer, M., Wagner, U.: Bounding Helly numbers via Betti numbers. In: Loebl, M., Nešetřil, J., Thomas, R. (eds.) A Journey Through Discrete Mathematics, pp. 407–447. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-44479-6_17
Goodman, J.E., Pollack, R.: Helly-type theorems for pseudoline arrangements in \(\cal{P}^2\). J. Comb. Theory Ser. A 32(1), 1–19 (1982). https://doi.org/10.1016/0097-3165(82)90061-9
Helly, E.: Über Systeme von abgeschlossenen Mengen mit gemeinschaftlichen Punkten. Monatshefte für Mathematik und Physik 37(1), 281–302 (1930). https://doi.org/10.1007/BF01696777
Holmsen, A.F.: The intersection of a matroid and an oriented matroid. Adv. Math. 290, 1–14 (2016). https://doi.org/10.1016/j.aim.2015.11.040
Holmsen, A.F., Pach, J., Tverberg, H.: Points surrounding the origin. Combinatorica 28(6), 633–644 (2008). https://doi.org/10.1007/s00493-008-2427-5
Kalai, G.: Colorful Caratheodory Revisited (2009). http://gilkalai.wordpress.com/2009/03/15/colorful-caratheodory-revisited
Kalai, G., Meshulam, R.: A topological colorful Helly theorem. Adv. Math. 191(2), 305–311 (2005). https://doi.org/10.1016/j.aim.2004.03.009
Keller, C., Smorodinsky, S., Tardos, G.: Improved bounds on the Hadwiger–Debrunner numbers. Isr. J. Math. 225(2), 925–945 (2018). https://doi.org/10.1007/s11856-018-1685-1
Kirchberger, P.: Über Tschebychefsche Annäherungsmethoden. Mathematische Annalen 57, 509–540 (1903)
Özaydin, M.: Equivariant maps for the symmetric group. Unpublished preprint, University of Wisconsin-Madison (1987). http://minds.wisconsin.edu/bitstream/handle/1793/63829/Ozaydin.pdf
Roudneff, J.P.: Tverberg-type theorems for pseudoconfigurations of points in the plane. Eur. J. Comb. 9(2), 189–198 (1988). https://doi.org/10.1016/S0195-6698(88)80046-5
Scheucher, M., Schrezenmaier, H., Steiner, R.: A note on universal point sets for planar graphs. J. Graph Algorithm. Appl. 24(3), 247–267 (2020). https://doi.org/10.7155/jgaa.00529
Scheucher, M.: Two disjoint 5-holes in point sets. Comput. Geom. Theory Appl. 91(101670) (2020). https://doi.org/10.1016/j.comgeo.2020.101670
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Bergold, H., Felsner, S., Scheucher, M., Schröder, F., Steiner, R. (2020). Topological Drawings Meet Classical Theorems from Convex Geometry. In: Auber, D., Valtr, P. (eds) Graph Drawing and Network Visualization. GD 2020. Lecture Notes in Computer Science(), vol 12590. Springer, Cham. https://doi.org/10.1007/978-3-030-68766-3_22
Download citation
DOI: https://doi.org/10.1007/978-3-030-68766-3_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-68765-6
Online ISBN: 978-3-030-68766-3
eBook Packages: Computer ScienceComputer Science (R0)