Abstract
The aim of this note is to give a construction and an enumeration of self-dual \(\theta \)-cyclic and \(\theta \)-negacyclic codes of length n over  where p is a prime number and \(\theta \) is the Frobenius automorphism over
where p is a prime number and \(\theta \) is the Frobenius automorphism over  . We use the notion of isodual codes to achieve this construction.
. We use the notion of isodual codes to achieve this construction.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Alahmadi, A., Alsulami, S., Hijazi, R., Solé, P.: Isodual cyclic codes over finite fields of odd characteristic. Discrete Math. 339(1), 344–353 (2016)
Batoul, A., Guenda, K., Gulliver, T.A.: Repeated-root isodual cyclic codes over finite fields. In: El Hajji, S., Nitaj, A., Carlet, C., Souidi, E.M. (eds.) C2SI 2015. LNCS, vol. 9084, pp. 119–132. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-18681-8_10
Batoul, A., Guenda, K., Kaya, A., Yildiz, B.: Cyclic isodual and formally self-dual codes over
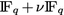 . Eur. J. Pure Appl. Math. 8(1), 64–80 (2015)
. Eur. J. Pure Appl. Math. 8(1), 64–80 (2015)Boucher, D.: A note on the existence of self-dual skew codes over finite fields. In: El Hajji, S., Nitaj, A., Carlet, C., Souidi, E.M. (eds.) C2SI 2015. LNCS, vol. 9084, pp. 228–239. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-18681-8_18
Boucher, D.: Construction and number of self-dual skew codes over
 . Adv. Math. Commun. 10(4), 765–795 (2016)
. Adv. Math. Commun. 10(4), 765–795 (2016)Boucher, D.: Autour de codes définis à l’aide de polynômes tordus. Habilitation à diriger des recherches de l’Université Rennes 1, 2 juin 2020
Boucher, D., Ulmer, F.: Codes as modules over skew polynomial rings. In: Parker, M.G. (ed.) IMACC 2009. LNCS, vol. 5921, pp. 38–55. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10868-6_3
Boucher, D., Ulmer, F.: A note on the dual codes of module skew codes. In: Chen, L. (ed.) IMACC 2011. LNCS, vol. 7089, pp. 230–243. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25516-8_14
Boucher, D., Ulmer, F.: Linear codes using skew polynomials with automorphisms and derivations. Des. Codes Cryptogr. 70(3), 405–431 (2012). https://doi.org/10.1007/s10623-012-9704-4
Caruso, X., Le Borgne, J.: A new faster algorithm for factoring skew polynomials over finite fields. J. Symbolic Comput. 79(part 2), 411–443 (2017)
Delenclos, J., Leroy, A.: Noncommutative symmetric functions and \(W\)-polynomials. J. Algebra Appl. 6(5), 815–837 (2007)
Gabidulin, È.M.: Theory of codes with maximum rank distance. Problemy Peredachi Informatsii 21(1), 3–16 (1985)
Jacobson, N.: The Theory of Rings. American Mathematical Society Mathematical Surveys, vol. II. American Mathematical Society, New York (1943)
Lam, T.Y., Leroy, A.: Vandermonde and Wronskian matrices over division rings. Bull. Soc. Math. Belg. Sér. A 40(2), 281–286 (1988). Deuxième Contact Franco-Belge en Algèbre (Faulx-les-Tombes, 1987)
Nebe, G., Willems, W.: On self-dual MRD codes. Adv. Math. Commun. 10(3), 633–642 (2016)
Ore, O.: Theory of Non-commutative Polynomials. Ann. Math. 34(3), 480–508 (1933)
Rains, E.M., Sloane, N.J.A.: Self-dual codes. In: Handbook of Coding Theory, vol. I, II, pp. 177–294. North-Holland, Amsterdam (1998)
Acknowledgments
The authors thank the referees for their fruitful remarks. The second author is supported by the French government “Investissements d’Avenir” program ANR-11-LABX-0020-01.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
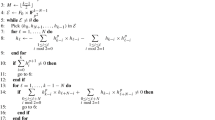
Batoul, A., Boucher, D., Boulanouar, R.D. (2021). A Construction of Self-dual Skew Cyclic and Negacyclic Codes of Length n over  .
In: Bajard, J.C., Topuzoğlu, A. (eds) Arithmetic of Finite Fields. WAIFI 2020. Lecture Notes in Computer Science(), vol 12542. Springer, Cham. https://doi.org/10.1007/978-3-030-68869-1_6
.
In: Bajard, J.C., Topuzoğlu, A. (eds) Arithmetic of Finite Fields. WAIFI 2020. Lecture Notes in Computer Science(), vol 12542. Springer, Cham. https://doi.org/10.1007/978-3-030-68869-1_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-68869-1_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-68868-4
Online ISBN: 978-3-030-68869-1
eBook Packages: Computer ScienceComputer Science (R0)



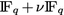 . Eur. J. Pure Appl. Math. 8(1), 64–80 (2015)
. Eur. J. Pure Appl. Math. 8(1), 64–80 (2015) . Adv. Math. Commun. 10(4), 765–795 (2016)
. Adv. Math. Commun. 10(4), 765–795 (2016)