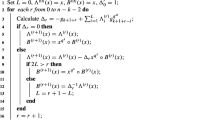Skip to main content
Springer Nature Link
Log in

Decoding up to 4 Errors in Hyperbolic-Like Abelian Codes by the Sakata Algorithm

  • Conference paper
  • First Online:
Arithmetic of Finite Fields (WAIFI 2020)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 12542))

Included in the following conference series:

  • 634 Accesses

Abstract

We deal with two problems related with the use of the Sakata’s algorithm in a specific class of bivariate codes (see [2, 8, 9]). The first one is to improve the general framework of locator decoding in order to apply it on such abelian codes. The second one is to find sufficient conditions to guarantee that the minimal set of polynomials given by the algorithm is exactly a Groebner basis of the locator ideal.

This work was partially supported by MINECO, project MTM2016-77445-P, and Fundación Séneca of Murcia, project 19880/GERM/15.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Bernal, J.J., Bueno-Carreño, D.H., Simón, J.J.: Apparent distance and a notion of BCH multivariate codes. IEEE Trans. Inf. Theory 62(2), 655–668 (2016)

    Article  MathSciNet  Google Scholar 

  2. Blahut, R.E.: Decoding of cyclic codes and codes on curves. In: Huffman, W.C., Pless, V. (eds.) Handbook of Coding Theory, vol. II, pp. 1569–1633 (1998)

    Google Scholar 

  3. Camion, P.: Abelian codes. MCR Tech. Sum. Rep. 1059, University of Wisconsin, Madison (1970)

    Google Scholar 

  4. Cox, D.A., Little, J., O’Shea, D.: Ideals, Varieties, and Algorithms. Springer, Heidelberg (1998). https://doi.org/10.1007/978-3-662-41154-4

    Book  MATH  Google Scholar 

  5. Hackl, M.: Multivariate polynomial codes. Johannes-Kepler-University (2000)

    Google Scholar 

  6. Imai, H.: A theory of two-dimensional cyclic codes. Inf. Control 34(1), 1–21 (1977)

    Article  MathSciNet  Google Scholar 

  7. Rubio, I.M., Sweedler, M., Heegard, C.: Finding a Gröbner basis for the ideal of recurrence relations on m-dimensional periodic arrays. In: 12th International Conference on Finite Fields and Their Applications, Contemporary Developments in Finite Fields and Applications, pp. 296–320. World Scientific (2016)

    Google Scholar 

  8. Sakata, S.: Finding a minimal set of linear recurring relations capable of generating a given finite two-dimensional array. J. Symb. Comput. 5, 321–337 (1988)

    Article  MathSciNet  Google Scholar 

  9. Sakata, S.: Decoding binary cyclic 2-D codes by the 2-D Berlekamp-Massey algorithm. IEEE Trans. Inf. Theory 37(4), 1200–1203 (1991)

    Article  MathSciNet  Google Scholar 

  10. Sakata, S.: The BMS algorithm and decoding of AG codes. In: Sala, M., Sakata, S., Mora, T., Traverso, C., Perret, L. (eds.) Gröbner Basis, Coding, and Cryptography, pp. 165–185. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-540-93806-4_10

    Chapter  Google Scholar 

  11. Sakata, S.: The BMS Algorithm. In: Sala, M., Sakata, S., Mora, T., Traverso, C., Perret, L. (eds.) Gröbner Basis, Coding, and Cryptography, pp. 143–163. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-540-93806-4_9

    Chapter  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Departamento de Matemáticas, Universidad de Murcia, 30100, Murcia, Spain

    José Joaquín Bernal & Juan Jacobo Simón

Authors
  1. José Joaquín Bernal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Juan Jacobo Simón
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Juan Jacobo Simón .

Editor information

Editors and Affiliations

  1. Sorbonne Paris, Paris, France

    Jean Claude Bajard

  2. Sabancı University, Istanbul, Turkey

    Alev Topuzoğlu

Rights and permissions

Reprints and permissions

Copyright information

© 2021 Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Bernal, J.J., Simón, J.J. (2021). Decoding up to 4 Errors in Hyperbolic-Like Abelian Codes by the Sakata Algorithm. In: Bajard, J.C., Topuzoğlu, A. (eds) Arithmetic of Finite Fields. WAIFI 2020. Lecture Notes in Computer Science(), vol 12542. Springer, Cham. https://doi.org/10.1007/978-3-030-68869-1_7

Download citation

  • DOI: https://doi.org/10.1007/978-3-030-68869-1_7

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-030-68868-4

  • Online ISBN: 978-3-030-68869-1

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics