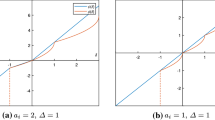
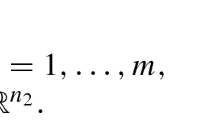Abstract
The goal of this paper is to derive new classes of valid convex inequalities for quadratically constrained quadratic programs (QCQPs) through the technique of lifting. Our first main result shows that, for sets described by one bipartite bilinear constraint together with bounds, it is always possible to lift a seed inequality that is valid for a restriction obtained by fixing variables to their bounds, when the lifting is accomplished using affine functions of the fixed variables. In this setting, sequential lifting involves solving a non-convex nonlinear optimization problem each time a variable is lifted, just as in Mixed Integer Linear Programming. To reduce the computational burden associated with this procedure, we develop a framework based on subadditive approximations of lifting functions that permits sequence independent lifting of seed inequalities for separable bipartite bilinear sets. In particular, this framework permits the derivation of closed-form valid inequalities. We then study a separable bipartite bilinear set where the coefficients form a minimal cover with respect to right-hand-side. For this set, we derive a “bilinear cover inequality”, which is second-order cone representable. We argue that this bilinear covering inequality is strong by showing that it yields a constant-factor approximation of the convex hull of the original set. We study its lifting function and construct a two-slope subadditive upper bound. Using this subadditive approximation, we lift fixed variable pairs in closed-form, thus deriving a “lifted bilinear cover inequality” that is valid for general separable bipartite bilinear sets with box constraints.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
We use the term bipartite, perhaps redundantly, to highlight that variables can be divided into two groups, such that any degree two term comes from product of variables one each from these two groups [22].
- 2.
We say “almost”, since there are non-packing examples, such as \(S:= \{x,y \in [0, 1]^2\,|\, x_1y_1 - 100x_2y_2 \ge -98\}\), where there is no partition that yields a minimal cover. Such sets are “overwhelmingly” like a packing set; in the case of the example, it is a perturbation of the packing set \(\{x_2, y_2 \in [0, 1]\,|\, 100x_2y_2\le 98\}\). For such sets it is not difficult to show that \(conv (S)\) is polyhedral.
References
Agra, A., Constantino, M.F.: Lifting two-integer knapsack inequalities. Math. Program. 109(1), 115–154 (2007). https://doi.org/10.1007/s10107-006-0705-9
Anstreicher, K.M., Burer, S., Park, K.: Convex hull representations for bounded products of variables. arXiv preprint arXiv:2004.07233 (2020)
Atamtürk, A.: On the facets of the mixed-integer knapsack polyhedron. Math. Program. 98(1), 145–175 (2003). https://doi.org/10.1007/s10107-003-0400-z
Atamtürk, A.: Sequence independent lifting for mixed-integer programming. Oper. Res. 52(3), 487–490 (2004)
Atamtürk, A., Narayanan, V.: Lifting for conic mixed-integer programming. Math. Program. 126(2), 351–363 (2011). https://doi.org/10.1007/s10107-009-0282-9
Averkov, G., Basu, A.: Lifting properties of maximal lattice-free polyhedra. Math. Program. 154(1–2), 81–111 (2015). https://doi.org/10.1007/s10107-015-0865-6
Balas, E.: Facets of the knapsack polytope. Math. Program. 8(1), 146–164 (1975). https://doi.org/10.1007/BF01580440
Balas, E.: Disjunctive programming: properties of the convex hull of feasible points. Discrete Appl. Math. 89(1–3), 3–44 (1998)
Balas, E., Jeroslow, R.G.: Strengthening cuts for mixed integer programs. Eur. J. Oper. Res. 4(4), 224–234 (1980)
Balas, E., Zemel, E.: Facets of the knapsack polytope from minimal covers. SIAM J. Appl. Math. 34(1), 119–148 (1978)
Basu, A., Campêlo, M., Conforti, M., Cornuéjols, G., Zambelli, G.: Unique lifting of integer variables in minimal inequalities. Math. Program. 141(1–2), 561–576 (2013). https://doi.org/10.1007/s10107-012-0560-9
Basu, A., Cornuéjols, G., Köppe, M.: Unique minimal liftings for simplicial polytopes. Math. Oper. Res. 37(2), 346–355 (2012)
Basu, A., Dey, S.S., Paat, J.: Nonunique lifting of integer variables in minimal inequalities. SIAM J. Discrete Math. 33(2), 755–783 (2019)
Basu, A., Paat, J.: Operations that preserve the covering property of the lifting region. SIAM J. Optim. 25(4), 2313–2333 (2015)
Ben-Tal, A., Nemirovski, A.: Lectures on modern convex optimization: analysis, algorithms, and engineering applications. SIAM (2001)
Bienstock, D., Chen, C., Munoz, G.: Outer-product-free sets for polynomial optimization and oracle-based cuts. Math. Program. 183, 1–44 (2020). https://doi.org/10.1007/s10107-020-01484-3
Burer, S.: A gentle, geometric introduction to copositive optimization. Math. Program. 151(1), 89–116 (2015). https://doi.org/10.1007/s10107-015-0888-z
Ceria, S., Cordier, C., Marchand, H., Wolsey, L.A.: Cutting planes for integer programs with general integer variables. Math. Program. 81(2), 201–214 (1998). https://doi.org/10.1007/BF01581105
Chung, K., Richard, J.P.P., Tawarmalani, M.: Lifted inequalities for 0–1 mixed-integer bilinear covering sets. Math. Program. 145(1–2), 403–450 (2014). https://doi.org/10.1007/s10107-013-0652-1
Conforti, M., Cornuéjols, G., Zambelli, G.: A geometric perspective on lifting. Oper. Res. 59(3), 569–577 (2011)
Dey, S.S., Richard, J.P.P.: Linear-programming-based lifting and its application to primal cutting-plane algorithms. INFORMS J. Comput. 21(1), 137–150 (2009)
Dey, S.S., Santana, A., Wang, Y.: New SOCP relaxation and branching rule for bipartite bilinear programs. Optim. Eng. 20(2), 307–336 (2019)
Dey, S.S., Wolsey, L.A.: Composite lifting of group inequalities and an application to two-row mixing inequalities. Discrete Optim. 7(4), 256–268 (2010)
Dey, S.S., Wolsey, L.A.: Constrained infinite group relaxations of MIPs. SIAM J. Optim. 20(6), 2890–2912 (2010)
Dey, S.S., Wolsey, L.A.: Two row mixed-integer cuts via lifting. Math. Program. 124(1–2), 143–174 (2010). https://doi.org/10.1007/s10107-010-0362-x
Espinoza, D., Fukasawa, R., Goycoolea, M.: Lifting, tilting and fractional programming revisited. Oper. Res. Lett. 38(6), 559–563 (2010)
Gómez, A.: Submodularity and valid inequalities in nonlinear optimization with indicator variables (2018)
Gomory, R.E., Johnson, E.L.: Some continuous functions related to corner polyhedra. Math. Program. 3(1), 23–85 (1972). https://doi.org/10.1007/BF01584976
Gu, Z., Nemhauser, G.L., Savelsbergh, M.W.P.: Lifted flow cover inequalities for mixed 0–1 integer programs. Math. Program. 85(3), 439–467 (1999). https://doi.org/10.1007/s101070050067
Gu, Z., Nemhauser, G.L., Savelsbergh, M.W.P.: Sequence independent lifting in mixed integer programming. J. Comb. Optim. 4(1), 109–129 (2000)
Günlük, O., Pochet, Y.: Mixing mixed-integer inequalities. Math. Program. 90(3), 429–457 (2001). https://doi.org/10.1007/PL00011430
Gupte, A.: Mixed integer bilinear programming with applications to the pooling problem. Ph.D. thesis, Georgia Institute of Technology (2012)
Hammer, P.L., Johnson, E.L., Peled, U.N.: Facet of regular 0–1 polytopes. Math. Program. 8(1), 179–206 (1975). https://doi.org/10.1007/BF01580442
Kaparis, K., Letchford, A.N.: Local and global lifted cover inequalities for the 0–1 multidimensional knapsack problem. Eur. J. Oper. Res. 186(1), 91–103 (2008)
Köppe, M., Zhou, Y.: An electronic compendium of extreme functions for the Gomory-Johnson infinite group problem. Oper. Res. Lett. 43(4), 438–444 (2015)
Martin, A., Weismantel, R.: The intersection of knapsack polyhedra and extensions. In: Bixby, R.E., Boyd, E.A., Ríos-Mercado, R.Z. (eds.) IPCO 1998. LNCS, vol. 1412, pp. 243–256. Springer, Heidelberg (1998). https://doi.org/10.1007/3-540-69346-7_19
McCormick, G.P.: Computability of global solutions to factorable nonconvex programs: part I - convex underestimating problems. Math. Program. 10(1), 147–175 (1976). https://doi.org/10.1007/BF01580665
Muñoz, G., Serrano, F.: Maximal quadratic-free sets. In: Bienstock, D., Zambelli, G. (eds.) IPCO 2020. LNCS, vol. 12125, pp. 307–321. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45771-6_24
Narisetty, A.K., Richard, J.P.P., Nemhauser, G.L.: Lifted tableaux inequalities for 0–1 mixed-integer programs: a computational study. INFORMS J. Comput. 23(3), 416–424 (2011)
Nguyen, T.T., Richard, J.P.P., Tawarmalani, M.: Deriving convex hulls through lifting and projection. Math. Program. 169(2), 377–415 (2018). https://doi.org/10.1007/s10107-017-1138-3
Padberg, M.W.: On the facial structure of set packing polyhedra. Math. Program. 5(1), 199–215 (1973). https://doi.org/10.1007/BF01580121
Padberg, M.W.: A note on zero-one programming. Oper. Res. 23(4), 833–837 (1975)
Rahman, H., Mahajan, A.: Facets of a mixed-integer bilinear covering set with bounds on variables. J. Global Optim. 74(3), 417–442 (2019)
Richard, J.P.P.: Lifting techniques for mixed integer programming. In: Wiley Encyclopedia of Operations Research and Management Science (2010)
Richard, J.-P.P., Dey, S.S.: The group-theoretic approach in mixed integer programming. In: Jünger, M., et al. (eds.) 50 Years of Integer Programming 1958-2008, pp. 727–801. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-540-68279-0_19
Richard, J.P.P., de Farias Jr, I.R., Nemhauser, G.L.: Lifted inequalities for 0–1 mixed integer programming: basic theory and algorithms. Math. Program. 98(1–3), 89–113 (2003). https://doi.org/10.1007/s10107-003-0398-2
Richard, J.P.P., de Farias Jr, I.R., Nemhauser, G.L.: Lifted inequalities for 0–1 mixed integer programming: superlinear lifting. Math. Program. 98(1–3), 115–143 (2003). https://doi.org/10.1007/s10107-003-0399-1
Richard, J.P.P., Li, Y., Miller, L.A.: Valid inequalities for MIPs and group polyhedra from approximate liftings. Math. Program. 118(2), 253–277 (2009). https://doi.org/10.1007/s10107-007-0190-9
Richard, J.P.P., Tawarmalani, M.: Lifting inequalities: a framework for generating strong cuts for nonlinear programs. Math. Program. 121(1), 61–104 (2010). https://doi.org/10.1007/s10107-008-0226-9
Santana, A., Dey, S.S.: The convex hull of a quadratic constraint over a polytope. SIAM J. Optim. 30(4), 2983–2997 (2020)
Tawarmalani, M., Richard, J.P.P., Chung, K.: Strong valid inequalities for orthogonal disjunctions and bilinear covering sets. Math. Program. 124(1–2), 481–512 (2010). https://doi.org/10.1007/s10107-010-0374-6
Wolsey, L.A.: Facets and strong valid inequalities for integer programs. Oper. Res. 24(2), 367–372 (1976)
Wolsey, L.A.: Valid inequalities and superadditivity for 0–1 integer programs. Math. Oper. Res. 2(1), 66–77 (1977)
Zeng, B., Richard, J.-P.P.: A framework to derive multidimensional superadditive lifting functions and its applications. In: Fischetti, M., Williamson, D.P. (eds.) IPCO 2007. LNCS, vol. 4513, pp. 210–224. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72792-7_17
Zeng, B., Richard, J.P.P.: A polyhedral study on 0–1 knapsack problems with disjoint cardinality constraints: facet-defining inequalities by sequential lifting. Discrete Optim. 8(2), 277–301 (2011)
Zeng, B., Richard, J.P.P.: A polyhedral study on 0–1 knapsack problems with disjoint cardinality constraints: strong valid inequalities by sequence-independent lifting. Discrete Optim. 8(2), 259–276 (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Gu, X., Dey, S.S., Richard, JP.P. (2021). Lifting Convex Inequalities for Bipartite Bilinear Programs. In: Singh, M., Williamson, D.P. (eds) Integer Programming and Combinatorial Optimization. IPCO 2021. Lecture Notes in Computer Science(), vol 12707. Springer, Cham. https://doi.org/10.1007/978-3-030-73879-2_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-73879-2_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-73878-5
Online ISBN: 978-3-030-73879-2
eBook Packages: Computer ScienceComputer Science (R0)