Abstract
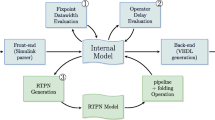
This paper introduces an extension of Timed Petri Nets for the modeling of synchronous electronic circuits, addressing pipeline design problems. Petri Nets have been widely used for the modeling of electronic circuits. In particular, Timed Petri Nets which capture timing properties are perfectly suited for scheduling problems. Our extension, through reset that model the pipeline stages, and through delayable transitions that relax timing constraints, allows to widen the conception space of pipelined systems.
After discussing about maximal-step firing rule and the semantics of Timed Petri Nets “à la Ramchandani”, we define our Timed Petri Nets with reset and delayable (non-asap) transitions.
We then study the decidability and the complexity of the main problems of interest. We propose an abstraction of the state space. We then establish a translation of this model into a single-clock timed automata, which preserves the language. This translation settles the decidability on language inclusion and universality problems.
Finally, an algorithm for the exploration of the state space is provided, and can be driven by the optimisation of various properties of the pipeline.
This work is supported by the Renault-Centrale Nantes chair dedicated to the propulsion performance of electric vehicles.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
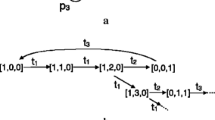
For the sake of brevity, in all the following figures, we note a marking M as a set of marked places instead of a vector and we give the valuation v only for the enabled transitions.
References
Abdulla, P.A., Deneux, J., Ouaknine, J., Quaas, K., Worrell, J.: Universality analysis for one-clock timed automata. Fundam. Informaticae 89(4), 419–450 (2008)
Alur, R., Courcoubetis, C., Dill, D.: Model-checking in dense real-time. Inf. Comput. 104(1), 2–34 (1993)
Alur, R., Dill, D.L.: A theory of timed automata. Theoret. Comput. Sci. 126(2), 183–235 (1994)
Bérard, B., Cassez, F., Haddad, S., Lime, D., Roux, O.H.: The expressive power of time Petri nets. Theoretical Comput. Sci. (TCS) 474, 1–20 (2013)
Boucheneb, H., Gardey, G., Roux, O.H.: TCTL model checking of time Petri nets. J. Log. Comput. 19(6), 1509–1540 (2009)
Bufistov, D., Cortadella, J., Kishinevsky, M., Sapatnekar, S.: A general model for performance optimization of sequential systems. In: 2007 IEEE/ACM International Conference on Computer-Aided Design, pp. 362–369 (2007)
Campos, J., Chiola, G., Colom, J.M., Silva, M.: Properties and performance bounds for timed marked graphs. IEEE Trans. Circuits Syst. I: Fund. Theory Appl. 39(5), 386–401 (1992)
Carloni, L.P., McMillan, K.L., Saldanha, A., Sangiovanni-Vincentelli, A.L.: A methodology for correct-by-construction latency insensitive design. In: 1999 IEEE/ACM International Conference on Computer-Aided Design. Digest of Technical Papers (Cat. No.99CH37051), pp. 309–315 (1999)
Cassez, F., Roux, O.H.: Structural translation from Time Petri Nets to Timed Automata - Model-Checking Time Petri Nets via Timed Automata. J. Syst. Softw. 79(10), 1456–1468 (2006)
Cheng, A., Esparza, J., Palsberg, J.: Complexity results for 1-safe nets. Theoret. Comput. Sci. 147, 117–136 (1995)
Church, A.: Application of recursive arithmetic to the problem of circuit synthesis, pp. 3–50 (1957)
Giua, A., DiCesare, F., Silva, M.: Generalized mutual exclusion constraints on nets with uncontrollable transitions. In: IEEE International Conference on SMC (1992)
Istoan, M., de Dinechin, F.: Automating the pipeline of arithmetic datapaths. In: Design, Automation & Test in Europe Conference & Exhibition (DATE 2017), pp. 704–709, Lausanne, Switzerland (2017)
Josipović, L., Sheikhha, S., Guerrieri, A., Ienne, P., Cortadella, J.: Buffer placement and sizing for high-performance dataflow circuits. In: Proceedings of the 2020 ACM/SIGDA Int. Symposium on Field-Programmable Gate Arrays, FPGA 2020, pp. 186–196. Association for Computing Machinery, New York (2020)
Leiserson, C.E., Saxe, J.B.: Retiming synchronous circuitry. Algorithmica 6(1–6), 5–35 (1991)
Merlin, P.M.: A study of the recoverability of computing systems. Ph.D. thesis, Dep. of Information and Computer Science, University of California, Irvine, CA (1974)
Najibi, M., Beerel, P.A.: Slack matching mode-based asynchronous circuits for average-case performance. In: Proceedings of the International Conference on Computer-Aided Design, ICCAD 2013, pp. 219–225. IEEE Press (2013)
Ouaknine, J., Worrell, J.: On the language inclusion problem for timed automata: closing a decidability gap. In: Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science, 2004, pp. 54–63 (2004)
Popova-Zeugmann, L.: Time and Petri Nets. Springer (2013)
Ramchandani, C.: Analysis of asynchronous concurrent systems by timed Petri nets. Ph.D. thesis, Massachusetts Institute of Technology, Cambridge, MA (1974)
Kim, S., Beerel, P.A.: Pipeline optimization for asynchronous circuits: complexity analysis and an efficient optimal algorithm. IEEE Trans. Comput.-Aided Des. Integrated Circuits Syst. 25(3), 389–4022 (2006)
Zuberek, W.: D-timed petri nets and modeling of timeouts and protocols. Trans. Soc. Comput. Simul. 4(4), 331–357 (1987)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Parrot, R., Briday, M., Roux, O.H. (2021). Timed Petri Nets with Reset for Pipelined Synchronous Circuit Design. In: Buchs, D., Carmona, J. (eds) Application and Theory of Petri Nets and Concurrency. PETRI NETS 2021. Lecture Notes in Computer Science(), vol 12734. Springer, Cham. https://doi.org/10.1007/978-3-030-76983-3_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-76983-3_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-76982-6
Online ISBN: 978-3-030-76983-3
eBook Packages: Computer ScienceComputer Science (R0)