Skip to main content
Springer Nature Link
Log in

A Multidimensional Item Response Theory Model for Rubric-Based Writing Assessment

  • Conference paper
  • First Online:
Artificial Intelligence in Education (AIED 2021)

Part of the book series: Lecture Notes in Computer Science ((LNAI,volume 12748))

Included in the following conference series:

  • 3568 Accesses

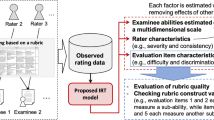
Abstract

When human raters grade student writing assignments, writing assessment often involves the use of a scoring rubric consisting of multiple evaluation items in order to increase the objectivity of evaluation. However, even when using a rubric, assigned scores are known to be influenced by the characteristics of both the rubric’s evaluation items and the raters, thus decreasing the reliability of student assessment. To resolve this problem, these characteristic effects have been considered in many recently proposed item response theory (IRT) models for estimating student ability. Such IRT models assume unidimensionality, meaning that a rubric measures one latent ability; in practice, however, this assumption might not be satisfied because a rubric’s evaluation items are often designed to measure multiple sub-abilities that constitute a targeted ability. To address this issue, this study proposes a multidimensional extension of such an IRT model for rubric-based writing assessment. The proposed model improves the assessment reliability. Furthermore, the model is useful for objective and detailed analysis of rubric quality and its construct validity. This study demonstrates the effectiveness of the proposed model through simulation experiments and application to real data.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Abosalem, Y.: Beyond translation: adapting a performance-task-based assessment of critical thinking ability for use in Rwanda. Int. J. Second. Educ. 4(1), 1–11 (2016)

    Article  Google Scholar 

  2. Bernardin, H.J., Thomason, S., Buckley, M.R., Kane, J.S.: Rater rating-level bias and accuracy in performance appraisals: the impact of rater personality, performance management competence, and rater accountability. Hum. Resour. Manag. 55(2), 321–340 (2016)

    Article  Google Scholar 

  3. Brooks, S., Gelman, A., Jones, G., Meng, X.: Handbook of Markov Chain Monte Carlo. Chapman & Hall/ CRC Handbooks of Modern Statistical Methods, CRC Press, Boca Raton (2011)

    Book  MATH  Google Scholar 

  4. Carpenter, B., Gelman, A., Hoffman, M., Lee, D., Goodrich, B., Betancourt, M., Brubaker, M., Guo, J., Li, P., Riddell, A.: Stan: a probabilistic programming language. J. Stat. Softw. Art. 76(1), 1–32 (2017)

    Google Scholar 

  5. Chan, S., Bax, S., Weir, C.: Researching participants taking IELTS Academic Writing Task 2 (AWT2) in paper mode and in computer mode in terms of score equivalence, cognitive validity and other factors. Technical report, IELTS Research Reports Online Series (2017)

    Google Scholar 

  6. Deng, S., McCarthy, D.E., Piper, M.E., Baker, T.B., Bolt, D.M.: Extreme response style and the measurement of intra-individual variability in affect. Multivar. Behav. Res. 53(2), 199–218 (2018)

    Article  Google Scholar 

  7. Eckes, T.: Introduction to Many-Facet Rasch Measurement: Analyzing and Evaluating Rater-Mediated Assessments. Peter Lang Pub. Inc., New York (2015)

    Google Scholar 

  8. Fox, J.P.: Bayesian Item Response Modeling: Theory and applications. Springer, Heidelberg (2010)

    Google Scholar 

  9. Gelman, A., Carlin, J., Stern, H., Dunson, D., Vehtari, A., Rubin, D.: Bayesian Data Analysis, Third Edition. Chapman & Hall/CRC Texts in Statistical Science, Taylor & Francis, London (2013)

    Google Scholar 

  10. Gelman, A., Rubin, D.B.: Inference from iterative simulation using multiple sequences. Stat. Sci. 7(4), 457–472 (1992)

    MATH  Google Scholar 

  11. Hoffman, M.D., Gelman, A.: The No-U-Turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 15, 1593–1623 (2014)

    MathSciNet  MATH  Google Scholar 

  12. Hua, C., Wind, S.A.: Exploring the psychometric properties of the mind-map scoring rubric. Behaviormetrika 46(1), 73–99 (2019)

    Article  Google Scholar 

  13. Hussein, M.A., Hassan, H.A., Nassef, M.: Automated language essay scoring systems: a literature review. PeerJ Comput. Sci. 5, e208 (2019)

    Google Scholar 

  14. Hutten, L.R.: Some Empirical Evidence for Latent Trait Model Selection. ERIC Clearinghouse (1980)

    Google Scholar 

  15. Jin, K.Y., Wang, W.C.: A new facets model for rater’s centrality/extremity response style. J. Educ. Meas. 55(4), 543–563 (2018)

    Article  Google Scholar 

  16. Kaliski, P.K., Wind, S.A., Engelhard, G., Morgan, D.L., Plake, B.S., Reshetar, R.A.: Using the many-faceted Rasch model to evaluate standard setting judgments. Educ. Psychol. Measur. 73(3), 386–411 (2013)

    Article  Google Scholar 

  17. Kose, I.A., Demirtasli, N.C.: Comparison of unidimensional and multidimensional models based on item response theory in terms of both variables of test length and sample size. Procedia. Soc. Behav. Sci. 46, 135–140 (2012)

    Article  Google Scholar 

  18. Linacre, J.M.: Many-faceted Rasch Measurement. MESA Press, San Diego (1989)

    Google Scholar 

  19. Linlin, C.: Comparison of automatic and expert teachers’ rating of computerized English listening-speaking test. Engl. Lang. Teach. 13(1), 18 (2019)

    Article  Google Scholar 

  20. Liu, O.L., Frankel, L., Roohr, K.C.: Assessing critical thinking in higher education: current state and directions for next-generation assessment. ETS Res. Rep. Ser. 1, 1–23 (2014)

    Google Scholar 

  21. Lord, F.: Applications of item response theory to practical testing problems. Erlbaum Associates, Mahwah (1980)

    Google Scholar 

  22. Martin-Fernandez, M., Revuelta, J.: Bayesian estimation of multidimensional item response models. a comparison of analytic and simulation algorithms. Int. J. Methodol. Exp. Psychol.38(1), 25–55 (2017)

    Google Scholar 

  23. Matsushita, K., Ono, K., Takahashi, Y.: Development of a rubric for writing assessment and examination of its reliability [in Japanese]. J. Lib. Gen. Educ. Soc. Japan 35(1), 107–115 (2013)

    Google Scholar 

  24. Muraki, E.: A generalized partial credit model. In: van der Linden, W.J., Hambleton, R.K. (eds.) Handbook of Modern Item Response Theory, pp. 153–164. Springer (1997)

    Google Scholar 

  25. Myford, C.M., Wolfe, E.W.: Detecting and measuring rater effects using many-facet Rasch measurement: part I. J. Appl. Meas. 4, 386–422 (2003)

    Google Scholar 

  26. Nakajima, A.: Achievements and issues in the application of rubrics in academic writing: a case study of the college of images arts and sciences [in Japanese]. Ritsumeikan High. Educ. Stud. 17, 199–215 (2017)

    Google Scholar 

  27. Nguyen, T., Uto, M., Abe, Y., Ueno, M.: Reliable peer assessment for team project based learning using item response theory. In: Proceedings of the International Conference on Computers in Education, pp. 144–153 (2015)

    Google Scholar 

  28. Patz, R.J., Junker, B.W., Johnson, M.S., Mariano, L.T.: The hierarchical rater model for rated test items and its application to large-scale educational assessment data. J. Educ. Behav. Stat. 27(4), 341–384 (2002)

    Article  Google Scholar 

  29. Patz, R.J., Junker, B.: Applications and extensions of MCMC in IRT: multiple item types, missing data, and rated responses. J. Educ. Behav. Stat. 24(4), 342–366 (1999)

    Article  Google Scholar 

  30. Rahman, A.A., Hanafi, N.M., Yusof, Y., Mukhtar, M.I., Yusof, A.M., Awang, H.: The effect of rubric on rater’s severity and bias in TVET laboratory practice assessment: analysis using many-facet Rasch measurement. J. Tech. Educ. Train. 12(1), 57–67 (2020)

    Google Scholar 

  31. Reckase, M.D.: Multidimensional Item Response Theory Models. Springer, New York (2009). https://doi.org/10.1007/978-0-387-89976-3_4

  32. Rosen, Y., Tager, M.: Making student thinking visible through a concept map in computer-based assessment of critical thinking. J. Educ. Comput. Res. 50(2), 249–270 (2014)

    Article  Google Scholar 

  33. Samejima, F.: Estimation of latent ability using a response pattern of graded scores. Psychometrika Monogr. 17, 1–100 (1969)

    Google Scholar 

  34. Schendel, R., Tolmie, A.: Assessment techniques and students’ higher-order thinking skills. Assess. Eval. High. Educ. 42(5), 673–689 (2017)

    Article  Google Scholar 

  35. Shin, H.J., Rabe-Hesketh, S., Wilson, M.: Trifactor models for multiple-ratings data. Multivar. Behav. Res. 54(3), 360–381 (2019)

    Article  Google Scholar 

  36. Soo Park, Y., Xing, K.: Rater model using signal detection theory for latent differential rater functioning. Multivar. Behav. Res. 54(4), 492–504 (2019)

    Article  Google Scholar 

  37. Stan Development Team: RStan: the R interface to stan. R package version 2.17.3. http://mc-stan.org (2018)

  38. Svetina, D., Valdivia, A., Underhill, S., Dai, S., Wang, X.: Parameter recovery in multidimensional item response theory models under complexity and nonnormality. Appl. Psychol. Meas. 41(7), 530–544 (2017)

    Article  Google Scholar 

  39. Tavakol, M., Pinner, G.: Using the many-facet Rasch model to analyse and evaluate the quality of objective structured clinical examination: a non-experimental cross-sectional design. BMJ Open 9(9), 1–9 (2019)

    Article  Google Scholar 

  40. Uto, M.: Accuracy of performance-test linking based on a many-facet Rasch model. Behavior Research Methods p. In press (2020)

    Google Scholar 

  41. Uto, M., Duc Thien, N., Ueno, M.: Group optimization to maximize peer assessment accuracy using item response theory and integer programming. IEEE Trans. Learn. Technol. 13(1), 91–106 (2020)

    Article  Google Scholar 

  42. Uto, M., Okano, M.: Robust neural automated essay scoring using item response theory. In: Proceedings of the International Conference on Artificial Intelligence in Education, pp. 549–561 (2020)

    Google Scholar 

  43. Uto, M., Ueno, M.: Item response theory for peer assessment. IEEE Trans. Learn. Technol. 9(2), 157–170 (2016)

    Article  Google Scholar 

  44. Uto, M., Ueno, M.: Empirical comparison of item response theory models with rater’s parameters. Heliyon 4(5), 1–32 (2018)

    Article  Google Scholar 

  45. Uto, M., Ueno, M.: Item response theory without restriction of equal interval scale for rater’s score. In: Proceedings of the International Conference on Artificial Intelligence in Education, pp. 363–368 (2018)

    Google Scholar 

  46. Uto, M., Ueno, M.: A generalized many-facet Rasch model and its Bayesian estimation using Hamiltonian Monte Carlo. Behaviormetrika 47(2), 469–496 (2020)

    Article  Google Scholar 

  47. Watanabe, S.: Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. J. Mach. Learn. Res. 11(12), 3571–3594 (2010)

    Google Scholar 

  48. Wilson, M., Hoskens, M.: The rater bundle model. J. Educ. Behav. Stat. 26(3), 283–306 (2001)

    Article  Google Scholar 

  49. Wind, S.A., Jones, E.: The effects of incomplete rating designs in combination with rater effects. J. Educ. Meas. 56(1), 76–100 (2019)

    Article  Google Scholar 

  50. Yao, L., Schwarz, R.D.: A multidimensional partial credit model with associated item and test statistics: an application to mixed-format tests. Appl. Psychol. Meas. 30(6), 469–492 (2006)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. The University of Electro-Communications, Tokyo, Japan

    Masaki Uto

Authors
  1. Masaki Uto
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Masaki Uto .

Editor information

Editors and Affiliations

  1. Technion – Israel Institute of Technology, Haifa, Israel

    Ido Roll

  2. Arizona State University, Tempe, AZ, USA

    Danielle McNamara

  3. Utrecht University, Utrecht, The Netherlands

    Sergey Sosnovsky

  4. London Knowledge Lab, London, UK

    Rose Luckin

  5. University of Leeds, Leeds, UK

    Vania Dimitrova

Rights and permissions

Reprints and permissions

Copyright information

© 2021 Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Uto, M. (2021). A Multidimensional Item Response Theory Model for Rubric-Based Writing Assessment. In: Roll, I., McNamara, D., Sosnovsky, S., Luckin, R., Dimitrova, V. (eds) Artificial Intelligence in Education. AIED 2021. Lecture Notes in Computer Science(), vol 12748. Springer, Cham. https://doi.org/10.1007/978-3-030-78292-4_34

Download citation

  • DOI: https://doi.org/10.1007/978-3-030-78292-4_34

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-030-78291-7

  • Online ISBN: 978-3-030-78292-4

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics