Abstract
We describe subquadratic algorithms, in the algebraic decision-tree model of computation, for detecting whether there exists a triple of points, belonging to three respective sets A, B, and C of points in the plane, that satisfy a pair of polynomial equations. In particular, this has an application to detect collinearity among three sets A, B, C of n points each, in the complex plane, when each of the sets A, B, C lies on some constant-degree algebraic curve. In another development, we present a subquadratic algorithm, in the algebraic decision-tree model, for the following problem: Given a pair of sets A, B each consisting of n pairwise disjoint line segments in the plane, and a third set C of arbitrary line segments in the plane, determine whether \(A\times B\times C\) contains a triple of concurrent segments. This is one of four 3sum-hard geometric problems recently studied by Chan (2020). The results reported in this extended abstract are based on the recent studies of the author with Aronov and Sharir (2020, 2021).
Work partially supported by NSF CAREER under grant CCF:AF-1553354 and by Grant 824/17 from the Israel Science Foundation.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
The work in [5] also shows how to detect whether A, B, C satisfy a single polynomial equation under the condition that two of the sets lie on two respective one-dimensional curves and the third is placed arbitrarily in the plane. We do not report this particular development in this extended abstract.
- 2.
A two-dimensional algebraic surface S in \({\mathbb {R}}^4\) has good fibers if, for every point \(p \in {\mathbb {R}}^2\), the fibers \((\{p\} \times {\mathbb {R}}^2) \cap S\) and \(({\mathbb {R}^2} \times \{p\}) \cap S\) are finite.
- 3.
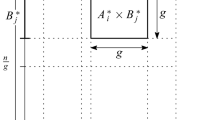
The number of cells is in fact \(O(n/g)^2)\), but the analysis in [5] uses hierarchical polynomial partitioning in order to speed up computation, which slightly increases the number of cells to \(O((n/g)^{2 + \varepsilon })\). We skip this variant in this extended abstract.
References
Agarwal, P.K.: Simplex range searching and its variants: a review. In: Loebl, M., Nešetřil, J., Thomas, R. (eds.) A Journey Through Discrete Mathematics, pp. 1–30. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-44479-6_1
Agarwal, P.K., Aronov, B., Ezra, E., Zahl, J.: An efficient algorithm for generalized polynomial partitioning and its applications. In: Proceedings of 35th Symposium on Computational Geometry, pp. 5:1–5:14 (2020). arXiv:1812.10269
Agarwal, P.K., Matoušek, J., Sharir, M.: On range searching with semialgebraic sets II. SIAM J. Comput. 42, 2039–2062 (2013)
Ailon, N., Chazelle, B.: Lower bounds for linear degeneracy testing. J. ACM 52(2), 157–171 (2005)
Aronov, B., Ezra, E., Sharir, M.: Testing polynomials for vanishing on Cartesian products of planar point sets, In: Proceedings of 36th Symposium on Computational Geometry, pp. 8:1–8:14 (2020). arXiv:2003.09533
Aronov, B., Ezra, E., Sharir, M.: Subquadratic algorithms for some 3SUM-Hard geometric problems in the algebraic decision-tree model, Manuscript (2021)
Barba, L., Cardinal, J., Iacono, J., Langerman, S., Ooms, A., Solomon, N.: Subquadratic algorithms for algebraic 3SUM, Discrete Comput. Geom. 61, 698–734 (2019). Also in Proceedings 33rd International Symposium on Computational Geometry, pp. 13:1–13:15 (2017)
Cardinal, J., Iacono, J., Ooms, A.: Solving \(k\)-SUM using few linear queries, In: Proceedings of 24th European Symposium on Algorithms, pp. 25:1–25:17 (2016)
Chan, T.M.: More logarithmic-factor speedups for 3SUM, (median,\(+\))-convolution, and some geometric 3SUM-hard problems, ACM Trans. Algorithms 16, 7:1–7:23 (2020)
de Berg, M., Schwarzkopf, O.: Cuttings and applications. Int. J. Comput. Geometry Appl. 5, 343–355 (1995)
Erickson, J.: Lower bounds for linear satisfiability problems. Chicago. J. Theoret. Comput. Sci. 8, 388–395 (1997)
Erickson, J., Seidel, R.: Better lower bounds on detecting affine and spherical degeneracies. Discrete Comput. Geom. 13(1), 41–57 (1995). https://doi.org/10.1007/BF02574027
Ezra, E., Har-Peled, S., Kaplan, H., Sharir, M.: Decomposing arrangements of hyperplanes: VC-dimension, combinatorial dimension, and point location. Discrete Comput. Geom 64(1), 109–173 (2020)
Ezra, E., Sharir, M.: A nearly quadratic bound for point-location in hyperplane arrangements, in the linear decision tree model. Discrete Comput. Geom. 61(4), 735–755 (2018). https://doi.org/10.1007/s00454-018-0043-8
Gajentaan, A., Overmars, M.H.: On a class of \({O}(n^2)\) problems in computational geometry. Comput. Geom. Theory Appl. 5, 165–185 (1995)
Grønlund, A., Pettie, S.: Threesomes, degenerates, and love triangles, J. ACM 65 22:1–22:25 (2018). Also in Proceedings of 55th Annul Symposium on Foundations of of Computer Science, pp. 621–630 (2014)
Guth, L., Katz, N.H.: On the Erdős distinct distances problem in the plane, Annals Math. 181, 155–190 (2015). arXiv:1011.4105
Hopkins, M., Kane, D.M., Lovett, S., Mahajan, G.: Point location and active learning: learning halfspaces almost optimally. In: Proceedings of 61st IEEE Annual Symposium on Foundations of Computer Science, (FOCS) (2020)
Kane, D.M., Lovett, S., Moran, S.: Near-optimal linear decision trees for k-SUM and related problems, J. ACM 66, 16:1–16:18 (2019). Also in Proceedings of 50th Annul ACM Symposium on Theory Computational, pp. 554–563 (2018). arXiv:1705.01720
Meiser, S.: Point location in arrangements of hyperplanes. Inf. Comput. 106(2), 286–303 (1993)
Meyer auf der Heide, F.: A polynomial linear search algorithm for the \(n\)-dimensional knapsack problem. J. ACM 31, 668–676 (1984)
Solymosi, J., de Zeeuw, F.: Incidence bounds for complex algebraic curves on cartesian products. In: Ambrus, G., Bárány, I., Böröczky, K.J., Fejes Tóth, G., Pach, J. (eds.) New Trends in Intuitive Geometry. BSMS, vol. 27, pp. 385–405. Springer, Heidelberg (2018). https://doi.org/10.1007/978-3-662-57413-3_16
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Ezra, E. (2021). On 3SUM-hard Problems in the Decision Tree Model. In: De Mol, L., Weiermann, A., Manea, F., Fernández-Duque, D. (eds) Connecting with Computability. CiE 2021. Lecture Notes in Computer Science(), vol 12813. Springer, Cham. https://doi.org/10.1007/978-3-030-80049-9_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-80049-9_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-80048-2
Online ISBN: 978-3-030-80049-9
eBook Packages: Computer ScienceComputer Science (R0)