Abstract
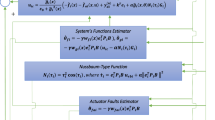
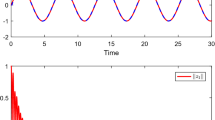
This paper describes a fuzzy logic controller for fault tolerant control of nonlinear flat systems. The control hybridizes flat reference parameters with a fuzzy logic control regulator to achieve robustness against sensing and effector faults for control of a three-tank system. Two methods of fault tolerant control are presented. One method is passive in that although a control reconfiguration is applied, it is not explicitly attached to the detection of any faults and instead applies a general principle to the problem class. This method applies only a fuzzy logic control regulator to a flatness-derived reference signal. The second method is active and applies a control reconfiguration based on the analysis of residuals taken from the difference between the measured signals and the flat system signals. The feasibility of these approaches are verified for additive and multiplicative faults in a three-tank system.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Martinez-Torres, C., Lavigne, L.F., Cazaurang, F., Alcorta-Garcia, E., Diaz-Romero, D.: Flatness-based fault tolerant control. Dyna 81(188), 130–137 (2014)
Isermann, R.: Fault-diagnosis systems: an introduction from fault detection to fault tolerance. Springer (2006). https://doi.org/10.1007/3-540-30368-5
Benosman, M.: Passive fault tolerant control, robust control, Theory and applications (2011). https://www.intechopen.com/books/robust-control-theory-and-applications/passive-fault-tolerant-control. Accessed 1 Jan 2021
Mai, P., Join, C., Reger ,J.: Flatness-based fault tolerant control of a non-linear MIMO system using algebraic derivative estimation. In: 3rd IFAC Symposium on System, Structure and Control, SSC 2007 (2007)
Suryawan, F., De Dona, J., Seron, M.: Fault detection, isolation, and recovery using spline tools and differential flatness with application to a magnetic levitation system. In: Control and Fault Tolerant Systems (SysTol), 2010 Conference on. IEEE, pp. 293–298 (2010)
Charlet, B., Levine, J., Marino, R.: Sufficient conditions for dynamic state feedback linearization. SIAM J. Control. Optim. 29(1), 38–57 (1991)
Martin, P.: Contribution a l’etude des systemes differentiellement. Ph.D. Thesis, Ecole des Mines, Paris, France (1992)
Fliess, M., Levine, J., Martin, P., Rouchon, P.: Flatness and defect of non-linear systems: introductory theory and examples. Int. J. Control 61(6), 1327–1361 (1995)
Noura, H., Theilliol, D., Ponsart, J.C., Chamseddine, A.: Fault-tolerant control systems: design and practical applications. Springer (2009)
Martinez-Torres, C., Lavigne, L.F., Cazaurang, F., Alcorta-Garcia, E., Diaz-Romero, D.: Fault tolerant control of a three tank system: a flatness based approach. In: 2nd International Conference on Control and Fault-Tolerant Systems. Nice, France (2013)
Louembet, C.: Generation de trajectoires optimales pour systemes differentiellement plats: application aux manoeuves d’attitude sur orbite. Universite de Bordeaux, Bordeaux, France. Ph.D. Thesis (2007)
Louembet, C., Cazaurang, F., Zolghadri, A.: Motion planning for flat systems using positive B-splines: an LMI approach. Automatica 46(8), 1305–1309 (2010)
Acknowledgements
The author would like to gratefully acknowledge the IMS Laboratory at the University of Bordeaux in Bordeaux, France, where most of this research was carried out. The author would also like to acknowledge the QtFuzzyLite platform which assisted in the fuzzy visualization presented herein.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Macmann, O., Cohen, K., Cazaurang, F. (2022). Fuzzy-Flatness Hybrid Fault-Tolerant Control. In: Rayz, J., Raskin, V., Dick, S., Kreinovich, V. (eds) Explainable AI and Other Applications of Fuzzy Techniques. NAFIPS 2021. Lecture Notes in Networks and Systems, vol 258. Springer, Cham. https://doi.org/10.1007/978-3-030-82099-2_24
Download citation
DOI: https://doi.org/10.1007/978-3-030-82099-2_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-82098-5
Online ISBN: 978-3-030-82099-2
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)