Skip to main content
Springer Nature Link
Log in

A Population-Based Framework for Solving the Job Shop Scheduling Problem

  • Conference paper
  • First Online:
Computational Collective Intelligence (ICCCI 2021)

Part of the book series: Lecture Notes in Computer Science ((LNAI,volume 12876))

Included in the following conference series:

  • 1494 Accesses

Abstract

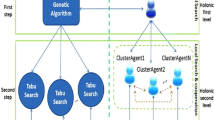
The paper proposes the framework named MPF, extending the Mushroom Picking Metaheuristics and originally proposed earlier by the authors. The framework can be used for solving combinatorial optimization problems. In the current study, the framework has been used for solving instances of the Job Shop Scheduling Problem (JSSP). The framework allows defining several solutions improving agents. Agents work in parallel trying to improve solutions. Solutions are maintained on two levels – common memory and sub-populations for each thread. The framework provides functionality allowing the implementation of a strategy for maintenance of threads and the common memory, including the information exchange between them. For the JSSP implementation, we propose 5 types of autonomous agents. The computational experiment carried out using benchmark datasets has confirmed the good performance of the proposed approach in terms of solutions quality and computation times.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Boussaïd, I., Lepagnot, J., Siarry, P.: A survey on optimization metaheuristics. Inf. Sci. 237, 82–117 (2013). https://doi.org/10.1016/j.ins.2013.02.041

    Article  MathSciNet  MATH  Google Scholar 

  2. Chen, X., Zhang, B., Gao, D.: Algorithm based on improved genetic algorithm for job shop scheduling problem, pp. 951–956 (2019). https://doi.org/10.1109/ICMA.2019.8816334

  3. Dabah, A., Bendjoudi, A., AitZai, A., Nouali-Taboudjemat, N.: Efficient parallel tabu search for the blocking job shop scheduling problem. Soft Comput. 23 (2019). https://doi.org/10.1007/s00500-019-03871-1

  4. Hu, H., Lei, W., Gao, X., Zhang, Y.: Job-shop scheduling problem based on improved cuckoo search algorithm. Int. J. Simul. Model. 17, 337–346 (2018). https://doi.org/10.2507/IJSIMM17(2)CO8

    Article  Google Scholar 

  5. Jedrzejowicz, P.: Current trends in the population-based optimization. In: Nguyen, N.T., Chbeir, R., Exposito, E., Aniorté, P., Trawiński, B. (eds.) ICCCI 2019. LNCS (LNAI), vol. 11683, pp. 523–534. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-28377-3_43

    Chapter  Google Scholar 

  6. Jedrzejowicz, P., Wierzbowska, I.: Parallelized swarm intelligence approach for solving TSP and JSSP problems. Algorithms 13(6), 142 (2020). https://doi.org/10.3390/a13060142

    Article  MathSciNet  Google Scholar 

  7. Jedrzejowicz, P., Wierzbowska, I.: The power of a collective: team of agents solving instances of the flow shop and job shop problems. In: Paszynski, M., Kranzlmüller, D., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M.A. (eds.) ICCS 2021. LNCS, vol. 12744, pp. 406–419. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77967-2_34

    Chapter  Google Scholar 

  8. Kalshetty, Y., Adamuthe, A., Kumar, S.: Genetic algorithms with feasible operators for solving job shop scheduling problem. J. Sci. Res. 64, 310–321 (2020). https://doi.org/10.37398/JSR.2020.640157

    Article  Google Scholar 

  9. Kurdi, M.: An effective genetic algorithm with a critical-path-guided giffler and thompson crossover operator for job shop scheduling problem. Int. J. Intell. Syst. Appl. Eng. 7(1), 13–18 (2019). https://doi.org/10.18201/ijisae.2019751247, https://www.ijisae.org/IJISAE/article/view/790

  10. Lenstra, J., Rinnooy Kan, A., Brucker, P.: Complexity of machine scheduling problems. Ann. Discrete Math. 1, 343–362 (1977). https://doi.org/10.1016/S0167-5060(08)70743-X

    Article  MathSciNet  MATH  Google Scholar 

  11. Liu, M., Yao, X., Li, Y.: Hybrid whale optimization algorithm enhanced with lévy flight and differential evolution for job shop scheduling problems. Appl. Soft Comput. 87, 105954 (2020)

    Article  Google Scholar 

  12. Piroozfard, H., Wong, K., Derakhshanasl, A.: A hybrid harmony search algorithm for the job shop scheduling problems, pp. 48–52 (2015). https://doi.org/10.1109/ASEA.2015.23

  13. Pongchairerks, P.: An enhanced two-level metaheuristic algorithm with adaptive hybrid neighborhood structures for the job-shop scheduling problem. Complexity 2020, 1–15 (2020). https://doi.org/10.1155/2020/3489209

    Article  Google Scholar 

  14. Rameshkumar, K., Rajendran, C.: A novel discrete PSO algorithm for solving job shop scheduling problem to minimize makespan. In: IOP Conference Series: Materials Science and Engineering, vol. 310, p. 012143 (2018). https://doi.org/10.1088/1757-899x/310/1/012143

  15. Sun, L., Lin, L., Li, H., Gen, M.: Large scale flexible scheduling optimization by a distributed evolutionary algorithm. Comput. Ind. Eng. 128, 894–904 (2019). https://doi.org/10.1016/j.cie.2018.09.025

    Article  Google Scholar 

  16. Tsai, C.W., Chang, H.C., Hu, K.C., Chiang, M.C.: Parallel coral reef algorithm for solving jsp on spark. In: 2016 IEEE International Conference on Systems, Man, and Cybernetics, SMC 2016, Budapest, Hungary, 9–12 October 2016, pp. 1872–1877. IEEE (2016). https://doi.org/10.1109/SMC.2016.7844511

  17. Çaliş Uslu, B., Bulkan, S.: A research survey: review of ai solution strategies of job shop scheduling problem. J. Intell. Manuf. 26 (2013). https://doi.org/10.1007/s10845-013-0837-8

  18. Viana, M.S., Morandin Junior, O., Contreras, R.C.: A modified genetic algorithm with local search strategies and multi-crossover operator for job shop scheduling problem. Sensors 20(18), 5440 (2020). https://doi.org/10.3390/s20185440

    Article  Google Scholar 

  19. Vital-Soto, A., Azab, A., Baki, M.F.: Mathematical modeling and a hybridized bacterial foraging optimization algorithm for the flexible job-shop scheduling problem with sequencing flexibility. J. Manuf. Syst. 54, 74–93 (2020). https://doi.org/10.1016/j.jmsy.2019.11.010

    Article  Google Scholar 

  20. Wang, F., Tian, Y., Wang, X.: A discrete wolf pack algorithm for job shop scheduling problem. In: Proceedings of the 2019 5th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, pp. 19–22 (2019)

    Google Scholar 

  21. Yamada, T.: Studies on metaheuristics for jobshop and flowshop scheduling problems (2003)

    Google Scholar 

  22. Yu, H., Gao, Y., Wang, L., Meng, J.: A hybrid particle swarm optimization algorithm enhanced with nonlinear inertial weight and gaussian mutation for job shop scheduling problems. Mathematics 8(8) (2020). https://doi.org/10.3390/math8081355, https://www.mdpi.com/2227-7390/8/8/1355

  23. Zhang, Z., Guan, Z., Zhang, J., Xie, X.: A novel job-shop scheduling strategy based on particle swarm optimization and neural network. Int. J. Simul. Model. 18, 699–707 (2019). https://doi.org/10.2507/IJSIMM18(4)CO18

    Article  Google Scholar 

  24. Zhu, J., Shao, Z., Chen, C.: An improved whale optimization algorithm for job-shop scheduling based on quantum computing. Int. J. Simul. Model. 18, 521–530 (2019). https://doi.org/10.2507/IJSIMM18(3)CO13

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Gdynia Maritime University, Gdynia, Poland

    Piotr Jedrzejowicz, Ewa Ratajczak-Ropel & Izabela Wierzbowska

Authors
  1. Piotr Jedrzejowicz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ewa Ratajczak-Ropel
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Izabela Wierzbowska
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Izabela Wierzbowska .

Editor information

Editors and Affiliations

  1. Wrocław University of Science and Technology, Wrocław, Poland

    Ngoc Thanh Nguyen

  2. Democritus University of Thrace, Kimmeria, Xanthi, Greece

    Lazaros Iliadis

  3. University of Piraeus, Piraeus, Greece

    Ilias Maglogiannis

  4. Wrocław University of Science and Technology, Wrocław, Poland

    Bogdan Trawiński

Rights and permissions

Reprints and permissions

Copyright information

© 2021 Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Jedrzejowicz, P., Ratajczak-Ropel, E., Wierzbowska, I. (2021). A Population-Based Framework for Solving the Job Shop Scheduling Problem. In: Nguyen, N.T., Iliadis, L., Maglogiannis, I., Trawiński, B. (eds) Computational Collective Intelligence. ICCCI 2021. Lecture Notes in Computer Science(), vol 12876. Springer, Cham. https://doi.org/10.1007/978-3-030-88081-1_26

Download citation

  • DOI: https://doi.org/10.1007/978-3-030-88081-1_26

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-030-88080-4

  • Online ISBN: 978-3-030-88081-1

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics