Abstract
Flexible programming languages with built-in bounds on time or space resources are of obvious practical interest. Since we know that no programming language can capture exactly the PTime (or PSpace) algorithms, the challenge is to design languages that guarantee PTime while accommodating a broad spectrum of algorithmic methods. We propose here such languages for PTime and PSpace, based on size-sensitive imperative programming, parameterless procedures, and a retooling of the ramification method.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Unlike the traditional notion of structure expansion, here
 may have a larger universe than
may have a larger universe than
 .
. - 2.
A common alternative notation is
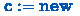 .
. - 3.
 memorizes the atom denoted by
memorizes the atom denoted by
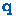 , in case the contraction renders that atom inaccessible.
, in case the contraction renders that atom inaccessible. - 4.
Recall that our vocabularies are lists.
- 5.
 d
d
 need not be disjoint, and
need not be disjoint, and
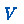 need not be their union.
need not be their union. - 6.
See Definition 3.
- 7.
These successor and predecessor programs are in constant time, in contrast to the linear time obtained when acting on the final atom of the input.
- 8.
Leaving some ids unranked is akin to assigning them 0.
- 9.
I.e. ramified recurrence over strings “with parameter substitution".
- 10.
I.e. defined without subtraction or negative integers.
References
Aehlig, K., Berger, U., Hofmann, M., Schwichtenberg, H.: An arithmetic for non-size-increasing polynomial-time computation. TCS 318(1–2), 3–27 (2004)
Bellantoni, S.: Predicative recursion and computational complexity. Ph.D. thesis, University of Toronto (1992)
Bellantoni, S.: Predicative recursion and the polytime hierarchy. In: Clote, P., Remmel, J. (eds.) Feasible Mathematics II, pp. 15–29. Birkhäuser (1994)
Bellantoni, S., Cook, S.A.: A new recursion-theoretic characterization of the polytime functions. Comput. Complex. 2, 97–110 (1992). https://doi.org/10.1007/BF01201998
Ben-Amram, A.M.: On decidable growth-rate properties of imperative programs. In: Baillot, P. (eds.) International Workshop on Developments in Implicit Computational Complexity. EPTCS, vol. 23, pp. 1–14 (2010)
Ben-Amram, A.M., Hamilton, G.W.: Tight worst-case bounds for polynomial loop programs. In: Bojańczyk, M., Simpson, A. (eds.) FoSSaCS 2019. LNCS, vol. 11425, pp. 80–97. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17127-8_5
Ben-Amram, A.M., Jones, N.D., Kristiansen, L.: Linear, polynomial or exponential? complexity inference in polynomial time. In: Beckmann, A., Dimitracopoulos, C., Löwe, B. (eds.) CiE 2008. LNCS, vol. 5028, pp. 67–76. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-69407-6_7
Bernays, P.: A system of axiomatic set theory - part I. JSL 2, 65–77 (1937)
Bloch, S.A.: Functional characterizations of uniform log-depth and polylog-depth circuit families. In: Proceedings, Structure in Complexity Theory, pp. 193–206. IEEE Computer Society (1992)
Böhm, C., Berarducci, A.: Automatic synthesis of typed lambda-programs on term algebras. Theor. Comput. Sci. 39, 135–154 (1985)
Cobham, A.: The intrinsic computational difficulty of functions. In: Bar-Hillel, Y. (ed.) Proceedings of the International Conference on Logic, Methodology, and Philosophy of Science, North-Holland, Amsterdam, pp. 24–30 (1962)
Constable, R.: Type two computational complexity. In: Proceedings of the Fifth ACM Symposium on Theory of Computing, pp. 108–121 (1973)
Dijkstra, E.W.: A Discipline of Programming. Prentice-Hall, Hoboken (1976)
Gries, D.: The Science of Programming. Springer, Heidelberg (1981). https://doi.org/10.1007/978-1-4612-5983-1
Hájek, P.: Arithmetical hierarchy and complexity of computation. Theoret. Comput. Sci. 8, 227–237 (1979)
Handley, W.G.: Bellantoni and Cook’s characterization of polynomial time functions. Typescript, August 1992
Harel, D., Kozen, D., Tiuryn, J.: Dynamic Logic. MIT Press, Cambridge (2000)
Hofmann, M.: Type systems for polynomial-time computation. Ph.D. thesis, Universitat Darmstadt (1998)
Hofmann, M.: Linear types and non-size-increasing polynomial time computation. Inf. Comput. 183(1), 57–85 (2003)
Kanamori, A.: Bernays and set theory. Bull. Symb. Logic 15(1), 43–69 (2009)
Kristiansen, L.: The implicit computational complexity of imperative programming languages. Technical report, BRICS (2001)
Kristiansen, L., Niggl, K.-H.: On the computational complexity of imperative programming languages. Theor. Comput. Sci. 318(1–2), 139–161 (2004)
Lago, U.D., Toldin, P.P.: A higher-order characterization of probabilistic polynomial time. Inf. Comput. 241, 114–141 (2015)
Leivant, D.: Stratified functional programs and computational complexity. In: Twentieth Annual ACM Symposium on Principles of Programming Languages, New York, pp. 325–333. ACM (1993)
Leivant, D.: Predicative recurrence in finite types. In: Nerode, A., Matiyasevich, Y.V. (eds.) LFCS 1994. LNCS, vol. 813, pp. 227–239. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58140-5_23
Leivant, B.: Ramified recurrence and computational complexity i: word recurrence and poly-time. In: Feasible Mathematics II, New York, pp. 320–343. Birkhauser-Boston (1994)
Leivant, D.: Ramified recurrence and computational complexity I: word recurrence and poly-time. In: Clote, P., Remmel, J. (eds.) Feasible Mathematics II, Perspectives in Computer Science, pp. 320–343. Birkhauser-Boston, New York (1994). www.cs.indiana.edu/~leivant/papers
Leivant, D.: A characterization of NC by tree recurrence. In: Thirty Ninth FOCS, pp. 716–724. IEEE Computer Society (1998)
Leivant, D.: A theory of finite structures. CoRR, abs/1808.04949 (2018)
Leivant, D., Marion, J.-Y.: Ramified recurrence and computational complexity II: substitution and poly-space. In: Pacholski, L., Tiuryn, J. (eds.) CSL 1994. LNCS, vol. 933, pp. 486–500. Springer, Heidelberg (1995). https://doi.org/10.1007/BFb0022277
Leivant, D., Marion, J.-Y.: A characterization of alternating log time by ramified recurrence. Theor. Comput. Sci. 236(1–2), 193–208 (2000)
Leivant, D., Marion, J.-Y.: Evolving graph-structures and their implicit computational complexity. In: ICALP, vol. 40, pp. 349–360 (2013)
Leivant, D., Marion, J.-Y.: Implicit complexity via structure transformation. CoRR, abs/1802.03115 (2018)
Leivant, D., Marion, J.-Y.: Primitive recursion in the abstract. Math. Struct. Comput. Sci. 30(1), 33–43 (2019)
Marion, J.-Y.: A type system for complexity flow analysis. In: Proceedings of the 26th Annual IEEE Symposium on Logic in Computer Science, pp. 123–132 (2011)
Meyer, A., Ritchie, D.: The complexity of loop programs. In: Proceedings of the 1967 22nd National Conference, New York, NY, USA, pp. 465–469. ACM (1967)
Niggl, K.-H., Wunderlich, H.: Certifying polynomial time and linear/polynomial space for imperative programs. SIAM J. Comput. 35(5), 1122–1147 (2006)
Niggl, K.-H., Wunderlich, H.: Implicit characterizations of FPTIME and NC revisited. J. Log. Algebraic Methods Program. 79(1), 47–60 (2010)
Oitavem, I.: Characterizing nc with tier 0 pointers. Math. Log. Q. 50(1), 9–17 (2004)
Oitavem, I.: Characterizing PSPACE with pointers. Math. Log. Q. 54(3), 323–329 (2008)
Oitavem, I.: A recursion-theoretic approach to NP. Ann. Pure Appl. Logic 162(8), 661–666 (2011)
Ritchie, R.W.: Classes of predictably computable functions. Trans. AMS 106, 139–173 (1963)
Schütte, K.: Proof Theory. Springer, Berlin (1977). https://doi.org/10.1007/978-3-642-66473-1
Whitehead, A.N., Russell, B.: Principia Mathematica, vol. II. Cambridge University Press, Cambridge (1912)
Winskel, G.: The Formal Semantics of Programming Languages: An Introduction. MIT Press, Cambridge (1993)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Leivant, D. (2021). Algorithmically Broad Languages for Polynomial Time and Space. In: Silva, A., Wassermann, R., de Queiroz, R. (eds) Logic, Language, Information, and Computation. WoLLIC 2021. Lecture Notes in Computer Science(), vol 13038. Springer, Cham. https://doi.org/10.1007/978-3-030-88853-4_23
Download citation
DOI: https://doi.org/10.1007/978-3-030-88853-4_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-88852-7
Online ISBN: 978-3-030-88853-4
eBook Packages: Computer ScienceComputer Science (R0)


 may have a larger universe than
may have a larger universe than
 .
.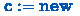 .
. memorizes the atom denoted by
memorizes the atom denoted by
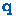 , in case the contraction renders that atom inaccessible.
, in case the contraction renders that atom inaccessible. d
d
 need not be disjoint, and
need not be disjoint, and
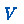 need not be their union.
need not be their union.