Abstract
In computer graphics, animation compression is essential for efficient storage, streaming and reproduction of animated meshes. Previous work has presented efficient techniques for compression by deriving skinning transformations and weights using clustering of vertices based on geometric features of vertices over time. In this work we present a novel approach that assigns vertices to bone-influenced clusters and derives weights using deep learning through a training set that consists of pairs of vertex trajectories (temporal vertex sequences) and the corresponding weights drawn from fully rigged animated characters. The approximation error of the resulting linear blend skinning scheme is significantly lower than the error of competent previous methods by producing at the same time a minimal number of bones. Furthermore, the optimal set of transformation and vertices is derived in fewer iterations due to the better initial positioning in the multidimensional variable space. Our method requires no parameters to be determined or tuned by the user during the entire process of compressing a mesh animation sequence.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Source code available here: https://github.com/AnastasiaMoutafidou/DeepSkinning.
References
Alexa, M., Müller, W.: Representing animations by principal components. Comput. Graph. Forum 19, 411–418 (2000)
Au, O.K.C., Tai, C.L., Chu, H.K., Cohen-Or, D., Lee, T.Y.: Skeleton extraction by mesh contraction. ACM Trans. Graph. 27(3), 44:1–44:10 (2008)
Avril, Q., et al.: Animation setup transfer for 3D characters. In: Proceedings of the 37th Annual Conference of the European Association for Computer Graphics, EG ’16, pp. 115–126. Eurographics Association, Goslar (2016)
Bailey, S.W., Otte, D., Dilorenzo, P., O’Brien, J.F.: Fast and deep deformation approximations. ACM Trans. Graph. 37(4), 1–12 (2018)
De Aguiar, E., Theobalt, C., Thrun, S., Seidel, H.P.: Automatic conversion of mesh animations into skeleton-based animations. Comput. Graph. Forum 27(2), 389–397 (2008)
De Aguiar, E., Theobalt, C., Thrun, S., Seidel, H.P.: Automatic conversion of mesh animations into skeleton-based animations. Comput. Graph. Forum 27, 389–397 (2008)
Feng, A., Casas, D., Shapiro, A.: Avatar reshaping and automatic rigging using a deformable model. In: Proceedings of the 8th ACM SIGGRAPH Conference on Motion in Games, MIG ’15, pp. 57–64. Association for Computing Machinery, New York (2015). https://doi.org/10.1145/2822013.2822017
Hasler, N., Thormählen, T., Rosenhahn, B., Seidel, H.P.: Learning skeletons for shape and pose. In: Proceedings of the 2010 ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games, I3D ’10, pp. 23–30. Association for Computing Machinery, New York (2010). https://doi.org/10.1145/1730804.1730809
Hochreiter, S., Schmidhuber, J.: Long short-term memory. Neural Comput. 9(8), 1735–1780 (1997)
Jacobson, A., Deng, Z., Kavan, L., Lewis, J.P.: Skinning: real-time shape deformation. In: ACM SIGGRAPH 2014 Courses, SIGGRAPH ’14. Association for Computing Machinery, New York (2014). https://doi.org/10.1145/2614028.2615427
James, D.L., Twigg, C.D.: Skinning mesh animations. In: ACM SIGGRAPH 2005 Papers, SIGGRAPH ’05, pp. 399–407. Association for Computing Machinery, New York (2005)
Kavan, L., Collins, S., Žára, J., O’Sullivan, C.: Skinning with dual quaternions. In: Proceedings of the 2007 Symposium on Interactive 3D Graphics and Games, I3D ’07, pp. 39–46. Association for Computing Machinery, New York (2007). https://doi.org/10.1145/1230100.1230107
Kavan, L., McDonnell, R., Dobbyn, S., Žára, J., O’Sullivan, C.: Skinning arbitrary deformations. In: Proceedings of the 2007 Symposium on Interactive 3D Graphics and Games, I3D ’07, pp. 53–60. Association for Computing Machinery, New York (2007)
Kavan, L., Sloan, P.P., O’Sullivan, C.: Fast and efficient skinning of animated meshes. Comput. Graph. Forum 29, 327–366 (2010)
Khan, A., Sohail, A., Zahoora, U., Qureshi, A.S.: A survey of the recent architectures of deep convolutional neural networks (2019)
Kingma, D.P., Ba, J.: Adam: a method for stochastic optimization (2014)
Kraevoy, V., Sheffer, A.: Cross-parameterization and compatible remeshing of 3d models. In: ACM SIGGRAPH 2004 Papers, SIGGRAPH ’04, pp. 861–869. ACM, New York (2004)
Kry, P.G., James, D.L., Pai, D.K.: Eigenskin: real time large deformation character skinning in hardware. In: Proceedings of the 2002 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, SCA ’02, pp. 153–159. Association for Computing Machinery, New York (2002)
Le, B.H., Deng, Z.: Smooth skinning decomposition with rigid bones. ACM Trans. Graph. 31(6), 199:1–199:10 (2012)
Le, B.H., Deng, Z.: Smooth skinning decomposition with rigid bones. ACM Trans. Graph. 31(6) (2012). https://doi.org/10.1145/2366145.2366218
Le, B.H., Deng, Z.: Robust and accurate skeletal rigging from mesh sequences. ACM Trans. Graph. 33(4) (2014). https://doi.org/10.1145/2601097.2601161
Liu, L., Zheng, Y., Tang, D., Yuan, Y., Fan, C., Zhou, K.: Neuroskinning: automatic skin binding for production characters with deep graph networks. ACM Trans. Graph. 38(4), 1–12 (2019)
Luo, R., et al.: Nnwarp: neural network-based nonlinear deformation. IEEE Trans. Vis. Comput. Graph. 26(4), 1745–1759 (2020)
Magnenat-Thalmann, N., Laperrière, R., Thalmann, D.: Joint-dependent local deformations for hand animation and object grasping. In: Proceedings on Graphics Interface ’88, pp. 26–33. Canadian Information Processing Society, CAN (1989)
Mikhailov, A.: Turbo, An Improved Rainbow Colormap for Visualization, Google AI Blog (2019)
Sattler, M., Sarlette, R., Klein, R.: Simple and efficient compression of animation sequences. In: Proceedings of the 2005 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, SCA ’05, pp. 209–217. Association for Computing Machinery, New York (2005)
Schaefer, S., Yuksel, C.: Example-based skeleton extraction. In: Proceedings of the Fifth Eurographics Symposium on Geometry Processing, SGP ’07, pp. 153–162. Eurographics Association, Goslar (2007)
Vasilakis, A.A., Fudos, I., Antonopoulos, G.: Pps: pose-to-pose skinning of animated meshes. In: Proceedings of the 33rd Computer Graphics International, CGI ’16, pp. 53–56. ACM, New York (2016)
Xu, Z., Zhou, Y., Kalogerakis, E., Landreth, C., Singh, K.: RigNet: neural rigging for articulated characters. ACM Trans. Graphi. 39(4), article no. 58, 58:1–58:14 (2020)
Zell, E., Botsch, M.: Elastiface: matching and blending textured faces. In: Proceedings of the Symposium on Non-Photorealistic Animation and Rendering, NPAR ’13, pp. 15–24. ACM, New York (2013)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
1 Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary material 1 (mp4 15672 KB)
Appendices
A Appendix A
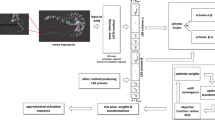
We build an appropriate neural network model that classifies each vertex by capturing mesh geometry and vertex kinematics. Then we use a set of human and animal animations to train the neural network model. We achieve this by using as input features the trajectories of all vertices and as output the weights that represent how each vertex is influenced by a bone. The output weight is conceived by the network as the probability of a bone to influence the corresponding vertex. Subsequently, we provide as input to our network arbitrary mesh animation sequences and predict their weights. From the per vertex classifier we determine the number of bones and the weights for each vertex.
The first error measure is the percentage of deformation known as distortion percentage (DisPer).
where \(\Vert \cdot \Vert _F\) is the Frobenius matrix metric. In Eq. 3 \(A_{orig}\) is a 3NP matrix which consists of the real vertex coordinates in all frames of the model. Similarly, \(A_{Approx}\) has all the approximated vertex coordinates and matrix \(A_{avg}\) contains in each column, the average of the original coordinates in all frames. [14] replaces 100 by 1000 and divides by the surrounding sphere diameter. Sometimes this measure tends to be sensitive to the translation of the entire character, therefore we use a different measure that is invariant to translation. The root mean square (ERMS) error measure in Eq. 4 is an alternative way to express distortion with the difference that we use \(\sqrt{3NP}\) in the denominator so as to obtain the average deformation per vertex and frame during the sequence. \(3NP\) is the total number of elements in the \(A_{orig}\) matrix. [21] uses as denominator the diameter of the bounding box multiplied by \(\sqrt{NP}\).
Max distance denotes the largest vertex error in every frame. So this measure represents the average of max distances over all frames.
Finally, we introduce an additional measure that characterizes the normal distortion - (NormDistort) and is used to measure the different behavior of two animation sequences during rendering. We compute the average difference between the original and the approximated face normals by the norm of their cross product that equals to the sine of the angle between the two normal vectors. Therefore for a model with F faces and P frames, where \(NV^{i,j}\) is the normal vector of face j at frame i, Eq. 6 computes the normal distortion measure.
B Appendix B
Training time for LSTM & CNN networks (Sect. 3.4).
The first network that we propose as the first step and mean of animation compression is a Recurrent Neural Network (RNN).
The type of RNN network used is a Long Short-term Memory network firstly introduced by [9] (LSTM), which consists of units made up of a cell remembering time inconstant data values, a corresponding forget cell, an input and an output gate being responsible of controlling the flow of data in and out of the remembering component of it Fig. 4. Thus, utilization of many network units for LSTM construction (120 units used) produces a network that is able yo predict weights even for models with a large number of bones. Regarding the activation functions we used (i) an alternative for the activation function (cell and hidden state) by using sigmoid instead of tanh and (ii) the default for the recurrent activation function (for input, forget and output gate) which is sigmoid. The main reason of using the sigmoid function instead of the hyperbolic tangent is that our training procedure involves the network deciding per vertex whether it belongs or not to the influence range of a bone. This results in higher efficacy and additionally makes our model learn more effectively.
The second network that we have used successfully is a feed-forward network called Convolutional Neural Network (CNN) [15] that uses convolutional operations to capture patterns in order to determine classes mainly in image classification problems. CNNs are additionally able to be used in classification of sequence data with quite impressive results. On top of the two convolutional layers utilized, we have also introduced a global max-pooling layer (down-sampling layer) and a simple dense layer so that we have the desirable number of weights for each proxy bone, as it is illustrated in Fig. 5. In the two convolutional layers (Conv1D) used we utilize 8 filters of kernel size 2. The number of filters and kernel size have been determined experimentally. However, CNN with small kernel size is working efficiently and it is a reasonable network option on capturing animation sequences due to its capturing capabilities of almost minor transitions from one frame to the next one which is a consequence of small vertex movements within a two consecutive frames interval Fig. 6.
Convolutional kernel & strides representation given an animation sequence input. Blue is used to highlight the previous step of computations (convolutions of input data with filter) and red the next step. In this manner, a Conv1D layer is capable of capturing vertex trajectories in an animation sequence. (Color figure online)
The last network that we have considered for completeness is a hybrid neural network (Fig. 7) that is a combination of the two aforementioned networks with some modifications. Unfortunately, the hybrid network does not perform equally well as its counterparts but it still derives comparable results.
where y are the real values (1: belongs to a bone or 0: does not) and \(y_{pred}\) are the predicted values. Binary cross-entropy measures how far in average a prediction is from the real value for every class. To this end, we also used binary accuracy which calculates the percentage of matched prediction-label pairs the 0/1 threshold value set to 0.5. What we have inferred by these plots is that for CNN there is no reason to increase the batch-size higher than 4096 owing to the fact that accuracy and loss values tend to be almost identical after increasing batch-size from 2048 samples to 4096. Likewise, for the LSTM case (see Fig. 9) we observe that batch-size 2048 is the best option. From Figs. 8 and 9 we infer that we should use at least 20 epochs for training. After that the improvement of loss and accuracy is negligible but as we observed occasional overfitting is alleviated by increasing further the number of epochs.
C Appendix C
The entire method was developedFootnote 1 using Python and Tensorflow under the Blender 2.79b scripting API. The training part runs on a system with an NVIDIA GeForce RTX 2080Ti GPU with 11 GB GDDR6 RAM. We trained our network models with Adam Optimizer [16], \(learning Rate=0.001\) for 20–100 epochs with \(batchSize=4096\) over a training data-set that incorporates 60 animated character models of different size in terms of number of vertices, animations and frames per animation. We have inferred that 20 epochs are usually enough to have our method converging in terms of the error metrics and most importantly towards an acceptable visual outcome. However to obtain better RMS and distortion errors without over-fitting 100 epochs is a safe choice independently of the training set size. Furthermore, with this choice of batch-size we overcome the over-fitting problem that was apparent by observing the Max Average Distance metric and was manifested by locally distorted meshes.
The rest of our algorithm (prediction and optimization) was developed and ran on a commodity computer equipped with an Intel Core i7-4930K 3.4 GHz processor with 48 Gb under Windows 10 64-bit operating System. In addition, the FESAM algorithm was developed and ran on the same system.
Images for the experiments section.
More specifically, presents a comparison of our method on four benchmark animation sequences, that were not produced by fully animated rigs, with all previous combinations of LBS, quaternion-based and SVD methods. N is the number of Vertices, F is the number of frames and the number in round brackets is the result of the method combined with SVD. Our method derives better results in terms of both error and compression rate as compared to methods I–IV. Method V is only cited for reference since it only obtains compression and is not compatible with any of the standard animation pipelines.
In this case of Table 2 we cite the results from the papers since such methods are difficult to reproduce and this goes beyond the scope of this paper. For two models (horse gallop and samba) we have measured the ERMS error and the compression rate percentage (CRP). Note that the results of [21] were converted to our ERMS metric by multiplying by \(\frac{D}{\sqrt{3}}\), where D is the diagonal of the bounding box of the rest pose.
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Moutafidou, A., Toulatzis, V., Fudos, I. (2021). Temporal Parameter-Free Deep Skinning of Animated Meshes. In: Magnenat-Thalmann, N., et al. Advances in Computer Graphics. CGI 2021. Lecture Notes in Computer Science(), vol 13002. Springer, Cham. https://doi.org/10.1007/978-3-030-89029-2_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-89029-2_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-89028-5
Online ISBN: 978-3-030-89029-2
eBook Packages: Computer ScienceComputer Science (R0)