Abstract
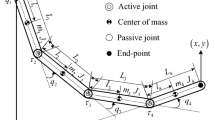
To consider the energy saving during the robot motion, optimal posture control method for a robot manipulator is proposed. The Chebyshev-Gauss (CG) Pseudo-spectral method is used to discuss the problem with the energy optimal control. The Lagrange interpolation of barycentre is adopted to approximate the state and control variables. The continuous optimal control problem can be converted to a discrete nonlinear programming (NLP) problem. And then it can be solved by Sequential Quadratic Programming (SQP) algorithm. The simulation results of optimal energy control make the robot manipulator from the initial state to the desired terminal posture successfully. The terminal angular velocity of each link is also meet the predetermined value. The control law does not exceed the preset boundary of control.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Theodoridis, T., Hu, H.S.: Toward intelligent security robots: a survey. IEEE Trans. Syst. Man. Cy. C. 42(6), 1219–1230 (2012)
Li, C.J., Ma, G.F.: Optimal Control (in Chinese). Science Press, Beijing (2011)
Li, S., Duan, G.R.: Parametric approach to track following control of FFSM. J. Syst. Eng. Electron. 22, 810–815 (2011)
Mostaza-Prieto and P. C. E. Roberts, “Perigee attitude maneuvers of geostationary satellites during Electric orbit raising,” J. Guid. Control. Dynam., 40, 1978–1989, 2017.
Liao, Y.X., Li, H.F., Bao, W.M.: Indirect Radau pseudospectral method for the receding horizon control problem. CHINESE J. Aeronaut. 29, 215–227 (2016)
Yao, Q., Ge, X.: Optimal reorientation of a free-floating space robot subject to initial state uncertainties. J. Braz. Soc. Mech. Sci. Eng. 40(3), 1–12 (2018). https://doi.org/10.1007/s40430-018-1064-1
Tang, X.J., Wei, J.L., Kai, C.: A Chebyshev-Gauss pseudospectral method for solving optimal control problems. ACTA Automatica Sinica. 41, 1778–1787 (2015)
Tang, X.J.: Numerical solution of optimal control problems using multiple-interval integral Gegenbauer pseudospectral methods. ACTA Astronaut. 121, 63–75 (2016)
Ge, X., Yi, Z., Chen, L.: Optimal control of attitude for coupled-rigid-body spacecraft via Chebyshev-Gauss pseudospectral method. Appl. Math. Mech. 38(9), 1257–1272 (2017). https://doi.org/10.1007/s10483-017-2236-8
Arimoto, S.: “Control theory of non-linear mechanical systems: A passivity-based and circuit-theoretic approach. Clarendon Press, Oxford, U.K. (1996)
Lewis, F.L., Dawson, D.M., Abdallah, C.T.: Robot manipulator control: Theory and practice. Marcel Dekker, New York (2004)
Sciavicco, L., Siciliano, B.: Modeling and control of robot manipulators, 2nd edn. Springer-Verlag, London, U.K. (2000)
Su, Y.X., Müller, P.C., Zheng, C.H.: Global asymptotic saturated pid control for robot manipulators. IEEE Trans. Contr. Syst. T. 18(6), 1280–1288 (2010)
Weideman, J., Trefethen, L.: The kink phenomenon in Fejér and Clenshaw-Curtis quadrature. Numer. Math. 107, 707–727 (2007)
Berrut, J.P., Trefethen, L.N.: Barycentric lagrange interpolation. Siam Rev. 46, 501–517 (2004)
Costa, B., Don, W.S.: On the computation of high order pseudo-spectral derivatives. Appl. Numer. Math. 33, 151–159 (2000)
Waldvogel, J.: Fast construction of the Fejér and Clenshaw-Curtis quadrature rules. BIT Numer. Math. 46, 195–202 (2006)
Wang, Y.B., Zhao, Y.M., Bortoff, S.A., Ueda, K.: A real-time energy-optimal trajectory generation method for a servomotor system. IEEE Trans. Ind. Electron. 62(2), 1175–1188 (2015)
Acknowledgement
This research was supported by the National Key R&D Program of China (Grant No. 2019YFB1301403) and National Natural Science Foundation of China (Grant No.62073043). (Corresponding author: Xingguang Duan).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Shi, Q. et al. (2021). Application of CG Pseudo-spectral Method to Optimal Posture Adjustment of Robot Manipulator. In: Liu, XJ., Nie, Z., Yu, J., Xie, F., Song, R. (eds) Intelligent Robotics and Applications. ICIRA 2021. Lecture Notes in Computer Science(), vol 13013. Springer, Cham. https://doi.org/10.1007/978-3-030-89095-7_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-89095-7_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-89094-0
Online ISBN: 978-3-030-89095-7
eBook Packages: Computer ScienceComputer Science (R0)