Abstract
The characterization of the workspace for general spatial 3R chains with skew joint axes is refined by describing the variety of singular displacements as the union of the singular configuration manifolds of orientation type, position type, and attitude type. The surface of attitude singularities is revealed by transferring the singularity sets of spherical 3R chains with intersecting joint axes to the geometry of spatial kinematic chains with skew, non-intersecting joint axes. For this purpose, the degeneracy of a screw system is analyzed by means of a particular angle concept for a set of three oriented lines in space. The obtained argumentation is expressed in terms of geometric manipulator Jacobians completing previous results.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
A sorted pair of two spears
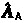 and
and 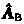 defines a ‘motor’. The special case of intersecting spears with
defines a ‘motor’. The special case of intersecting spears with 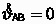 defines a ‘rotor’ and the special case of parallel spears with
defines a ‘rotor’ and the special case of parallel spears with 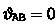 defines a ‘translator’ [25].
defines a ‘translator’ [25]. - 2.
- 3.
- 4.
“Singularities and mobility are characterized by the determinant of the Jacobian matrix for non-redundant manipulators; or by the determinant of the matrix product of the Jacobian and its transpose for redundant mechanisms.” [16].
- 5.
- 6.
Generally it is assumed that only the pair of first axis
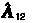 and last axis
and last axis 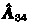 may become coplanar.
may become coplanar.
References
Benoit, R., Delanoue, N., Lagrange, S., Wenger, P.: Guaranteed detection of the singularities of 3R robotic manipulators. In: Flores, P., Viadero, F. (eds.) New Trends in Mechanism and Machine Science. MMS, vol. 24, pp. 69–79. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-09411-3_8
Bohigas, O., Zlatanov, D., Ros, L., Manubens, M., Porta, J.M.: A general method for the numerical computation of manipulator singularity sets. IEEE Trans. Rob. 30(2), 340–351 (2014)
Bongardt, B.: Geometric characterization of the workspace of non-orthogonal rotation axes. J. Geom. Mech. 6, 141 (2014)
Bongardt, B.: Novel Plücker operators and a dual Rodrigues formula applied to the IKP of general 3R chains. In: Lenarcic, J., Parenti-Castelli, V. (eds.) ARK 2018. SPAR, vol. 8, pp. 65–73. Springer, Cham (2019). https://doi.org/10.1007/978-3-319-93188-3_8
Bongardt, B.: The adjoint trigonometric representation of displacements and a closed-form solution to the IKP of general 3C chains. J. Appl. Math. Mech. 100, e201900214 (2020)
Brand, L.: Vector and Tensor Analysis. Wiley, New York (1947)
Burdick, J.W.: A recursive method for finding revolute-jointed manipulator singularities. In: International Conference on Robotics and Automation, vol. 1, pp. 448–453 (1992)
Burdick, J.W.: A classification of 3R regional manipulator singularities and geometries. Mech. Mach. Theory 30(1), 71–89 (1995)
Clifford, W.: A preliminary sketch of biquaternions. Proc. Lond. Math. Soc. 1, 381–395 (1873)
Davidson, J.K., Hunt, K.H., Pennock, G.R.: Robots and Screw Theory: Applications of Kinematics and Statics to Robotics. Oxford University Press, Oxford (2004)
Dimentberg, F.M.: The Screw Calculus and Its Applications to Mechanics. Nauka, Moscow (1965)
Donelan, P.S.: Singularity-theoretic methods in robot kinematics. Robotica 25(06), 641–659 (2007)
Donelan, P.S., Müller, A.: Singularities of regional manipulators revisited. In: Lenarcic, J., Stanisic, M. (eds.) Advances in Robot Kinematics: Motion in Man and Machine. Springer, Dordrecht (2010). https://doi.org/10.1007/978-90-481-9262-5_55
Donelan, P.S., Selig, J.: Hyperbolic pseudoinverses for kinematics in the Euclidean group. SIAM J. Matrix Anal. Appl. 38(4), 1541–1559 (2017)
Fischer, I.S.: Dual-Number Methods in Kinematics, Statics, and Dynamics. CRC Press, Boca Raton (1999)
Chang, K.-S., Khatib, O.: Manipulator control at kinematic singularities: a dynamically consistent strategy. In: International Conference on Intelligent Robots and Systems, vol. 3, pp. 84–88 (1995)
McCarthy, J.M., Soh, G.S.: Geometric Design of Linkages. Springer, New York (2010)
von Mises, R.: Motorrechnung, ein neues Hilfsmittel der Mechanik. ZAMM J. Appl. Math. Mech. Zeitschrift für Angewandte Mathematik und Mechanik 4(2), 155–181 (1924)
Ottaviano, E., Ceccarelli, M., Husty, M.: Workspace topologies of industrial 3R manipulators. Int. J. Adv. Rob. Syst. 4, 38 (2007)
Ottaviano, E., Husty, M., Ceccarelli, M.: Level-set method for workspace analysis of serial manipulators. In: Lennarčič, J., Roth, B. (eds.) Advances in Robot Kinematics, pp. 307–314. Springer, Dordrecht (2006). https://doi.org/10.1007/978-1-4020-4941-5_33
Pai, D.K., Leu, M.C.: Genericity and singularities of robot manipulators. Trans. Robot. Autom. 8(5), 545–595 (1992)
Piovan, G., Bullo, F.: On coordinate-free rotation decomposition: Euler angles about arbitrary axes. Trans. Robot. 28(3), 728–733 (2012)
Pottmann, H., Wallner, J.: Computational Line Geometry. Springer, Heidelberg (2001). https://doi.org/10.1007/978-3-642-04018-4
Selig, J.M.: Geometric Fundamentals of Robotics. Springer, New York (2005). https://doi.org/10.1007/b138859
Strubecker, K.: Studysches Übertragungsprinzip und Motorrechnung. Math. Z. 44(1), 1–19 (1939)
Study, E., : Geometrie der Dynamen: Die Zusammensetzung von Kräften und Verwandte Gegenstände der Geometrie. B. G. Teubner (1903)
Tchoń, K.: Differential topology of the inverse kinematic problem for redundant robot manipulators. Int. J. Robot. Res. 10(5), 492–504 (1991)
Wenger, P.: Cuspidal and noncuspidal robot manipulators. Robotica 25(6), 717–724 (2010)
Yang, A.T., Freudenstein, F.: Application of dual-number quaternion algebra to the analysis of spatial mechanisms. J. Appl. Mech. 31(2), 300–308 (1964)
Yoshikawa, T.: Manipulability of robotic mechanisms. Int. J. Robot. Res. 4(2), 3–9 (1985)
Zlatanov, D., Fenton, R.G., Benhabib, B.: Identification and classification of the singular configurations of mechanisms. In: Computational Kinematics, pp. 163–172 (1995)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Bongardt, B., Müller, A. (2022). On Orientation, Position, and Attitude Singularities of General 3R Chains. In: Holderbaum, W., Selig, J.M. (eds) 2nd IMA Conference on Mathematics of Robotics. IMA 2020. Springer Proceedings in Advanced Robotics, vol 21. Springer, Cham. https://doi.org/10.1007/978-3-030-91352-6_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-91352-6_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-91351-9
Online ISBN: 978-3-030-91352-6
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)


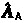 and
and 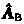 defines a ‘motor’. The special case of intersecting spears with
defines a ‘motor’. The special case of intersecting spears with 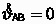 defines a ‘rotor’ and the special case of parallel spears with
defines a ‘rotor’ and the special case of parallel spears with 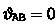 defines a ‘translator’ [
defines a ‘translator’ [ contains so-called ‘dual Plücker coordinates’ [
contains so-called ‘dual Plücker coordinates’ [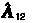 and last axis
and last axis 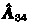 may become coplanar.
may become coplanar.