Abstract
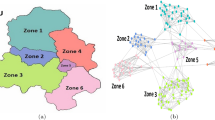
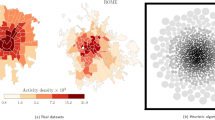
Network–based epidemic models that account for heterogeneous contact patterns are extensively used to predict and control the diffusion of infectious diseases. We use census and survey data to reconstruct a geo–referenced and age–stratified synthetic urban population connected by stable social relations. We consider two kinds of interactions, distinguishing daily (household) contacts from other frequent contacts. Moreover, we allow any couple of individuals to have rare fortuitous interactions. We simulate the epidemic diffusion on a synthetic urban network for a typical medium-sized Italian city and characterize the outbreak speed, pervasiveness, and predictability in terms of the socio–demographic and geographic features of the host population. Introducing age–structured contact patterns results in faster and more pervasive outbreaks, while assuming that the interaction frequency decays with distance has only negligible effects. Preliminary evidence shows the existence of patterns of hierarchical spatial diffusion in urban areas, with two regimes for epidemic spread in low- and high-density regions.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
[23] has no similar condition, but our noise is equivalent to theirs in the limit \(N\rightarrow \infty \).
- 2.
These tests, omitted here due to space limitations, may be made available on request.
References
Kermack, W.O., McKendrick, A.G.: Contributions to the mathematical theory of epidemics-I. Bull. Math. Biol. 53(1–2), 33–55 (1991)
Hethcote, H.W.: The mathematics of infectious diseases. SIAM Rev. 42(4), 599–653 (2000)
Mossong, J., et al.: Social contacts and mixing patterns relevant to the spread of infectious diseases. PLOS Med. 5(3), 1–1 (2008)
Cattuto, C., Van den Broeck, W., Barrat, A., Colizza, V., Pinton, J.-F., Vespignani, A.: Dynamics of person-to-person interactions from distributed RFID sensor networks. PloS one 5(7), e11596 (2010)
Mistry, D., et al.: Inferring high-resolution human mixing patterns for disease modeling (2020). arXiv preprint arXiv:2003.01214
Eubank, S., et al.: Modelling disease outbreaks in realistic urban social networks. Nature 429(6988), 180–184 (2004)
Merler, S., Ajelli, M.: The role of population heterogeneity and human mobility in the spread of pandemic influenza. Proc. Royal Soc. B Biol. Sci. 277(1681), 557–565 (2009)
Chang, S., et al.: Mobility network models of covid-19 explain inequities and inform reopening. Nature 589(7840), 82–87 (2021)
Hufnagel, L., Brockmann, D., Geisel, T.: Forecast and control of epidemics in a globalized world. Proc. Natl. Acad. Sci. 101(42), 15124–15129 (2004)
Colizza, V., Barrat, A., Barthélemy, M., Vespignani, A.: The role of the airline transportation network in the prediction and predictability of global epidemics. Proc. Natl. Acad. Sci. 103(7), 2015–2020 (2006)
Tizzoni, M., et al.: On the use of human mobility proxies for modeling epidemics. PLoS Comput. Biol. 10(7), e1003716 (2014)
Colizza, V., Barrat, A., Barthélemy, M., Vespignani, A.: Predictability and epidemic pathways in global outbreaks of infectious diseases: the SARS case study. BMC Med. 5(1), 1–13 (2007)
Cazelles, B., Champagne, C., Dureau, J.: Accounting for non-stationarity in epidemiology by embedding time-varying parameters in stochastic models. PLoS Comput. Biol. 14(8), e1006211 (2018)
Gupta, S., Anderson, R.M., May, R.M.: Networks of sexual contacts: implications for the pattern of spread of HIV. AIDS (London, England) 3(12), 807–817 (1989)
Newman, M.E.J.: Spread of epidemic disease on networks. Phys. Rev. E 66(1), 016128 (2002)
Keeling, M.J., Eames, K.T.D.: Networks and epidemic models. J. Royal Soc. Interf. 2(4), 295–307 (2005)
Chakrabarti, D., Wang, Y., Wang, C., Leskovec, J., Faloutsos, C.: Epidemic thresholds in real networks. ACM Trans. Inf. Syst. Secur. (TISSEC) 10(4), 1–26 (2008)
Pastor-Satorras, R., Castellano, C., Van Mieghem, P., Vespignani, A.: Epidemic processes in complex networks. Rev. Mod. Phys. 87(3), 925 (2015)
Charu, V., et al.: Human mobility and the spatial transmission of influenza in the united states. PLoS Comput. Biol. 13(2), e1005382 (2017)
Grenfell, B.T., Bjørnstad, O.N., Kappey, J.: Travelling waves and spatial hierarchies in measles epidemics. Nature 414(6865), 716–723 (2001)
Li, R., Richmond, P., Roehner, B.M.: Effect of population density on epidemics. Physica A Stat. Mech. Appl. 510, 713–724 (2018)
Ball, F., Neal, P.: A general model for stochastic sir epidemics with two levels of mixing. Math. Biosci. 180(1–2), 73–102 (2002)
Ball, F., Neal, P.: Network epidemic models with two levels of mixing. Math. Biosci. 212(1), 69–87 (2008)
Kiss, I.Z., Green, D.M., Kao, R.R.: The effect of contact heterogeneity and multiple routes of transmission on final epidemic size. Math. Biosci. 203(1), 124–136 (2006)
Bondarenko, M., Kerr, D., Sorichetta, A., Tatem, A.: Census/projection-disaggregated gridded population datasets for 189 countries in 2020 using built-settlement growth model (bsgm) outputs (2020)
Guarino, S., et al.: Inferring urban social networks from publicly available data. Fut. Internet 13(5), 108 (2021)
Willem, L., Van Hoang, T., Funk, S., Coletti, P., Beutels, P., Hens, N.: SOCRATES: an online tool leveraging a social contact data sharing initiative to assess mitigation strategies for COVID-19. BMC Res. Notes 13(1), 1–8 (2020)
Caldarelli, G., Capocci, A., De Los Rios, P., Muñoz, M.A.: Scale-free networks from varying vertex intrinsic fitness. Phys. Rev. Lett. 89, 258708 (2002)
Guarino, S., et al.: A model for urban social networks. In: Paszynski, M., Kranzlmüller, D., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M.A. (eds.) ICCS 2021. LNCS, vol. 12744, pp. 281–294. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77967-2_23
Biggerstaff, M., Cauchemez, S., Reed, C., Gambhir, M., Finelli, L.: Estimates of the reproduction number for seasonal, pandemic, and zoonotic influenza: a systematic review of the literature. BMC Infect. Dis. 14(1), 1–20 (2014)
Liu, Q.-H., Ajelli, M., Aleta, A., Merler, S., Moreno, Y., Vespignani, A.: Measurability of the epidemic reproduction number in data-driven contact networks. Proc. Natl. Acad. Sci. 115(50), 12680–12685 (2018)
Shu, P., Wang, W., Tang, M., Do, Y.: Numerical identification of epidemic thresholds for susceptible-infected-recovered model on finite-size networks. Chaos Interdisc. J. Nonlinear Sci. 25(6), 063104 (2015)
Medo, M.: Contact network models matching the dynamics of the covid-19 spreading. J. Phys. A Math. Theor. 54(3), 035601 (2020)
Viboud, C., Bjørnstad, O.N., Smith, D.L., Simonsen, L., Miller, M.A., Grenfell, B.T.: Synchrony, waves, and spatial hierarchies in the spread of influenza. Science 312(5772), 447–451 (2006)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Celestini, A., Colaiori, F., Guarino, S., Mastrostefano, E., Zastrow, L.R. (2022). Epidemics in a Synthetic Urban Population with Multiple Levels of Mixing. In: Benito, R.M., Cherifi, C., Cherifi, H., Moro, E., Rocha, L.M., Sales-Pardo, M. (eds) Complex Networks & Their Applications X. COMPLEX NETWORKS 2021. Studies in Computational Intelligence, vol 1073. Springer, Cham. https://doi.org/10.1007/978-3-030-93413-2_27
Download citation
DOI: https://doi.org/10.1007/978-3-030-93413-2_27
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-93412-5
Online ISBN: 978-3-030-93413-2
eBook Packages: EngineeringEngineering (R0)