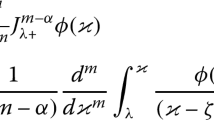Skip to main content
Springer Nature Link
Log in

Constructions of Second Order Approximations of the Caputo Fractional Derivative

  • Conference paper
  • First Online:
Large-Scale Scientific Computing (LSSC 2021)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13127))

Included in the following conference series:

  • 1117 Accesses

Abstract

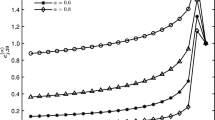
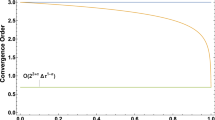
In the present paper we study the properties of the weights of approximations of the second derivative and the Caputo fractional derivative. The approximations of the Caputo derivative are obtained by approximating the second derivative in the expansion formula of the L1 approximation. We show that the properties of their weights are similar to the properties of the weights of the L1 approximation of the Caputo derivative when a suitable choice of the parameters of the approximations is used. The experimental results of applications of the approximations for numerical solution of the two-term ordinary fractional differential equation are given in the paper.

The authors are supported by the Bulgarian National Science Fund under Young Scientists Project KP-06-M32/2 - 17.12.2019. Venelin Todorov is also supported by project No DO1-205/23.11.2018, financed by the Ministry of Education and Science in Bulgaria.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Alikhanov, A.A.: A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 280, 424–438 (2015)

    Article  MathSciNet  Google Scholar 

  2. Batir, N.: Sharp inequalities for factorial n. Proyecciones 27(1), 97–102 (2008)

    MathSciNet  MATH  Google Scholar 

  3. Dimitrov, Y.: A second order approximation for the Caputo fractional derivative. J. Fract. Calc. Appl. 7(2), 175–195 (2016)

    MathSciNet  MATH  Google Scholar 

  4. Dimitrov, Y.: Approximations for the second derivative and the Caputo fractional derivative. In: Proceedings of NSFDE&A 2020, Sozopol, Bulgaria (2020)

    Google Scholar 

  5. Ding, H., Li, C.: High-order numerical algorithms for Riesz derivatives via constructing new generating functions. J. Sci. Comput. 71(2), 759–784 (2017)

    Article  MathSciNet  Google Scholar 

  6. Gao, G.H., Sun, Z.Z., Zhang, H.W.: A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 259, 33–50 (2014)

    Article  MathSciNet  Google Scholar 

  7. Jin, B., Lazarov, R., Zhou, Z.: An analysis of the L1 scheme for the subdiffusion equation with nonsmooth data. IMA J. Numer. Anal. 36(1), 197–221 (2016)

    MathSciNet  MATH  Google Scholar 

  8. Lubich, C.: Discretized fractional calculus. SIAM J. Math. Anal. 17, 704–719 (1986)

    Article  MathSciNet  Google Scholar 

  9. Lin, Y., Xu, C.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225(2), 1533–1552 (2007)

    Article  MathSciNet  Google Scholar 

  10. Tian, W.Y., Zhou, H., Deng, W.H.: A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 84, 1703–1727 (2015)

    Article  MathSciNet  Google Scholar 

  11. Todorov, V., Dimitrov, Y., Dimov, I.: Second order shifted approximations for the first derivative. In: Dimov, I., Fidanova, S. (eds.) HPC 2019. SCI, vol. 902, pp. 428–437. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-55347-0_36

    Chapter  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mathematics and Informatics, Sofia University, 1164, Sofia, Bulgaria

    Stoyan Apostolov

  2. Department of Mathematics and Physics, University of Forestry, 1756, Sofia, Bulgaria

    Yuri Dimitrov

  3. Department of Information Modeling, Institute of Mathematics and Informatics, Bulgarian Academy of Sciences, 1113, Sofia, Bulgaria

    Yuri Dimitrov & Venelin Todorov

  4. Department of Parallel Algorithms, Institute of Information and Communication Technologies, Bulgarian Academy of Sciences, 1113, Sofia, Bulgaria

    Venelin Todorov

Authors
  1. Stoyan Apostolov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuri Dimitrov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Venelin Todorov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yuri Dimitrov .

Editor information

Editors and Affiliations

  1. IICT-BAS, Sofia, Bulgaria

    Ivan Lirkov

  2. IICT-BAS, Sofia, Bulgaria

    Svetozar Margenov

Rights and permissions

Reprints and permissions

Copyright information

© 2022 Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Apostolov, S., Dimitrov, Y., Todorov, V. (2022). Constructions of Second Order Approximations of the Caputo Fractional Derivative. In: Lirkov, I., Margenov, S. (eds) Large-Scale Scientific Computing. LSSC 2021. Lecture Notes in Computer Science, vol 13127. Springer, Cham. https://doi.org/10.1007/978-3-030-97549-4_3

Download citation

  • DOI: https://doi.org/10.1007/978-3-030-97549-4_3

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-030-97548-7

  • Online ISBN: 978-3-030-97549-4

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics