Skip to main content
Springer Nature Link
Log in

Fuzzy Approximate Optimal Solution of the Fuzzy Transportation Problems (FTP) Under Interval Form Using Monte Carlo Approach

  • Conference paper
  • First Online:
Recent Advances in Soft Computing and Data Mining (SCDM 2022)

Part of the book series: Lecture Notes in Networks and Systems ((LNNS,volume 457))

Included in the following conference series:

  • 304 Accesses

Abstract

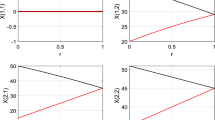
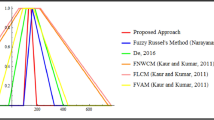
This article presents two phases of procedure to solve the transportation problem under data interval. In the first phase, the problem is transformed into a trapezoidal fuzzy transportation problem by using a trisectional fuzzification. The second phase is to employ the Monte Carlo method based on the alpha-cuts to find the fuzzy optimal solution of the fuzzy transportation problem (FTP). A numerical example is provided to illustrate the capability of the proposed approach and compare it with the existing method. The proposed approach is able to obtain the fuzzy optimal solution of FTP. The computations of the fuzzy optimal solution FTP are conducted by using the Monte Carlo approach by employ random numbers generated by rand(), sort() and reshape() function in the Matlab software. The results indicated that the aforementioned approach can be had a big potential to be further optimized by taking large random numbers.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Kumar, A., Kaur, A.: A new method for solving fuzzy transportation problems using ranking function. Appl. Math. Model. 35, 5652–5661 (2011). https://doi.org/10.1016/j.apm.2011.05.012

    Article  MathSciNet  MATH  Google Scholar 

  2. Kumar, A., Kaur, A.: Application of classical transportation methods for solving fuzzy transportation problems. J. Transp. Syst. Eng. Inf. Technol. 11, 68–80 (2011). https://doi.org/10.1016/S1570-6672(10)60141-9

    Article  MATH  Google Scholar 

  3. Kumar, A., Kaur, A.: A new approach for solving fuzzy transportation problems using generalized trapezoidal fuzzy numbers. Appl. Soft Comp. 12, 1201–1213 (2011). https://doi.org/10.1016/j.asoc.2011.10.014

    Article  Google Scholar 

  4. Ebrahimnejad, A.: A simplified new approach for solving fuzzy transportation problems with generalized trapezoidal fuzzy numbers. Appl. Soft Comp. 19, 171–176 (2014). https://doi.org/10.1016/j.asoc.2014.01.041

    Article  Google Scholar 

  5. Ebrahimnejad, A.: An improved approach for solving fuzzy transportation problem with triangular fuzzy numbers. J. Intell. Fuzzy Syst. 29, 963–974 (2015). https://doi.org/10.3233/IFS-151625

    Article  MathSciNet  MATH  Google Scholar 

  6. Ebrahimnejad, A.: New method for solving fuzzy transportation problems with LR flat fuzzy numbers. Inf. Sci. 357, 108–124 (2016). https://doi.org/10.1016/j.ins.2016.04.008

    Article  MATH  Google Scholar 

  7. Ebrahimnejad, A.: A lexicographic ordering-based approach for solving fuzzy transportation problems with triangular fuzzy numbers. Int. J. Manage. Decis. Making 16, 346–374 (2017). https://doi.org/10.1504/IJMDM.2017.086997

    Article  Google Scholar 

  8. Dasril, Y., Zakaria, Z., Mohd, I.B.: Using alpha-cuts and constraint exploration approach on quadratic programming problem. Telkomnika 16, 2782–2790 (2018). https://doi.org/10.12928/telkomnika.v16i6.11584

  9. Zelibe, S.C., Ugwuanyi, C.P.: On a new solution of the transportation problem. J. Nigerian Math. Soc. 39, 271–291 (2019). ojs.ictp.it/jnms/index.php/jnms/article/view/477

  10. Mathur, N., Srivastava, P.K.: An inventive approach to optimize fuzzy transportation problem. Int. J. Math. Eng. Manage. Sci. 5, 985–994 (2020). https://doi.org/10.33889/IJMEMS.2020.5.5.075

  11. Gurukumaresan, D., Duraisamy, C., Srinivasan, R.: Optimal solution of fuzzy transportation problem using octagonal fuzzy numbers. Comput. Syst. Sci. Eng. 37, 41–421 (2021). https://doi.org/10.32604/csse.2021.014130

    Article  Google Scholar 

  12. Behroozpoor, A.A., Kamyad, A.V., Mazarei, M.M.: Numerical solution of fuzzy initial value problem (FIVP) using optimization. Int. J. Adv. Appl. Sci. 3, 36–42 (2016). https://doi.org/10.21833/ijaas.2016.08.007

  13. Roy, H., Pathak, G., Kumar, R., Malik, Z.A.: A study of fuzzy transportation problem using zero-point method with ranking of trapezoidal fuzzy numbers. Bull. Monumental 12, 24–30 (2020). https://doi.org/10.37896/BMJ21.08/2902

    Article  Google Scholar 

  14. Mathur, N., Srivastava, P.K., Paul, A.: Algorithms for solving fuzzy transportation problem. Int. J. Math. Oper. Res. 12, 190–219 (2018). https://doi.org/10.1504/IJMOR.2018.10010216

  15. Ezzati, R., Khorram, E., Enayati, R.: A new algorithm to solve fully fuzzy linear programming problems using the MOLP problem. Appl. Math. Model. 39, 3183–3193 (2016). https://doi.org/10.1016/j.apm.2013.03.014

    Article  MathSciNet  MATH  Google Scholar 

  16. Chandran, S., Kandaswamy, G.: A fuzzy approach to transport optimization problem. Optim. Eng. 17(4), 965–980 (2012). https://doi.org/10.1007/s11081-012-9202-6

    Article  MathSciNet  MATH  Google Scholar 

  17. Mathur, N., Srivastava, P.K., Paul, A.: Trapezoidal fuzzy model to optimize transportation problem. Int. J. Model. Simul. Sci. Comp. 7, 1–8 (2016). https://doi.org/10.1142/S1793962316500288

  18. Chakraborty, D., Jana, D.K., Roy, T.K.: A new approach to solve fully fuzzy transportation problem using triangular fuzzy number. Int. J. Oper. Res. 26, 153–179 (2016). https://doi.org/10.1504/IJOR.2016.076299

  19. Kumar, R., Edalatpanah, S.A., Jha, S., Singh, R.: A Pythagorean fuzzy approach to the transportation problem. Complex Intell. Syst. 5(2), 255–263 (2019). https://doi.org/10.1007/s40747-019-0108-1

    Article  Google Scholar 

  20. Srivastava, P.K., Bisht, D.C.S.: A segregated advancement in the solution of triangular fuzzy transportation problems. Am. J. Math. Manage. Sci. 40(2), 1–11 (2020). https://doi.org/10.1080/01966324.2020.1854137

  21. Sam’an, M., Farikhin: A new fuzzy transportation algorithm for finding fuzzy optimal solution. Int. J. Math. Model. Num. Opt. 11, 1–19 (2021). https://doi.org/10.1504/IJMMNO.2021.111715

  22. Mhaske, A.S., Bondar, K.L.: Fuzzy transportation by using Monte Carlo method. Adv. Fuzzy Math. 12, 111–127 (2017)

    Google Scholar 

  23. Bisht, D.C.S., Srivastava, P.K.: Trisectional fuzzy trapezoidal approach to optimize interval data-based transportation problem, J. King Saud Univ. Sci. 32, 195–199 (2020). https://doi.org/10.1016/j.jksus.2018.04.013

  24. Fan, M., Zang, Z., Wang, C.: Mathematical Models and Algorithms for Power System Optimization: Modeling Technology for Practical Engineering Problems, 1st Edn. Academic Press, New York (2019)

    Google Scholar 

Download references

Acknowledgment

The authors wish to thank the Research Management Centre (RMC), Universiti Tun Hussein Onn Malaysia, for the support of this research through Research Fund TIER1 no. H777, UTHM.

Author information

Authors and Affiliations

  1. Fuzzy Mathematics and Application Focus Group, Faculty of Technology Management and Business, Universiti Tun Hussein Onn Malaysia, 86400, Batu Pahat, Johor, Malaysia

    Yosza Dasril

  2. Faculty of Technology Management and Business, Universiti Tun Hussein Onn Malaysia, 86400, Batu Pahat, Johor, Malaysia

    Muhammad Sam’an

  3. Informatic, Universitas Muhammadiyah Semarang, Jl. Kedungmundu No. 18, Kedungmundu, Tembalang, Semarang, Central Java, 50273, Indonesia

    Muhammad Sam’an

Authors
  1. Yosza Dasril
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Muhammad Sam’an
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yosza Dasril .

Editor information

Editors and Affiliations

  1. Faculty of Computer Science and Information Technology, Universiti Tun Hussein Onn Malaysia, Batu Pahat, Malaysia

    Rozaida Ghazali

  2. Faculty of Computer Science and Information Technology, Universiti Tun Hussein Onn Malaysia, Batu Pahat, Malaysia

    Nazri Mohd Nawi

  3. Faculty of Computer Science and Information Technology, Universiti Tun Hussein Onn Malaysia, Batu Pahat, Malaysia

    Mustafa Mat Deris

  4. School of Information Technology Faculty of Science, Engineering and Built Environment, Deakin University, Geelong, VIC, Australia

    Jemal H. Abawajy

  5. Faculty of Computer Science and Information Technology, Universiti Tun Hussein Onn Malaysia, Batu Pahat, Malaysia

    Nureize Arbaiy

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Dasril, Y., Sam’an, M. (2022). Fuzzy Approximate Optimal Solution of the Fuzzy Transportation Problems (FTP) Under Interval Form Using Monte Carlo Approach. In: Ghazali, R., Mohd Nawi, N., Deris, M.M., Abawajy, J.H., Arbaiy, N. (eds) Recent Advances in Soft Computing and Data Mining. SCDM 2022. Lecture Notes in Networks and Systems, vol 457. Springer, Cham. https://doi.org/10.1007/978-3-031-00828-3_8

Download citation

Publish with us

Policies and ethics