Graph Coloring and Semidefinite Rank

Abstract

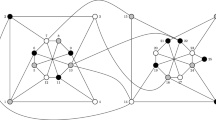
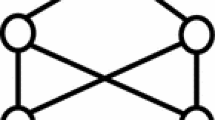
This paper considers the interplay between semidefinite programming, matrix rank, and graph coloring. Karger, Motwani, and Sudan [10] give a vector program for which a coloring of the graph can be encoded as a semidefinite matrix of low rank. By complementary slackness conditions of semidefinite programming, if an optimal dual solution has sufficiently high rank, any optimal primal solution must have low rank. We attempt to characterize graphs for which we can show that the corresponding dual optimal solution must have sufficiently high rank. In the case of the original Karger, Motwani, and Sudan vector program, we show that any graph which is a k-tree has sufficiently high dual rank, and we can extract the coloring from the corresponding low-rank primal solution. We can also show that if the graph is not uniquely colorable, then no sufficiently high rank dual optimal solution can exist. This allows us to completely characterize the planar graphs for which dual optimal solutions have sufficiently high dual rank, since it is known that the uniquely colorable planar graphs are precisely the planar 3-trees.

We then modify the semidefinite program to have an objective function with costs, and explore when we can create a cost function whose optimal dual solution has sufficiently high rank. We show that it is always possible to construct such a cost function given the graph coloring. The construction of the cost function gives rise to a heuristic for graph coloring which we show works well in the case of planar graphs; we enumerated all maximal planar graphs with a $K_4$ of up to 14 vertices, and the heuristics successfully colored 99.75% of them.

Our research was motivated by the Colin de Verdière graph invariant [5] (and a corresponding conjecture of Colin de Verdière), in which matrices that have some similarities to the dual feasible matrices must have high rank in the case that graphs are of a certain type; for instance, planar graphs have rank that would imply the 4-colorability of the primal solution. We explore the connection between the conjecture and the rank of the dual solutions.

Supported by NSF grant CCF-2007009.