Abstract
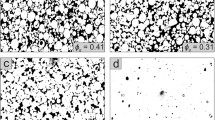
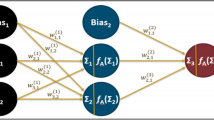
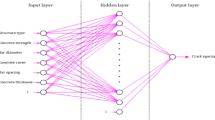
The crack propagation behavior can be considered a time-series forecasting problem and can be observed based on the changes of the Phase-field variable. In this work, we study the behavior of the Isotropic Brittle Fracture Model (BFM), and propose a hybrid computational technique that involves a time-series forecasting method for finding results faster when solving variational equations with a fine-grained. We use this case study to compare and contrast two different time-series forecasting approaches: ARIMA, a statistical method, and LSTM, a neural network learning-based method. The study shows both methods come with different strengths and limitations. However, ARIMA method stands out due to its robustness and flexibility, especially when training data is limited because it can exploit a priori knowledge.
Supported by RMIT University, Vietnam, Internal Research Grant 2, 2020.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Griffith, A.A.: VI. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. London Ser. A 221(582–593), 163–198 (1921)
Moës, N., Dolbow, J., Belytschko, T.: A finite element method for crack growth without remeshing. Int. J. Numer. Meth. Eng. 46(1), 131–150 (1999)
Gardner, E.S., Jr.: Exponential smoothing: the state of the art. J. Forecast. 4, 1–28 (1985)
Yu, Y., Si, X., Hu, C., Zhang, J.: A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 31, 1235–1270 (2019)
Molnár, G., Gravouil, A.: 2D and 3D Abaqus implementation of a robust staggered phase-field solution for modeling brittle fracture. Finite Elem. Anal. Des. 130, 27–38 (2017)
Hamilton, J.D.: Time Series Analysis. Princeton University Press, Princeton (1994)
Dinh, M.N., Vo, C.T., Abramson, D.: Tracking scientific simulation using online time-series modelling. In: 20th IEEE/ACM International Symposium on Cluster, Cloud and Internet Computing, Melbourne, Australia (2020)
Hyndman, R.J., Athanasopoulos, G.: Forecasting: Principles and Practice (2018)
Vo, C.T., Dinh, M.N., Dimla, E.: Predicting phase-field behavior of brittle fracture model based on LSTM time series forecasting model. In: IEEE International Conference on Research, Innovation and Vision for the Future, Ho Chi Minh City, Vietnam (2020)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Dinh, M.N., Vo, C.T., Nguyen, C.T., La, N.M. (2022). Phase-Field Modelling of Brittle Fracture Using Time-Series Forecasting. In: Groen, D., de Mulatier, C., Paszynski, M., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M.A. (eds) Computational Science – ICCS 2022. ICCS 2022. Lecture Notes in Computer Science, vol 13351. Springer, Cham. https://doi.org/10.1007/978-3-031-08754-7_36
Download citation
DOI: https://doi.org/10.1007/978-3-031-08754-7_36
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-08753-0
Online ISBN: 978-3-031-08754-7
eBook Packages: Computer ScienceComputer Science (R0)