Abstract
Error correction is wide and well elaborated area of quantum information theory. Those methods, however, demand additional resources, like quantum gates, qubits or time. We have observed, in statistical sense, that the qubit’s error in real quantum computers, once calibrated doesn’t change much until next one. Then being so, for quantum sampling based computations, one can determine the correction experimentally and use it until the next calibration, without a need of utilize additional resources. In this work we present the method of determining such a correction and applying it to practical quantum-sampling algorithms.
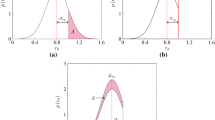
Quantum sampling is the method, which we deliberately decline to obtain one deterministic result of one-shot computation in. Instead of that, we provide a number of same experiments. Then we observe the probability distribution function (PDF) thus obtained, which is considered as the final result of computation. We have observed and experimentally proved in this work, that error of this probability distribution is correlated with the local quantum phase of qubits involved in computations. Hence we are able to create a Phase Distortion Unraveling (PDU) function for each qubit and for whole system as well, that depends on this phase. Briefly, the final result after correction is the sum of PDF and PDU.
This publication was supported by the Department of Graphics, Computer Vision and Digital Systems, under statue research project (Rau6, 2022), Silesian University of Technology (Gliwice, Poland).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
In ideal world we should make statistical analysis what does the word “sufficient” means in the reality, however in real world we are limited to the offer of NISQ computers suppliers. Hence in this work we consider that 8.192 repetitions of the experiment, which is maximal number we can make on IBM Q Experience, is sufficient.
References
Aaronson, S., Gottesman, D.: Improved simulation of stabilizer circuits. Phys. Rev. A 70(5), 052328 (2004). https://doi.org/10.1103/PhysRevA.70.052328, arXiv: quant-ph/0406196
Bravyi, S., Englbrecht, M., König, R., Peard, N.: Correcting coherent errors with surface codes. npj Quantum Inf. 4(1), 55 (2018). https://doi.org/10.1038/s41534-018-0106-y
Dymarsky, A., Shapere, A.: Quantum stabilizer codes, lattices, and CFTs. J. High Energy Phys. 2021(3), 160 (2021). https://doi.org/10.1007/JHEP03(2021)160
Endo, S., Benjamin, S.C., Li, Y.: Practical quantum error mitigation for near-future applications. Phys. Rev. X 8(3), 031027 (2018) https://doi.org/10.1103/PhysRevX.8.031027
Litinski, D.: A game of surface codes: large-scale quantum computing with lattice surgery. Quantum 3, 128 (2019). https://doi.org/10.22331/q-2019-03-05-128
Lv, J., Li, R., Wang, J.: An explicit construction of quantum stabilizer codes from quasi-cyclic codes. IEEE Commun. Lett. 24(5), 1067–1071 (2020) https://doi.org/10.1109/LCOMM.2020.2974731, https://ieeexplore.ieee.org/document/9019839/
Maciejewski, F.B., Zimborás, Z., Oszmaniec, M.: Mitigation of readout noise in near-term quantum devices by classical post-processing based on detector tomography. Quantum 4, 257 (2020). https://doi.org/10.22331/q-2020-04-24-257
Nguyen, D.M., Kim, S.: Quantum stabilizer codes construction from Hermitian self-orthogonal codes over GF(4). J. Commun. Netw. 20(3), 309–315 (2018) https://doi.org/10.1109/JCN.2018.000043, https://ieeexplore.ieee.org/document/8437211/
Nguyen, D.M., Kim, S.: A novel construction for quantum stabilizer codes based on binary formalism. Int. J. Mod. Phys. B 34(08), 2050059 (2020) https://doi.org/10.1142/S0217979220500599
Ryan-Anderson, C., et al.: Realization of real-time fault-tolerant quantum error correction. Phys. Rev. X 11(4), 041058 (2021) https://doi.org/10.1103/PhysRevX.11.041058
Wereszczyński, K., Michalczuk, A., Pęszor, D., Paszkuta, M., Cyran, K., Polański, A.: Cosine series quantum sampling method with applications in signal and image processing. arXiv:2011.12738 [quant-ph], November 2020
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Werner, K., Wereszczyński, K., Michalczuk, A. (2022). Experiment-Driven Quantum Error Reduction. In: Groen, D., de Mulatier, C., Paszynski, M., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M.A. (eds) Computational Science – ICCS 2022. ICCS 2022. Lecture Notes in Computer Science, vol 13353. Springer, Cham. https://doi.org/10.1007/978-3-031-08760-8_17
Download citation
DOI: https://doi.org/10.1007/978-3-031-08760-8_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-08759-2
Online ISBN: 978-3-031-08760-8
eBook Packages: Computer ScienceComputer Science (R0)